关于旋转模型专题

专题01 旋转中的三种全等模型（手拉手、半角、对角互补模型）本专题重点分析旋转中的三类全等模型（手拉手、半角、对角互补模型），结合各类模型展示旋转中的变与不变，并结合经典例题和专项训练深度分析基本图形和归纳主要步骤，同时规范了解题步骤，提高数学的综合解题能力。

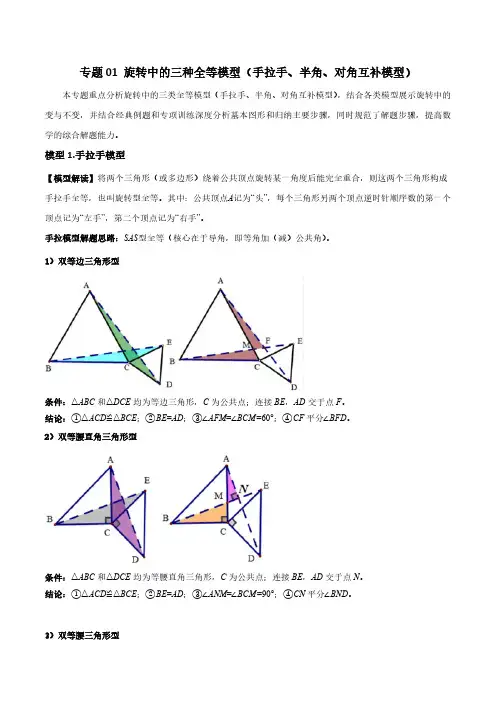
模型1.手拉手模型【模型解读】将两个三角形（或多边形）绕着公共顶点旋转某一角度后能完全重合，则这两个三角形构成手拉手全等，也叫旋转型全等。

其中：公共顶点A记为“头”，每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”，第二个顶点记为“右手”。

手拉模型解题思路：SAS型全等（核心在于导角，即等角加（减）公共角）。

1）双等边三角形型条件：△ABC和△DCE均为等边三角形，C为公共点；连接BE，AD交于点F。

结论：①△ACD≌△BCE；②BE=AD；③∠AFM=∠BCM=60°；④CF平分∠BFD。

2）双等腰直角三角形型条件：△ABC和△DCE均为等腰直角三角形，C为公共点；连接BE，AD交于点N。

结论：①△ACD≌△BCE；②BE=AD；③∠ANM=∠BCM=90°；④CN平分∠BND。

3）双等腰三角形型条件：△ABC 和△DCE 均为等腰三角形，C 为公共点；连接BE ，AD 交于点F 。

结论：①△ACD ≌△BCE ；②BE =AD ；③∠ACM =∠BFM ；④CF 平分∠AFD 。

4）双正方形形型条件：△ABCFD 和△CEFG 都是正方形，C 为公共点；连接BG ，ED 交于点N 。

结论：①△△BCG ≌△DCE ；②BG =DE ；③∠BCM =∠DNM=90°；④CN 平分∠BNE 。

例1．（2022·黑龙江·中考真题）ABC V 和ADE V 都是等边三角形．(1)将ADE V 绕点A 旋转到图①的位置时，连接BD ，CE 并延长相交于点P （点P 与点A 重合），有PA PB PC +=（或PA PC PB +=）成立；请证明．(2)将ADE V 绕点A 旋转到图②的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？并加以证明；(3)将ADE V 绕点A 旋转到图③的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？直接写出结论，不需要证明．【答案】(1)证明见解析 (2)图②结论：PB PA PC =+，证明见解析 (3)图③结论：PA PB PC+=【分析】（1）由△ABC 是等边三角形，得AB =AC ，再因为点P 与点A 重合，所以PB =AB ，PC =AC ，PA =0，即可得出结论；（2）在BP 上截取BF CP =，连接AF ，证明BAD CAE V V ≌（SAS ），得ABD ACE Ð=Ð，再证明CAP BAF ≌△△（SAS ），得CAP BAF Ð=Ð，AF AP =，然后证明AFP V 是等边三角形，得PF AP =，即可得出结论；（3）在CP 上截取CF BP =，连接AF ，证明BAD CAE V V ≌（SAS ），得ABD ACE Ð=Ð，再证明BAP CAF ≌△△（SAS ），得出CAF BAP Ð=Ð，AP AF =，然后证明AFP V 是等边三角形，得PF AP =，即可得出结论：PA PB PF CF PC +=+=．(1)证明：∵△ABC 是等边三角形，∴AB =AC ，∵点P 与点A 重合，∴PB =AB ，PC =AC ，PA =0，∴PA PB PC +=或PA PC PB +=；(2)解：图②结论：PB PA PC=+证明：在BP 上截取BF CP =，连接AF ，∵ABC V 和ADE V 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð，∴BAD CAE Ð=Ð，∴BAD CAE V V ≌（SAS ），∴ABD ACE Ð=Ð，∵AC =AB ，CP =BF ， ∴CAP BAF ≌△△（SAS ），∴CAP BAF Ð=Ð，AF AP =，∴CAP CAF BAF CAF Ð+Ð=Ð+Ð，∴60FAP BAC Ð=Ð=°，∴AFP V 是等边三角形，∴PF AP =，∴PA PC PF BF PB +=+=；(3)解：图③结论：PA PB PC +=，理由：在CP 上截取CF BP =，连接AF ，∵ABC V 和ADE V 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð，∴BAD CAE Ð=Ð，∴BAD CAE V V ≌（SAS ），∴ABD ACE Ð=Ð，∵AB =AC ，BP =CF ，∴BAP CAF ≌△△（SAS ），∴CAF BAP Ð=Ð，AP AF =，∴BAF BAP BAF CAF Ð+Ð=Ð+Ð，∴60FAP BAC Ð=Ð=°，∴AFP V 是等边三角形，∴PF AP =，∴PA PB PF CF PC +=+=，即PA PB PC +=．【点睛】本题考查等边三角形的判定与性质，全等三角形的判定与性质，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．例2．（2023·湖南·长沙市八年级阶段练习）如图1，在Rt △ABC 中，∠B ＝90°，AB ＝BC ＝4，点D ，E 分别为边AB ，BC 上的中点，且BD ＝BE ．(1)如图2，将△BDE 绕点B 逆时针旋转任意角度α，连接AD ，EC ，则线段EC 与AD 的关系是 ；(2)如图3，DE ∥BC ，连接AE ，判断△EAC 的形状，并求出EC 的长；(3)继续旋转△BDE ，当∠AEC ＝90°时，请直接写出EC 的长．例3．（2023·黑龙江·虎林市九年级期末）已知Rt △ABC 中，AC =BC ，∠ACB ＝90°，F 为AB 边的中点，且DF =EF ，∠DFE ＝90°，D 是BC 上一个动点．如图1，当D 与C 重合时，易证：CD 2＋DB 2＝2DF 2；（1）当D 不与C 、B 重合时，如图2，CD 、DB 、DF 有怎样的数量关系，请直接写出你的猜想，不需证明．（2）当D 在BC 的延长线上时，如图3，CD 、DB 、DF 有怎样的数量关系，请写出你的猜想，并加以证明．【答案】（1）CD 2+DB 2=2DF 2 ；（2）CD 2+DB 2=2DF 2，证明见解析【分析】（1）由已知得222DE DF =，连接CF ，BE ，证明CDF BEF D @D 得CD =BE ，再证明BDE D 为直角三角形，由勾股定理可得结论；（2）连接CF ，BE ，证明CDF BEF D @D 得CD =BE ，再证明BDE D 为直角三角形，由勾股定理可得结论．【详解】解：（1）CD 2+DB 2=2DF 2证明：∵DF =EF ，∠DFE ＝90°，∴222DF EF DE += ∴222DE DF = 连接CF ，BE ，如图∵△ABC 是等腰直角三角形，F 为斜边AB 的中点∴CF BF =，CF AB ^，即90CFB Ð=° ∴45FCB FBC Ð=Ð=°，90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =，45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =，222DE DF =∴CD 2+DB 2=2DF 2 ；（2）CD 2+DB 2=2DF 2 证明：连接CF 、BE∵CF =BF ，DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ，∠DCF =∠EBF =135°∵∠EBD =∠EBF －∠FBD =135°－45°=90° 在Rt △DBE 中，BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键，学会添加常用辅助线，构造全等三角形解决问题．例4．（2022·青海·中考真题）两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形.(1)问题发现：如图1，若ABC V 和ADE V 是顶角相等的等腰三角形，BC ，DE 分别是底边.求证：BD CE =；(2)解决问题：如图2，若ACB △和DCE V 均为等腰直角三角形，90ACB DCE Ð=Ð=°，点A ，D ，E 在同一条直线上，CM 为DCE V 中DE 边上的高，连接BE ，请判断∠AEB 的度数及线段CM ，AE ，BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°；2AE AD DE BE CM=+=+【分析】（1）先判断出∠BAD =∠CAE ，进而利用SAS 判断出△BAD ≌△CAE ，即可得出结论；（2）同（1）的方法判断出△BAD ≌△CAE ，得出AD =BE ，∠ADC =∠BEC ，最后用角的差，即可得出结论．【解析】(1)证明：∵ABC V 和ADE V 是顶角相等的等腰三角形，∴AB AC =，AD AE =，BAC DAE Ð=Ð，∴BAC CAD DAE CAD Ð-Ð=Ð-Ð，∴BAD CAE Ð=Ð．在BAD V 和CAE V 中，AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴()BAD CAE SAS ≌△△，∴BD CE =．(2)解：90AEB =°∠，2AE BE CM =+，理由如下：由（1）的方法得，≌ACD BCE V V ，∴AD BE =，ADC BEC ÐÐ=，∵CDE △是等腰直角三角形，∴45CDE CED Ð=Ð=°，∴180135ADC CDE Ð=°-Ð=°，∴135BEC ADC Ð=Ð=°，∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°．∵CD CE =，CM DE ^，∴DM ME =．∵90DCE Ð=°，∴DM ME CM ==，∴2DE CM =．∴2AE AD DE BE CM =+=+．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质，等腰三角形，等边三角形，等腰直角三角形的性质，判断出△ACD ≌△BCE 是解本题的关键．3）15°模型2.半角模型【模型解读】半角模型概念：过多边形一个顶点作两条射线，使这两条射线夹角等于该顶角一半思想方法：通过旋转构造全等三角形，实现线段的转化1）正方形半角模型条件：四边形ABCD是正方形，∠ECF=45°；结论：①△BCE≌△DCG；②△CEF≌△CGF；③EF＝BE＋DF；④D AEF的周长=2AB；⑤CE、CF分别平分∠BEF和∠EFD。

∴△PDQ为等边三角形，∴∠PQD=60°.
∵∠DQC=∠APD=180°-15°-15°=150°，
∴∠PQC=360°-60°-150°=150°=∠DQC,，
∵PQ=QD=CQ，∴∠PCQ＝∠DCQ＝15°∴∠PCD=30°∴∠PCB=60°
∵PC=BC=CD∴ΔPBC为等边三角形
例5、已知：如图，E是正方形ABCD的边BC上一点，AF平分∠EAD交CD于点F，说明AE＝BE＋DF的理由。
8.如图，△COD是△AOB绕点O顺时针方向旋转40°后所得的图形，点C恰好在AB上，∠AOD＝90°，则∠D的度数是．
9.如图，将矩形ABCD绕点A顺时针旋转90゜后，得到矩形AB′C ′D′，如果CD=2DA=2，
那么CC′=_________．
(第13题)
10.如图是中国共产主义青年团团旗上的图案（图案本身没有字母）则至少旋转____________度后能与原来图形重合．
【分析】：由于要证的3条线段AB、BE、DF分散在两个三角形中，可利用旋转变换，将其放到一个三角形中。
【解析】：把△ADF绕点A顺时针旋转90°，则点D转到了点B的位置，点F转到了点F'的位置，根据旋转的性质得：
∠3＝∠1，F'B＝FD，∠AF'B＝∠AFD
∵ABCD为正方形
∴∠D＝∠ABF'＝90°
（1）如图（1），两三角尺的重叠部分为 ，则重叠部分的面积为，周长为．
（2）将图（1）中的 绕顶点 逆时针旋转 ，得到图（2），此时重叠部分的面积为，周长为．
（3）如果将 绕 旋转到不同于图（1）和图（2）的图形，如图（3），请你猜想此时重叠部分的面积为．
3、如图，P是等边△ABC内一点，PA=2， ，PC=4，求BC的长。

旋转一．半角模型“半角”旋转模型，经常会出现在等腰直角三角形、正方形中，在一般的等腰三角形中也会有涉及．二．等腰三角形旋转模型等腰三角形的旋转模型比较多，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化，证明的基本思想“SAS”．1．一般等腰三角形的旋转2．等边三角形的旋转3．等腰直角三角形的旋转三．对角互补模型四边形对角互补模型多数题目给出的条件会以四边形或三角形等旋转为载体．四．旋转相似模型共顶点相似的一般三角形模型：如图，图中ABD ACE∆∆∽，得到AB AD BDAC AE CE==，ABD ACE∠=∠，ADB AEC∠=∠，BAD CAE∠=∠，则有ABC ADE∆∆∽．一．考点：1．旋转全等模型；2．旋转相似模型；3．旋转中的轨迹与最值问题；二．重难点：1．这类题的关键是找到题目中所给的特殊条件，结合问题所要证明或者求解的边长角度问题，再去选择是要构造旋转全等还是通过已经得到的旋转全等的性质进一步证明．2．观察图形发现旋转得到的相似；3．通过添加辅助线构造旋转相似或者去挖掘隐含的相似图形．三．易错点：1．在利用旋转构造全等的时候注意辅助线的做法问题；2．构造旋转全等时候一定要有相等边长的条件．3．全等是相似的一个特例，旋转有时候也会出现全等，注意和旋转全等的区别和联系．题模一：旋转与全等例1.1.1已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．【答案】图2成立，证明见解析，图3不成立，图3中AE、CF、EF的关系是AE﹣CF=EF【解析】∵AB⊥AD，BC⊥CD，AB=BC，AE=CF，在△ABE和△CBF中，∴△ABE≌△CBF（SAS）；∴∠ABE=∠CBF，BE=BF；∵∠ABC=120°，∠MBN=60°，∴∠ABE=∠CBF=30°，∴AE=12BE，CF=12BF；∵∠MBN=60°，BE=BF，∴△BEF为等边三角形；∴AE+CF=12BE+12BF=BE=EF；图2成立，图3不成立．证明图2．延长DC至点K，使CK=AE，连接BK，在△BAE和△BCK中，则△BAE≌△BCK，∴BE=BK，∠ABE=∠KBC，∵∠FBE=60°，∠ABC=120°，∴∠FBC+∠ABE=60°，∴∠FBC+∠KBC=60°，∴∠KBF=∠FBE=60°，在△KBF和△EBF中，∴△KBF≌△EBF，∴KF=EF，∴KC+CF=EF，即AE+CF=EF．图3不成立，AE、CF、EF的关系是AE﹣CF=EF．例1.1.2（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD．求证：EF=BE+FD；（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【答案】（1）证明见解析（2）成立（3）EF=BE﹣FD 【解析】（1）延长EB到G，使BG=DF，连接AG．∵∠ABG=∠ABC=∠D=90°，AB=AD，∴△ABG≌△ADF．∴AG=AF，∠1=∠2．∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD．∴∠GAE=∠EAF．又AE=AE，∴△AEG≌△AEF．∴EG=EF．∵EG=BE+BG．∴EF=BE+FD（2）（1）中的结论EF=BE+FD仍然成立．（3）结论EF=BE+FD不成立，应当是EF=BE﹣FD．证明：在BE上截取BG，使BG=DF，连接AG．∵∠B+∠ADC=180°，∠ADF+∠ADC=180°，∴∠B=∠ADF．∵AB=AD，∴△ABG≌△ADF．∴∠BAG=∠DAF，AG=AF．∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD．∴∠GAE=∠EAF．∵AE=AE，∴△AEG≌△AEF．∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD．例 1.1.3如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．【答案】（1）见解析（2）见解析（3）△ACN仍为等腰直角三角形【解析】（1）证明：如图1，∵EN∥AD，∴∠MAD=∠MNE，∠ADM=∠NEM．∵点M为DE的中点，∴DM=EM．在△ADM和△NEM中，∴△ADM≌△NEM．∴AM=MN．∴M为AN的中点．（2）证明：如图2，∵△BAD和△BCE均为等腰直角三角形，∴AB=AD，CB=CE，∠CBE=∠CEB=45°．∵AD∥NE，∴∠DAE+∠NEA=180°．∵∠DAE=90°，∴∠NEA=90°．∴∠NEC=135°．∵A，B，E三点在同一直线上，∴∠ABC=180°﹣∠CBE=135°．∴∠ABC=∠NEC．∵△ADM≌△NEM（已证），∴AD=NE．∵AD=AB，∴AB=NE．在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．（3）△ACN仍为等腰直角三角形．证明：如图3，延长AB交NE于点F，∵AD∥NE，M为中点，∴易得△ADM≌△NEM，∴AD=NE．∵AD=AB，∴AB=NE．∵AD∥NE，∴AF⊥NE，在四边形BCEF中，∵∠BCE=∠BFE=90°∴∠FBC+∠FEC=360°﹣180°=180°∵∠FBC+∠ABC=180°∴∠ABC=∠FEC在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．例1.1.4如图，△AEF中，∠EAF=45°，AG⊥EF于点G，现将△AEG沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE和DF相交于点C．（1）求证：四边形ABCD是正方形；（2）连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．（3）若EG=4，GF=6，2，求AG、MN的长．【答案】（1）见解析（2）MN2=ND2+DH2；理由见解析（3）AG=12；2【解析】（1）证明：∵△AEB由△AED翻折而成，∴∠ABE=∠AGE=90°，∠BAE=∠EAG，AB=AG，∵△AFD由△AFG翻折而成，∴∠ADF=∠AGF=90°，∠DAF=∠FAG，AD=AG，∵∠EAG+∠FAG=∠EAF=45°，∴∠ABE=∠AGE=∠BAD=∠ADC=90°，∴四边形ABCD 是矩形，∵AB=AD ，∴四边形ABCD 是正方形；（2）MN 2=ND 2+DH 2，理由：连接NH ，∵△ADH 由△ABM 旋转而成，∴△ABM ≌△ADH ，∴AM=AH ，BM=DH ，∵由（1）∠BAD=90°，AB=AD ，∴∠ADH=∠ABD=45°，∴∠NDH=90°，∴△AMN ≌△AHN ，∴MN=NH ，∴MN 2=ND 2+DH 2；（3）设AG=BC=x ，则EC=x ﹣4，CF=x ﹣6，在Rt △ECF 中，∵CE 2+CF 2=EF 2，即（x ﹣4）2+（x ﹣6）2=100，x 1=12，x 2=﹣2（舍去）∴AG=12，∵AG=AB=AD=12，∠BAD=90°，∴22AB AD +221212+2，∵2，∴MD=BD ﹣2﹣22，设NH=y，在Rt△NHD中，∵NH2=ND2+DH2，即y2=（2y）2+（22，解得2，即2．题模二：旋转与相似例1.2.1如图1，点P在正方形ABCD的对角线AC上，正方形的边长是a，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N．（1）操作发现：如图2，固定点P，使△PEF绕点P旋转，当PM⊥BC时，四边形PMCN是正方形．填空：①当AP=2PC时，四边形PMCN的边长是________；②当AP=nPC时（n是正实数），四边形PMCN的面积是___________．（2）猜想论证如图3，改变四边形ABCD的形状为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF 的两条直角边PE、PF分别交BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则PMPN=__________．（3）拓展探究如图4，当四边形ABCD满足条件：∠B+∠D=180°，∠EPF=∠BAD时，点P在AC上，PE、PF分别交BC，CD于M、N点，固定P点，使△PEF绕点P旋转，请探究PMPN的值，并说明理由．【答案】（1）①13a②()221an+（2）ab（3）见解析【解析】（1）①如图2，∵PM⊥BC，AB⊥BC ∴△PMC∽△ABC又∵AP=2PC∴PMAB=13，即PMa=13∴PM=13a，即正方形PMCN的边长是13a②当AP=nPC时（n是正实数），PMAB=11n+∴PM=11n+a∴四边形PMCN的面积=（11n+a）2=()221an+（2）如图3，过P作PG⊥BC于G，作PH⊥CD于H，则∠PGM=∠PHN=90°，∠GPH=90°∵Rt△PEF中，∠FPE=90°∴∠GPM=∠HPN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==∵AB=a，BC=b∴PG PHa b=，即PGPH=ab（3）如图4，过P作PG∥AB，交BC于G，作PH∥AD，交CD于H，则∠HPG=∠DAB ∵∠EPF=∠BAD∴∠EPF=∠GPH，即∠EPH+∠HPN=∠EPH+∠GPM∴∠HPN=∠GPM∵∠B+∠D=180°∴∠PGC+∠PHC=180°又∵∠PHN+∠PHC=180°∴∠PGC=∠PHN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==即PG AB PH AD=②∴由①②可得，PMPN=ABAD例1.2.2数学活动课上，小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动．操作：使点D落在线段AB的中点处并使DF过点C（如图1），然后将其绕点D顺时针旋转，直至点E落在AC的延长线上时结束操作，在此过程中，线段DE与AC或其延长线交于点K，线段BC与DF相交于点G（如图2，3）．探究1：在图2中，求证：△ADK∽△BGD．探究2：在图2中，求证：KD平分∠AKG．探究3：①在图3中，KD仍平分∠AKG吗？若平分，请加以证明；若不平分，请说明理由．②在以上操作过程中，若设AC=BC=8，KG=x，△DKG的面积为y，请求出y与x的函数关系式，并直接写出x的取值范围．【答案】探究1：见解析；探究2：见解析；探究3：①KD仍平分∠AKG②y=2x，其中≤≤4838x【解析】探究1，∵∠KAD=∠KDG=∠DBG=45°，∴∠KDA+∠BDG=135°．∵∠BDG+∠BGD=135°，∴∠KDA=∠BGD，∴△ADK∽△BGD；探究2，∵△ADK∽△BGD，∵点D是线段AB的中点，∴BD=AD，∵∠KAD=∠KDG=45°，∴△ADK∽△DCK，∴∠AKD=∠DKC，∴KD平分∠AKG．探究3，①KD仍平分∠AKG．理由如下：∵同探究1可得△ADK∽△BGD，同探究2可得，△ADK∽△DGK，∴∠AKD=∠DKG，∴KD仍平分∠AKG；②如图，过点D作DM⊥AC于点M，DN⊥KG于点N，由①知线段KD平分∠AKG，∴DM=DN．∵AC=BC=8，点D是线段AB的中点，∠KAD=45°，∴DM=DN=4．∵KG=x，∴S△DKG=y=12×4x=2x，对于图3的情况同理可得y=2x，综上所示，y=2x，其中38．题模三：旋转中的轨迹与最值问题例1.3.1如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为．【答案】18﹣2【解析】如图，作AP1⊥BD垂足为P1，∵∠DBA=45°，AB=10，∴∠P1AB=∠DBA=45°，AP1=P12，∵AM=MD=12AD=4，当AP1旋转到与射线AD的重合时（点P1与点E重合），ME就是MQ最小值24，当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值=AM+AF=14，∴MQ的最大值与最小值的差=14﹣（2﹣4）=18﹣2故答案为18﹣2例 1.3.2如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为______；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为______．（结果都保留π）【答案】3231+nπ【解析】∵菱形ABCD中，AB=2，∠C=60°，∴△ABD是等边三角形，BO=DO=1，223AD DO-第一次旋转的弧长6033ππ⨯=∵第一、二次旋转的弧长和60360323ππ⨯⨯=，第三次旋转的弧长为：601 1803ππ⨯=∵3n÷3=n，故经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为：n 23π+3π）231+nπ．例1.3.3如图1，点O为正方形ABCD的中心．（1）将线段OE绕点O逆时针方向旋转90︒，点E的对应点为点F，连结EF，AE，BF，请依题意补全图1；（2）根据图1中补全的图形，猜想并证明AE与BF的关系；（3）如图2，点G是OA中点，△EGF是等腰直角三角形，H是EF的中点，90EGF∠=︒，22AB=2GE=，△EGF绕G点逆时针方向旋转α角度，请直接写出旋转过程中BH的最大值．【答案】（1）见解析（2）AE⊥BF（3）25+【解析】（1）正确画出图形；………………1分（2）延长EA 交OF 于点H ，交BF 于点G …2分∵O 为正方形ABCD 的中心，∴OB OA =，∠AOB ＝90……3分∵OE 绕点O 逆时针旋转90角得到OF∴∠AOB ＝∠EOF ＝90∴∠EOA ＝∠FOB ……4分在△EOA 和△FOB 中，∴BF AE =.……5分∴∠OFB +∠FHG =90∴AE ⊥BF ……6分（3）BH 的最大值为25+……8分随练1.1 在ABC ∆中，2AB BC ==，90ABC ∠=︒，BD 为斜边AC 上的中线，将ABD ∆绕点D 顺时针旋转α(0180α︒<<︒)得到EFD ∆，其中点A 的对应点为点E ，点B 的对应点为点F ，BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________;（2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN =__________;（3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系：____________________________.【答案】 （1）BE FC =；（2）22FC ；（3）222BF CE AC +=. 【解析】 （1）BE FC =；（2）证明：如图，∵AB BC =，90ABC ∠=︒，BD 为斜边中线，∴12BD AD CD AC ===，BD AC ⊥ ∵EFD ∆是由ABD ∆旋转得到的，∴DE DF DB DC ===，90EDF ADB BDC ∠=∠=∠=︒∴EDF BDF BDC BDF ∠+∠=∠+∠，即BDE FDC ∠=∠，∴BDE FDC ∆∆≌，∴BE FC =且12∠=∠又∵34∠=∠，∴90FHE FDE ∠=∠=︒ ,即BE CF ⊥连接BF ，取BF 中点G ，连接MG 、NG .∵M 为EF 中点，G 为BF 中点，N 为BC 中点又∵EB FC =，BE FC ⊥∴MG NG =，90MGN ∠=︒，∴MGN ∆为等腰直角三角形，∴2MN =. （3）222BF CE AC +=.随练1.2 在菱形ABCD 中，120BAD ∠=︒，4AB =，把一个含60°角的三角板与这个菱形叠合，使三角板的60°角的顶点与点A 重合，两边分别落在AB 、AC 上．将三角板绕点A 按逆时针旋转，设旋转角为α．（1）如图①，当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你通过观察或测量写出图中现有的两组相等线段(菱形的边和对角线除外)．（2）如图②，当60120α︒<<︒时，三角板的两边分别与BC 、CD 的延长线相交于点E 、F ，你在(1)中得到的结论还成立吗?若成立，请你选择一组加以证明；若不成立，请你说明理由．（3）当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你求出这个三角板与这个菱形重合部分的面积．【答案】 见解析【解析】 （1）BE CF =，AE AF =，CE DF =．写出两组即可．（2）（1）中的结论仍然成立．如图，BE CF =的结论仍然成立．证明如下：∵在菱形ABCD 中，120BAD ∠=︒，又由题意可知，60EAF ∠=︒，∴BAE CAF ∠=∠．在△BAE 和△CAF 中，∴△BAE ≌△CAF ．∴BE CF =．（3）当060α︒<<︒时，三角板与这个菱形重合部分的面积就是四边形AECF 的面积．由题意可证△BAE ≌△CAF ．∴四边形AECF 的面积就是△ABC 的面积．∵4AB =，∴所求图形的面积为43随练1.3如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）（1）如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；（2）如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．【答案】（1）DM=FM，DM⊥FM（2）DM⊥FM，DM=FM【解析】（1）如图2，DM=FM，DM⊥FM，证明：连接DF，NF，∵四边形ABCD和CGEF是正方形，∴AD∥BC，BC∥GE，∴AD∥GE，∴∠DAM=∠NEM，∵M是AE的中点，∴AM=EM，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∠DCF=∠DCB=90°，在△DCF与△NEF中，∴△DCF≌△NEF，∴DF=NF，∠CFD=∠EFN，∵∠EFN+∠NFC=90°，∴∠DFC+∠CFN=90°，∴∠DFN=90°，∴DM⊥FM，DM=FM（2）猜想：DM⊥FM，DM=FM，证明如下：如图3，连接DF，NF，连接DF，NF，∵四边形ABCD是正方形，∴AD∥BC，∵点E、B、C在同一条直线上，∴AD∥CN，∴∠ADN=∠MNE，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∵∠DCF=90°+45°=135°，∠NEF=180°﹣45°=135°，∴∠DCF=∠NEF，在△DCF与△NEF中，∴△MAD≌△MEN，∴DF=NF，∠CFD=∠EFN，∵∠CFD+∠EFD=90°，∴∠NFE+∠EFD=90°，∴∠DFN=90°，∴DM ⊥FM ，DM=FM ．随练 1.4 已知：在ABC △中，AB AC =，点D 为BC 边的中点，点F 在AB 上，连结DF 并延长到点E ,使BAE BDF ∠=∠，点M 在线段DF 上，且ABE DBM ∠=∠．（1）如图，当45ABC ∠=°时， 求证：2AE MD =；（2）如图，当60ABC ∠=°时，则线段AE MD 、之间的数量关系为____________；（3）在（2）的条件下，延长BM 到P ，使MP BM =，连接CP ，若727AB AE ==，，求tan EAB ∠的值．【答案】 （1）见解析（2）2AE MD =（33 【解析】 该题考查的是四边形综合．（1）如图，连结AD又∵45ABC ∠=°∴cos BD AB ABC =∠即2AB BD =∴△ABE ∽△DBM（2）与（1）类似可知△DBM ∽△ABE ，又60ABC ∠=︒，（3）如图2连结AD 、EP ，∵△ABE ∽△DBM又∵BM MP =∴△BEP 等边三角形∴EM BP ⊥即90BMD ∠=︒在Rt △AEB 中，27AE =7AB =， tan EAB ∠的值为3随练 1.5 在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别在直线AB AC ，上移动时，BM NC MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．（1）如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时Q L=__________ （2）如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明；（3）如图③，当点M N ，分别在边AB CA ，的延长线上时，若AN x =，则Q =_________（用x L ，表示）【答案】 见解析【解析】 (Ⅰ)BM 、NC 、MN 之间的数量关系BM NC MN +=．此时23Q L =． (Ⅱ)猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE BM =，连结DE ．∵BD CD =，且120BDC ∠=︒．又△ABC 是等边三角形，∴90MBD NCD ∠=∠=︒．在△MBD 与△ECD 中，BM CE MBD ECD BD DC =⎧⎪∠=∠⎨⎪=⎩∴△MBD ≌△ECD (SAS)．∴DM DE =，BDM CDE ∠=∠．在△MDN 与△EDN 中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩∴△MDN ≌△EDN (SAS)．△AMN 的周长Q AM AN MN =++而等边△ABC 的周长3L AB =(Ⅲ)如图③，当M 、N 分别在AB 、CA 的延长线上时，若AN x =，则223Q x L=+（用x、L表示）．随练1.6（1）正方形ABCD中，对角线AC与BD相交于点O，如图1，请直接猜想并写出AO与CD 之间的数量关系：；（2）如图2，将（1）中的△BOC绕点B逆时针旋转得到△BO1C1，连接AO1，DC1，请猜想线段AO1与DC1的数量关系，并证明你的猜想；（3）如图3，矩形ABCD和Rt△BEF有公共顶点，且∠BEF=90°，∠EBF=∠ABD=30°，则AEDF=______．【答案】（1）AO=2CD．理由如下：∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3【解析】（1）根据正方形的性质得AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，由勾股定理得到AO与CD之间的数量关系；（2）如图2根据正方形的性质得AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，得到△ABC和△OBC都是等腰直角三角形，求出AC=2AB BC=2BO，得到BD=2AB，因为△BOC绕点B逆时针方向旋转得到△BO1C1，所以∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，BC1=2BO1，由∠1+∠3=45°，∠2+∠3=45°，得到∠1=∠2，于是得到△BDC1∽△BAO1，求出结论；（3）如图3在R t△ABD中，cos∠ABD=ABBD，在Rt△EBF中，cos∠EBF=EBFB因为∠EBF=∠ABD=30°得到BE ADBF BD=3，再由∠EBF+∠FBA=∠ABD+∠FBA，得到∠EBA=∠FBD，△AEB∽△FBD，由相似的性质得到解．解：（1）AO=2CD．理由如下：如图1，∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）如图2，∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）如图3 在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3．随练1.7如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF 相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是______．【答案】2【解析】如图点P运动的路径是以G为圆心的弧EF，在⊙G上取一点H，连接EH、FH．∵四边形AOCB是正方形，∴∠AOC=90°，∴∠AFP=12∠AOC=45°，∵EF是⊙O直径，∴∠EAF=90°，∴∠APF=∠AFP=45°，∴∠H=∠APF=45°，∴∠EGF=2∠H=90°，∵EF=4，GE=GF，∴2，∴EF的长9022π•2．随练1.8已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．【答案】（1）见解析；（2）①∠CMD=135°②2π【解析】（1）如图1中，∵CA=CB，∠ACB=90°，∴∠A=∠ABC=45°，∵△CEF是由△CAD旋转逆时针α得到，α=90°，∴CB与CE重合，∴∠CBE=∠A=45°，∴∠ABF=∠ABC+∠CBF=90°，∵BG=AD=BF，∴∠BGF=∠BFG=45°，∴∠A=∠BGF=45°，∴GF∥AC．（2）①如图2中，∵CA=CE，CD=CF，∴∠CAE=∠CEA，∠CDF=∠CFD，∵∠ACD=∠ECF，∴∠ACE=∠CDF，∵2∠CAE+∠ACE=180°，2∠CDF+∠DCF=180°，∴∠CAE=∠CDF，∴A、D、M、C四点共圆，∴∠CMF=∠CAD=45°，∴∠CMD=180°﹣∠CMF=135°．②如图3中，O是AC中点，连接OD、CM．∵AD=DB，CA=CB，∴CD⊥AB，∴∠ADC=90°，由①可知A、D、M、C四点共圆，∴当α从90°变化到180°时，点M 在以AC 为直径的⊙O 上，运动路径是弧CD ，∵OA=OC ，CD=DA ，∴DO ⊥AC ，∴∠DOC=90°，∴CD ∧的长=901180π=2π． ∴当α从90°变化到180°时，点M 运动的路径长为2π． 随练1.9 如图1，点O 是正方形ABCD 两对角线的交点，分别延长OD 到点G ，OC 到点E ，使OG=2OD ，OE=2OC ，然后以OG 、OE 为邻边作正方形OEFG ，连接AG ，DE ．（1）求证：DE ⊥AG ；（2）正方形ABCD 固定，将正方形OEFG 绕点O 逆时针旋转α角（0°＜α＜360°）得到正方形OE ′F ′G ′，如图2．①在旋转过程中，当∠OAG ′是直角时，求α的度数；②若正方形ABCD 的边长为1，在旋转过程中，求AF ′长的最大值和此时α的度数，直接写出结果不必说明理由．【答案】 （1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①α=30°；②α=315°．【解析】 （1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①在旋转过程中，∠OAG′成为直角有两种情况：（Ⅰ）α由0°增大到90°过程中，当∠OAG′=90°时，∵OA=OD=12OG=12OG′， ∴在Rt △OAG′中，sin ∠AG′O='OA OG =12， ∴∠AG′O=30°，∵OA ⊥OD ，OA ⊥AG′，∴OD ∥AG′，∴∠DOG′=∠AG′O=30°，即α=30°；（Ⅱ）α由90°增大到180°过程中，当∠OAG′=90°时，同理可求∠BOG′=30°，∴α=180°﹣30°=150°．综上所述，当∠OAG′=90°时，α=30°或150°．②如图3，当旋转到A、O、F′在一条直线上时，AF′的长最大，∵正方形ABCD的边长为1，∴2，∵OG=2OD，∴2∴OF′=2，∴2+2，∵∠COE′=45°，∴此时α=315°．作业1如图1，在△ABC中，∠BAC=90°，AB=AC．（1）若点M为AC上的任意一点，过M作MN⊥BC于点N，取BM的中点D，连接AD、DM，求证：AD=DN．（2）如图2，若M为BC上的任意一点，以线段CM为底边作等腰Rt△MCN，此时，取BM的中点D，连接AD、DN，则AD与DN有怎样的数量关系？说明理由．（3）如图3，在（2）的条件下将Rt△MNC绕C点旋转任意角度，连接BM，取BM的中点D，再连接AD、DN，则（2）中的结论仍然成立吗，它们之间又有怎样的位置关系？请说明理由．【答案】（1）见解析；（2）AD=DN；（3）AD=DN，AD⊥DN【解析】（1）证明：解法一：如图1中，延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMC=∠BAC=90°，∵AB=AC，∠BAC=90°，∴∠C=45°，∵MN⊥BC，∴∠MNC=90°，∠NMC=45°=∠KMC=∠C，∴MN=NC，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．解法二：根据直角三角形斜边中线性质，可知AD=12BM，DN=12BM，由此即可证明．（2）如图2中，结论：AD=DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMN=∠B=45°，∵∠NMC=∠NCM=∠ACB=45°∴MN=NC，∠KMN=∠ACN=90°在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．（3）如图3中，结论：AD=DN，AD⊥DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM，延长KN交AC于G．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KGC=∠BAC=90°，∴∠ACN+∠NMG=180°，∵∠KMN+∠NMG=180°，∴∠ACN=∠NMK，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，DN⊥AK，即AD=DN．AD⊥DN．作业2已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．【答案】（1）见解析（2）成立（3）见解析【解析】本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质．（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG=CG；再证出△DMG≌△FNG，得到MG=NG；再证明△AMG≌△ENG，得出AG=EG；最后证出CG=EG．（3）结论依然成立．还知道EG⊥CG．（1）证明：∵四边形ABCD是正方形，∴∠DCF=90°，在Rt△FCD中，∵G为DF的中点，∴CG=12 FD，同理，在Rt△DEF中，EG=12 FD，∴CG=EG．（1）（1）中结论仍然成立，即EG=CG．证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG（SAS），∴AG=CG；在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG（ASA），∴MG=NG；∵∠EAM=∠AEN=∠AMN=90°，∴四边形AENM是矩形，在矩形AENM中，AM=EN，在△AMG与△ENG中，∵AM=EN，∠AMG=∠ENG，MG=NG，∴△AMG≌△ENG（SAS），∴AG=EG，∴EG=CG．证法二：延长CG至M，使MG=CG，连接MF，ME，EC，在△DCG与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，∴△DCG≌△FMG．∴MF=CD，∠FMG=∠DCG，∴MF∥CD∥AB，∴EF⊥MF．在Rt△MFE与Rt△CBE中，∵MF=CB，∠MFE=∠EBC，EF=BE，∴△MFE≌△CBE∴∠MEF=∠CEB．∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，∴△MEC为直角三角形．∵MG=CG，∴EG=12 MC，∴EG=CG．（3）（1）中的结论仍然成立．理由如下：过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N．由于G为FD中点，易证△CDG≌△MFG，得到CD=FM，又因为BE=EF，易证∠EFM=∠EBC，则△EFM≌△EBC，∠FEM=∠BEC，EM=EC∵∠FEC+∠BEC=90°，∴∠FEC+∠FEM=90°，即∠MEC=90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG=CG，EG⊥CG．作业3在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？答：____（填“成立”或“不成立”）【答案】（1）见解析；（2）不成立；（3）成立【解析】（1）证明：如图1，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵O为AB中点，∴OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（2）还成立，理由是：如图2，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（3）成立．作业4在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．请直接写出AC1与BD1的数量关系和位置关系．（2）如图2，若四边形ABCD是菱形，AC=6，BD=8，判断AC1与BD1的数量关系和位置关系，并给出证明；（3）如图3，若四边形ABCD是平行四边形，AC=6，BD=12，连接DD1，设AC1=kBD1，请直接写出k 的值和AC12+（kDD1）2的值．【答案】（1）AC1⊥BD1（2）AC1=34BD1，AC1⊥BD1，理由见解析（3）AC12+（kDD1）2=36【解析】（1）AC1=BD1，AC1⊥BD1；理由：如图1，∵四边形ABCD是正方形，∴OC=OA=OD=OB，AC⊥BD，∴∠AOB=∠COD=90°，∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OC1=OC，OD1=OD，∠COC1=∠DOD1，∴OC1=OD1，∠AOC1=∠BOD1=90°+∠AOD1，在△AOC 1和△BOD 1中1111AO OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩ ，∴△AOC 1≌△BOD 1（SAS ）；∴AC 1=BD 1，∵∠AOB=90°，∴∠OAB+∠ABP+∠OBD 1=90°，∴∠OAB+∠ABP+∠OAC 1=90°，∴∠APB=90°，则AC 1⊥BD 1；故AC 1 与BD 1的数量关系是：AC 1=BD 1；AC 1 与BD 1的位置关系是：AC 1⊥BD 1；（2）AC 1=34BD 1，AC 1⊥BD 1． 理由：∵四边形ABCD 是菱形，∴OC=OA=12AC ，OD=OB=12BD ，AC ⊥BD ． ∵△C 1OD 1由△COD 绕点O 旋转得到，∴O C 1=OC ，O D 1=OD ，∠CO C 1=∠DO D 1．∴O C 1=OA ，O D 1=OB ，∠AO C 1=∠BO D 1，∴△AO C 1∽△BOD 1．∴∠O AC 1=∠OB D 1．又∵∠AOB=90°，∴∠O AB+∠ABP+∠OB D 1=90°．∴∠O AB+∠ABP+∠O AC 1=90°．∴∠APB=90°．∴AC 1⊥BD 1．∵△AO C 1∽△BOD 1，即AC 1=34BD 1，AC 1⊥BD 1．（3）如图3，与（2）一样可证明△AOC1∽△BOD1，∴k=12；∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OD1=OD，而OD=OB，∴OD1=OB=OD，∴△BDD1为直角三角形，在Rt△BDD1中，BD12+DD12=BD2=144，∴（2AC1）2+DD12=144，∴AC12+（kDD1）2=36．作业5在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．（一）尝试探究如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD 上，∠EAF=30°，连接EF．（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=________度，线段BE、EF、FD之间的数量关系为________．（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．（二）拓展延伸如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．【答案】解：（一）（1）：30 ，BE+DF=EF（2）BE﹣DF=EF（二）3【解析】解：（一）（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′，则∠1=∠2，BE=DE′，AE=AE′，∵∠BAD=60°，∠EAF=30°，∴∠1+∠3=30°，∴∠2+∠3=30°，即∠FAE′=30°∴∠EAF=∠FAE′，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，即EF=DF+DE′，∴EF=DF+BE，即线段BE、EF、FD之间的数量关系为BE+DF=EF，故答案为：30，BE+DF=EF；（2）如图3，在BE上截取BG=DF，连接AG，在△ABG和△ADF中，∴△ABG≌△ADF（SAS），∴∠BAG=∠DAF，且AG=AF，∵∠DAF+∠DAE=30°，∴∠BAG+∠DAE=30°，∵∠BAD=60°，∴∠GAE=60°﹣30°=30°，∴∠GAE=∠FAE，在△GAE和△FAE中，∴△GAE≌△FAE（SAS），∴GE=FE，又∵BE﹣BG=GE，BG=DF，∴BE﹣DF=EF，即线段BE、EF、FD之间的数量关系为BE﹣DF=EF；（二）如图4，将△ABE 绕点A 逆时针旋转60°得到△A ′B ′E ′，则AE=AE ′，∠EAE ′=60°，∴△AEE ′是等边三角形，又∵∠EAF=30°，∴AN 平分∠EAF ，∴AN ⊥EE ′，∴直角三角形ANE 中，AN 3AE = ∵在等边△ABC 中，AM ⊥BC ，∴∠BAM=30°， ∴AM 3AB =，且∠BAE+∠EAM=30°， 又∵∠MAN+∠EAM=30°，∴∠BAE=∠MAN ，∴△BAE ∽△MAN ， ∴MN AM =BE AB ，即MN 31= ∴3． 作业6 探索绕公用顶点的相似多边形的旋转：（1）如图1，已知：等边ABC ∆和ADE ∆，根据__________（指出三角形的全等或相似），可得到CE 与BD 的大小关系为：__________．（2）如图2，正方形ABCD 和正方形AEFG ，求：FCEB 的值；（3）如图3，矩形ABCD 和矩形AEFG ，AB kBC =，AE kEF =，求：FCEB 的值．【答案】 （1）全等，相等；（223）21k +．【解析】 解：（1）如图1，ABC ∆和ADE ∆都是等边三角形，在AEC ∆和ADB ∆中，AE ADCAE BADAC AB =⎧⎪∠=∠⎨=⎪⎩，AEC ADB ∴∆≅∆，CE BD ∴=；（2）如图2，四边形ABCD 和四边形AEFG 都是正方形，（3）连接FA 、CA ，如图3，四边形ABCD 和四边形AEFG 都是矩形，AB kBC =，AE kEF =，作业7 如图，边长为6的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针转60°得到FC ，连接DF ．则在点E 运动过程中，DF 的最小值是（ ）A ． 6B ． 3C ． 2D ． 1.5【答案】D【解析】 取线段AC 的中点G ，连接EG ，如图所示．∵△ABC 为等边三角形，且AD 为△ABC 的对称轴，∴CD=CG=12AB=3，∠ACD=60°， ∵∠ECF=60°，∴∠FCD=∠ECG ．在△FCD 和△ECG 中，FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩，∴△FCD ≌△ECG （SAS ），∴DF=GE ．当EG ∥BC 时，EG 最小，∵点G 为AC 的中点，∴此时EG=DF=12CD=32． 作业8 已知等边△ABC 边长为2，放置在如图的水平桌面上，将△ABC 水平向右作无滑动翻滚，使△ABC 首次落回开始的位置，则等边△ABC 的中心O 经过的路径长为_________．【答案】433π．【解析】如图，过点C作CD⊥AB于D，则CD一定经过点O，∵CD=32BC=3，∴OC=23CD=233，根据等边三角形的性质，∠BCD=12∠ACB=12×60°=30°，∴每一次翻滚中心O旋转的角度为：180°﹣2×30°=120°，等边三角形翻滚3次翻滚一周，∴点O旋转的角度为：120°×3=360°，∴中心O经过的路径长是：2π•OC=2π×233=433π，故答案为：433π．作业9已知，点O是等边△ABC内的任一点，连接OA，OB，OC．（1）如图1，已知∠AOB=150°，∠BOC=120°，将△BOC绕点C按顺时针方向旋转60°得△ADC．①∠DAO的度数是；②用等式表示线段OA，OB，OC之间的数量关系，并证明；（2）设∠AOB=α，∠BOC=β．①当α，β满足什么关系时，OA+OB+OC有最小值？请在图2中画出符合条件的图形，并说明理由；②若等边△ABC的边长为1，直接写出OA+OB+OC的最小值．【答案】（1）①90°；②OA2+OB2=OC2；证明见解析（2）①α=β=120°，OA+OB+OC有最小值；图形见解析【解析】（1）①∠AOB=150°，∠BOC=120°，∴∠AOC=360°﹣120°﹣150°=90°，。

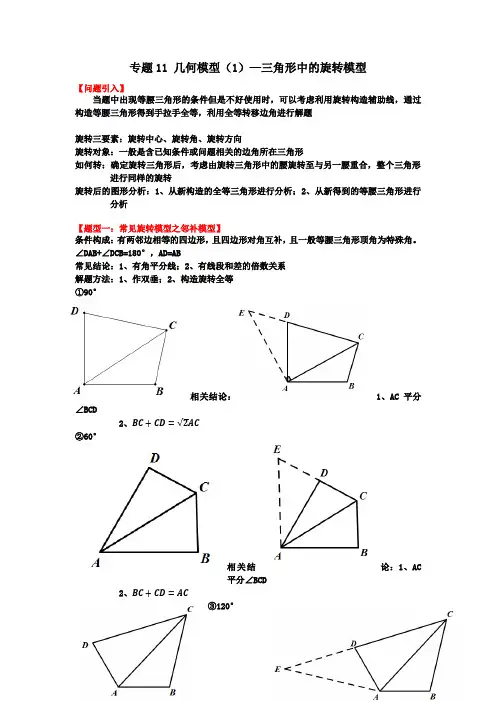
专题11 几何模型（1）—三角形中的旋转模型【问题引入】当题中出现等腰三角形的条件但是不好使用时，可以考虑利用旋转构造辅助线，通过构造等腰三角形得到手拉手全等，利用全等转移边角进行解题旋转三要素：旋转中心、旋转角、旋转方向旋转对象：一般是含已知条件或问题相关的边角所在三角形如何转：确定旋转三角形后，考虑由旋转三角形中的腰旋转至与另一腰重合，整个三角形进行同样的旋转旋转后的图形分析：1、从新构造的全等三角形进行分析；2、从新得到的等腰三角形进行分析【题型一：常见旋转模型之邻补模型】条件构成：有两邻边相等的四边形，且四边形对角互补，且一般等腰三角形顶角为特殊角。

∠DAB+∠DCB=180°，AD=AB常见结论：1、有角平分线；2、有线段和差的倍数关系解题方法：1、作双垂；2、构造旋转全等①90°相关结论：1、AC平分∠BCD2、BC+CD=√2AC②60°相关结论：1、AC平分∠BCD2、BC+CD=AC③120°相关结论：1、AC平分∠BCD2、BC+CD=√3AC补充说明：对角互补、邻边相等、角平分线三个条件知到其中两个就可求另外第三个，辅助线的构造与三角形全等相同，但是全等判定会有差异，需要根据具体情况判断【例】如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝8，AB＝AC，∠CBD＝30°，BD＝4√3，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为_____．【答案】4√3+4．【解析】将△ACN绕点A逆时针旋转，得到△ABE，如图：由旋转得：∠NAE＝90°，AN＝AE，∠ABE＝∠ACD，∠EAB＝∠CAN，∵∠BAC＝∠D＝90°，∴∠ABD+∠ACD＝360°﹣90°﹣90°＝180°，∴∠ABD+∠ABE＝180°，∴E，B，M三点共线，∵∠MAN＝45°，∠BAC＝90°，∴∠EAM＝∠EAB+∠BAM＝∠CAN+∠BAM＝∠BAC﹣∠MAN＝90°﹣45°＝45°，∴∠EAM＝∠MAN，在△AEM和△ANM中，{AE=AN∠EAM=∠NAMAM=AM，∴△AEM≌△ANM（SAS），∴MN＝ME，∴MN＝CN+BM，∵在Rt△BCD中，∠BDC＝90°，∠CBD＝30°，BD＝4√3，CD＝BD×tan∠CBD＝4，∴△DMN的周长为DM+DN+MN＝DM+DN+BM+CN＝BD+DC＝4√3+4，故答案为：4√3+4．【练1】如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．【答案】3√2【解析】解：将△OBC绕O点旋转90°，∵OB=OA∴点B落在A处，点C落在D处且有OD=OC=3，∠COD=90°，∠OAD=∠OBC，在四边形OACB中∵∠BOA=∠BCA=90°，∴∠OBC+∠OAC=180°，∴∠OAD+∠OAC=180°∴C、A、D三点在同一条直线上，∴△OCD为等要直角三角形，根据勾股定理CD2=OC2+OD2即CD2=32+32=18解得CD=3√2即BC+AC=3√2.【练2】如图，P是等边三角形ABC内一点，将线段BP绕点B逆时针旋转60°得到线段BQ，连接AQ．若PA=4，PB=5，PC=3，则四边形APBQ的面积为_______．【答案】5√34+6【解析】解：如图，连接PQ，由旋转的性质可得，BP=BQ，又∵∠PBQ=60°，∴△BPQ是等边三角形，∴PQ=BP，在等边三角形ABC中，∠CBA=60°，AB=BC，∴∠ABQ=60°-∠ABP∠CBP=60°-∠ABP∴∠ABQ=∠CBP在△ABQ与△CBP中{BQ=BP∠ABQ=∠CBPAB=CB∴△ABQ≌△CBP(SAS)，∴AQ=PC，又∵PA=4，PB=5，PC=3，∴PQ=BP=5，PC=AQ=3，在△APQ中，AQ2=9,AP2=16,PQ2=25，25=16+9，∴由勾股定理的逆定理可知△APQ是直角三角形，∴S 四边形APBQ =S △BPQ +S △APQ =√34×52+12×3×4=5√34+6， 故答案为：5√34+6【练3】如图，在△ABC 中，∠ACB =120°，BC >AC ，点E 在BC 上，点D 在AB 上，CE =CA ，连接DE ，180ACB ADE ∠+∠=︒，CH ⊥AB ，垂足为H ．证明：DE AD +=．【答案】见解析【解析】证明：如图，延长BA 到点F ，使AF=DE ，连接CF 、CD ，∵∠ACB+∠ADE=180°∴∠CAD+∠CED=360°－180°=180°∵∠CAD+∠CAF=180°∴∠CAF=∠CED∵AC=EC ，AF=ED∴△AFC ≌△EDC∴CF=CD ，∠ACF=∠ECD∴∠FCD=∠ACF+∠ACD=∠ECD+∠ACD=∠ACB=120°∵CF=CD ，CH ⊥DF∴FH=DH=12DF =12(DE+AD)，∠HCD=12∠FCD=60°∴tan ∠HCD=DH CH =√3∴DH=√3CH∴DE+AD=2DH=2√3CH【题型二：旋转与三角形全等的构造】【例】问题背景：如图①设P 是等边△ABC 内一点，PA ＝6，PB ＝8，PC ＝10，求∠APB 的度数．小君研究这个问题的思路是：将△ACP 绕点A 逆时针旋转60°得到△ABP '，易证：△APP'是等边三角形，△PBP'是直角三角形，所以∠APB＝∠APP'+∠BPP'＝150°．简单应用：（1）如图2，在等腰直角△ABC中，∠ACB＝90°．P为△ABC内一点，且PA ＝5，PB＝3，PC＝2√2，则∠BPC＝°（2）如图3，在等边△ABC中，P为△ABC内一点，且PA＝5，PB＝12，∠APB＝150°，则PC＝．拓展廷伸：①如图4，∠ABC＝∠ADC＝90°，AB＝BC．求证：√2BD＝AD+DC．②若图4中的等腰直角△ABC与Rt△ADC在同侧如图5，若AD＝2，DC＝4，请直接写出BD的长．【答案】（1）135°（2）PC=13；拓展延伸①：证明见解析②：BD=√2【解析】解：简单应用：（1）如图2，∵△ABC是等腰直角三角形，∴∠ACB＝90°，AC＝BC，将△ACP绕点C逆时针旋转90°得到△CBP'，连接PP'，∴BP'＝AP＝5，∠PCP'＝90°，CP'＝CP＝2√2，∴∠CPP'＝∠CP'P＝45°，根据勾股定理得，PP'=√2CP＝4，∵BP'＝5，BP＝3，∴PP'2+BP2＝BP'，∴△BPP'是以BP'为斜边的直角三角形，∴∠BPP'＝90°，∴∠BPC＝∠BPP'+∠CPP'＝135°，（2）如图3，∵△ABC是等边三角形，∴∠BAC＝60°，AC＝AB，将△ACP绕点A逆时针旋转60°得到△ABP'，连接PP'，∴BP'＝CP，AP'＝AP＝5，∠PAP'＝60°，∴△APP'是等边三角形，∴PP'＝AP＝5，∠APP'＝60°，∵∠APB＝150°，∴∠BPP'＝∠APB﹣∠APP'＝90根据勾股定理得，BP'=√BP2+PP′2=13，∴CP＝13，拓展廷伸：①如图4，在△ABC中，∠ABC＝90°，AB＝BC，将△ABD绕点B顺时针旋转90°得到△BCD'，∴BD'＝BD，CD'＝AD，∠BCD'＝∠BAD，∵∠ABC＝∠ADC＝90°，∴∠BAD+∠BCD＝180°，∴∠BCD+∠BCD'＝180°，∴点D'在DC的延长线上，∴DD'＝CD+CD'＝CD+AD，在Rt△DBD'中，DD'=√2BD，∴√2BD＝CD+AD；②如图5，在△ABC中，∠ABC＝90°，AB＝BC，将△CBD绕点B顺时针旋转90°得到△ABD'，∴BD'＝BD，CD＝AD'，∠DBD'＝90°，∠BCD＝∠BAD'，AB与CD的交点记作G，∵∠ADC＝∠ABC＝90°，∴∠DAB+∠AGD＝∠BCD+∠BGC＝180°，∵∠AGD＝∠BGC，∴∠BAD＝∠BCD，∴∠BAD＝∠BAD'，∴点D'在AD的延长线上，∴DD'＝AD'﹣AD＝CD﹣AD＝2，在Rt△BDD'中，BD=√22DD'=√2．【练1】如图，在等边△ABC中，点D为△ABC内的一点，∠ADB＝120°，∠ADC＝90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．（1）求证：AD＝DE；（2）求∠DCE的度数；（3）若BD＝1，求AD，CD的长．【答案】（1）见解析（2）90°（3）√3【解析】（1）证明：∵将△ABD绕点A逆时针旋转60°得△ACE∴△ABD≌△ACE，∠BAC＝∠DAE，∴AD＝AE，BD＝CE，∠AEC＝∠ADB＝120°，∵△ABC为等边三角形∴∠BAC＝60°∴∠DAE＝60°∴△ADE为等边三角形，∴AD＝DE，（2）∠ADC＝90°，∠AEC＝120°，∠DAE＝60°∴∠DCE＝360°﹣∠ADC﹣∠AEC﹣∠DAE＝90°，（3）∵△ADE为等边三角形∴∠ADE＝60°∴∠CDE＝∠ADC﹣∠ADE＝30°又∵∠DCE＝90°∴DE＝2CE＝2BD＝2，∴AD＝DE＝2在Rt△DCE中，DC=√DE2−CE2=√22−12=√3．【练2】如图，四边形ABCD中，∠ABC＝∠ADC＝45°，将△BCD绕点C顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到△ACE．（1）请求出旋转角的度数；（2）请判断AE与BD的位置关系，并说明理由；（3）若AD＝2，CD＝3，试求出四边形ABCD的对角线BD的长．【答案】（1）90°（2）证明见解析（3）BD=√22【解析】解：（1）∵将△BCD绕点C顺时针旋转得到△ACE ∴△BCD'≌△ACE∴AC＝BC，又∵∠ABC＝45°，∴∠ABC＝∠BAC＝45°∴∠ACB＝90°故旋转角的度数为90°（2）AE⊥BD．理由如下：在Rt△BCM中，∠BCM＝90°∴∠MBC+∠BMC＝90°∵△BCD'≌△ACE∴∠DBC＝∠EAC即∠MBC＝∠NAM又∵∠BMC＝∠AMN∴∠AMN+∠CAE＝90°∴∠AND＝90°∴AE⊥BD（3）如图，连接DE，由旋转图形的性质可知CD＝CE，BD＝AE，旋转角∠DCE＝90°∴∠EDC＝∠CED＝45°∵CD＝3，∴CE＝3在Rt△DCE中，∠DCE＝90°∴DE=√CD2+CE2=√9+9=3√2∵∠ADC＝45°∴∠ADE＝∠ADC+∠EDC＝90°在Rt△ADE中，∠ADE＝90°∴EA=√AD2+DE2=√18+4=√22∴BD=√22【练3】如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC＞AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC＝EB，∵AD ＝AE，∠DAE＝60°，∴△ADE是等边三角形，∴AD＝DE．在△DBE中，BD+EB＞DE，即：BD+DC＞AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC＞√2AD．（2）如果点D运动到等腰直角三角形△ABC外或内时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．创新应用：（3）已知：如图4，等腰△ABC中，AB＝AC，且∠BAC＝α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC＝180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．【答案】（1）证明见解析（2）BD+DC≥√2AD；（3）猜想：BD+DC＜2AD；证明见解析【解析】解：（1）证明：把△ACD绕点A顺时针旋转90°得到△ABE，连接ED则有△ACD≌△ABE，DC＝EB∵AD＝AE，∠DAE＝90°∴△ADE是等腰直角三角形∴DE=√2AD在△DBE中，BD+EB＞DE，即：BD+DC＞√2AD；（2）把△ABD旋转，使AB与AC AC旋转，得到△ACD′，则BD＝CD′，在△CDD′中，CD+CD′＞DD′，即BD+CD＞DD′，∵△ADD′是钝角三角形，则DD′＞√2AD当D运动到B的位置时，DD′＝BC=√2AD．∴BD+DC≥√2AD；（3）猜想1：BD+DC＜2AD证明：把△ACD绕点A顺时针旋转α，得到△ABE则有△ACD≌△ABE，DC＝EB，∠ACD＝∠ABE∵∠BAC+∠BDC＝180°∴∠ABD+∠ACD＝180°∴∠ABD+∠ABE＝180°即：E、B、D三点共线．∴在△ADE中，AE+AD＞ED，即BD+DC＜2AD．【题型三：旋转与相似三角形的构造】【例】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，给出下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S△ABF：S四边形CDEF＝2：5，其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】D【解析】解：如图，过D作DM∥BE交AC于N，∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝90°，AD＝BC，∵BE⊥AC于点F，∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90°，∴△AEF∽△CAB，故①正确；∴△AEF ∽△CBF ，∴AE BC ＝AF CF ，∵AE ＝12AD ＝12BC ，∴AF CF ＝12，∴CF ＝2AF ，故②正确，∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM ＝DE ＝12BC ，∴BM ＝CM ，∴CN ＝NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF ＝DC ，故③正确；∵△AEF ∽△CBF ，∴EF BF ＝AE BC ＝12，∴S △AEF ＝12S △ABF ，S △ABF ＝16S 矩形ABCD ，∴S △AEF ＝112S 矩形ABCD ，又∵S 四边形CDEF ＝S △ACD ﹣S △AEF ＝12S 矩形ABCD ﹣112S 矩形ABCD ＝512S 矩形ABCD ，∴S △ABF ：S 四边形CDEF ＝2：5，故④正确；【练1】如图，正方形ABCD 的边长为8，线段CE 绕着点C 逆时针方向旋转，且CE =3，连接BE ，以BE 为边作正方形BEFG ，M 为AB FM 的长最小时，tan ∠ECB =______．【答案】13【解析】解：连接BD ，BF ，FD ，如图，∵BD BC =BF BE =√2，∴BD BF =BC BE ，∵∠FBD+∠DBE=45°，∠EBC+∠DBE=45°，∴∠FBD=∠EBC，∴△EBC∽△FBD，∴∠FDB=∠ECB，DFCE =BDBC=√2，∴DF=√2CE=3√2，由题意知：FM、DF、DM三条线段满足FM+DF≥MD，其中DM、DF的值一定，∴当M，F，D三点一线时，FM最小，过点M作MN⊥BD，垂足为G，∵∠MBN=45°，BM=12AB=4，∴MN=BN=2√2，∵MD=√AM2+AD2=√42+82=4√5，∴DG=√MD2−MG2=√(4√5)2−(2√2)2=6√2，∴tan∠ECB=tan∠FDG=MGDG =√26√2=13，故答案为：13．【练2】如图，在△ABC中，AB＝5，D为边AB上－动点，以CD为一边作正方形CDEF，当点D从点B运动到点A时，点E运动的路径长为_________．【答案】5√2【解析】解：如图，作GB⊥BC于B，取GB=BC，当点D与点B重合时，则点E与点G重合，∴∠CBG=90°，∴CG=√2BC，∠GCB=45°，∵四边形CDEF是正方形，∴CE=√2DC，∠ECD=45°，∴∠BCD+∠DCG =∠GCE+∠DCG =45°，∴∠BCD =∠GCE，且CGBC =CEDC=√2，∴△CGE∽△CBD，∴GEBD =CEDC=√2，即GE=√2BD，∵BD=5，∴点E运动的路径长为GE=√2BD=5√2．【练3】在△ABC和△ADE中，BA=BC，DA=DE，且∠ABC=∠ADE=α，点E在△ABC的内部，连接EC，EB，EA和BD，并且∠ACE+∠ABE=90°．（观察猜想）（1）如图①，当α=60°时，线段BD与CE的数量关系为__________，线段EA，EB，EC的数量关系为__________．（探究证明）（2）如图②，当α=90°时，（1）中的结论是否依然成立？若成立，请给出证明，若不成立，请说明理由；（拓展应用）（3）在（2）的条件下，当点E在线段CD上时，若BC=2√5，请直接写出△BDE的面积．【答案】（1）BD=CE，EB2+EC2=EA2；（2）不成立，理由见解析；（3）2【解析】（1）如图①中，∵BA=BC，DA=DE．且∠ABC=∠ADE=60°，∴△ABC，△ADE都是等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，∴∠DAB=∠EAC，∴△DAB≌△EAC（SAS），∴BD=EC，∠ABD=∠ACE，∵∠ACE+∠ABE=90°，∴∠ABD+∠ABE=90°，∴∠DBE=90°，∴DE2=BD2+BE2，∵EA=DE，BD=EC，∴EA2=BE2+EC2．故答案为：BD=EC，EA2=EB2+EC2．（2）结论：EA2=EC2+2BE2．理由：如图②中，∵BA =BC ，DA =DE ．且∠ABC =∠ADE =90°， ∴△ABC ，△ADE 都是等腰直角三角形， ∴∠DAE =∠BAC =45°，∴∠DAB =∠EAC ， ∵AD AE =√22，AB AC =√22， ∴AD AE =ABAC ，∴△DAB ∽△EAC ，∴DB EC =AB AC =√22，∠ACE =∠ABD ， ∵∠ACE +∠ABE =90°，∴∠ABD +∠ABE =90°，∴∠DBE =90°，∴DE 2=BD 2+BE 2，∵EA =√2DE ，BD =√22EC ， ∴12EA 2=12EC 2+BE 2，∴EA 2=EC 2+2BE 2．（3）如图③中，∵∠AED =45°，D ，E ，C 共线， ∴∠AEC =135°，∵△ADB ∽△AEC ，∴∠ADB =∠AEC =135°，∵∠ADE =∠DBE =90°，∴∠BDE =∠BED =45°，∴BD =BE ，∴DE =√2BD ，∵EC =√2BD ，∴AD =DE =EC ，设AD =DE =EC =x ，在Rt△ABC中，∵AB=BC=2√5，∴AC=2√10，在Rt△ADC中，∵AD2+DC2=AC2，∴x2+4x2=40，∴x=2√2（负根已经舍弃），∴AD=DE=2√2，∴BD=BE=2，×2×2=2．∴S△BDE=12。

【最新整理，下载后即可编辑】旋转模型专题一、等线段共点二、按图形分类1、等腰三角形，2、等边三角形，3、等腰直角三角形，4、正方形三、按模型分类1、手拉手模型2、角含半角模型3、对角互补模型4、与勾股定理结合5、费马点问题 例题精讲 一、手拉手模型等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形M DNEC B FAA BCD1、已知：如图，点C为线段AB上一点，ACM∆、CBN∆是等边三角形．常见结论：（1）AN BM=（2）CD CE=（3）CF平分AFB∠（4）CDE△是等边三角形．（5）∠AFM=60°且保持不变2、如图，在凸四边形ABCD中，30BCD∠=︒,60DAB AD AB∠=︒=，．求证：222AC CD BC=+3、已知ABC∆，以AC为边在ABC∆外作等腰ACD∆，其中AC AD=。

⑴如图①，若2DAC ABC∠=∠，AC BC=，四边形ABCD是平行四边形，则_____ABC∠=⑵如图②，若30ABC∠=︒，ACD∆是等边三角形，3AB=，4BC=，求BD 的长；⑶如图③，若ACD∠为锐角，作AH BC⊥于H，当2224BD AH BC=+时，2DAC ABC ∠=∠是否成立？若不成立，请说明你的理由；若成立，证明你的结论。

③②①AH CBDDCBADCBA二、角含半角模型4、已知：如图1在Rt ABC ∆中，90BAC ∠=︒，AB AC =，点D 、E 分别为线段BC 上两动点，若45DAE ∠=︒．探究线段BD 、DE 、EC 三条线段之间的数量关系．小明的思路是：把AEC ∆绕点A 顺时针旋转90︒，得到ABE '∆，连结E D '，使问题得到解决．请你参考小明的思路探究并解决下列问题： ⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式，并对你的猜想给予证明；⑵ 当动点E 在线段BC 上，动点D 运动在线段CB 延长线上时，如图2，其它条件不变，⑴中探究的结论是否发生改变？说明你的猜想并给予证明．5、在正方形ABCD 中，点E 、F 分别在边BC 、CD 上，且∠EAF=∠CEF=45°，（1）将△ADF 绕着点A 顺时针旋转90°，得到△ABG ，如图1， 求证：△AEG ≌△AEF ；（2）若直线EF 与AB 、AD 的延长线分别交于点M,N ，如图2， 求证：222NF ME EF +=图1ABCDE图2AB CDE（3）将正方形改为长与宽不相等的矩形，若其余条件不变，请你直接写出线段EF ，BE ，DF 之间的数量关系。

9．将一副三角尺（在 Rt△ABC 中，∠ACB＝90°，∠B＝60°；在 Rt△DEF 中，∠EDF＝90°，∠E＝45°）如图① 摆放，点 D 为 AB 的中点，DE 交 AC 于点 P，DF 经过点 C．将△DEF 绕点 D 顺时针方向旋转角 α（0°＜α＜
PM 60°），DE′交 AC 于点 M，DF′交 BC 于点 N，则 ＝________．
如图③， VABC 中， BAC 30 ， ACB 90 ，对 VABC 作变换 , n 得△ABC ，使点 B 、 C 、 C 在同
一直线上，且四边形 ABBC 为矩形，请直接写出 n 的值．
（1）求点 P 到 AB 的最大距离； （2）当点 P 在 AC 上运动时， ①求 tan PDE 的值；
②把△ PDE 绕点 E 顺时针方向旋转，当点 P 的对应点 P' 落在 ED 上时， ED 的对应线段 ED ' 恰好与 AB 垂直，
求此时 t 的值． （3）当点 P 关于直线 DE 的对称点为 F 时，四边形 PEFD 能否成为菱形？若能，直接写出 t 的值；若不能， 请说明理由． 15．发现规律 （1）如图①，△ABC 与△ADE 都是等边三角形，直线 BD，CE 交于点 F．直线 BD，AC 交于点 H．求∠BFC 的度数．
常数），则 BD 的长为____．（用含 k 的式子表示）
7．如图，在△ABC 中，AB＝5，D 为边 AB 上－动点，以 CD 为一边作正方形 CDEF，当点 D 从点 B 运动 到点 A 时，点 E 运动的路径长为_________．
8．已知正方形 DEFG 的顶点 F 在正方形 ABCD 的一边 AD 的延长线上，连结 AG，CE 交于点 H，若 AB 3 ， DE 2 ，则 CH 的长为________.

初中数学旋转的六大模型,初中几何旋转经典例题标题：初中数学旋转的六创作者，初中几何旋转经典例题在初中的数学学习中，旋转是一个重要的概念，它不仅在几何学中占据着核心地位，还在代数学、统计学等其他领域有着广泛的应用。

本文将详细介绍初中数学旋转的六创作者，并通过经典例题来深化理解。

旋转是指一个图形绕着某一点转动一定的角度。

在这个过程中，图形上任意一点所经过的路径形成一个圆，这个圆叫做旋转圆，点叫做旋转中心。

旋转的角度一般用角度或者弧度来表示。

中心对称旋转：图形以旋转中心为对称中心，旋转角度为偶数倍的180度。

绕固定点旋转：图形围绕一个固定点旋转，这个固定点称为旋转中心。

旋转对称图形：图形可以通过旋转得到，这种图形称为旋转对称图形。

旋转角相等：如果两个图形可以通过旋转互相得到，那么它们的旋转角必然相等。

旋转角互补：如果两个图形的一条边和另一条边的延长线组成一个平角，那么这两个图形的旋转角互补。

旋转改变形状：旋转可以改变图形的形状，但不会改变图形的面积。

例1：在正方形ABCD中，E是BC的中点，F是AC上一点，且CF=2AF。

求证：EF平分∠AEB。

证明：我们可以通过旋转证明。

把△ABE绕B点按逆时针方向旋转60°，得到△CBG，则BG//AE，所以∠FGB=∠FEA。

因为CF=2AF，所以FG=2FE。

所以可以得出∠FEB=∠FGB+∠GBF=∠FEA+∠AEB+∠ABE=∠FEA+∠AEB+∠EAB=180°即∠FEA+∠AEB=180°-∠EAB=∠BEF所以∠BEF = ∠FEA即 EF平分∠AEB。

例2：在Rt△ABC中，∠C=90°，D是AB的中点，E、F分别在AC和BC上，且DE⊥DF。

求证：EF^2=AE^2+BF^2。

证明：把Rt△ABC绕D点按顺时针方向旋转90°得到Rt△AB’C’，则可知：△ABC≌△AB’C’，所以可知DE=DF，因为DE⊥DF，所以可知四边形DECF’是正方形。

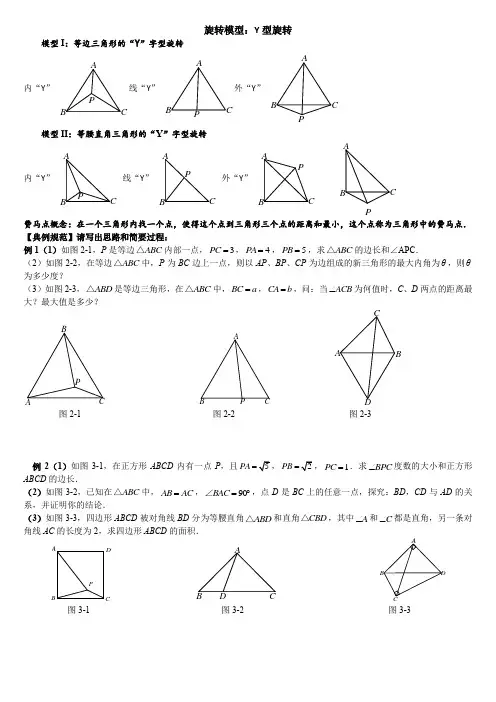
旋转模型：Y 型旋转模型I ：等边三角形的“Y ”字型旋转内“Y ”线“Y ”外“Y ”模型II ：等腰直角三角形的“Y ”字型旋转内“Y ”线“Y ”外“Y ”P费马点概念：在一个三角形内找一个点，使得这个点到三角形三个点的距离和最小，这个点称为三角形中的费马点． 【典例规范】请写出思路和简要过程：例1（1）如图2-1，P 是等边ABC △内部一点，3PC =，4PA =，5PB =，求ABC △的边长和∠APC ．（2）如图2-2，在等边ABC △中，P 为BC 边上一点，则以AP 、BP 、CP 为边组成的新三角形的最大内角为θ，则θ为多少度？（3）如图2-3，ABD △是等边三角形，在ABC △中，BC a =，CA b =，问：当ACB ∠为何值时，C 、D 两点的距离最大？最大值是多少？AB C PABPCAC BD图2-1 图2-2 图2-3例2（1）如图3-1，在正方形ABCD 内有一点P ，且PA =PB 1PC =．求BPC ∠度数的大小和正方形ABCD 的边长．（2）如图3-2，已知在ABC △中，AB AC =，90BAC =︒∠，点D 是BC 上的任意一点，探究：BD ，CD 与AD 的关系，并证明你的结论．（3）如图3-3，四边形ABCD 被对角线BD 分为等腰直角ABD △和直角CBD △，其中A ∠和C ∠都是直角，另一条对角线AC 的长度为2，求四边形ABCD 的面积．ABD AB C D图3-1 图3-2 图3-3PDC BA例3如果△ABC 的三个内角均小于120°,是否存在一点P ，使其与这个三角形的三个顶点的距离之和（即PA+PB+PC ）为最小,如果存在，请写出点P 的具体位置。

A BC P【举一反三自主练习】请写出思路和简要过程：1. (1) 如图，P 是等边ABC △内部一点 ，PC =1，PA =√3，PB =2，求∠APC 和∠BPC 和∠APC ． (2) 如图，P 是等边ABC △内部一点 ，PC =1，PA =1，PB =√2，求∠BPC ．（3）如图，在等边ABC △中，P 为BC 边上一点，则以AP 、BP 、CP 为边组成的新三角形的最大内角为θ，则θ为多少度？AB C PABC PABPC2.（1）如图，四边形ABPC 中，AP ，BC 是对角线，△ABC 是等边三角形．∠BPC=120°，PC=2，PB=4．求PA 的长.（2）如图，四边形ABPC 中，AP ，BC 是对角线，△ABC 是等腰三角形且∠BAC=120°．∠BPC=60°，PC=4，PB=2．求PA 的长.（3）如图，四边形ABCD 中，AP ，BC 是对角线，△ADC 是等腰直角三角形且∠BDC=90°，∠BAC=90°，AB=4，AC=2．求AD 的长.（4）如图，四边形ABCD 中，AP ，BC 是对角线，△ADC 是等腰直角三角形且∠BDC=90°，∠BAC=90°，AB=4，AC=2．求AD 的长.（5）如图，四边形ABPC 中，AP ，BC 是对角线，△ABC 是等边三角形．∠BPC=30°，PC=3，PB=4．求PA 的长.3.（1）如图，正方形ABCD 的对角线交于点O ，以AD 为边向外作Rt ADE △，90AED ∠=︒，连接OE ，6DE =，OE =求AE 的长= ． （2）如图，以Rt ABC △的斜边BC 为一边在ABC △同侧作正方形BCEF，设正方形的中心为O ，连接AO ，如果4AB =，AO =AC 的长=．（3）如图，ABC △为等边三角形，以AB 为对角线作矩形ADBE ，点E 在ABC △内部，连接EC ，若150BEC =︒∠，1EC =，则ABC △的边长为____ ___．（4）已知：PA =4PB =，以AB 为一边作正方形ABCD ，使P 、D 两点落在直线AB 的两侧．当45APB ∠=︒时，求AB = ，PD 的长= ．AEB CD OB FC AOEPDABC4.背景资料：在已知△ABC 所在平面上求一点P ，使它到三角形的三个顶点的距离之和最小．这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”． 如图①，当△ABC 三个内角均小于120°时，费马点P 在△ABC 内部，此时∠APB =∠BPC =∠CP A =120°，此时，P A +PB +PC 的值最小．解决问题：（1）如图②，等边△ABC 内有一点P ，若点P 到顶点A 、B 、C 的距离分别为3，4，5，求∠APB 的度数． 为了解决本题，我们可以将△ABP 绕顶点A 旋转到△ACP ′处，此时△ACP ′≌△ABP ，这样就可以利用旋转变换，将三条线段P A ，PB ，PC 转化到一个三角形中，从而求出∠APB =（2）请你利用第（1）题的解答思想方法，解答下面问题：如图③，在Rt △ABC 中，∠C =90°，AC =1，∠ABC =30°，点P 为Rt △ABC 的费马点，连接AP ，BP ，CP ，求P A +PB +PC 的值．拓展应用（3）①如图④，△ABC 三个内角均小于120°，在△ABC 外侧作等边三角形ACB '，连接BB '.求证：BB '过△ABC 的费马点P ，且BB '=P A +PB +PC .②已知三村庄A ，B ，C 构成了如图⑤所示的△ABC （其中∠A ，∠C 均小于120°），AB =3 km ，BC =4 km ，∠B =30°，现选取一点P 打水井，使水井P 到三村庄A ，B ，C 所铺设的输水管总长度最小. 求输水管总长度的最小值.5.如图，四边形ABCD 是正方形，ABE △是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60︒得到BN ，连接EN 、AM 、CM ． （1）求证：AMB ENB △≌△；（2）①当M 点在何处时，AM CM +的值最小；②当M 点在何处时，AM BM CM ++的值最小，并说明理由； （3）当AM BM CM ++1+时，求正方形的边长．ENM BCDA。

范文范例学习参考几何变换的三种模型手拉手、半角、对角互补「等腰三角形手拉手模型1等腰直角三角形（包含正方形）、等边三角形（包含费马点）i 特殊角《对角互补模型W厂般角产线段变换（与圆相关）在 4ABC 中，AB=AC , /BAC =支（0口<ot<60口）,将线段 BC绕点B 逆时针旋转60。

得到线段BD .（1）如图1,直接写出/ABD 的大小（用含口的式子表示）；（2）如图2, /BCE=150〉,/ABE=60©,判断△ ABE 的形状并加以证明; （3）在（2）的条件下，连结 DE ,若NDEC =45°,求a 的值.角含半角模型件寺殊角:一般角旋转变换 真题演练【练1】（2013北京中考）范文范例学习参考【练2】（2012年北京中考）在4ABC中，BA = BC , /BAC =口，M 是AC的中点，P是线段上的动点，将线段PA绕点P顺时针旋转力得到线段PQ.（1）若a印且点P与点M重合（如图1）,线段CQ的延长线交射线BM于点D , 请补全图形，并写出/CDB的度数；S1（2）在图2中，点P不与点B , M重合，线段CQ的延长线与射线BM交于点D ,猜想/CDB的大小（用含豆的代数式表示），并加以证明；（3）对于适当大小的a ,当点P在线段BM上运动到某一位置（不与点B , M重合）时，能使得线段CQ的延长线与射线BM交于点D ,且PQ=QD ,请直接写出a的范围.范文范例学习参考例题精讲考点1：手拉手模型：全等和相似包含：等腰三角形、等腰直角三角形（正方形）、等边三角形伴随旋转出全等，处于各种位置的旋转模型，及残缺的旋转模型都要能很快看出来（1）等腰三角形旋转模型图（共顶点旋转等腰出伴随全等）（2）等边三角形旋转模型图（共顶点旋转等边出伴随全等）（3）等腰直角旋转模型图（共顶点旋转等腰直角出伴随全等）（4）不等边旋转模型图（共顶点旋转不等腰出伴随相似）【例1】(14年海淀期末)已知四边形ABCD和四边形CEFG都是正方形，且AB>CE .(1)如图1 ,连接BG、DG .求证：BG =DE ;(2)如图2,如果正方形ABCD的边长为近,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG // BD , BG = BD .①求ZBDE的度数；②请直接写出正方形CEFG的边长的值.【例2】(2014年西城一模) 四边形ABCD是正方形，ABEF是等腰直角三角形，ZBEF =90°, BE =EF ,连接DF , G 为DF 的中点，连接EG, CG , EC。

专题一旋转中的几何模型模型一　“手拉手”模型模型特征：两个等边三角形或等腰直角三角形或正方形共顶点．模型说明：如图1，△ABE，△ACF都是等边三角形，可证△AEC≌△ABF.如图2，△ABD，△ACE都是等腰直角三角形，可证△ADC≌△ABE.如图3，四边形ABEF，四边形ACHD都是正方形，可证△ABD≌△AFC.图1 图2 图3等腰图形有旋转，辩清共点旋转边，关注三边旋转角，全等思考边角边。

1【问题提出】(1)如图①，△ABC,△ADE均为等边三角形，点D,E分别在边AB，AC上．将△ADE绕点A沿顺时针方向旋转，连结BD,CE．在图②中证明△ADB≅△AEC．[学以致用](2)在(1)的条件下，当点D,E,C在同一条直线上时，∠EDB的大小为度．[拓展延伸](3)在(1)的条件下，连结CD．若BC=6,AD=4直接写出△DBC的面积S的取值范围．【思路点拨】(1)根据“手拉手”模型，证明△ADB≅△AEC即可；(2)分“当点E在线段CD上”和“当点E在线段CD的延长线上”两种情况，再根据“手拉手”模型中的结论即可求得∠EDB的大小；(3)分别求出△DBC的面积最大值和最小值即可得到结论【详解】(1)∵ABC,ADE均为等边三角形，∴AD=AE，AB=AC，∴∠DAE-∠BAE=∠BAC-∠BAE，即∠BAD=∠CAE在△ADB和△AEC中，AD=AE∠BAD=∠CAE AB=AC∴ABD ≅ACE (SAS )；(2)当D ,E ,C 在同一条直线上时，分两种情况：①当点E 在线段CD 上时，如图，∵△ADE 是等边三角形，∴∠ADE =∠AED =60°，∴∠AEC =180°-∠AED =120°，由(1)可知，△ADB ≅△AEC ，∴∠ADB =∠AEC =120°，∴∠EDB =∠ADB -∠ADE =120°-60°=60°②当点E 在线段CD 的延长线上时，如图，∵△ADE 是等边三角形，∴∠ADE =∠AED =60°∴∠ADC =180°-∠ADE =120°，由(1)可知，△ADB ≅△AEC∴∠ADB =∠AEC =60°，∴∠EDB =∠ADB +∠ADE =60°+60°=120°综上所述，∠EDB 的大小为60°或120°(3)过点A 作AF ⊥BC 于点F ，当点D 在线段AF 上时，点D 到BC 的距离最短，此时，点D 到BC 的距离为线段DF 的长，如图：∵ΔABC 是等边三角形，AF ⊥BC ，BC =6∴AB =BC =6，BF =12BC =3∴AF =AB 2-BF 2=62-32=33∴DF =33-4此时S .DBC =12BC ⋅DF =12×6×(33-4)=93-12；当D 在线段FA 的延长线上时，点D 到BC 的距离最大，此时点D 到BC 的距离为线段DF 的长，如图，∵ΔABC 是等边三角形，AF ⊥BC ，BC =6∴AB =BC =6，BF =12BC =3，∴AF =AB 2-BF 2=62-32=33∵AD =4∴DF =AF +AD =33+4此时，S .DBC =12BC ⋅DF =12×6×(33+4)=93+12；综上所述，△DBC 的面积S 取值是93-12≤5≤93+12【点评】 利用“手拉手”模型，构造对应边“拉手线”组成的两个三角形全等是解题关键2已知正方形ABCD 和等腰直角三角形BEF ，BE =EF ，∠BEF =90°，按图1放置，使点F 在BC 上，取DF 的中点G ，连接EG ，CG ．(1)探索EG，CG的数量关系和位置关系并证明；(2)将图(1)中△BEF绕点B顺时针旋转45°，再连接DF，取DF中点G(见图2)，(1)中的结论是否仍然成立？证明你的结论；(3)将图(1)中△BEF绕点B顺时针转动任意角度(旋转角在0°到90°之间)，再连接DF，取DF中点G(见图3)，(1)中的结论是否仍然成立？证明你的结论．【思路点拨】(1)首先证明B、E、D三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=DG= GF=CG，得到∠EGF=2∠EDG，∠CGF=2∠CDG，从而证得∠EGC=90°；(2)首先证明△FEG≌△DHG，然后证明△ECH为等腰直角三角形．可以证得：EG=CG且EG⊥CG；(3)首先证明：△BEC≌△FEH，即可证得：△ECH为等腰直角三角形，从而得到：EG=CG且EG⊥CG．【解题过程】解：(1)EG=CG且EG⊥CG．证明如下：如图①，连接BD．∵正方形ABCD和等腰Rt△BEF，∴∠EBF=∠DBC=45°．∴B、E、D三点共线．∵∠DEF=90°，G为DF的中点，∠DCB=90°，∴EG=DG=GF=CG．∴∠EGF=2∠EDG，∠CGF=2∠CDG．∴∠EGF+∠CGF=2∠EDC=90°，即∠EGC=90°，∴EG⊥CG．(2)仍然成立，证明如下：如图②，延长EG交CD于点H．∵BE⊥EF，∴EF∥CD，∴∠1=∠2．又∵∠3=∠4，FG=DG，∴△FEG≌△DHG，∴EF=DH，EG=GH．∵△BEF为等腰直角三角形，∴BE=EF，∴BE=DH．∵CD=BC，∴CE=CH．∴△ECH为等腰直角三角形．又∵EG=GH，∴EG=CG且EG⊥CG(3)仍然成立．证明如下：如图③，延长CG至H，使GH=CG，连接HF交BC于M，连接EH、EC．∵GF=GD，∠HGF=∠CGD，HG=CG，∴△HFG≌△CDG，∴HF=CD，∠GHF=∠GCD，∴HF∥CD．∵正方形ABCD，∴HF=BC，HF⊥BC．∵△BEF是等腰直角三角形，∴BE=EF，∠EBC=∠HFE，∴△BEC≌△FEH，∴HE=EC，∠BEC=∠FEH，∴∠BEF=∠HEC=90°，∴△ECH为等腰直角三角形．又∵CG=GH，∴EG=CG且EG⊥CG．针对训练11已知ΔABC是等边三角形，AD⊥BC于点D，点E是直线AD上的动点，将BE绕点B顺时针方向旋转60°得到BF，连接EF，CF，AF．(1)问题发现：如图1，当点E在线段AD上时，且∠AFC=35°，则∠FAC的度数是；(2)结论证明：如图2，当点E 在线段AD 的延长线上时，请判断∠AFC 和∠FAC 的数量关系，并证明你的结论；(3)拓展延伸：若点E 在直线AD 上运动，若存在一个位置，使得ΔACF 是等腰直角三角形，请直接写出此时∠EBC 的度数．【答案】(1)55°；(2)∠AFC +∠FAC =90°，见解析；(3)15°或75°【解析】(1)55°，理由：∵ΔABC 是等边三角形，∴AB =AC =BC ，∠ABC =∠BAC =∠ACB =60°，∵AB =AC ，AD ⊥BC ，∴∠BAD =30°，∵将BE 绕点B 顺时针方向旋转60°得到BF ，∴BE =BF ，∠EBF =60°，∴∠EBF =∠ABC ，在△ADC 和△BDA 中，AB =BC∠ABE =∠FBC BE =BF，∴ΔABE ≌ΔCBF SAS ，∴∠BAE =∠BCF =30°，∴∠ACF =90°，∴∠AFC +∠FAC =90°；∵∠AFC =35°，∴∠FAC =55°；(2)结论：∠AFC +∠FAC =90°，理由如下：∵ΔABC 是等边三角形，∴AB =AC =BC ，∠ABC =∠BAC =∠ACB =60°，∵AB =AC ，AD ⊥BC ，∴∠BAD =30°，∵将BE 绕点B 顺时针方向旋转60°得到BF ，∴BE =BF ，∠EBF =60°，∴∠EBF =∠ABC ，在△ADC 和△BDA 中，AB =BC∠ABE =∠FBC BE =BF，∴ΔABE ≌ΔCBF SAS ，∴∠BAE =∠BCF =30°，∴∠ACF =90°，∴∠AFC +∠FAC =90°；(3)∠EBC =15°或75°分两种情况：①点E 在点A 的下方时，如图：∵ΔACF 是等腰直角三角形，∴AC =CF ，由(2)得ΔABE ≌ΔCBF ，∴CF =AE ，∴AC =AE =AB ，∴∠ABE =180°-30°2=75°，∴∠EBC =∠ABE -∠ABC =75°-60°=15°；②点E 在和点A 的上方时，如图：同理可得∠EBC =∠ABE +∠ABC =75°．2已知四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转α(0°<α<90°)，得到线段CE ，联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F ．(1)如图，当BE =CE 时，求旋转角α的度数；(2)当旋转角α的大小发生变化时，∠BEF 的度数是否发生变化?如果变化，请用含α的代数式表示；如果不变，请求出∠BEF 的度数；(3)联结AF ，求证：DE =2AF ．【答案】(1)30°；(2)不变；45°；(3)见解析【解析】(1)证明：在正方形ABCD 中, BC =CD .由旋转知，CE=CD,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形，∴∠BCE=60°.又∵∠BCD=90°,∴α=∠DCE=30°.(2)∠BEF的度数不发生变化.在△CED中，CE=CD,∴∠CED=∠CDE=180°-α2=90°-α2，在△CEB中,CE=CB,∠BCE=90°-α,∴∠CEB=∠CBE=180°-∠BCE2=45°+α2,∴∠BEF=180°-∠CED-∠CEB=45°.(3)过点A作AG∥DF与BF的延长线交于点G，过点A作AH∥GF与DF交于点H，过点C作CI⊥DF于点I易知四边形AGFH是平行四边形，又∵BF⊥DF，∴平行四边形AGFH是矩形.∵∠BAD=∠BGF=90°，∠BPF=∠APD，∴∠ABG=∠ADH.又∵∠AGB=∠AHD=90°，AB=AD，∴△ABG≌△ADH.∴AG=AH，∴矩形AGFH是正方形.∴∠AFH=∠FAH=45°，∴AH=AF∵∠DAH+∠ADH=∠CDI+∠ADH=90°∴∠DAH=∠CDI又∵∠AHD=∠DIC=90°，AD=DC，∴△AHD≌△DIC∴AH=DI，∵DE=2DI，∴DE=2AH=2AF模型二　对角互补模型对角互补模型的特征：外观呈现四边形，且对角和为180°。

【专题12】几何图形的旋转模型研究【回归概念】旋转变换是由一个图形改变为另一个图形，在改变过程中，原图上所有的点都绕一个固定的点换同一方向，转动同一个角度。

旋转模型主要体现在以下几个情况:【规律探寻】1.共顶点旋转模型(证明基本思想“SAS”)2.利用旋转思想构造辅助线（1）根据相等的边先找出被旋转的三角形（2）根据对应边找出旋转角度（3）根据旋转角度画出对应的旋转的三角形3.旋转变换前后具有以下性质：（1）对应线段相等，对应角相等（2）对应点位置的排列次序相同（3）任意两条对应线段所在直线的夹角都等于旋转角 ．4.旋转变换还用于处理：①几何最值问题：几何最值两个重要公理依据是：两点之间线段最短和垂线段最短；②有关线段的不等关系；③自己构造绕某点旋转某角度（特别是60度），把共顶点的几条线段变为首尾相接的几条线段，再变为共线取得最小值问题，计算中常用到等腰三角形或勾股定理等知识。

【典例解析】【例题1】（2019•湖北省随州市•3分）如图，在平面直角坐标系中，Rt△ABC的直角顶点C的坐标为（1，0），点A在x轴正半轴上，且AC=2．将△ABC先绕点C逆时针旋转90°，再向左平移3个单位，则变换后点A的对应点的坐标为______．【例题2】（2019•浙江绍兴•12分）如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10．（1）在旋转过程中，①当A，D，M三点在同一直线上时，求AM的长．②当A，D，M三点为同一直角三角形的顶点时，求AM的长．（2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2，此时∠AD2C＝135°，CD2＝60，求BD2的长．【例题3】（2018•自贡）如图，已知∠AOB=60°，在∠AOB的平分线OM上有一点C，将一个120°角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E．（1）当∠DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；（2）当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；（3）当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．【达标检测】1. （2018海南）（3.00分）如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（）A．6 B．8 C．10 D．122. （2017山东泰安）如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为（）A．30°B．60° C．90° D．120°3. （2019•湖北省荆门市•3分）如图，Rt△OCB的斜边在y轴上，OC＝3，含30°角的顶点与原点重合，直角顶点C在第二象限，将Rt△OCB绕原点顺时针旋转120°后得到△OC′B'，则B点的对应点B′的坐标是（）A3，﹣1）B．（13）C．（2，0）D3，0）4. 如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF 中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（）A．5 B．4 C． D．5.（2019浙江丽水3分）将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则的值是（）A．522B．2﹣1 C．D．226. (2019•湖南常德•3分)如图，已知△ABC是等腰三角形，AB＝AC，∠BAC＝45°，点D在AC边上，将△ABD绕点A逆时针旋转45°得到△ACD′，且点D′、D、B三点在同一条直线上，则∠ABD的度数是．7. (2019•湖南益阳•4分)在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，使各顶点仍在格点上，则其旋转角的度数是．8. （2019•海南省•4分）如图，将Rt△ABC的斜边AB绕点A顺时针旋转α（0°＜α＜90°）得到AE，直角边AC绕点A逆时针旋转β（0°＜β＜90°）得到AF，连结EF．若AB＝3，AC＝2，且α+β＝∠B，则EF＝．9. (2019，山西，3分）如图，在△ABC中，∠BAC=90°，AB=AC=10cm，点D为△ABC内一点，∠BAD=15°，AD=6cm，连接BD，将△ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，连接DE，DE 交AC于点F，则CF的长为 cm.10. （2019•广西北部湾•8分）如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（2，－1）、B（1，－2）、C（3，－3）.（1）将△ABC向上平移4个单位长度得到△A1B1C1，请画出△A1B1C1;（2）请画出△ABC关于y轴对称的△A2B2C2;（3）请写出A1、A2的坐标.11. （2018•宁波）如图，在△ABC中，∠ACB=90°，AC=BC，D是AB边上一点（点D与A，B不重合），连结CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连结DE交BC于点F，连接BE．（1）求证：△ACD≌△BCE；（2）当AD=BF时，求∠BEF的度数．14，点D，E分别在边12. (2019•浙江丽水•12分)如图，在等腰Rt△ABC中，∠ACB＝90°，AB＝2AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF．(1)如图1，若AD＝BD，点E与点C重合，AF与DC相交于点O．求证：BD＝2DO．(2)已知点G为AF的中点．①如图2，若AD＝BD，CE＝2，求DG的长．②若AD＝6BD，是否存在点E，使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由．【参考答案】【典例解析】【例题1】（2019•湖北省随州市•3分）如图，在平面直角坐标系中，Rt△ABC的直角顶点C的坐标为（1，0），点A在x轴正半轴上，且AC=2．将△ABC先绕点C逆时针旋转90°，再向左平移3个单位，则变换后点A的对应点的坐标为______．【答案】（-2，2）【解析】解：∵点C的坐标为（1，0），AC=2，∴点A的坐标为（3，0），如图所示，将Rt△ABC先绕点C逆时针旋转90°，则点A′的坐标为（1，2），再向左平移3个单位长度，则变换后点A′的对应点坐标为（-2，2），故答案为：（-2，2）．根据旋转变换的性质得到旋转变换后点A的对应点坐标，根据平移的性质解答即可．本题考查的是坐标与图形变化旋转和平移，掌握旋转变换、平移变换的性质是解题的关键．【例题2】（2019•浙江绍兴•12分）如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10．（1）在旋转过程中，①当A，D，M三点在同一直线上时，求AM的长．②当A，D，M三点为同一直角三角形的顶点时，求AM的长．（2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2，此时∠AD2C＝135°，CD2＝60，求BD2的长．【分析】（1）①分两种情形分别求解即可．②显然∠MAD不能为直角．当∠AMD为直角时，根据AM2＝AD2﹣DM2，计算即可，当∠ADM＝90°时，根据AM2＝AD2+DM2，计算即可．（2）连接CD．首先利用勾股定理求出CD1，再利用全等三角形的性质证明BD2＝CD1即可．【解答】解：（1）①AM＝AD+DM＝40，或AM＝AD﹣DM＝20．②显然∠MAD不能为直角．当∠AMD为直角时，AM2＝AD2﹣DM2＝302﹣102＝800，∴AM＝202或（﹣202舍弃）．当∠ADM＝90°时，AM2＝AD2+DM2＝302+102＝1000，∴AM＝1010或（﹣1010舍弃）．综上所述，满足条件的AM的值为202或1010．（2）如图2中，连接CD．由题意：∠D1AD2＝90°，AD1＝AD2＝30，∴∠AD2D1＝45°，D1D2＝302，∵∠AD2C＝135°，∴∠CD2D1＝90°，∴CD1＝＝6，∵∠BAC＝∠A1AD2＝90°，∴∠BAC﹣∠CAD2＝∠D2AD1﹣∠CAD2，∴∠BAD1＝∠CAD2，∵AB＝AC，AD2＝AD1，∴△BAD2≌△CAD1（SAS），∴BD2＝CD1＝6．【点评】本题属于四边形综合题，考查了等腰直角三角形的性质，勾股定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．【例题3】（2018•自贡）如图，已知∠AOB=60°，在∠AOB的平分线OM上有一点C，将一个120°角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E．（1）当∠DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；（2）当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；（3）当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．【分析】（1）先判断出∠OCE=60°，再利用特殊角的三角函数得出OD=OC，同OE=OC，即可得出结论；（2）同（1）的方法得OF+OG=OC，再判断出△CFD≌△CGE，得出DF=EG，最后等量代换即可得出结论；（3）同（2）的方法即可得出结论．【解答】解：（1）∵OM是∠AOB的角平分线，∴∠AOC=∠BOC=∠AOB=30°，∵CD⊥OA，∴∠ODC=90°，∴∠OCD=60°，∴∠OCE=∠DCE﹣∠OCD=60°，在Rt△OCD中，OD=OC•cos30°=OC，同理：OE=OC，∴OD+OE=OC；（2）（1）中结论仍然成立，理由：过点C作CF⊥OA于F，CG⊥OB于G，∴∠OFC=∠OGC=90°，∵∠AOB=60°，∴∠FCG=120°，同（1）的方法得，OF=OC，OG=OC，∴OF+OG=OC，∵CF⊥OA，CG⊥OB，且点C是∠AOB的平分线OM上一点，∴CF=CG，∵∠DCE=120°，∠FCG=120°，∴∠DCF=∠ECG，∴△CFD≌△CGE，∴DF=EG，∴OF=OD+DF=OD+EG，OG=OE﹣EG，∴OF+OG=OD+EG+OE﹣EG=OD+OE，∴OD+OE=OC；（3）（1）中结论不成立，结论为：OE﹣OD=OC，理由：过点C作CF⊥OA于F，CG⊥OB于G，∴∠OFC=∠OGC=90°，∵∠AOB=60°，∴∠FCG=120°，同（1）的方法得，OF=OC，OG=OC，∴OF+OG=OC，∵CF⊥OA，CG⊥OB，且点C是∠AOB的平分线OM上一点，∴CF=CG，∵∠DCE=120°，∠FCG=120°，∴∠DCF=∠ECG，∴△CFD≌△CGE，∴DF=EG，∴OF=DF﹣OD=EG﹣OD，OG=OE﹣EG，∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD，∴OE﹣OD=OC．【达标检测】1. （2018海南）（3.00分）如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（）A．6 B．8 C．10 D．12【分析】根据旋转的性质得出AC=AC1，∠BAC1=90°，进而利用勾股定理解答即可．【解答】解：∵将△ABC绕点A逆时针旋转60°得到△AB1C1，∴AC=AC1，∠CAC1=90°，∵AB=8，AC=6，∠BAC=30°，∴∠BAC1=90°，AB=8，AC1=6，∴在Rt△BAC1中，BC1的长=，故选：C．2. （2017山东泰安）如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为（）A．30° B．60° C．90° D．120°【分析】根据题意确定旋转中心后即可确定旋转角的大小．【解答】解：如图：显然，旋转角为90°，故选C．3. （2019•湖北省荆门市•3分）如图，Rt△OCB的斜边在y轴上，OC3，含30°角的顶点与原点重合，直角顶点C在第二象限，将Rt△OCB绕原点顺时针旋转120°后得到△OC′B'，则B点的对应点B′的坐标是（）A．（3，﹣1）B．（1，﹣3）C．（2，0）D．（3，0）【分析】如图，利用含30度的直角三角形三边的关系得到BC＝1，再利用旋转的性质得到OC′＝OC ＝3，B′C′＝BC＝1，∠B′C′O＝∠BCO＝90°，然后利用第四象限点的坐标特征写出点B′的坐标．【解答】解：如图，在Rt△OCB中，∵∠BOC＝30°，∴BC＝33OC＝33×3＝1，∵Rt△OCB绕原点顺时针旋转120°后得到△OC′B'，∴OC′＝OC＝3，B′C′＝BC＝1，∠B′C′O＝∠BCO＝90°，∴点B′的坐标为（3，﹣1）．故选：A．【点评】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．4. 如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF 中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（）A．5 B．4 C．D．【分析】由△DQF∽△FQE，推出===，由此求出EQ、FQ即可解决问题．【解答】解：如图，在等腰直角三角形△DEF中，∠EDF=90°，DE=DF，∠1=∠2=∠3，∵∠1+∠QEF=∠3+∠DFQ=45°，∴∠QEF=∠DFQ，∵∠2=∠3，∴△DQF∽△FQE，∴===，∵DQ=1，∴FQ=，EQ=2，∴EQ+FQ=2+，故选D【点评】1．应用旋转解决几何问题时：(1)抓住旋转中的“变”与“不变”；(2)找准旋转前后的对应点和对应线段、旋转角等；(3)充分利用旋转过程中线段、角之间的关系．2．当旋转方向没有确定时，需要分类，即分逆时针和顺时针两种情况讨论．5. （2019浙江丽水3分）将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则的值是（）A．522- B ．2﹣1 C ． D ．22【分析】连接HF ，设直线MH 与AD 边的交点为P ，根据剪纸的过程以及折叠的性质得PH ＝MF 且正方形EFGH 的面积＝×正方形ABCD 的面积，从而用a 分别表示出线段GF 和线段MF 的长即可求解．【解答】解：连接HF ，设直线MH 与AD 边的交点为P ，如图：由折叠可知点P 、H 、F 、M 四点共线，且PH ＝MF ，设正方形ABCD 的边长为2a ，则正方形ABCD 的面积为4a 2，∵若正方形EFGH 与五边形MCNGF 的面积相等∴由折叠可知正方形EFGH 的面积＝15×正方形ABCD 的面积＝245a ， ∴正方形EFGH 的边长GF ＝245a ＝255a ∴HF＝2GF ＝2105a ∴MF＝PH ＝210252a a -＝5105a - ∴510-2552- 故选：A ．【点评】本题主要考查了剪纸问题、正方形的性质以及折叠的性质，由剪纸的过程得到图形中边的关系是解题关键．6. (2019•湖南常德•3分)如图，已知△ABC 是等腰三角形，AB ＝AC ，∠BAC＝45°，点D 在AC 边上，将△ABD 绕点A 逆时针旋转45°得到△ACD′，且点D′、D 、B 三点在同一条直线上，则∠ABD 的度数是 ．【考点】旋转．【分析】由旋转的性质可得∠BAC＝∠CAD'＝45°，AD＝AD'，由等腰三角形的性质可得∠AD'D＝67.5°，∠D'AB＝90°，即可求∠ABD的度数．【解答】解：∵将△ABD绕点A逆时针旋转45°得到△ACD′，∴∠BAC＝∠CAD'＝45°，AD＝AD'，∴∠AD'D＝67.5°，∠D'AB＝90°，∴∠ABD＝22.5°．故答案为22.5°．【点评】本题考查了旋转的性质，等腰三角形的性质，熟练运用旋转的性质是本题的关键．7. (2019•湖南益阳•4分)在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，使各顶点仍在格点上，则其旋转角的度数是．【考点】旋转．【分析】根据旋转角的概念找到∠BOB′是旋转角，从图形中可求出其度数．【解答】解：根据旋转角的概念：对应点与旋转中心连线的夹角，可知∠BOB′是旋转角，且∠BOB′＝90°，故答案为90°．【点评】本题主要考查了旋转角的概念，解题的关键是根据旋转角的概念找到旋转角．8. （2019•海南省•4分）如图，将Rt△ABC的斜边AB绕点A顺时针旋转α（0°＜α＜90°）得到AE，直角边AC绕点A逆时针旋转β（0°＜β＜90°）得到AF，连结EF．若AB＝3，AC＝2，且α+β＝∠B，则EF＝．【分析】由旋转的性质可得AE ＝AB ＝3，AC ＝AF ＝2，由勾股定理可求EF 的长．【解答】解：由旋转的性质可得AE ＝AB ＝3，AC ＝AF ＝2，∵∠B+∠BAC ＝90°，且α+β＝∠B ，∴∠BAC+α+β＝90°∴∠EAF ＝90°∴EF ＝＝ 故答案为： 【点评】本题考查了旋转的性质，勾股定理，灵活运用旋转的性质是本题的关键．9. (2019，山西，3分）如图，在△ABC 中，∠BAC=90°，AB=AC=10cm ，点D 为△ABC 内一点，∠BAD=15°，AD=6cm ，连接BD ，将△ABD 绕点A 逆时针方向旋转，使AB 与AC 重合，点D 的对应点E ，连接DE ，DE 交AC 于点F ，则CF 的长为 cm.【解析】过点A 作AG⊥DE 于点G ，由旋转可知：AD=AE ，∠DAE=90°，∠CAE=∠BAD=15° ∴∠AED=45°；在△AEF 中：∠AFD=∠AED+∠CAE=60°在Rt△ADG 中：AG=DG=232=AD 在Rt△AF G 中：622,63====FG AF AG GF ∴6210-=-=AF AC CF故答案为：6210-10. （2019•广西北部湾•8分）如图，在平面直角坐标系中，已知△ABC 的三个顶点坐标分别是A （2，－1）、B （1，－2）、C （3，－3）.（1）将△ABC 向上平移4个单位长度得到△A 1B 1C 1，请画出△A 1B 1C 1;（2）请画出△ABC关于y轴对称的△A2B2C2;（3）请写出A1、A2的坐标.【答案】解：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求；（3）A1（2，3），A2（-2，-1）．【解析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）直接利用轴对称的性质得出对应点位置进而得出答案；（3）利用所画图象得出对应点坐标．此题主要考查了轴对称变换以及平移变换，正确得出对应点位置是解题关键．11. （2018•宁波）如图，在△ABC中，∠ACB=90°，AC=BC，D是AB边上一点（点D与A，B不重合），连结CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连结DE交BC于点F，连接BE．（1）求证：△ACD≌△BCE；（2）当AD=BF时，求∠BEF的度数．【分析】（1）由题意可知：CD=CE，∠DCE=90°，由于∠ACB=90°，所以∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，所以∠ACD=∠BCE，从而可证明△ACD≌△BCE（SAS）（2）由△ACD≌△BCE（SAS）可知：∠A=∠CBE=45°，BE=BF，从而可求出∠BEF的度数．【解答】解：（1）由题意可知：CD=CE，∠DCE=90°，∵∠ACB=90°，∴∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，∴∠ACD=∠BCE，在△ACD与△BCE中，∴△ACD≌△BCE（SAS）（2）∵∠ACB=90°，AC=BC，∴∠A=45°，由（1）可知：∠A=∠CBE=45°，∵AD=BF，∴BE=BF，∴∠BEF=67.5°【点评】图形在旋转过程中，图中的每一个点与旋转中心的连线都绕着旋转中心转动了相同的角度，对应线段相等，对应角相等．在利用此性质解决问题时，应充分寻找对应线段、对应角．14，点D，E分别在边12. (2019•浙江丽水•12分)如图，在等腰Rt△ABC中，∠ACB＝90°，AB＝2AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF．(1)如图1，若AD＝BD，点E与点C重合，AF与DC相交于点O．求证：BD＝2DO．(2)已知点G为AF的中点．①如图2，若AD＝BD，CE＝2，求DG的长．②若AD＝6BD，是否存在点E，使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由．【考点】三角形综合．【分析】(1)如图1中，首先证明CD＝BD＝AD，再证明四边形ADFC是平行四边形即可解决问题．(2)①作DT⊥BC于点T，FH⊥BC于H．证明DG是△ABF的中位线，想办法求出BF即可解决问题．②分三种情形情形：如图3﹣1中，当∠DEG＝90°时，F，E，G，A共线，作DT⊥BC于点T，FH⊥BC 于H．设EC＝x．构建方程解决问题即可．如图3﹣2中，当∠EDG＝90°时，取AB的中点O，连接OG．作EH⊥AB于H．构建方程解决问题即可．如图3﹣3中，当∠DGE＝90°时，构造相似三角形，利用相似三角形的性质构建方程解决问题即可．【解答】(1)证明：如图1，∵CA＝CB，∠ACB＝90°，BD＝AD，∴CD⊥AB，CD＝AD＝BD，∵CD＝CF，∴AD＝CF，∵∠ADC＝∠DCF＝90°，∴AD∥CF，∴四边形ADFC是平行四边形，∴OD＝OC，∴BD＝2OD．(2)①解：如图2，作DT⊥BC于点T，FH⊥BC于H．由题意：BD＝AD＝CD＝2，BC2BD＝14，∵DT⊥BC，∴BT＝TC＝7，∵EC＝2，∴TE＝5，∵∠DTE＝∠EHF＝∠DEF＝90°，∴∠DET+∠TDE＝90°，∠DET+∠FEH＝90°，∴∠TDE＝∠FEH，∵ED＝EF ，∴△DTE≌△EHF(AAS)，∴FH＝ET ＝5，∵∠DDBE＝∠DFE＝45°，∴B，D ，E ，F 四点共圆，∴∠DBF+∠DEF＝90°，∴∠DBF＝90°，∵∠DBE＝45°，∴∠FBH＝45°，∵∠BHF＝90°，∴∠HBF＝∠HFB＝45°，∴BH＝FH ＝5，∴BF＝52， ∵∠ADC＝∠ABF＝90°，∴DG∥BF， ∵AD＝DB ，∴AG＝GF ，∴DG＝12BF ＝522． ②解：如图3﹣1中，当∠DEG＝90°时，F ，E ，G ，A 共线，作DT⊥BC 于点T ，FH⊥BC 于H ．设EC ＝x ．∵AD＝6BD ，∴BD＝AB ＝22，∵DT⊥BC，∠DBT＝45°，∴DT＝BT ＝2，∵△DTE≌△EHF，∴EH＝DT ＝2，∴BH＝FH ＝12－x ，∵FH∥AC，∴＝，∴14122x x -=， 整理得：x 2－12x+28＝0，解得x 2． 如图3﹣2中，当∠EDG＝90°时，取AB 的中点O ，连接OG ．作EH⊥AB 于H ．设EC ＝x ，由2①可知BF 2 (12－x)，OG ＝12BF 2 (12－x)，∵∠EHD＝∠EDG＝∠DOG＝90°，∴∠ODG+∠OGD＝90°，∠ODG+∠EDH＝90°，∴∠DGO＝∠HDE，∴△EHD∽△DOG，∴＝，∴＝，整理得：x2－36x+268＝0，解得x＝18－2或18+2(舍弃)，如图3﹣3中，当∠DGE＝90°时，取AB的中点O，连接OG，CG，作DT⊥BC于T，FH⊥BC于H，EK⊥CG 于K．设EC＝x．∵∠DBE＝∠DFE＝45°，∴D，B，F，E四点共圆，∴∠DBF+∠DEF＝90°，∵∠DEF＝90°，∴∠DBF＝90°，∵AO＝OB，AG＝GF，∴OG∥BF，∴∠AOG＝∠ABF＝90°，∴OG⊥AB，∵OG垂直平分线段AB，∵CA＝CB，∴O，G，C共线，由△DTE≌△EHF，可得EH＝DT＝BT＝2，ET＝FH＝12－x，BF＝2 (12－x)，OG＝BF＝22(12－x)，CK＝EK＝22x，GK＝72－22(12－x)－22x，由△OGD∽△KEG，可得＝，∴＝，解得x＝2．综上所述，满足条件的EC的值为2或18－142．【点评】本题属于几何变换综合题，考查了等腰直角三角形的性质，平行四边形的判定和性质，全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形或相似三角形解决问题，属于中考压轴题．。

BE DF 1
A
D
2
2
⑤CE= 2 DM,DF= BG,EF= GM, ⑥ = =
CE FC 2
M
⑦△AEF的边EF上的高等于正方形的边长；
⑧△EFC的周长等于正方形的边长的2倍.
F
角度之间的关系： ①∠AEB=∠AEF,∠AFE=∠AFD
G
O
②根据下面共圆,每个共圆都至少可以得到四队相等的角.
四点共圆：①ABEM ②ADFG ③GEFM ④CEMF ⑤CEGMF

=


=


= .
A
(1)∵∠MEN=∠MFN=45º,∴M、N、F、E四点共圆
D
45º
∴∠ANM=∠AEF,∠AMN=∠AFE,
∴△AMN∽△AFE.
N
F
M
B
E
C
变式训练
考点3-1
半角模型---90°+45°
【变式6】如图,E,F是正方形ABCD的两边上的点,∠EAF=45º,BD交AE,AF于
A
上且∠EDF=60º.求证：EF=BE+CF.
【分析】将△BDN绕点D顺时针旋转120º得△DCG,
E
F
易证：△DBE≌△DCG(SAS)→DE=DG,∠FDG=∠FDE=60º
易证：△DFE≌△DFG(SAS)→EF=GF,
∴EF=GF=GC+CF=BE+CF.
B
60º
D
C
针对训练
考点3-2
半角模型---120°+60°
图形示例
A
模型分析
当一个角包含着这个角的半角
等边三角形
,常将半角两边的三角形通过

M D N E C BF A 初三专题练习——旋转问题 姓名______________ 学号_____________一、手拉手模型（特点——公共点是等腰三角形的顶点）如图，易证：'ABB ∆≌'ACC ∆这就是传说中的“旋转一施二”，又称为“手拉手模型”1、已知：如图，点C 为线段AB 上一点，ACM ∆、CBN ∆是等边三角形．求证：∠AFM=60°2、如图，在等腰ABC Rt ∆中，BC BA =，︒=∠90ABC ，点D 在AC 上，将ABD ∆绕点B 顺时针方向旋转︒90后，得到CBE ∆（1）求DCE ∠的度数；（2）若4=AB ，AD CD 3=，求DE 的长。

3、等边ABC ∆中，4=AD ，3=DC ，5=BD ，求ADC ∠的度数。

A B C D4、如图，在凸四边形ABCD 中，30BCD ∠=︒,60DAB AD AB ∠=︒=，．求证：222AC CD BC =+5、已知ABC ∆，以AC 为边在ABC ∆外作等腰ACD ∆，其中AC AD =。

⑴如图①，若2DAC ABC ∠=∠，AC BC =，四边形ABCD 是平行四边形，则_____ABC ∠= ⑵如图②，若30ABC ∠=︒，ACD ∆是等边三角形，3AB =，4BC =，求BD 的长；6、已知在ABC ∆中，AC AB =，D 是BC 边上一点，连接AD ，在直线AD 右侧作等腰ADE ∆，AE AD =（1）如图1，︒=∠=∠90DAE BAC ，连接CE ，求证：ABD ∆≌ACE ∆（2）如图2，︒=∠=∠120DAE BAC ，2==AC AB ，取AC 边的中点F ，连接EF ，当点D 从B 点运动到C 点过程中，求线段EF 长度的最小值。

（3）如图3，四边形ABCD 中，︒=∠=∠90BCD BAD ，AD AB =，1=DC ，连接AC ，已知2230+=AC ，求AB 的长。

专题18 旋转模型之费马点型1．若一个三角形的最大内角小于120°，则在其内部有一点所对三角形三边的张角均为120°，此时该点叫做这个三角形的费马点．如图1，当△ABC 三个内角均小于120°时，费马点P 在△ABC 内部，此时120APB BPC CPA ∠=∠=∠=︒，PA PB PC ++的值最小．(1)如图2，等边三角形ABC 内有一点P ，若点P 到顶点A ，B ，C 的距离分别为3，4，5，求APB ∠的度数．为了解决本题，小林利用“转化”思想，将△ABP 绕顶点A 旋转到ACP '△处，连接PP '，此时ACP ABP '≌，这样就可以通过旋转变换，将三条线段P A ，PB ，PC 转化到一个三角形中，从而求出APB ∠=______．(2)如图3，在图1的基础上延长BP ，在射线BP 上取点D ，E ，连接AE ，AD ．使AD AP =，DAE PAC ∠=∠，求证：BE PA PB PC =++．(3)如图4，在直角三角形ABC 中 ，90ABC ∠=︒，30ACB ∠=︒，1AB =，点P 为直角三角形ABC 的费马点，连接AP ，BP ，CP ，请直接写出PA PB PC ++的值． 【答案】(1)150°(2)见解析(3)7【分析】（1）由全等三角形的性质得到AP ′＝AP ＝3、CP ′＝BP ＝4，∠AP ′C ＝∠APB ，再根据旋转性质，证明△APP ′为等边三角形，△PP ′C 为直角三角形，最后由∠APB ＝∠AP ′C ＝∠AP ′P ＋∠PP ′C 解答；（2）由费马点的性质得到120APB ∠=︒，60APD ∠=︒，再证明APC ADE ≌ (ASA)，由全等三角形对应边相等的性质解得PC DE =，最后根据线段的和差解答；（3）将△APB 绕点B 顺时针旋转60°至△A ′P ′B 处，连接PP ′，由勾股定理解得3BC =，由旋转的性质，可证明△BPP ′是等边三角形，再证明C 、P 、A ′、P ′四点共线，最后由勾股定理解答． （1）解：∵ACP ABP '≌，∴AP ′＝AP ＝3、CP ′＝BP ＝4，∠AP ′C ＝∠APB ，由题意知旋转角∠P AP ′＝60°，∴△APP ′为等边三角形，PP ′＝AP ＝3，∠AP ′P ＝60°，由旋转的性质可得：AP ′＝AP ＝PP ′=3，CP ′＝4，PC=5，∵32+42=52∴△PP ′C 为直角三角形，且∠PP ′C ＝90°，∴∠APB ＝∠AP ′C ＝∠AP ′P ＋∠PP ′C ＝60°＋90°＝150°；故答案为：150°；（2）证明：∵点P 为△ABC 的费马点，∴120APB ∠=︒，∴60APD ∠=︒，又∵AD AP =，∴APD 为等边三角形∴AP PD AD ==，60PAD ADP ∠=∠=︒，∴120ADE ∠=︒，∴ADE APC ∠=∠，在△APC 和△ADE 中，PAC DAE AP ADAPC ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴APC ADE ≌ (ASA)；∴PC DE =，∵BE BP PD DE =++，∴BE ＝P A ＋PB ＋PC ；（3）解：如图，将△APB 绕点B 顺时针旋转60°至△A ′P ′B 处，连接PP ′，∵在Rt △ABC 中，∠C ＝90°，AC ＝1，∠ABC ＝30°，∴AB ＝2，∴223BC AB AC =-=，把△APB 绕点B 顺时针方向旋转60°得到△A ′P ′B ，∴∠A ′BC ＝∠ABC ＋60°＝30°＋60°＝90°，∵∠C ＝90°，AC ＝1，∠ABC ＝30°，∴AB ＝2AC ＝2，∵△APB 绕点B 顺时针方向旋转60°，得到△A ′P ′B ，∴A ′B ＝AB ＝2，BP ＝BP ′，A ′P ′＝AP ，∴△BPP ′是等边三角形，∴BP ＝PP ′，∠BPP ′＝∠BP ′P ＝60°，∵∠APC ＝∠CPB ＝∠BP A ＝120°，∴∠CPB ＋∠BPP ′＝∠BP ′A ′＋∠BP ′P ＝120°＋60°＝180°，∴C 、P 、A ′、P ′四点共线，在Rt △A ′BC 中，2222(3)27A C A B BC ''=+=+=，∴P A ＋PB ＋PC ＝A ′P ′＋PP ′＋PC ＝A ′C ＝7．【点睛】本题考查全等三角形的判定与性质、等边三角形的判定与性质、勾股定理、旋转的性质、费马点等知识，是重要考点，有难度，掌握相关知识，正确做出辅助线是解题关键．2．如图，四边形ABCD是菱形，AB=4，且∠ABC=∠ABE=60°，G为对角线BD（不含B点）上任意一点，将△ABG绕点B逆时针旋转60°得到△EBF，当AG+BG+CG取最小值时EF的长（）A．33B．23C．33D．43【答案】D【分析】根据“两点之间线段最短”，当G点位于BD与CE的交点处时，AG+BG+CG的值最小，即等于EC的长．【详解】解：如图，∵将△ABG绕点B逆时针旋转60°得到△EBF，∴BE=AB=BC，BF=BG，EF=AG，∴△BFG是等边三角形．∴BF=BG=FG，．∴AG+BG+CG=FE+GF+CG．根据“两点之间线段最短”，∴当G点位于BD与CE的交点处时，AG+BG+CG的值最小，即等于EC的长，过E点作EF⊥BC交CB的延长线于F，∴∠EBF=180°-120°=60°，∵BC=4，∴BF=2，EF=23，在Rt△EFC中，∵EF2+FC2=EC2，∴EC=43．∵∠CBE=120°，∴∠BEF=30°，∵∠EBF=∠ABG=30°，∴EF=BF=FG，∴EF=13CE=433，故选：D．【点睛】本题考查了旋转的性质，菱形的性质，等边三角形的性质，轴对称最短路线问题，正确的作出辅助线是解题的关键．3．如图，已知矩形ABCD，AB＝4，BC＝6，点M为矩形内一点，点E为BC边上任意一点，则MA＋MD＋ME的最小值为______．【答案】4+33【详解】【分析】依然构造60°旋转，将三条折线段转化为一条直线段．分别以AD、AM为边构造等边△ADF、等边△AMG，连接FG，易证△AMD≌△AGF，∴MD＝GF∴ME＋MA＋MD＝ME＋EG＋GF过F作FH⊥BC交BC于H点，线段FH的长即为所求的最小值．4．问题背景：如图，将ABC ∆绕点A 逆时针旋转60°得到ADE ∆，DE 与BC 交于点P ，可推出结论：PA PC PE +=问题解决：如图，在MNG ∆中，6MN =，75M ∠=︒，42MG =O 是MNG ∆内一点，则点O 到MNG ∆三个顶点的距离和的最小值是___________【答案】229【分析】如图，将△MOG 绕点M 逆时针旋转60°，得到△MPQ ，易知△MOP 为等边三角形，继而得到点O 到三顶点的距离为：ON ＋OM ＋OG ＝ON ＋OP ＋PQ ，由此可以发现当点N 、O 、P 、Q 在同一条直线上时，有ON ＋OM ＋OG 最小，此时，∠NMQ ＝75°+60°＝135°，过Q 作QA ⊥NM 交NM 的延长线于A ，利用勾股定理进行求解即可得.【详解】如图，将△MOG 绕点M 逆时针旋转60°，得到△MPQ ，显然△MOP 为等边三角形，∴，OM ＋OG ＝OP ＋PQ ，∴点O 到三顶点的距离为：ON ＋OM ＋OG ＝ON ＋OP ＋PQ ，∴当点N 、O 、P 、Q 在同一条直线上时，有ON ＋OM ＋OG 最小，此时，∠NMQ ＝75°+60°＝135°，过Q 作QA ⊥NM 交NM 的延长线于A ，则∠MAQ=90°，∴∠AMQ ＝180°-∠NMQ=45°，∵MQ＝MG＝42，∴AQ＝AM＝MQ•cos45°=4，∴NQ＝2222AN AQ+=++=，(46)4229故答案为229.【点睛】本题考查了旋转的性质，最短路径问题，勾股定理，解直角三角形等知识，综合性较强，有一定的难度，正确添加辅助线是解题的关键.5．如图，△ABC中，∠BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为2BC＝_____．【答案】62-【分析】如图将△ABP绕点A顺时针旋转60°得到△AMG．连接PG，CM．首先证明当M，G，P，C共线时，PA+PB+PC的值最小，最小值为线段CM的长，想办法求出AC的长即可解决问题.【详解】如图将△ABP绕点A顺时针旋转60°得到△AMG．连接PG，CM．∵AB=AC，AH⊥BC，∴∠BAP=∠CAP，∵PA=PA，∴△BAP≌△CAP（SAS），∴PC=PB，∵MG=PB，AG=AP，∠GAP=60°，∴△GAP是等边三角形，∴PA=PG，∴PA+PB+PC=CP+PG+GM，∴当M，G，P，C共线时，PA+PB+PC的值最小，最小值为线段CM的长，∵AP+BP+CP的最小值为22，∴CM=22，∵∠BAM=60°，∠BAC=30°，∴∠MAC=90°，∴AM=AC=2，AB=1，AN=3，CN=2-3，作BN⊥AC于N．则BN=12∴BC=2222++--．BN CN=1(23)=62故答案为62-．【点睛】本题考查轴对称-最短问题，等腰三角形的性质，等边三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用两点之间线段最短解决问题6．如图，四边形ABCD是菱形，A B=6，且∠ABC=60° ，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为________．【答案】63【分析】以BM为边作等边△BMN，以BC为边作等边△BCE，如图，则△BCM≌△BEN，由全等三角形的对应边相等得到CM=NE，进而得到AM+MB+CM=AM+MN+NE．当A、M、N、E四点共线时取最小值AE．根据等腰三角形“三线合一”的性质得到BH⊥AE，AH=EH，根据30°直角三角形三边的关系即可得出结论．【详解】以BM为边作等边△BMN，以BC为边作等边△BCE，则BM=BN=MN，BC=BE=CE，∠MBN=∠CBE=60°，∴∠MBC=∠NBE，∴△BCM≌△BEN，∴CM=NE，∴AM+MB+CM=AM+MN+NE．当A 、M 、N 、E 四点共线时取最小值AE ．∵AB =BC =BE =6，∠ABH =∠EBH =60°，∴BH ⊥AE ，AH =EH ，∠BAH =30°，∴BH =12AB =3，AH =3BH =33，∴AE =2AH =63． 故答案为63．【点睛】本题考查了菱形的性质，全等三角形的判定与性质，等边三角形的性质．难度比较大．作出恰当的辅助线是解答本题的关键．7．【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马，提出一个问题：求作三角形内的一个点，使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”． 如图，点P 是ABC 内的一点，将APC △绕点A 逆时针旋转60°到AP C ''，则可以构造出等边APP '，得AP PP '=，CP CP '=，所以PA PB PC ++的值转化为PP PB P C +'+''的值，当B ，P ，P '，C 四点共线时，线段BC 的长为所求的最小值，即点P 为ABC 的“费马点”．(1)【拓展应用】如图1，点P 是等边ABC 内的一点，连接PA ，PB ，PC ，将PAC △绕点A 逆时针旋转60°得到AP C ''．①若3PA =，则点P 与点P '之间的距离是______；②当3PA =，5PB =，4PC =时，求AP C ∠'的大小；(2)如图2，点P 是ABC 内的一点，且90BAC ∠=︒，6AB =，23AC =PA PB PC ++的最小值．【答案】(1)①3；②150°； (2)221【分析】（1）①根据旋转的性质即可求出PP '的值；②先证△ABP ≌ACP '△，利用全等的性子求出对应的边长，通过勾股定理的逆定理得到90CPP ∠=︒′，即可求出AP C ∠'的大小；（2）将△APC 绕C 点顺时针旋转60°得到A P C ′′，先求出120BCA ∠=︒′，然后证明CPP △′为等边三角形，当B 、P 、P '、A '四点共线时，PA PB PC ++和最小，用勾股定理求出BA '的值即可．(1)①如图，将PAC △绕A 逆时针旋转60°，则AP AP ='，60PAP ∠'=︒，∴APP '为等边三角形，3 PP PA∴==′；②∵△ABC为等边三角形，∴AB=AC，∠BAP+∠P AC=60°，又∵APP'是等边三角形，∴∠P AC+CAP∠′=60°，∴∠BAP=CAP∠′，在△ABP与ACP'△中，AB ACBAP CAPAP AP=⎧⎪∠=∠⎨⎪=⎩′′，∴△ABP≌ACP'△（SAS），∴5,3,4,BP CP PP PC====′′∴222PP PC CP+=′′，90CPP∴∠=︒′，60+90=150APC APP CPP∴∠=∠+∠︒︒︒′′=，又∵旋转，∴=150AP C APC∠=∠=︒′；(2)如图，将△APC绕C点顺时针旋转60°得到A P C′′，则,60ACP A CP ACP ACP∠=∠∠+∠=︒′′′，在Rt ABC中，()222262343BC AB AC=+=+=，1,30,602AC BC ABC ACB=∴∠=︒∠=︒，60ACP BCP ∴∠+∠=︒，又∵,60ACP A CP ACP ACP ∠=∠∠+∠=︒′′′， 60ACP ACP ∴∠+∠=︒′′′，120BCP ACP ACP ACP∴+∠+∠+∠=︒′′′， 过A '作A D '⊥BC 交BC 的延长线于点D ，则18012060ACD BCD BCA ∠=∠-∠=︒-︒=︒′′，30CA D ∴∠=︒′，23,A C AC ==′3CD ∴=（30°所对的直角边等于斜边的一半），223A D AC CD ∴=-=′′，60,PCP PC CP ∠=︒=′′，CPP ∴'为等边三角形，当B 、P 、P '、A '四点共线时，PA PB PC ++和最小， 在Rt BDA △′中，43353,3BD BC CD DA =+=+==′， ()2222533221BA BD DA ∴=+=+=′′，∴PA PB PC ++的最小值为221．【点睛】本题考查了旋转变换，全等三角形的判定和性质，解题的关键在于能够添加辅助线构造全等三角形解决问题．8．背景资料：在已知ABC 所在平面上求一点P ，使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图1，当ABC 三个内角均小于120°时，费马点P 在ABC 内部，当120APB APC CPB ∠=∠=∠=︒时，则PA PB PC ++取得最小值．(1)如图2，等边ABC 内有一点P ，若点P 到顶点A 、B 、C 的距离分别为3，4，5，求APB ∠的度数，为了解决本题，我们可以将ABP △绕顶点A 旋转到ACP '△处，此时ACP ABP '≌这样就可以利用旋转变换，将三条线段PA 、PB 、PC 转化到一个三角形中，从而求出APB ∠=_______； 知识生成：怎样找三个内角均小于120°的三角形的费马点呢？为此我们只要以三角形一边在外侧作等边三角形并连接等边三角形的顶点与ABC 的另一顶点，则连线通过三角形内部的费马点．请同学们探索以下问题．(2)如图3，ABC 三个内角均小于120°，在ABC 外侧作等边三角形ABB '，连接CB '，求证：CB '过ABC 的费马点．(3)如图4，在RT ABC 中，90C ∠=︒，1AC =，30ABC ∠=︒，点P 为ABC 的费马点，连接AP 、BP 、CP ，求PA PB PC ++的值．(4)如图5，在正方形ABCD 中，点E 为内部任意一点，连接AE 、BE 、CE ，且边长2AB =；求AE BE CE ++的最小值．【答案】(1)150°； (2)见详解； (3)7； (4)62+．【分析】（1）根据旋转性质得出ABP △≌ACP '△，得出∠BAP =∠CAP′，∠APB =∠AP′C ，AP =AP′=3，BP=CP′=4，根据△ABC 为等边三角形，得出∠BAC =60°，可证△APP′为等边三角形，PP′=AP =3，∠AP′P =60°，根据勾股定理逆定理222223425PP P C PC ''+=+==，得出△PP′C 是直角三角形，∠PP′C =90°，可求∠AP′C =∠APP +∠PPC =60°+90°=150°即可；（2）将△APB 逆时针旋转60°，得到△AB′P′，连结PP′，根据△APB ≌△AB′P′，AP =AP′，PB =PB′，AB =AB′，根据∠P AP′=∠BAB′=60°，△APP′和△ABB′均为等边三角形，得出PP′=AP ，根据PA PB PC PP P B PC '''++=++，根据两点之间线段最短得出点C ，点P ，点P′，点B′四点共线时，PA PB PC ++最小=CB′，点P 在CB′上即可；（3）将△APB 逆时针旋转60°，得到△AP′B′，连结BB′，PP′，得出△APB ≌△AP′B′，可证△APP′和△ABB′均为等边三角形，得出PP′=AP ，BB′=AB ，∠ABB′=60°，根据PA PB PC PP P B PC '''++=++，可得点C ，点P ，点P′，点B′四点共线时，PA PB PC ++最小=CB′，利用30°直角三角形性质得出AB =2AC =2，根据勾股定理BC =2222213AB AC -=-=，可求BB′=AB =2，根据∠CBB′=∠ABC +∠ABB′=30°+60°=90°，在Rt △CBB′中，B′C =()2222327BC BB '+=+=即可；（4）将△BCE 逆时针旋转60°得到△CE′B′，连结EE′，BB′，过点B′作B′F ⊥AB ，交AB 延长线于F ，得出△BCE ≌△CE′B′，BE =B′E′，CE =CE ′，CB =CB′，可证△ECE′与△BCB′均为等边三角形，得出EE ′=EC ，BB′=BC ，∠B′BC =60°，AE BE CE AE EE E B '''++=++，得出点C ，点E ，点E′，点B′四点共线时，AE BE CE AE EE E B '''++=++最小=AB′，根据四边形ABCD 为正方形，得出AB =BC =2，∠ABC =90°，可求∠FBB′=180°-∠ABC -∠CBB′=180°-90°-60°=30°，根据30°直角三角形性质得出BF =112122BB '=⨯=，勾股定理BF =2222213BB B F ''-=-=，可求AF =AB +BF =2+3，再根据勾股定理AB′=()222223162AF B F '+=++=+即可．(1)解：连结PP′， ∵ABP △≌ACP '△，∴∠BAP =∠CAP′，∠APB =∠AP′C ，AP =AP′=3，BP=CP′=4， ∵△ABC 为等边三角形， ∴∠BAC =60°∴∠P AP ′=∠P AC +∠CAP ′=∠P AC +∠BAP =60°， ∴△APP′为等边三角形， ,∴PP′=AP =3，∠AP′P =60°， 在△P′PC 中，PC =5，222223425PP P C PC ''+=+==， ∴△PP′C 是直角三角形，∠PP′C =90°， ∴∠AP′C =∠APP +∠PPC =60°+90°=150°， ∴∠APB =∠AP′C =150°， 故答案为150°；(2)证明：将△APB 逆时针旋转60°，得到△AB′P′，连结PP′， ∵△APB ≌△AB′P′，∴AP =AP′，PB =PB′，AB =AB′， ∵∠P AP′=∠BAB′=60°，∴△APP′和△ABB′均为等边三角形， ∴PP′=AP ，∵PA PB PC PP P B PC '''++=++，∴点C ，点P ，点P′，点B′四点共线时，PA PB PC ++最小=CB′， ∴点P 在CB′上， ∴CB '过ABC 的费马点．(3)解：将△APB 逆时针旋转60°，得到△AP′B′，连结BB′，PP′， ∴△APB ≌△AP′B′， ∴AP′=AP ，AB′=AB ， ∵∠P AP′=∠BAB′=60°，∴△APP′和△ABB′均为等边三角形， ∴PP′=AP ，BB′=AB ，∠ABB′=60°， ∵PA PB PC PP P B PC '''++=++∴点C ，点P ，点P′，点B′四点共线时，PA PB PC ++最小=CB′，∵90C ∠=︒，1AC =，30ABC ∠=︒，∴AB =2AC =2，根据勾股定理BC =2222213AB AC -=-= ∴BB′=AB =2，∵∠CBB′=∠ABC +∠ABB′=30°+60°=90°， ∴在Rt △CBB′中，B′C =()2222327BC BB '+=+=∴PA PB PC ++最小=CB′=7；(4)解：将△BCE 逆时针旋转60°得到△CE′B′，连结EE′，BB′，过点B′作B′F ⊥AB ，交AB 延长线于F ， ∴△BCE ≌△CE′B′，∴BE =B′E′，CE =CE ′，CB =CB′， ∵∠ECE′=∠BCB′=60°，∴△ECE′与△BCB′均为等边三角形， ∴EE ′=EC ，BB′=BC ，∠B′BC =60°， ∵AE BE CE AE EE E B '''++=++，∴点C ，点E ，点E′，点B′四点共线时，AE BE CE AE EE E B '''++=++最小=AB′， ∵四边形ABCD 为正方形， ∴AB =BC =2，∠ABC =90°，∴∠FBB′=180°-∠ABC -∠CBB′=180°-90°-60°=30°， ∵B′F ⊥AF ，∴BF =112122BB '=⨯=，BF =2222213BB B F ''-=-=，∴AF =AB +BF =2+3， ∴AB′=()222223162AF B F '+=++=+，∴AE BE CE ++最小=AB′=62+．【点睛】本题考查图形旋转性质，等边三角形判定与性质，勾股定理，直角三角形判定与性质，两点之间线段最短，四点共线，正方形性质，30°直角三角形性质，掌握图形旋转性质，等边三角形判定与性质，勾股定理，直角三角形判定与性质，两点之间线段最短，四点共线，正方形性质，30°直角三角形性质是解题关键．9．如图，在△ABC 中，∠BAC ＝90°，AB ＝AC ＝1，P 是△ABC 内一点，求P A ＋PB ＋PC 的最小值．【答案】22+62【分析】以点A 为旋转中心，将△ABP 顺时针旋转60°得到△AMN ，连接BN ．根据△PAM 、△ABN 都是等边三角形，可得PA+PB+PC=CP+PM+MN ；根据当C 、P 、M 、N 四点共线时，由CA=CB ，NA=NB 可得CN 垂直平分AB ，进而求得PA+PB+PC 的最小值．【详解】证明：如图所示，以点A 为旋转中心，将△ABP 顺时针旋转60°得到△AMN ，连接BN ．由旋转可得，△AMN ≌△ABP ，∴MN=BP ，PA=AM ，∠PAM=60°=∠BAN ，AB=AN ， ∴△PAM 、△ABN 都是等边三角形， ∴PA=PM ，∴PA+PB+PC=PM+MN+PC ； （3）当AC=BC=1时，AB=22，当C 、P 、M 、N 四点共线时，由CA=CB ，NA=NB 可得CN 垂直平分AB ， ∴AQ=12AB=22=CQ ，NQ=62， 此时CN=CP+PM+MN=PA+PB+PC=22+6210．【问题提出】（1）如图1，四边形ABCD 是正方形，ABE △是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60︒得到BN ，连接EN 、AM ，CM ．若连接MN ，则BMN △的形状是________．（2）如图2，在Rt ABC 中，90BAC ∠=︒，10AB AC +=，求BC 的最小值． 【问题解决】（3）如图3，某高新技术开发区有一个平行四边形的公园ABCD ，6AB BC +=千米，60ABC ∠=︒，公园内有一个儿童游乐场E ，分别从A 、B 、C 向游乐场E 修三条,,AE BE CE ，求三条路的长度和（即AE BE CE ++）最小时，平行四边形公园ABCD 的面积．【答案】（1）等边三角形；（2）BC 的最小值为52；（3）平行四边形公园ABCD 的面积为932（平方米）．【分析】（1）由旋转得BN =BM ，∠MBN =60°，可判断出△BMN 是等边三角形即可；（2）设AB =a ，则AC=10-a ，进而根据勾股定理得出()222550BC a =-+即可得出结论； （3）先判断出点A'，E'，E ，C 在同一条线上，设BF =x ，进而依次得出AB =2x ，BC =6-2x ，CF =6-x ，再利用勾股定理得出223'4()272A C x =-+，得出x =32是A'C 最小，进而求出A'F ，BC ，利用平行四边形面积公式计算即可．【详解】（1）证明：BMN △的形状是等边三角形，理由如下; 由旋转知，BN =BM ，∠MBN =60° ∴△BMN 为等边三角形 故答案为：等边三角形；（2）解：设AB =a ， ∵AB +AC =10， ∴AC =10-AB =10a -，在Rt △ABC 中，根据勾股定理得， ()2222210BC AB AC a a =+=+- 2220100a a =-+()22550a =-+， ∵()250a -≥，∴()2255050a -+≥，即250BC ≥， ∴52BC ≥，即BC 的最小值为52； （3）解：如图3，将△ABE 绕点B 逆时针旋转60°得到△A'BE'， ∴△ABE ≌△A'BE'，∴∠A'E'B =∠AEB ，AB =A'B ，A'E'=AE ，BE'=BE ，∠EBE'=60°， ∴△EBE'为等边三角形， ∴∠BE'E =∠BEE'=60°，EE'=BE ， ∴AE +BE +CE =A'E '+EE'+CE ，要AE +BE +CE 最小，即点A'，E'，E ，C 在同一条线上，即最小值为A'C ， 过点A '作A'F ⊥CB ，交CB 的延长线于F ， 在Rt △A'FB 中，∠A'BF =180°-∠ABA'-∠ABC =60°， 设BF =x ，则A'B =2x ， 根据勾股定理得，A'F =3x ， ∵AB =A'B ， ∴AB =2x ， ∵AB +BC =6， ∴BC =6-AB =6-2x ， ∴CF =BF +BC =6-x ，在Rt △A'FC 中，根据勾股定理得，2222223''3(6)4()272A C A F CF x x x =+=+-=-+，∴当x =32，即AB =2x =3时，2'A C 最小，此时，BC =6-3=3，A'F =3332x =， ∴平行四边形公园ABCD 的面积为3393322⨯=（平方千米）． 【点睛】本题是四边形综合题，主要考查了等边三角形的判定和性质，旋转的性质，勾股定理，用代数式表示线段，利用配方法确定极值问题，判断出AB =BC 时，AE +BE +CE 最小是解本题的关键． 11．在正方形ABCD 中，点E 为对角线AC （不含点A ）上任意一点，AB=22 （1）如图1，将△ADE 绕点D 逆时针旋转90°得到△DCF ，连接EF ；①把图形补充完整（无需写画法）；②求2EF的取值范围；(2)如图2，求BE+AE+DE的最小值．【答案】（1）①补图见解析；②2+≤≤；（2）232EF816【分析】（1）①根据要求画出图形即可；②首先证明∠ECF＝90°，设AE＝CF＝x，EF2＝y，则EC＝4−x，在Rt△ECF中，利用勾股定理即可解决问题；（2）如图2中，将△ABE绕点A顺时针旋转60°得到△AFG，连接EG，DF．作FH⊥AD于H．根据两点之间线段最短可得DF≤FG＋EG＋DE，BE＝FG，推出AE＋BE＋DE的最小值为线段DF的长；【详解】（1）①如图△DCF即为所求；②∵四边形ABCD是正方形，∴BC＝AB＝22，∠B＝90°，∠DAE＝∠ADC＝45°，∴AC＝22+＝2AB＝4，AB BC∵△ADE绕点D逆时针旋转90°得到△DCF，∴∠DCF＝∠DAE＝45°，AE＝CF，∴∠ECF＝∠ACD＋∠DCF＝90°，设AE＝CF＝x，EF2＝y，则EC＝4−x，∴y＝（4−x）2＋x2＝2x2−8x＋160（0＜x≤4）．即y＝2（x−2）2＋8，∵2＞0，∴x＝2时，y有最小值，最小值为8，当x ＝4时，y 最大值＝16， ∴8≤EF 2≤16．（2）如图中，将△ABE 绕点A 顺时针旋转60°得到△AFG ，连接EG ，DF ．作FH ⊥AD 于H ．由旋转的性质可知，△AEG 是等边三角形， ∴AE ＝EG ，∵DF≤FG ＋EG ＋DE ，BE ＝FG ，∴AE ＋BE ＋DE 的最小值为线段DF 的长． 在Rt △AFH 中，∠FAH ＝30°，AB ＝22=AF ， ∴FH ＝12AF ＝2，AH ＝22AF FH -＝6， 在Rt △DFH 中，DF ＝()2222(226)2FH DH +=++＝232+，∴BE ＋AE ＋ED 的最小值为232+．【点睛】本题考查作图−旋转变换，正方形的性质，勾股定理，两点之间线段最短等知识，解题的关键是学会构建二次函数解决最值问题，学会利用旋转法添加辅助线，学会用转化的思想思考问题，属于中考常考题型．12．如图1，点M 为锐角三角形ABC 内任意一点，连接,,AM BM CM ．以AB 为一边向外作等边三角形ABE △，将BM 绕点B 逆时针旋转60︒得到BN ，连接EN ．（1）求证：AMB ENB △≌△；（2）若AM BM CM ++的值最小，则称点M 为ABC 的费马点．若点M 为ABC 的费马点，求此时,,AMB BMC CMA ∠∠∠的度数；（3）受以上启发，你能想出作锐角三角形的费马点的一个方法吗？请利用图2画出草图，并说明作法以及理由．【答案】（1）见解析；（2）120BMC ∠=︒：120AMB ∠=︒；120AMC ∠=︒；（3）见解析 【分析】（1）结合等边三角形的性质，根据SAS 可证△AMB ≌△ENB（2）连接MN ，由（1）的结论证明ΔBMN 为等边三角形，所以BM =MN ，即AM+BM+CM =EN+MN+CM ，所以当E 、N 、M 、C 四点共线时，AM+BM+CM 的值最小，从而可求此时∠AMB 、∠BMC 、ΔCMA 的度数；（3）根据（2）中费马点的定义，又△ABC 的费马点在线段EC 上，同理也在线段BF 上，因此线段EC 和BF 的交点即为△ABC 的费马点．【详解】解：（1）证明：∵ABE △为等边三角形， ∴,60AB BE ABE =∠=︒． 而60MBN ∠=︒， ∴ABM EBN ∠=∠． 在AMB 与ENB △中，AB BE ABM EBN BM BN =⎧⎪∠=∠⎨⎪=⎩∴(SAS)AMB ENB ≌．（2）连接MN ．由（1）知，AM EN =． ∵60,MBN BM BN ∠=︒=， ∴BMN △为等边三角形． ∴BM MN =．∴AM BM CM EN MN CM ++=++．∴当E 、N 、M 、C 四点共线时，AM BM CM ++的值最小．此时，180120BMC NMB ∠=︒-∠=︒：180120AMB ENB BNM ∠=∠=︒-∠=︒；︒︒．∠=-∠-∠=AMC BMC AMB360120CE BF，相（3）如图2，分别以ABC的AB，AC为一边向外作等边ABE△和等边ACF，连接,交于M，则点M即为ABC的费马点，由（2）知，ABC的费马点在线段EC上，同理也在线段BF 上．因此线段EC与BF的交点即为ABC的费马点．（方法不唯一，正确即可）【点睛】本题考查了等边三角形的性质，三角形全等的判定与性质,掌握三角形全等的判定和性质是解题的关键．13．若点P为△ABC所在平面上一点，且∠APB＝∠BPC＝∠CP A＝120°，则点P叫做△ABC的费马点．当三角形的最大角小于120°时，可以证明费马点就是“到三角形的三个顶点的距离之和最小的点“．即P A+PB+PC最小．（1）如图1，向△ABC外作等边三角形△ABD，△AEC．连接BE，DC相交于点P，连接AP．①证明：点P就是△ABC费马点；②证明：P A+PB+PC＝BE＝DC；（2）如图2，在△MNG中，MN＝2，∠M＝75°，MG＝3．点O是△MNG内一点，则点O到△MNG 三个顶点的距离和的最小值是．【答案】（1）①证详见解析；②详见解析；（2）65．【分析】（1）①如图1﹣1中，作AM⊥CD于M，AN⊥BE于N设AB交CD于O．证明△ADC ≌△ABE（SAS）即可解决问题．②在线段PDA上取一点T，使得PA＝PT，连接AT．证明△DAT≌△BAP（SAS），推出PD＝PA+PB 即可解决问题．（2）以MG为边作等边三角形△MGD，以OM为边作等边△OME．连接ND，可证△GMO≌△DME，可得GO＝DE，则MO+NO+GO＝NO+OE+DE，即当D、E、O、N四点共线时，MO+NO+GO值最小，最小值为ND的长度，根据勾股定理先求得MF、DF，然后求ND的长度，即可求MO+NO+GO 的最小值．【详解】（1）①如图1﹣1中，作AM⊥CD于M，AN⊥BE于N设AB交CD于O．∵△ADB，△ACE都是等边三角形，∴AD＝AB，AC＝AE，∠DAB＝∠CAE＝60°，∴∠DAB＝∠BAE，∴△ADC≌△ABE（SAS），∴CD＝BE，S△DAC＝S△ABE，∠ADC＝∠ABE，∵AM⊥CD，AN⊥BE，∴12•CD•AM＝12•BE•AN，∴AM＝AN，∴∠APM＝∠APN，∵∠AOD＝∠POB，∴∠OPB＝∠DAO＝60°，∴∠APN＝∠APM＝60°，∴∠APC＝∠BPC＝∠APC＝120°，∴点P是就是△ABC费马点．②在线段PDA上取一点T，使得PA＝PT，连接AT．∵∠APT＝60°，PT＝PA，∴△APT是等边三角形，∴∠PAT＝60°，AT＝AP，∵∠DAB＝∠TAP＝60°，∴∠DAT＝∠BAP，∵AD＝AB，∴△DAT≌△BAP（SAS），∴PB＝DT，∴PD＝DT+PT＝PA+PB，∴PA+PB+PC＝PD+PC＝CD＝BE．（2）如图2：以MG为边作等边三角形△MGD，以OM为边作等边△OME．连接ND，作DF⊥NM，交NM的延长线于F．∵△MGD和△OME是等边三角形∴OE＝OM＝ME，∠DMG＝∠OME＝60°，MG＝MD，∴∠GMO＝∠DME在△GMO和△DME中，OM MEGMO DMEMG MD=⎧⎪∠=∠⎨⎪=⎩，∴△GMO≌△DME（SAS），∴OG＝DE∴NO+GO+MO＝DE+OE+NO∴当D、E、O、M四点共线时，NO+GO+MO值最小，∵∠NMG＝75°，∠GMD＝60°，∴∠NMD＝135°，∴∠DMF＝45°，∵MG＝3∴MF ＝DF ＝322， ∴NF ＝MN+MF ＝43222+＝1122， ∴ND ＝22NF DF +＝221123222⎛⎫⎛⎫+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭＝65，∴MO+NO+GO 最小值为65， 故答案为65，【点睛】本题属于三角形综合题，考查了旋转的性质，等边三角形的性质，勾股定理，最短路径问题，构造等边三角形是解答本题的关键．14．如图，在ABC 中，30,6,5ACB BC AC ∠=︒==，在ABC 内部有一点P ，连接PA 、PB 、PC ．（加权费马点）求：（1）PA PB PC ++的最小值； （2）2PA PB PC +的最小值 （3）3PA PB PC +的最小值； （4）23PA PB PC +的最小值 （5）132PA PB ++的最小值；（6）2423PA PB PC ++的最小值 （7）4223PA PB PC ++的最小值； （8）345PA PB PC ++的最小值【答案】（1）61；（2）91；（3）61303+；（4）234；（5）132；（6）26；（7）434；（8）214【分析】（1）将BPC △绕点B 顺时针旋转60得到BP C ''△，则BP BP '=，P C PC '=，60PBP '∠=，可以推出BPP '为等边三角形，得到BP PP '=，则PA PB PC PA PP PC ''++=++，即可得到A 、P 、P '、C '四点共线时，PA PB PC ++最小，最小值为AC '，然后证明==90ACC ACB BCC ''+∠∠∠，由此利用勾股定理求解即可；（2）将BPC △绕点C 逆时针旋转90得到CP B ''△，则可证明2PP PC '=，从而得到2PA PB PC PA PP P B ''++=++，则当A 、P 、P '、B '四点共线时PA PB PC ++最小，最小值为AB '，过点A 再作B C '的垂线，垂足为E ，利用勾股定理求出22532AE AC CE =-=，172B E B C EC ''=+=，由此即可得到答案；（3）将BPC △绕点C 逆时针旋转120得到B PC ''△，则可证明3PP CP '=，则3PA PB PC PA PP P B '''++=++，故当A 、P 、P '、B '四点共线时3PA PB PC ++最小，最小值为AB '，过点A 再作B C '的垂线，垂足为E ，利用勾股定理求出22532CE AC AE =-=，12532B E CE CB +''=+=，由此即可得到答案； （4）将BPC △绕点C 顺时针旋转60，得到CP A ''，再将CP A ''以点C 为位似中心放大2倍，得到CP A ''''，连接PP '，先证明3P P CP ''=，则可以得到23PA PB PC A P P P PB ''''''++=++，故当A ''，P ''，P ，B 共线时23PA PB PC ++最小，最小为A B ''，然后证明=90BCA ACB ACA ''''=+∠∠∠，即可利用勾股定理求解；（5）将BPC △绕点C 顺时针旋转60，得到CP A ''，再将CP A ''以点C 为位似中心缩小2倍，得到CP A ''''，同（4）原理可证得当A ''，P ''，P ，B 共线时1322PA PB PC ++最小，最小为A B ''，然后证明=90BCA ACB ACA ''''=+∠∠∠，由此求解即可；（6）由132423422PA PB PC PA PB PC ⎛⎫++=++ ⎪ ⎪⎝⎭可由（5）得：2423PA PB PC ++的最小值为26；（7）由42232(23)PA PB PC PA PB PC ++=++可由（4）得4223PA PB PC ++的最小值为434；（8）将BPC △绕点C 顺时针旋转90，得到CP A ''，再将CP A ''以点C 为位似中心缩小34倍，得到CP A ''''，同理可以证得当A 、P 、P ''、A ''，共线时345PA PB PC ++的值最小．在BCA ''中，120BCA ACB ACA ''∠=+'='∠∠，31544A C CA ==''，过点A ''作A E BC ''⊥交BC 延长线于E ，然后求出EA ''，BE 的长，由此即可求解．【详解】解：（1）如图3-2，将BPC △绕点B 顺时针旋转60得到BP C ''△， ∴BP BP '=，P C PC '=，60PBP '∠=， ∴BPP '为等边三角形， ∴BP PP '=，∴PA PB PC PA PP PC ''++=++，∴A 、P 、P '、C '四点共线时，PA PB PC ++最小，最小值为AC '同理可证BCC '为等边三角形， ∴6CC BC '==，=60BCC '∠， ∴==90ACC ACB BCC ''+∠∠∠， ∴2261AC AC CC ''=+=； ∴PA PB PC ++的最小值为61；（2）如图3-4，将BPC △绕点C 逆时针旋转90得到CP B ''△，∴B P BP ''=，P C PC '=，90PCP '=∠，=P CB PCB ''∠∠，6CB CB '==， ∴222PP PC P C PC ''=+=， ∴2PA PB PC PA PP P B ''++=++，∴当A 、P 、P '、B '四点共线时，PA PB PC ++最小，最小值为AB ' ∵∠ACB =30°，∴=30ACP PCB ACP P CB ''∠+∠=∠+∠ ∴120ACB PCP ACP P CB ''''∠=∠+∠+∠=， 过点A 再作B C '的垂线，垂足为E ， ∴∠AEC =90°，∠ACE =60°， ∴∠CAE =30°， ∴1522CE AC == ∴22532AE AC CE =-=，172B E B C EC ''=+=，∴2291AB AE B E ''=+=， ∴2PA PB PC ++的最小值为91；（3）如图3-6，将BPC △绕点C 逆时针旋转120得到B PC ''△，∴B P BP ''=，P C PC '=，120PCP '=∠，=P CB PCB ''∠∠，6CB CB '==， ∴30CPP CP P ''==∠∠， 过点C 作CE PP '⊥于E ，∴12CE CP =，PE P E '=，∴2232PE PC CE CP =-=， ∴3PP CP '=，∴3PA PB PC PA PP P B '''++=++，∴当A 、P 、P '、B '四点共线时，3PA PB PC ++最小，最小值为AB ' ∵∠ACB =30°，∴=30ACP PCB ACP P CB ''∠+∠=∠+∠ ∴==150ACB PCP ACP P CB ''''++∠∠∠∠， 过点A 再作B C '的垂线，垂足为E ， ∴∠AEC =90°，∠ACE =3°， ∴1522AE AC == ∴22532CE AC AE =-=， ∴12532B E CE CB +''=+=∴2261303AB AE B E '=+'=+， ∴3PA PB PC ++的最小值为61303+；（4）如图3-8，将BPC △绕点C 顺时针旋转60，得到CP A ''，再将CP A ''以点C 为位似中心放大2倍，得到CP A ''''，连接PP '由旋转的性质得5CA CA '==，CP CP '=，PA P A ''=，==60PCP ACA ''∠∠，∴10CA ''=，2CP CP ''=，22P A A P AP '''=='''，PCP '△是等边三角形，∴PP P C P P '''''==，=60PP C '∠，∴==30PP P P PP '''''∠∠，∴=90P PC ''∠，∴223P P CP CP CP ''''=-=，∴23PA PB PC A P P P PB ''''''++=++，∴当A ''，P ''，P ，B 共线时23PA PB PC ++最小，最小为A B ''，∵=90BCA ACB ACA ''''=+∠∠∠，∴22234A B BC A C ''''=+=，∴23PA PB PC ++的最小值为234；（5）如图3-10，将BPC △绕点C 顺时针旋转60，得到CP A ''，再将CP A ''以点C 为位似中心缩小2倍，得到CP A ''''，同（4）原理可证得当A ''，P ''，P ，B 共线时1322PA PB PC ++最小，最小为A B ''，∵=90BCA ACB ACA ''''=+∠∠∠，在Rt BCA ''中，6BC =，15=22CA CA '=' 22132BC BA A C ''=+=''， 1322PA PB PC ++最小为132； （6）∵132423422PA PB PC PA PB PC ⎛⎫++=++ ⎪ ⎪⎝⎭∴由（5）得：2423PA PB PC ++的最小值为26；（7）∵42232(23)PA PB PC PA PB PC ++=++∴由（4）得4223PA PB PC ++的最小值为434；（8）如图3-12，将BPC △绕点C 顺时针旋转90，得到CP A ''，再将CP A ''以点C 为位似中心缩小34倍，得到CP A ''''， 同理可以证得当A 、P 、P ''、A ''，共线时345PA PB PC ++的值最小．在BCA ''中，120BCA ACB ACA ''∠=+'='∠∠，31544A C CA ==''， 过点A ''作A E BC ''⊥交BC 延长线于E ，∴60A CE ∠=''，∴30CA E ∠=''，∴115=28CE CA ''=， ∴22153=8EA A C CE ''=-''，1568BE BC CE =+=+， ∴22221515321=6884BA A E BE ⎛⎫⎛⎫''=+++= ⎪ ⎪⎝⎭⎝⎭''， 345PA PB PC ++的最小值为214．【点睛】本题主要考查了旋转的性质，勾股定理，位似，含30度角的直角三角形的性质，等边三角形的性质与判定，等腰三角形的性质与判定等等，解题的关键在于能够作出辅助线，找到P点在什么位置时，线段的和最小．。

旋转模型专题一、等线段共点二、按图形分类1、等腰三角形，2、等边三角形，3、等腰直角三角形，4、正方形三、按模型分类1、手拉手模型2、角含半角模型3、对角互补模型4、与勾股定理结合5、费马点问题例题精讲等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形ABCD一、手拉手模型常见共顶点（手拉手）模型结论 （请自行证明）1.共顶点等边三角形 结论：(1)△BCD △△ACE(2)BD =AE(3)△AFB =60° (4)FC 平分△BFE (5)FB =F A +FC ；FE =FD +FC2.共顶点等腰直角三角形形 结论：(1)△BCD △△ACE(2)BD =AE (3)△AFB =90°(4)FC 平分△BFE(5)FB =F AFC ；FE =FD(6)2222AE BD AD BE +=+ (7) ACD BCE S S =△△(8)I 是AD 中点，则CI △BE ，CI =12BE1、如图，在凸四边形ABCD 中，30BCD ∠=︒,60DAB AD AB ∠=︒=，． 求证：222AC CD BC =+2.等边三角形ABC 有一点P ，PA =3，PB =5，PC =4，求∠APC 的度数.3内有一点P ，且PA =PB =4，PC =2，则∠BPC 的度数为______，正六边形ABCDEF 的边长为_____.BB③②①AH CBDDCBADCBA4、已知ABC ∆，以AC 为边在ABC ∆外作等腰ACD ∆，其中AC AD =。

⑴如图①，若2DAC ABC ∠=∠，AC BC =，四边形ABCD 是平行四边形，则_____ABC ∠= ⑵如图②，若30ABC ∠=︒，ACD ∆是等边三角形，3AB =，4BC =，求BD 的长； ⑶如图③，若ACD ∠为锐角，作AH BC ⊥于H ，当2224BD AH BC =+时，2DAC ABC ∠=∠是否成立？若不成立，请说明你的理由；若成立，证明你的结论。

专题07 双等腰旋转模型【模型说明】【例题精讲】例1．（基本模型）在V ABC 中，AB =AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作V ADE ，使AD =AE ，∠DAE =∠BAC ，连接CE ．（1）如图1，当点D 在线段BC 上，如果∠BAC =90°，则∠BCE = 度； （2）设BAC a Ð=，BCE b Ð=．①如图2，当点在线段BC 上移动，则a ，b 之间有怎样的数量关系？请说明理由；②当点在直线BC 上（线段BC 之外）移动，则a ，b 之间有怎样的数量关系？请直接写出你的结论．【答案】（1）90；（2）180a b +=°，见解析；②180a b +=°或a b=【详解】解：（1）∵90BAC Ð=°，∴90DAE BAC Ð=Ð=°，∵AB =AC ，AD =AE ，∴45B ACB Ð=Ð=°，45ADE AED Ð=Ð=°，∵DAE BAC Ð=Ð，∴BAD CAE Ð=Ð，在BAD V 和CAE V 中BAD CAEAD AE ïÐ=Ðíï=î\BAD CAE @V V ，∴45ACE B Ð=Ð=°，∴90BCE ACB ACE Ð=Ð+Ð=°（2）αβ180+=°或a b =．理由：①∵BAC DAE Ð=Ð，∴BAC DAC DAE DAC Ð-Ð=Ð-Ð．即BAD CAE Ð=Ð．在BAD V 和CAE V 中AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴ABD ACE △≌△．∴B ACE Ð=Ð．∴B ACB ACE ACB Ð+Ð=Ð+Ð．∴B ACB b Ð+Ð=．∵180B ACB a +Ð+Ð=°，∴180a b +=°．②如图：∵BAC DAE Ð=Ð，∴BAC BAE DAE BAE Ð-Ð=Ð-Ð．即BAD CAE Ð=Ð．在BAD V 和CAE V 中BAD CAE AD AE ïÐ=Ðíï=î，∴ABD ACE △≌△． ∴ABD ACE Ð=Ð．∵+ABD ACB a Ð=Ð，ACE ACB b =Ð-Ð，ACE ABD b a \=Ð-Ð+，a b \=．综上所述：点D 在直线BC 上移动，α+β＝180°或α＝β．例2．（坐标系综合）已知：平面直角坐标系中，点A 在y 轴的正半轴上，点B 在第二象限，将OB 绕O 点顺时针转60°至OA ．（1）如图1，试判定△ABO 的形状，并说明理由．（2）如图1，若点E 为y 轴的正半轴上一动点，以BE 为边作等边△BEG ，延长GA 交x 轴于点P ，问：AP 与AO 之间有何数量关系，试证明你的结论．（3）如图2，若BC ⊥BO ，BC ＝BO ，作BD ⊥CO ，AC 、DB 交于E ，补全图形，并证明：AE ＝BE+CE ．【答案】（1）等边三角形，理由见解析；（2）AP ＝2AO ，证明见解析；（3）见解析【详解】解：（1）如图1，△AOB 为等边三角形，理由是：∵将绕OB 绕O 点旋转至OA ∴∠AOB=60°，∵AO ＝AB∴△AOB 为等边三角形；（2）AP ＝2AO ，理由为：证明：∵△AOB 与△BGE 都为等边三角形，∴BE ＝BG ，AB ＝OB ，∠EBG ＝∠OBA ＝60°，∴∠EBG+∠EBA ＝∠OBA+∠EBA ，即∠ABG ＝∠OBE ，在△ABG 和△OBE 中，BE BG ABG OBEAB OB =ìïÐ=Ðíï=î∴△ABG ≌△OBE （SAS ），∴∠BAG ＝∠BOE ＝60°，∴∠GAO ＝∠GAB+∠BAO ＝120°，∵∠GAO 为△AOP 的外角，且∠AOP ＝90°，∴∠APO ＝30°在Rt △AOP 中，∠APO ＝30°，则AP ＝2AO ．（3）补全图形，在AC 上截取AM ＝EC ，连接BM ，可得AM+EM ＝CE+EM ，即AE ＝CM ，∵△AOB 为等边三角形，△BOC 为等腰直角三角形，∴∠OBC ＝90°，∠ABO ＝60°，∵D 为CO 的中点，∴BD 平分∠OBC ，即∠CBD ＝∠OBD ＝45°，∴∠ABD ＝105°，∠ABC ＝150°，∴∠BAC ＝∠BCA ＝15°，∴∠AEB ＝15°+45°＝60°，在△ABE 和△CBM 中，∵AB CB BAE BCMAE CM =ìïÐ=Ðíï=î∴△ABE ≌△CBM （SAS ），∴BM ＝BE ，∴△BEM 为等边三角形，∴BE ＝EM ，∴AE ＝AM+EM ＝CE+BE ；例3．（培优综合）在Rt △ABC 中，∠ACB ＝90°，CA ＝CB ，点D 是直线AB 上的一点，连接CD ，将线段CD 绕点C 逆时针旋转90°，得到线段CE ，连接EB ．（1）操作发现如图1，当点D 在线段AB 上时，请你直接写出AB 与BE 的位置关系为 ；线段BD 、AB 、EB 的数量关系为 ；（2）猜想论证当点D 在直线AB 上运动时，如图2，是点D 在射线AB 上，如图3，是点D 在射线BA 上，请你写出这两种情况下，线段BD 、AB 、EB 的数量关系，并对图2的结论进行证明；（3）拓展延伸若AB ＝5，BD ＝7，请你直接写出△ADE 的面积．【答案】（1）AB ⊥BE，AB＝BD +BE ；（2）图2中BE ＝AB +BD ，图3中，BD ＝AB +BE ，证明见解析；（3）72或2【详解】解：（1）如图1中，∵∠ACB ＝∠DCE ＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS），∴AD＝BE，∠CBE＝∠A，∵CA＝CB，∠ACB＝90°，∴∠A＝∠CBA＝45°，∴∠CBE＝∠A＝45°，∴ABE＝90°，∴AB⊥BE，∵AB＝AD+BD，AD＝BE，∴AB＝BD+BE，故答案为AB⊥BE，AB＝BD+BE．（2）①如图2中，结论：BE＝AB+BD．理由：∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS），∴AD＝BE，∵AD＝AB+BD，AD＝BE，∴BE＝AB+BD．②如图3中，结论：BD＝AB+BE．【课后作业】1．如图，在ABC V 中，(),060AB AC BAC a a =Ð=°<<°，点D 在ABC V 内，BD BC =，60DBC Ð=°，点E在ABC V 外，150,60ECB ABE Ð=Ð=°°．(1)ADB Ð的度数为_______________；(2)小华说ABE △是等腰三角形，小明说ABE △是等边三角形，___________的说法更准确，并说明理由；(3)连接DE ，若,10^=DE BD DE ，求AD 的长．∵∠BCE=150°，∠DCB=60° ∴∠DCE=90°，∵∠EDB=90°，∠BDC=60° ，∴∠EDC=30° ，∴152EC DE==．∵△ABD≌△EBC，∴AD=求证：AH=12BC．[拓展]：（2）如图2．在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE=90°，点D、B、C在同一条直线上，AH为△ABC中BC边上的高，连接CE．则∠DCE的度数为________，同时猜想线段AH、CD、CE之间的数量关系，并说明理由．[应用]：（3）在图3、图4中．在△ABC中，AB=AC，且∠BAC=90°，在同一平面内有一点P，满足PC=1，PB=6，且∠BPC=90°，请求出点A到BP的距离．AD 的右侧作ADE V ，使AD AE =，DAE BAC Ð=Ð，连接CE ．（1）如图，当点D 在线段BC 上，如果90BAC Ð=°，则BCE Ð=______度．（2）设BAC a Ð=，BCE b Ð=．①如图，当点D 在线段BC 上移动时，a 、b 之间有怎样的数量关系？请直接写出你的结论．②如图，当点D 在线段BC 的反向延长线上移动时，a 、b 之间有怎样的数量关系？请说明理由．【答案】（1）90；（2）①180a b +=°，理由见解析；②a b =，理由见解析【详解】（1）∵AB=AC ，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠DAE=∠BAC ，∴∠BAD=∠CAE ，在△BAD 和△CAE 中AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴△BAD ≌△CAE （SAS ）∴∠ABC=∠ACE=45°，∴∠BCE=∠ACB+∠ACE=90°，故答案为：90；（2）①180a b +=°．理由：∵∠BAC=∠DAE ，∴∠BAC-∠DAC=∠DAE-∠DAC ．即∠BAD=∠CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴△ABD ≌△ACE （SAS ），∴∠B=∠ACE ．∴∠B+∠ACB=∠ACE+∠ACB ．∵∠ACE+∠ACB=β，∴∠B+∠ACB=β，∵α+∠B+∠ACB=180°，∴α+β=180°；② 当点D 在射线BC 的反向延长线上时，a b =．理由如下：∵DAE BAC Ð=Ð，∴DAB EAC Ð=Ð，在△ABD 与△ACE 中，AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴△≌△ADB AEC (SAS)，∴ABD ACE Ð=Ð，∵ABD BAC ACB Ð=Ð+Ð，ACE BCE ACB Ð=Ð+Ð，∴BAC ABD ACB Ð=Ð-Ð，BCE ACE ACB Ð=Ð-Ð，∴BAC BCE Ð=Ð，即a b =．4．（1）如图①，在直角ABC V 中，90BAC Ð=°，AB AC =，点D 为BC 边上一动点（与点B 不重合），连接AD ，将ABD △绕点A 逆时针旋转90°，得到ACE V ，那么,CE BD 之间的位置关系为__________，数量关系为__________；（2）如图②，在ABC V 中，90BAC Ð=°，AB AC =，D ，E （点D ，E 不与点B ，C 重合）为BC 上两动点，且45DAE Ð=°．求证：222BD CE DE +=．（3）如图③，在ABC V 中，120CAB Ð=°，AB AC =，60DAE Ð=°，3BC =+D ，E （点D ，E 不与点B ，C 重合）为BC 上两动点，若以,,BD DE EC 为边长的三角形是以BD 为斜边的直角三角形时，求BE 的长．∴ABD ACED @D ∴ACE 45B Ð=Ð=°且CE=BD∵ACB 45B Ð=Ð=°∴ECB=4545=90а+°°，即CE ⊥BD故答案为：CE ⊥BD ；CE=BD ；（2）如图②，把ACE D 绕点A 顺时针旋转90°，得到ABG D ，连接DG ，则ACE ABGD @D ∴AG=AE ，BG=CE ，ABG ACF 45Ð=Ð=°∵BAC 90Ð=°，GAE 90Ð=°∴GAD DAE 45Ð=Ð=°在ADG D 和ADE D 中，AG AE GAD DAEAD AD =ìïÐ=Ðíï=î∴ADG ADED @D ∴ED=GD∵GBD 90Ð=°∴222BD BG DG +=即222BD EC DE +=（3）如图③，把AEC D 绕点A 顺时针旋转120°，得到AFB D ，∴AEC AFBD @D ∴AF=AE ，ABF ACB Ð=Ð，EC=BF ，EAF 120Ð=°∵CAB 120Ð=°，AB=AC∴ABC ACB ABF 30Ð=Ð=Ð=°。

专题3.1 旋转重难点模型（5大类型）【题型1 手拉手模型】【题型2 “半角”模型】【题型3 构造旋转模型解题】【题型4 奔驰模型】【题型5 费马点模型】模型一：“手拉手”模型模型特征：两个等边三角形或等腰直角三角形或正方形共顶点。

模型说明：如图1，▲ABE，▲ACF都是等边三角形，可证▲AEC≌▲ABF。

如图2，▲ABD，▲ACE都是等腰直角三角形，可证▲ADC≌▲ABE如图2，四边形ABEF，四边形ACHD都是正方形，可证▲ABD≌▲AFC模型二：“半角”模型模型特征：大角含半角+有相等的边，通过旋转“使相等的边重合，拼出特殊角”模型说明：（1）如图，在正方形ABCD中，∠EAF=45°，将▲ADF绕点A顺时针旋转90°，得到▲ABG 可证▲AEF≌AEG，所以可到DF+BE=EF（2）如图，在等腰直角▲ABC中，∠MAN=45°，将▲ACN绕点A顺时针旋转90°，得到▲ABQ，可证▲AMN≌▲AMQ，所以可得CN²+BM²=MN²（3）如图，等腰▲ABC中，AB=BC，∠DBE=将▲CBD绕点B逆时针旋转∠CBA 的度数得到▲ABD’可证▲DBE≌▲D’BE。

模型三：构造旋转模型解题方法指导：若一个图形中含有相等的线段和特殊的角度，通常是以等线段的公共端点为旋转中心进行旋转，使得相等的边重合，得出特殊的图形.常见图形旋转：方法归纳：将等边三角形内的一个小三角形，旋转60度，从而使小三角形的一边与原等边三角形的边重合，连接小三角形的钝角顶点，得三角形．通过旋转将不相关的线段转化到同一个三角形中，将分散的已知条件集中起来，使问题得以解决．模型四：奔驰模型模型五：费马点模型【费马点问题】问题：如图1，如何找点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？图文解析：如图1，把△APC绕C点顺时针旋转60°得到△A′P′C，连接PP′．则△CPP′为等边三角形，CP=PP′，PA=P′A′，△PA+PB+PC= P′A′+PB+PP′BC′．△点A′可看成是线段CA绕C点顺时针旋转60°而得的定点，BA′为定长△当B、P、P′、A′ 四点在同一直线上时，PA+PB+PC最小．最小值为BA.′【典例1】（2022春•西安期末）如图，在△ABC中，BC＝5，以AC为边向外作等边△ACD，以AB为边向外作等边△ABE，连接CE、BD．（1）若AC＝4，∠ACB＝30°，求CE的长；（2）若∠ABC＝60°，AB＝3，求BD的长．【变式11】（2022秋•荔湾区校级期中）以△ABC的AB，AC为边分别作正方形ADEB，正方形ACGF，连接DC，BF．（1）CD与BF有什么数量与位置关系？说明理由．（2）利用旋转的观点，在此题中，△ADC可看成由哪个三角形绕哪点旋转多少角度得到的．【变式12】（2022九上·吉林期末）如图①，在△ABC中，∠C=90°，AC=BC=√6，点D，E分别在边AC，BC上，且CD=CE=√2，此时AD=BE，AD⊥BE成立．（1）将△CDE绕点C逆时针旋转90°时，在图②中补充图形，并直接写出BE的长度；（2）当△CDE绕点C逆时针旋转一周的过程中，AD与BE的数量关系和位置关系是否仍然成立？若成立，请你利用图③证明，若不成立请说明理由；（3）将△CDE绕点C逆时针旋转一周的过程中，当A，D，E三点在同一条直线上时，请直接写出AD的长度．【典例2】（秋•锦江区期末）在△ABC中，AB＝AC，点E，F是边BC所在直线上与点B，C不重合的两点．（1）如图1，当∠BAC＝90°，∠EAF＝45°时，直接写出线段BE，CF，EF的数量关系；（不必证明）（2）如图2，当∠BAC＝60°，∠EAF＝30°时，已知BE＝3，CF＝5，求线段EF的长度；（3）如图3，当∠BAC＝90°，∠EAF＝135°时，请探究线段CE，BF，EF的数量关系，并证明．【变式21】（春•金牛区校级期中）类比探究：（1）如图1，等边△ABC内有一点P，若AP＝8，BP＝15，CP＝17，求∠APB的大小；（提示：将△ABP绕顶点A旋转到△ACP′处）（2）如图2，在△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点，且∠EAF＝45°．求证：EF2＝BE2+FC2；（3）如图3，在△ABC中，∠C＝90°，∠ABC＝30°，点O为△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，若AC＝1，求OA+OB+OC的值．【变式22】（2022春•西山区校级月考）如图，已知正方形ABCD，点E、F分别是AB、BC边上，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．（1）求证：△EDF≌△MDF；（2）若正方形ABCD的边长为5，AE＝2时，求EF的长？【变式23】（2022秋•山西期末）阅读以下材料，并按要求完成相应的任务：从正方形的一个顶点引出夹角为45°的两条射线，并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型．半角模型可证出多个几何结论，例如：如图1，在正方形ABCD中，以A为顶点的∠EAF＝45°，AE、AF与BC、CD边分别交于E、F两点．易证得EF＝BE+FD．大致证明思路：如图2，将△ADF绕点A顺时针旋转90°，得到△ABH，由∠HBE＝180°可得H、B、E三点共线，∠HAE＝∠EAF＝45°，进而可证明△AEH≌△AEF，故EF＝BE+DF．任务：如图3，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，∠BAD＝120°，以A为顶点的∠EAF＝60°，AE、AF与BC、CD边分别交于E、F两点．请参照阅读材料中的解题方法，你认为结论EF＝BE+DF是否依然成立，若成立，请写出证明过程；若不成立，请说明理由．【典例3】（九上·江津期中）请阅读下列材料：问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB= √3，PC=1、求△BPC 度数的大小和等边三角形ABC的边长．李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以△AP′B=150°，而△BPC=△AP′B=150°，进而求出等边△ABC的边长为√7，问题得到解决．请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA= √5，BP= √2，PC=1．求△BPC度数的大小和正方形ABCD的边长．【变式31】（九上·南昌月考）如图，在等边三角形ABC内有一点P，且PA=2，PB=√3，PC=1，求∠BPC的度数和等边三角形ABC的边长．【变式32】（九上·德州期中）当图形具有邻边相等的特征时，我们可以把图形的一部分绕着公共端点旋转，这样将分散的条件集中起来，从而达到解决问题的目的．（1）如图1，等腰直角三角形ABC内有一点P，连接AP，BP，CP，△APB＝135°，为探究AP，BP，CP三条线段间的数量关系，我们可以将△ABP，绕点A逆时针旋转90°得到△ACP'，连接PP'，则PP'＝AP，△CPP'是三角形，AP，BP，CP三条线段的数量关系是．（2）如图2，等边三角形ABC内有一点P，连接AP、BP、CP，△APB＝150°，请借助第一问的方法探究AP、BP、CP三条线段间的数量关系．（3）如图3，在四边形ABCD中，AD△BC，点P在四边形的内部，且PD＝PC，△CPD ＝90°，△APB＝135°，AD＝4，BC＝5，请直接写出AB的长．【典例4】（2023•崂山区模拟）阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且P A＝3，PB＝4，PC＝5，求∠APB的度数．小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．请你回答：图1中∠APB的度数等于．参考小伟同学思考问题的方法，解决下列问题：（1）如图3，在正方形ABCD内有一点P，且P A＝，PB＝1，PD＝，则∠APB的度数等于，正方形的边长为；（2）如图4，在正六边形ABCDEF内有一点P，且P A＝2，PB＝1，PF＝，则∠APB的度数等于，正六边形的边．【变式41】（2023春•广东期中）18．如图，P是正三角形ABC内的一点，且P A＝6，PB＝8，PC＝10．若将△P AC绕点A逆时针旋转后，得到△MAB．（1）∠MAP＝°，连接PM，则PM＝；（2）求∠APB的度数．【变式42】（2023春•古田县期中）阅读材料，解决问题：（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为5，12，13，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段P A、PB、PC转化到一个三角形中，从而求出∠APB＝；（2）请你利用第（1）题的解答思想方法，解答下面问题，已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2．【变式44】（2022春•侯马市期末）如图①，△ABC和△ADE中，∠BAC＝∠DAE＝90°，点D、E分别在边AB、AC上，∠ABC＝∠ADE＝45°．（1）如图②，将△ADE绕点A逆时针旋转到如图位置，若∠BAD＝30°，求∠BAE的度数；（2）如图②，将△ADE绕点A逆时针旋转过程中，当旋转角度α＝时，直线AC与DE垂直（0°＜α≤360°）；（3）如图③，△ADE绕点A在平面内自由旋转，连接BD，且AD＝4，AB＝10，求BD的最大值和最小值．【典例5】（秋•邗江区期末）背景资料：在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图①，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB＝∠BPC＝∠CP A＝120°，此时，P A+PB+PC的值最小．解决问题：（1）如图②，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段P A，PB，PC转化到一个三角形中，从而求出∠APB＝；基本运用：（2）请你利用第（1）题的解答思想方法，解答下面问题：如图③，△ABC中，∠CAB＝90°，AB＝AC，E，F为BC上的点，且∠EAF ＝45°，判断BE，EF，FC之间的数量关系并证明；能力提升：（3）如图④，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点P为Rt△ABC的费马点，连接AP，BP，CP，求P A+PB+PC的值．【变式51】（2022秋•大冶市期末）如图，D是等边三角形ABC外一点，连接AD，BD，CD，已知BD＝8，CD＝3，则当线段AD的长度最小时，①∠BDC＝；②AD的最小值是．【变式52】（2022•荷塘区模拟）在△ABC中，若其内部的点P满足∠APB＝∠BPC＝∠CP A＝120°，则称P为△ABC的费马点．如图所示，在△ABC中，已知∠BAC＝45°，设P为△ABC的费马点，且满足∠PBA＝45°，P A＝4，则△P AC的面积为．。