西安电子考研 信号与系统第四版 答案

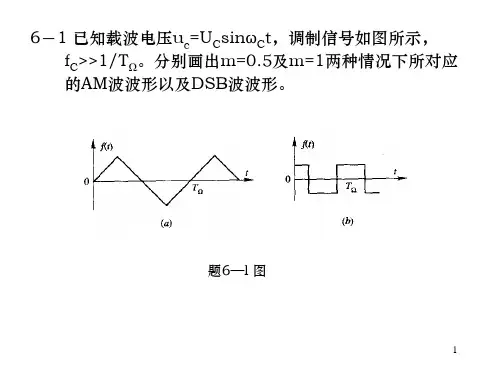
第七章 系统函数一、单项选择题X7.1（浙江大学2004考研题）一个因果、稳定的离散时间系统函数)(z H 的极点必定在z 平面的 。

（A ）单位圆以外 （B ）实轴上 （C ）左半平面 （D ）单位圆以内 H (s )只有一对在虚轴上的共轭极点，则它的h (t )应是 。

（A ）指数增长信号 （B ）指数衰减振荡信号 （C ）常数 （D ）等幅振荡信号 X7.3（浙江大学2003考研题）如果一离散时间系统的系统函数)(z H 只有一个在单位圆上实数为1的极点，则它的h (k )应是 。

（A ）ε(k ) （B ）)(k ε- （C ）)()1(k kε- （D ）1X7.4（浙江大学2002考研题）已知一连续系统的零、极点分布如图X7.4所示，1)(=∞H ，则系统函数H (s )为 。

（A ）2+s （B ）1+s （C ）)2)(1(++s s （D ）1-s X7.5（西安电子科技大学2004考研题）图X7.5所示信号流图的系统函数H (s )为 。

（A ）26132+++s s s （B ）2132++s s （C ）26132--+s s s （D ）1212-+s s X7.6（哈尔滨工业大学2002考研题）下列几个因果系统函数中，稳定（包括临界稳定）的系统函数有 个。

（1）4312+--s s s （2）s s s 312++ （3）34234+++s s s （4）33223++++s s s s （5）1224++s s s （6）2421ss + （A ）3 （B ）2 （C ）1 （D ）4X7.7（哈尔滨工业大学2002考研题）下面的几种描述中，正确的为 。

（A ）系统函数能提供求解零输入响应所需的全部信息；（B ）系统函数的零点位置影响时域波形的衰减或增长； （C ）若零极点离虚轴很远，则它们对频率响应的影响非常小； （D ）原点的二阶极点对应)(2t t ε形式的滤形。

专业课习题解析课程西安电子科技大学信号与系统第二章2-12-22-42-82-122-16波形图如图2-9(a)所示。

波形图如图2-9(b)所示。

波形图如图2-9(c)所示。

波形图如图2-9(d)所示。

波形图如图2-9(e)所示。

2-202-222-282-29第三章习题3.1、3.63.8、3.9、3.10、3.11、3.13、求题3.9图所示各系统的阶跃响应。

3.14、求图所示系统的单位序列响应和阶跃响应。

3.15、若LTI离散系统的阶跃响应，求其单位序列响3.16、如图所示系统，试求当激励分别为（1）（2）3.18、3.22、第四章习题4.64.74.104-114.174.184.194.204.214.254.234.274.284.294.314.334.34某LTI 系统的频率响应ωωωj j j H +-=22)(，若系统输入)2cos()(t t f =，求该系统的输出)(t y 。

4.35 一理想低通滤波器的频率响应⎪⎩⎪⎨⎧><-=s rad srad j H /3,0/3,31)(ωωωω4.36 一个LTI 系统的频率响应4.394.45 如图4-42(a)的系统，带通滤波器的频率响应如图(b)所示，其相频特性0)(=ωϕ，若输入图4-424.484.50图4-47图4-48图4-49 4.53 求下列离散周期信号的傅里叶系数。

第五章5-2 求图5-1所示各信号拉普拉斯变换，并注明收敛域。

5-35-45-65-75-85-9其波形如下图所示：其波形如下图所示：其波形如下图所示：5-105-125-135-15。

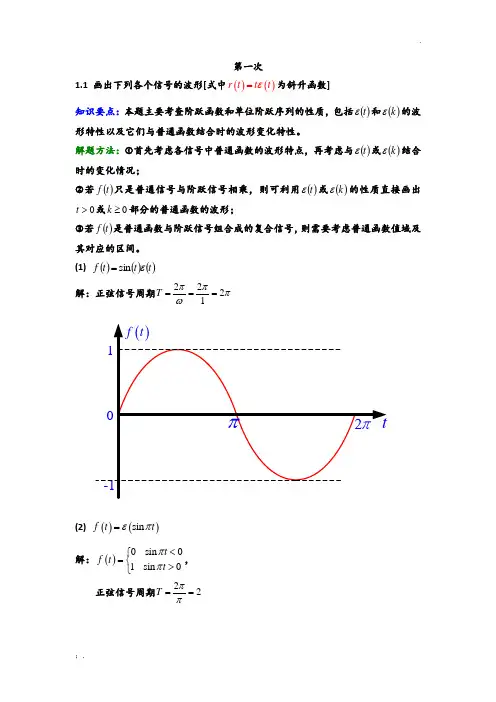
第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。

解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。

(1) ()()()t t t f εsin = 解：正弦信号周期ππωπ2122===T(2) ()()sin f t t επ=解：()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩，正弦信号周期22==ππT(3) ()()cos f t r t =解：()0 cost 0cos cos 0f t t t <⎧=⎨>⎩，正弦信号周期221T ππ==(4) ()()k k k f ε)12(+=(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦1.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。

解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。

(1) ()()()()315122f t t t t εεε=+--+-(2) ()()()12f t r t t ε=--tt)1t-t (3)()()()()sin13f t t t tπεε=---⎡⎤⎣⎦解：22Tππ==(4) ()()()()25f k k k k εε=+--⎡⎤⎣⎦(5) ()()()241k f k k k εε=---⎡⎤⎣⎦1.3 写出下图所示各波形的表达式 (1)解：()()()()()()()()()()()2111223 211223f t t t t t t t t t t t εεεεεεεεεε=+--+-------⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=+----+-(2)解：24T πω==2πω∴=⇒10cos 2t π⎛⎫⎪⎝⎭()()()10cos 112f t t t t πεε⎛⎫=+--⎡⎤ ⎪⎣⎦⎝⎭1.4 写出下图所示各序列的闭合形式的表示式 (a)解：()()3f k k ε=+ (b)解：()()()38f k k k εε=---(课堂已讲)1.5 判别下列各序列是否为周期性的，如果是，确定其周期(1) ()2cos 5f k k π⎛⎫=⎪⎝⎭解：25πβ=25252ππβπ=⨯= 5N ∴= 周期序列(2) ()⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+=632cos 443sin ππππk k k f 解：431πβ=，3834221=⨯=ππβπ，∴m 取3，81=∴N ； 322πβ=，323222=⨯=ππβπ，32=∴N ； 故24=N(3) ()⎪⎭⎫⎝⎛+=k k k f 2sin 2cos 3π解：11=β，ππβπ21221=⨯=，故非周期；22πβ=，42222=⨯=ππβπ，42=∴N ；故非周期1.6 已知信号的波形如下图所示，画出下列各函数的波形(1) ()()t t f --22ε)(2) ()12f t -(3)() dd f tt1.7 已知序列的图形如图所示，画出下列各序列的图形(1) ()()()24f k k k εε---⎡⎤⎣⎦(2) ()()21f k k ε-+-+1.8 信号()t f 22-的波形图如下所示，试画出()t f 和()ττd ⎰∞-tf 的波形解：由图可知：()()()()222+---=t t t t f δεε，则 当0<t 时，()()()22d 2)2(d +-=+-=⎰⎰∞-∞-t t f ttετδττ；当20≤≤t 时，()()()()()2d 22d 1 d ]222[d -=+-⋅=+---=⎰⎰⎰⎰∞-∞-∞-∞-t t t t f tttt ττδττδεεττ当2>t 时，()()()()022 2d 1 2d 1 d ]222[d 2=-=-⋅=-⋅=+---=⎰⎰⎰⎰∞-∞-∞-ττττδτετεττt ttf(课堂已讲)1.9 已知信号的波形如图所示，分别画出()f t 和()d d f t t的波形解：第二次1.10 计算下列各题()001t at t t a a δδ⎛⎫-=- ⎪⎝⎭，()()0001t t f t at t f t a a a δδ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭(1)()()01sin d 2t t t t πδδ-∞⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎰ 解：()()()()()()00001sin d 21 sin d sin d 2 sin 0t f t t t t tt t t t t t t πδδπδπδπ---∞∞∞=⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=++ ⎪⎝⎭==⎰⎰⎰(2)()()2[2]d t e t t t δδ∞--∞'+⎰解：()()()()()()()()()()()22220[2]d [2]d [22]d [22]d 044t t t tt f t e t t te t e t tt e t t t t t t t δδδδδδδδδδ∞--∞+∞---∞+∞-=-∞+∞-∞'=+'=+'=++'=++=+=⎰⎰⎰⎰(3)()2sin 3d 4t t t t πδ∞-∞⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎰ 解：()()2232 sin 3d 4sin 433sin 439sin492t t t t t t t πδπππ∞-∞=-⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=+ ⎪⎝⎭⎛⎫=-+- ⎪⎝⎭=-=-⎰(4)()()2d tx x x δ-∞'-⎰解：()()()()()()()() 2d 2d 2d d 2ttttx x xx x x x x x xt t δδδδδδε-∞-∞-∞-∞'-'=+⎡⎤⎣⎦'=+=+⎰⎰⎰⎰(5)()()()6236224d t t t t δδ--++⎡⎤⎣⎦⎰ 解：()()()()()()()()()()()()6236622336223623226224d 6d 2624d 16262d 2662d 66628t t t t t tt t t t t tt t t tt t tt δδδδδδ---=--=--++⎡⎤⎣⎦=-+-+=-+-⋅+=+-+=+-=+=⎰⎰⎰⎰⎰(6)()2(2)2d tτδττ+-⎰解：()()()20202022(2)2d (2)[(2)]d (2)2d 2| ,2 (42)(2) 6(2)tttt f t t t t t τδτττδτττδττεε==+-=+--=+-=+≥=+-=-⎰⎰⎰(7)()()55342d t t t δ---⎰解：()()()()()()()()()555555552 342d 324d 132d 2132d 213212t t t t t t tt t t t t t t δδδδ----=--=--=-⋅-=--=-=-⎰⎰⎰⎰ (8)()02d 3tτδττ-⎛⎫- ⎪⎝⎭⎰解：()()()()()()()00002d 332d 32d 32,06t ttt t ττδττδττττδτττε---=⎛⎫- ⎪⎝⎭=-=-=-≥=-⎰⎰⎰(课堂已讲)1.11 设系统的初始状态为()0x ，激励为()f ⋅，各系统的全响应()y ⋅与激励和初始状态的关系如下，试分析各系统是否是线性的。

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统（一）专业课习题解析课程第2讲第一章信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

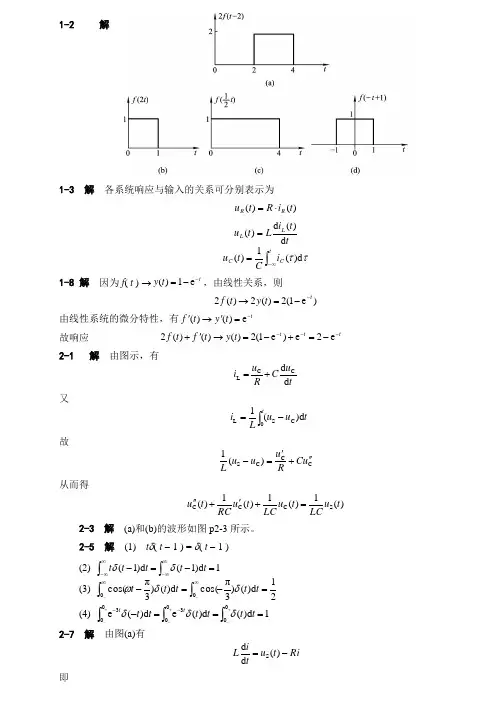
专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第2讲第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f =（7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+= 解：各信号波形为（2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)tf=r)(sin(t（7）)f kε=t)(2(k（10）)(])1(1[)(k k f kε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

专业课习题解析课程西安电子科技大学844信号与系统精选专业课习题解析课程第2讲第一章信号与系统（二）精选精选1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fε=t)(sin(t（5）)tf=r(t)(sin精选（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1()1[精选精选1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε精选精选（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε精选1-3 写出图1-3所示各波形的表达式。

精选1-4 写出图1-4所示各序列的闭合形式表达式。