西南交大考研试题(信号与系统)
- 格式:doc
- 大小:814.50 KB
- 文档页数:19

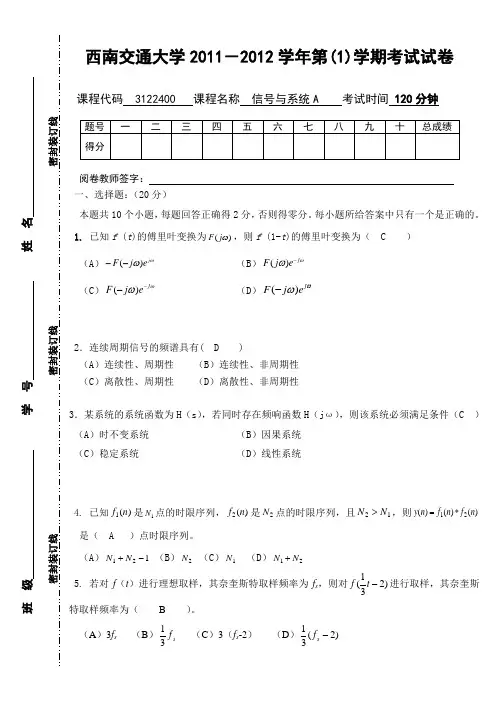
西南交通大学2011-2012学年第(1)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1. 已知f (t )的傅里叶变换为)(ωj F ,则f (1-t )的傅里叶变换为( C ) (A )ωωj e j F )(-- (B )ωωj ej F -)((C )ωωj e j F --)((D )ωωj ej F )(-2.连续周期信号的频谱具有( D )(A )连续性、周期性 (B )连续性、非周期性 (C )离散性、周期性 (D )离散性、非周期性3.某系统的系统函数为H (s ),若同时存在频响函数H (j ω),则该系统必须满足条件(C ) (A )时不变系统 (B )因果系统 (C )稳定系统 (D )线性系统4. 已知)(1n f 是1N 点的时限序列,)(2n f 是2N 点的时限序列,且12N N >,则)()()(21n f n f n y *= 是( A )点时限序列。
(A )121-+N N (B )2N (C )1N (D )21N N +5. 若对f (t )进行理想取样,其奈奎斯特取样频率为f s ,则对)231(-t f 进行取样,其奈奎斯特取样频率为( B )。
(A )3f s (B )s f 31 (C )3(f s -2) (D ))2(31-s f 班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6. 周期信号f(t)如题图所示,其直流分量等于( B )(A )0 (B )4 (C )2(D )67. 理想不失真传输系统的传输函数H (jω)是 ( B )。
(A )0j tKe ω- (B )0t j Ke ω-(C )0t j Ke ω-[]()()c c u u ωωωω+--(D )00j t Keω- (00,,,c t k ωω为常数)8.已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为( A )。



2000年一、选择题(每小题3分,共30分)1、已知y (t )=x (t )*h (t ),g (t )=x (3t )*h (3t ),x (t )?X (j ?),h (t )?H (j ?),则g (t ) = ( )。
(a )⎪⎭⎫ ⎝⎛33t y(b )⎪⎭⎫ ⎝⎛331t y (c )()t y 331(d )()t y 3912、差分方程)()2()5()3(6)(k f k f k y k y k y --=+++-所描述的系统是( )的线性时不变系统。
(a )五阶 (b )六阶 (c )三阶 (d )八阶3、已知信号f 1(t ),f 2(t )的频带宽度分别为??1和??2,且??2>??1,则信号y (t )= f 1(t )*f 2(t )的不失真采样间隔(奈奎斯特间隔)T 等于( )。
(a )21πωω∆+∆(b )12πωω∆-∆(c )2πω∆ (d )1πω∆ 4、已知f (t )?F (j ?),则信号y (t )= f (t )? (t -2)的频谱函数Y (j ?)=( )。
(a )ωω2j e)j (F(b )ω2-j e)2(f(c ))2(f (d )ω2j e)2(f5、已知一线性时不变系统的系统函数为)2)(1(1-)(-+=s s s s H ,若系统是因果的,则系统函数H (s )的收敛域ROC 应为( )。
(a )2]Re[>s(b )1]Re[-<s(c )2]Re[<s (d )2]Re[1<<-s6、某线性时不变系统的频率特性为ωωωj j )j (-+=a a H ,其中a >0,则此系统的幅频特性|H (j ?)|=( )。
(a )21 (b )1(c )⎪⎭⎫⎝⎛-a ω1tan (d )⎪⎭⎫ ⎝⎛-a ω1tan 27、已知输入信号x (n )是N 点有限长序列,线性时不变系统的单位函数响应h (n )是M 点有限长序列,且M >N ,则系统输出信号为y (n )= x (n )*h (n )是( )点有限长序列。



西南交大考研试题(信号与系统)2000年一、选择题(每小题3分,共30分)1、已知y (t )=x (t )*h (t ),g (t )=x (3t )*h (3t ),x (t )X (j ),h (t )H (j ),则g (t ) = ( )。
(a )??33t y(b )331t y (c )()t y 331(d )()t y 3912、差分方程)()2()5()3(6)(k f k f k y k y k y --=+++-所描述的系统是()的线性时不变系统。
(a )五阶(b )六阶(c )三阶(d )八阶 3、已知信号f 1(t ),f 2(t )的频带宽度分别为1和2,且2>1,则信号y (t )= f 1(t )*f 2(t )的不失真采样间隔(奈奎斯特间隔)T 等于()。
(a )21πωω?+?(b )12πωω?-?(c )2πω? (d )1πω? 4、已知f (t )F (j ),则信号y (t )= f (t ) (t -2)的频谱函数Y (j )=()。
(a )ωω2j e)j (F(b )ω2-j e)2(f(c ))2(f (d )ω2j e)2(f5、已知一线性时不变系统的系统函数为)2)(1(1-)(-+=s s s s H ,若系统是因果的,则系统函数H (s )的收敛域ROC 应为()。
(a )2]Re[>s(b )1]Re[-<s< p="">(c )2]Re[6、某线性时不变系统的频率特性为ωωωj j )j (-+=a a H ,其中a >0,则此系统的幅频特性|H (j )|=()。
(a )21(b )1(c )??-a ω1tan (d )??? ??-a ω1tan 27、已知输入信号x (n )是N 点有限长序列,线性时不变系统的单位函数响应h (n )是M 点有限长序列,且M >N ,则系统输出信号为y (n )= x (n )*h (n )是()点有限长序列。
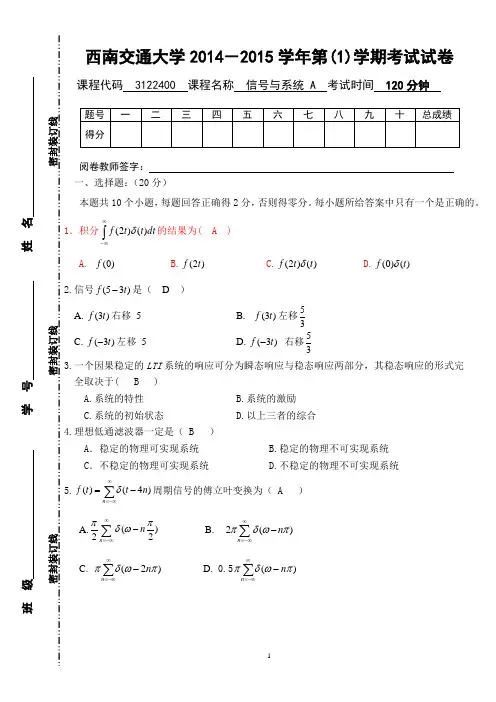
西南交通大学2014-2015学年第(1)学期考试试卷课程代码 3122400 课程名称 信号与系统 A 考试时间 120分钟阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1.积分⎰∞∞-dt t t f )()2(δ的结果为( A )A. )0(fB.)2(t fC.)()2(t t f δD.)()0(t f δ 2.信号)35(t f -是( D ) A .)3(t f 右移 5 B . )3(t f 左移35C .)3(t f -左移 5D .)3(t f - 右移353.一个因果稳定的LTI 系统的响应可分为瞬态响应与稳态响应两部分,其稳态响应的形式完 全取决于( B ) A.系统的特性 B.系统的激励 C.系统的初始状态D.以上三者的综合4.理想低通滤波器一定是( B )A .稳定的物理可实现系统 B.稳定的物理不可实现系统 C .不稳定的物理可实现系统 D.不稳定的物理不可实现系统 5.∑∞-∞=-=n n t t f )4()(δ周期信号的傅立叶变换为( A )A.∑∞-∞=-n n )2(2πωδπB. 2()n n πδωπ∞=-∞-∑C. ∑∞-∞=-n n )2(πωδπ D. 0.5∑∞-∞=-n n )(πωδπ班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6.已知Z 变换Z 1311)]([--=z n x ,收敛域3>z ,则逆变换x (n )为(A )A .)(3n u n B. )(3n u n -- C.)(3n u n -- D.)1(3---n u n7.假设信号)(1t f 的奈奎斯特取样频率为1ω ,)(2t f 的奈奎斯特取样频率为,2ω且1ω>,2ω则信号)2()1()(21+*+=t f t f t f 的奈奎斯特取样频率为( B )(A )1ω (B )2ω (C )1ω+2ω (D )1ω*2ω 8.连续时间信号)(t f 的拉氏变换的收敛域是( A )A .带状 B.环状 C.与σ无关 D.与ω变量有关9.单边拉氏变换2)()2(+=+-s e s F s 的原函数=)(t f ( C )A .)1(e )1(2---t u t B. )2(e )2(2---t u t C .)1(e 2--t u t D. )2(e 2--t u t 10.系统的零点都在左半平面,则该系统一定是( D )A .全通网络 B.低通滤波网络 C.非最小相移网络 D.最小相移网络二、(10分)已知)5(t f -的波形如图所示,试画出)42(+t f 的波形。
2000年一、选择题(每小题3分,共30分)1、已知y (t )=x (t )*h (t ),g (t )=x (3t )*h (3t ),x (t )↔X (j ω),h (t )↔H (j ω),则g (t ) = ( )。
(a )⎪⎭⎫ ⎝⎛33t y(b )⎪⎭⎫ ⎝⎛331t y (c )()t y 331(d )()t y 3912、差分方程)()2()5()3(6)(k f k f k y k y k y --=+++-所描述的系统是( )的线性时不变系统。
(a )五阶 (b )六阶 (c )三阶 (d )八阶3、已知信号f 1(t ),f 2(t )的频带宽度分别为∆ω1和∆ω2,且∆ω2>∆ω1,则信号y (t )= f 1(t )*f 2(t )的不失真采样间隔(奈奎斯特间隔)T 等于( )。
(a )21πωω∆+∆(b )12πωω∆-∆(c )2πω∆ (d )1πω∆ 4、已知f (t )↔F (j ω),则信号y (t )= f (t )δ (t -2)的频谱函数Y (j ω)=( )。
(a )ωω2j e)j (F(b )ω2-j e)2(f(c ))2(f (d )ω2j e)2(f5、已知一线性时不变系统的系统函数为)2)(1(1-)(-+=s s s s H ,若系统是因果的,则系统函数H (s )的收敛域ROC 应为( )。
(a )2]Re[>s(b )1]Re[-<s(c )2]Re[<s (d )2]Re[1<<-s6、某线性时不变系统的频率特性为ωωωj j )j (-+=a a H ,其中a >0,则此系统的幅频特性|H (j ω)|=( )。
(a )21(b )1(c )⎪⎭⎫⎝⎛-a ω1tan (d )⎪⎭⎫ ⎝⎛-a ω1tan 2 7、已知输入信号x (n )是N 点有限长序列,线性时不变系统的单位函数响应h (n )是M 点有限长序列,且M >N ,则系统输出信号为y (n )= x (n )*h (n )是( )点有限长序列。
(a )N +M (b )N +M -1 (c )M (d )N 8、有一信号y (n )的Z 变换的表达式为1131124111)(---+-=z z z Y ,如果其Z 变换的收敛域为31||41<<z ,则Y (z )的反变换为y (n )等于( )。
(a ))(312)(41n u n u nn ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛(b ))1(312)(41--⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛n u n u nn(c ))1(312)(41--⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛n u n u nn(d ))1(312)1(41--⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-n u n u nn9、x (t ), y (t )分别是系统的输入和输出,则下面的4个方程中,只有( )才描述的因果线性、时不变的连续系统。
(a ))1()(+=t x t y(b )0)()()(=+'t x t y t y(c ))()()(t x t ty t y =+'(d ))()()(2)(t x t y t y t y '=+'+''10、双向序列f (k ) = a | k | 存在Z 变换的条件是( )。
(a )a >1 (b )a <1 (c )a ≥1 (d )a ≤1二、(15分) 如下图所示系统,已知输入信号的频谱X (j ω)如图所示,试确定并粗略画出y (t )的频谱Y (j ω)。
三、(10分)已知系统函数)3)(1(1)(++=s s s H 。
激励信号)(e )(2t u t f t-=。
求系统的零状态响应y f (t )。
四、(10分)如下图所示系统,已知11)(+=s s G 。
求:(1)系统的系统函数H (s ); (2)在s 平面画出零极点图; (3)判定系统的稳定性; (4)求系统的的冲激响应。
五、(15分)求一个理想低通滤波器对具有sinc 函数x (t )的响应问题,即x0-20 F (s )(s )ttt x πsin )(i ω=当然,该理想低通滤波器的冲激响应具有与x (t )相类似的形式,即ttt h πsin )(c ω=试证明该滤波器的输出y (t )还是一个sinc 函数。
(注:sinc(x )=sin πx /πx ) 六、(20分)有一个离散因果线性时不变系统,其差分方程为)()1()(310)1(n x n y n y n y =++-- (1) 求该系统的系统函数H (z ),并画出零极点图,指出收敛域; (2) 求系统的单位函数响应;(3) 你应能发现该系统是不稳定的,求一个满足该差分方程的稳定(非因果)单位函数响应。
2001年一、选择题(15分)1、差分方程3y (k )-4y (k -3)+8y (k -5)=2f (k -2)所描述的系统是( )线性时不变系统。
(A )五阶 (B)六阶 (C )一阶 (D )四阶2、一连续信号x (t )从一个截止频率为ωc =1000π的理想低通滤波器输出得到,如果对x (t )完成冲激抽样,下列采样周期中的哪一个可能保证x (t )在利用一个合适的低通滤波器后能从它的样本中得到恢复?( )(A )T =10-4s (B)T =10-2s (C )T =5⨯10-2s (D )T =2⨯10-3s3、试确定如下离散时间信号n n n x 43πj32πj ee)(+=的基波周期。
( )(A )12 (B)24 (C )12π (D )24π4、信号e j2t δ '(t )的傅里叶变换为( )。
(A )-2 (B)j(ω-2) (C )j(ω+2) (D )2+ j ω5、考虑一连续时间系统,其输入x (t )和输出y (t )的关系为y (t ) = t x (t ),系统是( )。
(A )线性时变系统 (B)线性时不变系统 (C )非线性时变系统 (D )非线性时不变系统 二、(10分)有一因果线性时不变系统,其频率响应为31)(+=s s H ,对于特定的x (t ),观察到系统的输出为)(e )(e)(43t u t u t y t t---=,求x (t )。
三、(10分)考虑一连续时间因果稳定的线性时不变系统,其输入x (t )和输出y (t )的微分方程为)(2)(5d )(d t x t y tt y =+ 问:该系统阶跃响应s (t )的终值s (∞)是多少? 四、(15分)画图题(1)(5分)信号如图所示,试画出⎪⎭⎫ ⎝⎛+123t x 的波形。
(2)(10分)已知)(t x '如图所示,求x (t )。
五、(10分)有一连续时间最小相位系统S ,其频率响应H (j ω)的波特图如图所示,试写出H (j ω)的表达式。
x ' (t )t 0 2 4 2 1 -3六、(20分)某离散线性时不变系统由下面的差分方程描述)1()2(23)1(27)(-=-+--n x n y n y n y (1)求该系统的系统函数H (z ),并画出零极点分布图;(2)限定系统是因果的,写出H (z )的收敛域,并求出单位函数响应h (n ),系统是否稳定? (3)确定使系统稳定的收敛域,并求出h (n )。
七、(20分)带限信号f (t )的频谱密度F (j ω)如图a 所示。
系统(图b )中两个理想滤波器的截止频率均为ωc ,相移为零。
当f (t )通过图b 所示系统时,请画出:A 、B 、C 、D 各点信号的频谱图。
cc1H 2(j ω) c cos(c +1) t 图a图b2002年一、选择题(15分)1、下列系统函数中,( )是最小相位系统。
(A ))5)(4)(3()2)(1()(+++++=s s s s s s H(B ))5)(4)(3()2)(1()(++++-=s s s s s s H(C ))5)(4)(3()2)(1()(++-++=s s s s s s H(D ))5)(4)(3()2)(1()(+++--=s s s s s s H2、有一信号y (n )的Z 变换的表达式为11512311)(---+-=zz z Y ,如果其Z 变换的收敛域为3<|z |<5,则Y (z )的反变换y (n )等于( )。
(A ))()5(2)(3n u n u nn+(B ))1()5(2)(3--+n u n u nn (C ))1()5(2)(3---n u n u nn(D ))1()5(2)1(3------n u n u nn3、试确定离散时间信号)14sin()110cos(2)(--+=t t n x 的基波周期。
( ) (A )5π(B )π(C )2π (D )104、若信号f (t ) = u (t )-u (t -1),则其傅里叶变换F (ω) = ( )。
(A )2je2sin1ωωω-(B ))e -1(j 2j ωω-(C ))e -1(j j ωω(D )2j e 2sin 2ωωω- 5、下列系统( )是因果、线性、时不变的系统。
(A ))()1()(n nx n y n y =++ (B ))2()()()1(+=-+n nx n y n x n y (C ))()1()(n x n y n y =--(D ))2()1()(+=+-n x n y n y二、(20分)画图题已知信号x (t )的傅里叶变换)]2()2([2)(--+=ωωωu u X 如图1所示,其相位频谱0)(=ωϕ。
(1)画出)2()(t x t y =的幅度频谱和相位频谱。
(2)画出)2()(-=t x t y 的幅度频谱和相位频谱。
(3)画出)()(t x t y '=的幅度频谱和相位频谱。
(4)画出)()(2t x t y =的幅度频谱和相位频谱。
三、(20分)有一因果LTI 系统,其方框图如图所示。
试求:(1)画出系统的信号流图。
(2)确定系统函数H (s ),画出零极点分布图,判断系统是否稳定。
(3)确定描述该系统输入x (t )到输出y (t )的微分方程。
(4)当输入x (t )=e -3t u (t ),求系统的零状态响应y (t ),并判断其中的自由响应分量、受迫响应分量、稳-态响应分量、暂态响应分量。
四、(15分)设f (t )为频带有限信号,频带宽度为ωm =8,其频谱F (ω)如下图所示。
(1)求f (t )的奈奎斯特抽样频率ωs 和f s 、奈奎斯特间隔T s 。