周期法求自功率谱密度

三、功率谱分析字体[大] [中] [小]周期信号的功率谱为其双边幅值频谱的平方|c n|2;非周期信号的功率谱为其幅值谱密度的平方|X(ω)|2＝X(ω)X*(ω)。

随机信号属于时域无限信号，其频率、幅值和相位为随机变量。

因而，采用具有统计特性的功率谱估计进行谱分析(一)自功率谱密度及其估计各态历经随机信号的功率谱密度S x(ω)与自相关函数R x(τ)为傅里叶变换偶对，即为了方便，也可用在非负频率范围内(ω>0)定义的单边功率谱密度G x(ω)代替双边功率谱密度S x(ω)，两者之间的关系为自功率谱估计可分为线性估计法与非线性估计法。

前者以快速变换为基础，应用较早，也称为经典谱分析法; 后者是与时序模型结合的一种新方法，又称为现代谱分析方法。

1. 周期图各态历经随机信号的均方值ψx2为信号能量的时域描述。

巴什瓦定理表明，信号能量的时域计算与频域计算相等，即由此定义自功率谱密度及其估计为：式中表12-45 典型信号的自相关、频谱、概率密度(续)X(ω)为测试数据x(t)的傅里叶变换，X(k)为N个数据x(n)的离散傅里叶变换，由FFT直接求出。

由于X(k)具有周期函数的性质，所以称由此获得的自功率谱估计为周期图。

自相关估计x′(r)的快速傅里叶变换可作为自功率谱估计的另一计算公式以上两种估计都是自功率谱S x(ω)的有偏估计，只是偏差大小不同。

两种估计在时域对数据或对自相关估计进行截断，相当于加窗处理，致使谱估计成为真实功率谱(或称为真功率谱)与窗谱W(ω)的卷积，即Ŝx(ω)=S x(ω)*W(ω)窗谱旁瓣的泄漏效应和卷积的作用使真功率谱的尖峰数值变化，邻近点的数值变大，造成谱估计的模糊与失真以上两种估计的方差较大; 相距2π/N的各点估计值互不相关，故数据点数N越大，这些点的估计值的随机起伏越严重。

为改善谱估计的估计质量，在增大数据点数的同时，采用平均化处理和窗处理方法减小谱估计的方差。

自功率谱密度频谱
自功率谱密度和频谱是信号处理中常用的概念，它们都与信号的频率内容有关，但具有不同的特性和应用。

1.自功率谱密度（Auto-Power Spectral Density, PSD）：自功率谱密度是信号自相关函数的傅里叶变换。

它描述了信号在不同频率上的功率分布，单位为W/Hz。

自功率谱密度是频率的函数，通常用于分析随机信号或周期性信号的频率特性。

在实际应用中，可以通过计算信号的快速傅里叶变换（FFT）并取其模的平方来近似得到自功率谱密度。

需要注意的是，为了得到准确的功率谱密度，还需要进行适当的窗函数处理和平均处理。

2.频谱（Spectrum）：频谱是信号在频率域上的表示，它描述了信号在不同频率上的幅度和相位。

频谱可以通过对信号进行傅里叶变换得到，结果是一个复数函数，其中实部表示幅度，虚部表示相位。

与自功率谱密度不同，频谱既包含了幅度信息，也包含了相位信息。

在实际应用中，频谱分析被广泛应用于各种领域，如通信、音频处理、图像处理等。

总结来说，自功率谱密度和频谱都是用于描述信号频率特性的工具，但它们的侧重点和应用背景有所不同。

自功率谱密度主要关注信号在不同频率上的功率分布，适用于随机信号或周期性信号的分析；而频谱则提供了更全面的频率域信息，包括幅度和相位，适用于各种信号的处理和分析。

三、功率谱分析字体[大][中][小]周期信号的功率谱为其双边幅值频谱的平方|c n|2;非周期信号的功率谱为其幅值谱密度的平方|X(ω)|2＝X(ω)X*(ω)。

随机信号属于时域无限信号，其频率、幅值和相位为随机变量。

因而，采用具有统计特性的功率谱估计进行谱分析(一)自功率谱密度及其估计各态历经随机信号的功率谱密度S x(ω)与自相关函数R x(τ)为傅里叶变换偶对，即为了方便，也可用在非负频率范围内(ω>0)定义的单边功率谱密度G x(ω)代替双边功率谱密度S x(ω)，两者之间的关系为自功率谱估计可分为线性估计法与非线性估计法。

前者以快速变换为基础，应用较早，也称为经典谱分析法; 后者是与时序模型结合的一种新方法，又称为现代谱分析方法。

1. 周期图各态历经随机信号的均方值ψx2为信号能量的时域描述。

巴什瓦定理表明，信号能量的时域计算与频域计算相等，即由此定义自功率谱密度及其估计为：式中表12-45 典型信号的自相关、频谱、概率密度(续)X(ω)为测试数据x(t)的傅里叶变换，X(k)为N个数据x(n)的离散傅里叶变换，由FFT 直接求出。

由于X(k)具有周期函数的性质，所以称由此获得的自功率谱估计为周期图。

自相关估计x′(r)的快速傅里叶变换可作为自功率谱估计的另一计算公式以上两种估计都是自功率谱S x(ω)的有偏估计，只是偏差大小不同。

两种估计在时域对数据或对自相关估计进行截断，相当于加窗处理，致使谱估计成为真实功率谱(或称为真功率谱)与窗谱W(ω)的卷积，即Ŝx(ω)=S x(ω)*W(ω)窗谱旁瓣的泄漏效应和卷积的作用使真功率谱的尖峰数值变化，邻近点的数值变大，造成谱估计的模糊与失真以上两种估计的方差较大; 相距2π/N的各点估计值互不相关，故数据点数N越大，这些点的估计值的随机起伏越严重。

为改善谱估计的估计质量，在增大数据点数的同时，采用平均化处理和窗处理方法减小谱估计的方差。

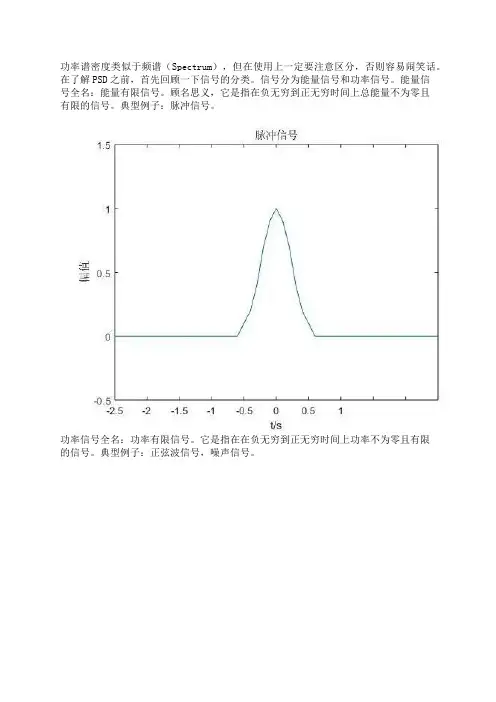
功率谱密度类似于频谱（Spectrum），但在使用上一定要注意区分，否则容易闹笑话。

在了解PSD之前，首先回顾一下信号的分类。

信号分为能量信号和功率信号。

能量信号全名：能量有限信号。

顾名思义，它是指在负无穷到正无穷时间上总能量不为零且有限的信号。

典型例子：脉冲信号。

功率信号全名：功率有限信号。

它是指在在负无穷到正无穷时间上功率不为零且有限的信号。

典型例子：正弦波信号，噪声信号。

一个信号不可能既是能量信号又是功率信号。

能量信号在无穷大时间上功率为0，不满足功率信号功率不为0的定义；而功率信号在无穷大时间上能量为无穷大，不满足能量有限的定义。

一个信号可以既不是能量信号也不是功率信号，如下面这个信号，其功率无限能量也无限。

能量信号和功率信号的范围不包括所有的信号类型，这是因为工程上一般就是这两种，足以满足描述的需要了。

功率信号还可以细分为周期信号（如正弦波信号）和随机信号（如噪声信号）。

随机信号的定义：幅度未可预知但又服从一定统计特性的信号，又称不确定信号。

综上，上文提到的信号分类如下图所示：对能量信号和周期信号，其傅里叶变换收敛，因此可以用频谱（Spectrum）来描述；对于随机信号（实际的信号基本上是随机信号），傅里叶变换不收敛，因此不能用频谱来描述，而应当使用功率谱密度（PSD）。

能量信号和周期信号通常在教学仿真中用得比较多，而工程上的信号通常都是随机信号，即使原始信号是周期信号，由于数据采集过程中存在噪声，实际获得的信号仍然会是随机信号。

如果在工程应用上用“频谱”而不是“功率谱密度”来表述，会稍显不专业，但是我感觉好像很多工程人员会把这两者混淆起来……在实际应用中，一个信号我们不可能获得无穷长时间段内的点，对于数字信号，只能通过采样的方式获得N个离散的点。

上文提到，实际信号基本上是随机信号，由于不可能对所有点进行考察，我们也就不可能获得其精确的功率谱密度，而只能利用谱估计的方法来“估计”功率谱密度。

功率谱估计的方法
功率谱估计是信号处理中常用的一种方法，用于分析信号在频域内的特点，通常可以分为以下几种方法：
一、经典方法
1.傅里叶变换法：将时域信号通过傅里叶变换变换到频域，然后计算功率谱密度。

2.自相关法：通过自相关函数反映信号的统计平稳性，然后通过傅里叶变换计算功率谱密度。

3.周期图法：将信号分解为若干个周期波形，然后对每个周期波形进行傅里叶变换计算周期功率谱，最后汇总得到整个信号的功率谱。

二、非经典方法
1. 时-频分析法：如短时傅里叶变换（STFT）、小波变换等，将信号分解为时域和频域两个维度的分量，从而可以分析信号在时间和频率上的变化。

2. 基于协方差矩阵的特征值分解法：通过建立协方差矩阵，在张成空
间中求解特征向量，从而达到计算信号功率谱的目的。

3. 基于频率锁定法：如MUSIC法、ESPRIT法等，是一种利用特定信号空间中的特定模式进行处理的方法。

以上方法各有特点，根据实际需求选择不同的方法可以得到相应的功率谱估计结果。

功率谱密度（Power Spectral Density，简称PSD）是描述信号或时间序列的频率内容的一种方式。

在物理学、工程学以及数据分析等领域中，功率谱密度是一种常用的分析工具。

PSD表示了信号在各个频率上的功率分布，它描述了信号功率随频率的变化情况。

功率谱密度可以视为信号频谱的模平方，即对每个频率分量上的幅度进行平方操作。

这种表示方式可以揭示信号中的周期性成分、随机成分以及它们的相对强度。

在信号处理中，功率谱密度常用于分析信号的频率特性和噪声特性。

例如，在通信系统中，通过分析接收信号的功率谱密度，可以判断信道中的噪声类型和信号质量。

在振动分析中，功率谱密度可以帮助识别结构中的共振频率和振动模式。

计算功率谱密度的方法有多种，包括自相关函数法、周期图法、Welch法等。

这些方法各有优缺点，适用于不同类型的信号和分析需求。

在实际应用中，需要根据具体情况选择合适的方法来计算功率谱密度。

随机信号功率谱估计1.随机信号功率谱密度定义定义随机信号信号的功率谱()jw x e P 为： ()()m j xe m r P ωω-+∞-∞=∑=m j x e其中()m r x 为随机信号的自相关函数。

功率谱反映了信号的功率在频域随频率ω分布，因此()jw x e P 又称为功率谱密度。

2. 经典谱估计（非参数谱估计）方法简介经典谱估计的方法主要包括两种方法：BT 法和周期图法。

(1) BT 法（间接法）此方法的理论基础是维纳-辛钦定理。

1958年Blackman 和Tukey 给出了这一种方法的具体实现，即由()n N x 估计出自相关函数()m rˆ，然后对()m r ˆ求傅里叶变换得到()n N x 的功率谱，记之为()ωBTP ˆ，并以此作为对()ωP 的估计，即 ()()m j m e m r ˆˆωω--=∑=M MBT P ， 1-≤N M因为这种方法求出的功率谱是通过自相关函数间接得到的，所以称为间接法，又称BT 法或自相关法。

当M 较小时，上式计算量不是很大，因此，该方法是在FFT 问世之前（即周期图法被广泛应用之前）常用的谱估计方法。

(2) 周期图法（直接法）周期图法又称为直接法，它是把随机信号()n x 的N 点观察数据()n N x 视为一个能量有限信号，直接取()n N x 的傅里叶变换，得()jw e x N ，然后再取其幅值的平方，并除于N ，作为对()n x 真实功率谱()jwe p 的估计。

以()ωPERP ˆ表示用周期图法估计的功率谱，则 ()()21ˆωωN PER X NP =3. 信号参数设定模拟信号：()()()()t w t *110cos 5.1t *100cos 2t x ++=ππ其中()t w 为均值为0，方差为1的白噪声。

采样频率：z 1000f s Hnfft=1024时间长度分别取1s ，10s ，100s4. 仿真结果原始信号波形:BT 法：（1）t=1s （2）t=10s （3）t=100s周期法：（1）t=1s （2）t=10s （3）t=100s由图可以看出，在频率50hz和55hz附近处功率谱有两个峰值，说明信号中有50hz和55hz 的周期成分。

周期图法：周期图法是直接将信号的采样数据x(n)进行傅立叶变换来求取功率谱密度估计。

假设有限长随机信号序列x(n),它的傅立叶变换和功率谱密度估计S存在下列关系：式中，N为随机信号x(n)的长度，在离散的频率点处可得：由于DFT[x(n)]的周期为N，求得的功率谱估计也是以N为周期，故成为周期图法。

AR模型：信号的AR模型定义为：（1）（2）（3）式中x(n)为信号X(k)的下一点的估计，因此，可以用AR模型来进行预报。

式中中P为AR模型阶次，一般可以用模型拟合残差曲线来确定。

当模型阶次增加，残差不在显著下降时，该阶次就是正确的模型阶次。

另外，AR模型是信号的参数化模型，可以从AR模型系数计算出信号的频谱，称为最大墒谱，公式如下：实际工作中，往往只是知道N点数据x(n); 因此，可以按如下步骤估计x(n)的功率谱：（1）、由x(n)估计自相关函数，得r(m);（2）、用r(m)根据Yule-Wslker方程求出AR模型真实参数的估计值，即a(1), a(2), …, ;（3）、将这些参数带入上式（3）中，得到x(n)的功率谱估计程序如下：1，周期图法load y.txt;load x.txt;data=y';M=100;PS=zeros(M,1);vecter=myditfft(data);u=(1/M)*sum(data);for n=1:MPS(n)=(1/M)*(vecter(n)*conj(vecter(n)))+u;endplot(xnian,PS);function y=myditfft(x)%FFT变换，实现DIT-FFT基2算法，%x为给定序列，y为x的离散傅立叶变换%点数取大于等于x的长度的2的幂次m=nextpow2(x);N=2^m;if length(x)<Nx=[x,zeros(1,N-length(x))];endnxd=bin2dec(fliplr(dec2bin([1:N]-1,m)))+1;y=x(nxd);for mm=1:mNmr=2^mm;u=1;WN=exp(-i*2*pi/Nmr);)for j=1:Nmr/2for k=j:Nmr:Nkp=k+Nmr/2;t=y(kp)*u;y(kp)=y(k)-t;y(k)=y(k)+t;endu=u*WN;endend2、AR模型load x,txt;load y.txt;data_burg=y;N=length(y);k=input('k=');A=zeros(N,1);PSD=zeros(1,N);[r,a,sigma]=burg_unknown(data_burg,k);s=sigma(k+1);aa=[1 a(k,[1:k]) zeros(1,N-k-2)];aa_fft=myditfft(aa);for l=1:NA(l)=aa_fft(l)*conj(aa_fft(l));PSD(l)=s/A(l);endplot(xnian,PSD);function [r,a,sigma]=burg_unknown(x,K)N=max(size(x));r=[];ef(1,:)=x;eb(1,:)=x;sigma(1)=sum(x.^2)/N;a=zeros(K+1,K+1);a(:,1)=1;for p=2:K+1;r(p-1)=2*(ef(p-1,[p:N])*eb(p-1,[p-1:N-1])')/(ef(p-1,[p:N])*ef(p-1,[p: N])'+eb(p-1,[p-1:N-1])*eb(p-1,[p-1:N-1])');sigma(p)=(1-r(p-1).^2)*sigma(p-1);for i=2:p-1a(p,i)=a(p-1,i)-r(p-1)*a(p-1,p-i+1);enda(p,p)=-r(p-1);for n=2:Nef(p,n)=ef(p-1,n)-r(p-1)*eb(p-1,n-1);eb(p,n)=-r(p-1)*ef(p-1,n)+eb(p-1,n-1);endenda=a([2:K+1],[2:K+1]);end。

随机信号的功率谱估计方法随机信号的功率谱估计方法介绍随机信号是指信号的每个值都是随机的，即在同一时刻下，其取值可以是不同的。

由于随机性导致了随机信号的分布不确定，因此分析随机信号的机理比较复杂。

一个优秀的信号分析方法是估计随机信号的功率谱。

功率谱是一个很有用的统计量，它描述了信号在不同频率上的能量分布。

估计功率谱可以帮助我们了解信号的构成、将信号分解成不同的频率分量、对信号的特征进行定量分析，以及在通信和控制系统中使用。

本文将介绍几种常见的随机信号功率谱估计方法，包括周期图法、自相关函数法、半岭功率谱估计法和最大熵谱估计法。

方法一、周期图法周期图法经常用于信号频谱估计。

当我们有大量采样数据时，可以通过对信号进行傅里叶变换来计算功率谱。

但是，当信号是随机过程时，它的频谱也是一个随机变量，因此我们必须通过使用大量的测量值来确定频谱估计的不确定性。

由此带来的问题是，我们要计算的是随机过程信号的平均功率谱密度函数，而不仅仅是单次测量结果的功率谱。

周期图法通过将数据分成多个重叠的子段，然后计算每个子段的傅立叶变换来估计平均功率谱密度函数。

二、自相关函数法自相关函数法采用的是自相关函数相关的频谱估计方法。

通过对随机信号进行卷积，可以获得信号的自相关函数。

自相关函数是指信号与自身的延迟信号的乘积。

自相关函数可以通过傅立叶变换来计算功率谱密度函数。

这种方法可以用于非平稳和平稳信号，并且在信号较长的情况下效果良好。

三、半岭功率谱估计法半岭功率谱估计法是利用谱曲线的形状确定能量的集中程度。

半岭是谱曲线上右侧的谷底点。

我们可以将信号的谱曲线绘制出来，并计算它到半岭的近似功率谱曲线。

该方法可以适用于处理非平稳信号，需要进行多次计算才能获得准确结果。

四、最大熵谱估计法最大熵谱估计法可以通过最小化误差来估计功率谱密度函数。

该方法通过将信号视为时间序列，然后利用最大熵原理来进行谱估计。

最大熵原理是指在不知道任何关于信号的先验信息的情况下，使用最少的假设来描述数据的过程。

功率谱估计报告范文
一、功率谱估计的原理
功率谱估计是用来估计信号的功率谱密度（PSD）。

功率谱密度是描述信号在不同频率上的功率分布情况，是信号频谱特征的重要指标之一、功率谱估计的目标是通过有限长的信号序列来估计信号的功率谱密度，从而得到信号的频谱特征。

二、功率谱估计的常用方法
1.周期图法
周期图法是通过信号的周期性来估计功率谱密度。

该方法将有限长的信号序列进行周期延拓，然后通过傅里叶变换或卷积运算得到功率谱密度估计。

2.自相关法
自相关法是通过信号的自相关函数来估计功率谱密度。

该方法先计算信号序列的自相关函数，然后通过傅里叶变换得到功率谱密度估计。

3.平均功率谱法
平均功率谱法是通过将信号序列分段并求取每段的功率谱密度，然后对各段的功率谱密度进行均值运算来估计信号的功率谱密度。

常用的平均功率谱法有Welch法和Bartlett法。

三、功率谱估计的实际应用案例
1.语音信号处理
2.无线通信
3.振动信号分析
总之，功率谱估计是分析信号频谱特征的常用方法，通过对有限长的信号序列进行处理，估计信号的功率谱密度。

功率谱估计可以应用于语音信号处理、无线通信以及振动信号分析等多个领域。

在实际应用中，根据信号特点和需求选择合适的功率谱估计方法，并结合其他信号处理技术进行综合分析。

功率谱估计方法的比较与评价功率谱估计是信号处理领域的重要工具，用于分析信号的频率内容和能量分布。

随着科技的进步，出现了多种功率谱估计方法，例如经典的周期图法、快速傅里叶变换法以及最小二乘法等。

本文将对这些方法进行比较与评价，旨在找出最适合于不同应用场景的功率谱估计方法。

一、周期图法周期图法是一种常用的功率谱估计方法，它利用信号的自相关函数来计算功率谱。

该方法适用于稳态信号，并能够较好地估计信号的频谱特征。

但周期图法在非稳态信号的估计上存在一定的局限性，并且计算复杂度较高，需要较长的计算时间。

二、快速傅里叶变换法快速傅里叶变换（FFT）法是一种高效的功率谱估计方法，通过将信号从时域转换为频域，可以快速计算出信号的功率谱。

FFT法的优点是计算速度快，适用于大数据量的处理。

然而，由于FFT法是基于信号的离散采样点进行计算的，对于非周期信号的估计效果可能不够准确。

三、最小二乘法最小二乘法是一种经典的信号处理方法，可以用于估计信号的功率谱密度函数。

该方法利用样本点间的相关性来估计信号的频谱分布，并通过最小化误差的平方和来求解最优的谱估计。

最小二乘法的优点是估计结果较为准确，对于非稳态信号的估计效果也较好。

然而，最小二乘法在计算复杂度上稍高，并且对于信噪比较低的信号，估计结果可能受到较大影响。

四、窗函数法窗函数法是一种常见的功率谱估计方法，它通过在时域上对信号进行窗函数加权来减小频谱泄露的影响。

窗函数法对于非周期性和非稳态信号的功率谱估计具有一定的优势，可以提供更准确的估计结果。

然而，在窗函数选择上需要权衡分辨率和频谱失真的平衡，不同的窗函数选择会对结果产生一定的影响。

综上所述，不同的功率谱估计方法适用于不同的应用场景。

周期图法适用于稳态信号的估计；快速傅里叶变换法适用于大数据量的处理；最小二乘法适用于需要较高估计准确度的场景；窗函数法适用于非周期性和非稳态信号的估计。

在具体应用中，需要根据信号特性和实际需求选择合适的功率谱估计方法，以获得准确可靠的结果。

功率信号的自相关函数和功率谱密度
功率信号的自相关函数和功率谱密度是信号处理中的重要概念。

自相关函数用于描述信号的相似度，而功率谱密度则用于描述信号的频率成分。

功率信号的自相关函数是指信号与其自身经过一定时间延迟后
的内积，通常用公式表示为：
R_xx(tau) = E[X(t)X(t+tau)]
其中，X(t)表示功率信号，tau表示时间延迟，E表示期望值。

自相关函数的性质包括：对称性、偶函数性、非负性和可积性。

自相关函数的峰值表示信号的主要周期，自相关函数的宽度表示信号的带宽。

功率信号的功率谱密度是指信号在不同频率下的功率分布，通常用公式表示为：
S_xx(F) = |X(F)|^2
其中，X(F)表示功率信号在频率域中的傅里叶变换。

功率谱密度的性质包括：非负性、实数性、对称性和可积性。

功率谱密度的峰值表示信号的中心频率，功率谱密度的宽度表示信号的带宽。

功率信号的自相关函数和功率谱密度在信号处理中经常被用来
分析和处理信号。

例如，自相关函数可以用于信号的匹配滤波和信号的周期性分析，功率谱密度可以用于信号的频谱分析和滤波器的设计。

- 1 -。

matlab求功率谱密度函数功率谱密度函数是一种用来描述信号频域特性的数学工具，通常用于分析信号的能量分布和频谱特征。

在MATLAB中，有多种方法可以计算功率谱密度函数，包括自定义方法和使用内置函数。

自定义方法1.直接计算信号的幅度谱，然后平方得到功率谱密度函数。

首先，使用FFT函数将时域信号转换为频域信号。

然后，计算频域信号的幅度谱，即信号的模。

最后，将幅度谱平方，得到功率谱密度函数。

```matlabFs=1000;%采样频率T=1/Fs;%采样周期L=1000;%信号长度t=(0:L-1)*T;%时间向量x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 信号Y = fft(x); % 频域信号P = abs(Y/L).^2; % 幅度谱平方f=Fs*(0:(L/2))/L;%频率向量plot(f,P(1:L/2+1))title('单边频谱')xlabel('频率 (Hz)')ylabel('功率谱密度')```2. 使用pwelch函数计算信号的功率谱密度函数。

pwelch函数是MATLAB中内置的一种功率谱密度估计方法，基于Welch方法。

它可以计算信号的分段平均功率谱密度函数，提供更准确的结果。

```matlabFs=1000;%采样频率T=1/Fs;%采样周期L=1000;%信号长度t=(0:L-1)*T;%时间向量x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 信号plot(f,P)title('功率谱密度函数')xlabel('频率 (Hz)')ylabel('功率谱密度')```内置函数除了使用自定义方法外，MATLAB还提供了一些内置函数来计算功率谱密度函数。

1. periodogram函数：基于周期图法计算信号的功率谱密度函数。

三、功率谱分析字体[大][中][小]周期信号的功率谱为其双边幅值频谱的平方|c n|2;非周期信号的功率谱为其幅值谱密度的平方|X(ω)|2＝X(ω)X*(ω)。

随机信号属于时域无限信号，其频率、幅值和相位为随机变量。

因而，采用具有统计特性的功率谱估计进行谱分析(一)自功率谱密度及其估计各态历经随机信号的功率谱密度S x(ω)与自相关函数R x(τ)为傅里叶变换偶对，即为了方便，也可用在非负频率范围内(ω>0)定义的单边功率谱密度G x(ω)代替双边功率谱密度S x(ω)，两者之间的关系为自功率谱估计可分为线性估计法与非线性估计法。

前者以快速变换为基础，应用较早，也称为经典谱分析法; 后者是与时序模型结合的一种新方法，又称为现代谱分析方法。

1. 周期图各态历经随机信号的均方值ψx2为信号能量的时域描述。

巴什瓦定理表明，信号能量的时域计算与频域计算相等，即由此定义自功率谱密度及其估计为：式中表12-45 典型信号的自相关、频谱、概率密度(续)X(ω)为测试数据x(t)的傅里叶变换，X(k)为N个数据x(n)的离散傅里叶变换，由FFT 直接求出。

由于X(k)具有周期函数的性质，所以称由此获得的自功率谱估计为周期图。

自相关估计x′(r)的快速傅里叶变换可作为自功率谱估计的另一计算公式以上两种估计都是自功率谱S x(ω)的有偏估计，只是偏差大小不同。

两种估计在时域对数据或对自相关估计进行截断，相当于加窗处理，致使谱估计成为真实功率谱(或称为真功率谱)与窗谱W(ω)的卷积，即Ŝx(ω)=S x(ω)*W(ω)窗谱旁瓣的泄漏效应和卷积的作用使真功率谱的尖峰数值变化，邻近点的数值变大，造成谱估计的模糊与失真以上两种估计的方差较大; 相距2π/N的各点估计值互不相关，故数据点数N越大，这些点的估计值的随机起伏越严重。

为改善谱估计的估计质量，在增大数据点数的同时，采用平均化处理和窗处理方法减小谱估计的方差。