下载文档原格式
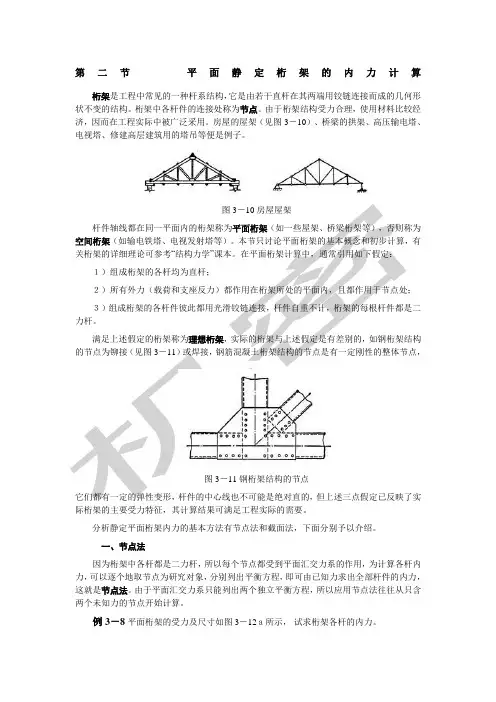
第二节平面静定桁架的内力计算桁架是工程中常见的一种杆系结构，它是由若干直杆在其两端用铰链连接而成的几何形状不变的结构。
桁架中各杆件的连接处称为节点。
由于桁架结构受力合理，使用材料比较经济，因而在工程实际中被广泛采用。
房屋的屋架（见图3－10）、桥梁的拱架、高压输电塔、电视塔、修建高层建筑用的塔吊等便是例子。
图3－10房屋屋架杆件轴线都在同一平面内的桁架称为平面桁架（如一些屋架、桥梁桁架等），否则称为空间桁架（如输电铁塔、电视发射塔等）。
本节只讨论平面桁架的基本概念和初步计算，有关桁架的详细理论可参考“结构力学”课本。
在平面桁架计算中，通常引用如下假定：１）组成桁架的各杆均为直杆；２）所有外力（载荷和支座反力）都作用在桁架所处的平面内，且都作用于节点处；３）组成桁架的各杆件彼此都用光滑铰链连接，杆件自重不计，桁架的每根杆件都是二力杆。
满足上述假定的桁架称为理想桁架，实际的桁架与上述假定是有差别的，如钢桁架结构的节点为铆接（见图3－11）或焊接，钢筋混凝土桁架结构的节点是有一定刚性的整体节点，图3－11 钢桁架结构的节点它们都有一定的弹性变形，杆件的中心线也不可能是绝对直的，但上述三点假定已反映了实际桁架的主要受力特征，其计算结果可满足工程实际的需要。
分析静定平面桁架内力的基本方法有节点法和截面法，下面分别予以介绍。
一、节点法因为桁架中各杆都是二力杆，所以每个节点都受到平面汇交力系的作用，为计算各杆内力，可以逐个地取节点为研究对象，分别列出平衡方程，即可由已知力求出全部杆件的内力，这就是节点法。
由于平面汇交力系只能列出两个独立平衡方程，所以应用节点法往往从只含两个未知力的节点开始计算。
例3－8 平面桁架的受力及尺寸如图3－12ａ所示，试求桁架各杆的内力。
图3－12 例3－8图解：（1）求桁架的支座反力以整体桁架为研究对象，桁架受主动力2F以及约束反力、、作用，列平衡方程并求解：，＝０，２×－＝０，＝，＋－２＝０，＝2－=（2）求各杆件的内力设各杆均承受拉力，若计算结果为负，表示杆实际受压力。
理论力学桁架网络练习题一、基本概念题1. 请简述桁架结构的特点。
2. 桁架中的杆件主要承受哪种类型的载荷？3. 什么是节点？桁架中的节点有哪些类型？4. 简述静定桁架与超静定桁架的区别。
5. 桁架结构中的零杆具有什么性质？二、计算题1. 已知一简单桁架，各杆件的长度和材料相同，求各杆件的内力。
2. 计算如下图所示桁架结构中各杆件的内力（图中已给出各杆件长度和载荷）。
3. 有一静定桁架，部分杆件长度和载荷已知，求剩余杆件的长度。
4. 已知一超静定桁架，求各杆件的内力。
5. 分析下图所示桁架结构，判断其是否为静定桁架，并说明理由。
三、分析题1. 分析桁架结构在不同载荷作用下的受力特点。
2. 论述桁架结构在工程中的应用及其优缺点。
3. 比较分析不同材料桁架的受力性能。
4. 针对一个实际桁架工程案例，分析其设计合理性。
5. 讨论桁架结构在地震作用下的稳定性问题。
四、作图题1. 根据给定条件，绘制一个静定桁架的受力图。
2. 绘制一个超静定桁架的受力图，并标明各杆件的内力。
3. 根据下图所示桁架结构，绘制其节点载荷图。
4. 绘制一个桁架结构的弯矩图和剪力图。
5. 请绘制一个简支桁架在均布载荷作用下的受力图。
五、综合题2. 分析一个实际桁架结构，提出改进措施，使其受力更加合理。
3. 针对一个超静定桁架，采用力法求解各杆件的内力。
4. 讨论桁架结构在温度变化影响下的受力特点。
5. 结合工程实际，论述桁架结构在施工过程中的注意事项。
六、判断题1. 桁架结构中的杆件只能承受轴向力。
（）2. 所有桁架结构都必须是静定的。
（）3. 在桁架结构中，节点载荷可以分解为各杆件的轴力。
（）4. 超静定桁架的杆件内力可以通过静力平衡方程直接求出。
（）5. 桁架结构的稳定性只与杆件长度有关。
（）七、选择题A. 受拉杆件B. 受压杆件C. 零杆D. 弯曲杆件2. 桁架中的节点是：A. 杆件连接处B. 载荷作用点C. 支撑点D. 所有上述选项A. 杆件数量等于节点数减去支撑数B. 杆件数量等于节点数加上支撑数C. 载荷作用点等于节点数D. 支撑数等于节点数A. 力法B. 位移法C. 力矩分配法D. 直接平衡法5. 桁架结构的优化设计主要目的是：A. 减轻结构重量B. 提高结构稳定性C. 降低材料成本D. 所有上述选项八、填空题1. 桁架结构主要由______、______和______组成。
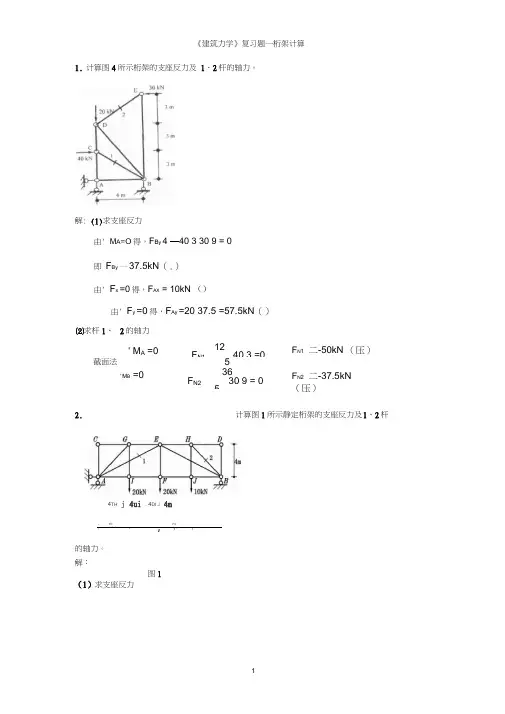
1. 计算图4所示桁架的支座反力及 1、2杆的轴力。
解: (1)求支座反力由' M A =O 得，F B y 4 —40 3 30 9 = 0即 F By 一37.5kN （.）由' F x =0得，F AX = 10kN （）由' F y =0得，F Ay =20 37.5 =57.5kN （）2. 计算图1所示静定桁架的支座反力及 1、2杆的轴力。
解：（1）求支座反力⑵求杆1、 2的轴力 ' M A =0 12 F N1 40 3 =0 截面法 5 36 F N2 30 9 = 0 5 ' M B =0 F N 1 二-50kN （压） F N 2 二-37.5kN （压）1 Pill 1 彳 Fill 1 * 1 1 11图14TH j 4ui . 4DI J 4m由' M A =0得，F By16 -10 12 -20 8 -20 4=0 即F By 二22.5kN（）由V F x =0得，F AX =0解:由' F y =0得，F A y = 50 — 22.5 = 27.5kN （） ⑵求杆1、2的轴力E M A =0截面法' M I =0 F NGE = 20 4 二 20kN （压） 4 15恋5 /十、 F N1 16.77kN （压） 2结点 H、、• F y =0F N 2『--10kN F N 2 - -10 . 2 - - 14.14kN （压） 3. 计算图1所示桁架的支座反力及 1、2杆的轴力。
图1解：（1）求支座反力由 V M A =0得，F By 4 30 12 =0 即 F By 二-90kN （-） 由 F x =0得，F AX =0由' F y =0 得，F Ay =90 30 =120kN （）（2）.求杆1、2的轴力卩阳二-90kN （压）F N2 - -50kN （压）4. 计算图所示桁架的支座反力及 1、2杆的轴力。
1. 计算图4所示桁架的支座反力及1、2杆的轴力。
解：
(1)求支座反力
由∑=0A M 得，09303404=⨯+⨯-⨯By F 即）（↓-=kN 5.37By F
由∑=0x F 得，)(kN 10←=Ax F
由∑=0y
F
得，）
（↑=+=kN 5.575.3720Ay F (2)求杆1、2的轴力
截面法
（压）
（压）
kN 5.370
930536
kN 500340512
02211-==⨯+⨯=-==⨯+⨯
=∑∑N N B
N N A F F M
F F M
2. 计算图1所示静定桁架的支座反力及1、2杆的轴力。
图1
解：
(1)求支座反力
由∑=0A M 得，0420820121016=⨯-⨯-⨯-⨯By F 即）（↑=kN 5.22By F 由
∑=0x
F
得，0=Ax F
由
∑=0y
F
得，）
（↑=-=kN 5.275.2250Ay F (2)求杆1、2的轴力
截面法
（压）
（压）kN 77.162
5150
kN 2044
200
1
-≈-==-=⨯-==∑∑N I
NGE A
F M
F M 结点H
kN 14.14210kN 10022-=⨯-=-==∑N y N y F F F （压）
3. 计算图1所示桁架的支座反力及1、2杆的轴力。
图1 解：
(1)求支座反力 (4分)
由∑=0A M 得，012304=⨯+⨯By
F 即）（↓-=kN 90By F
由
∑=0x F 得，0=Ax F
由∑=0y
F
得，）
（↑=+=kN 1203090Ay F (2).求杆1、2的轴力 (6分)
kN 901-=N F （压） kN 502-=N F （压）
4. 计算图所示桁架的支座反力及1、2杆的轴力。
解：
5.计算图所示桁架的支座反力及1、2杆的轴力。
解：
6.计算图所示桁架的支座反力及1、2杆的轴力。
解：
7.计算图所示桁架的支座反力及1、2杆的轴力。
解：。
