《建筑力学》第3章计算题
- 格式:doc
- 大小:1.90 MB
- 文档页数:17

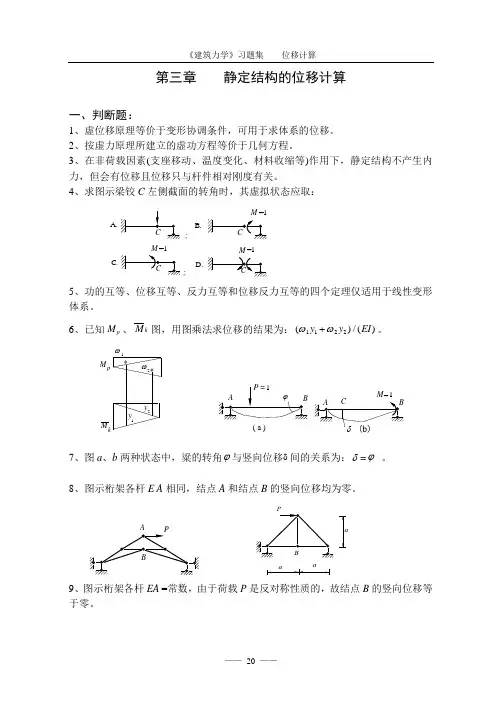
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形协调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A两侧截面的相对转角ϕA,EI = 常数。
q11、求图示静定梁D端的竖向位移∆DV。
EI = 常数,a = 2m 。
10kN/m12、求图示结构E点的竖向位移。
EI = 常数。
q13、图示结构,EI=常数,M=⋅90kN m, P = 30kN。
求D点的竖向位移。
P14、求图示刚架B端的竖向位移。
q15、求图示刚架结点C的转角和水平位移,EI = 常数。
q16、求图示刚架中D点的竖向位移。
EI = 常数 。
l/217、求图示刚架横梁中D点的竖向位移。
EI = 常数 。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l l/219、求图示结构A、B两截面的相对转角,EI = 常数 。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
21、求图示结构B 点的竖向位移,EI = 常数 。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
E I = 常数 ,垂直纸面取1 m 宽,水比重近似值取10 kN / m 3。



建筑力学第三章课后题答案一、选择题(每小题2分,共20分)1、“力”是物体之间相互的()。
[单选题] *A、机械运动B、机械作用(正确答案)C、冲击与摩擦D、连接作用2、由力的平移定理可知,一个力在平移时分解成为()。
[单选题] *A、一个力和一个力矩B、两个平行力C、一个力和一个力偶(正确答案)D、两个反向力3、两个大小相等的力偶()。
[单选题] *A、可以合成为一个合力偶(正确答案)B、是等效力偶C、对物体的作用效果相同D、可以合成为一个合力4、力偶向某坐标轴的投影为()。
[单选题] *A、力偶矩本身B、力偶中力的大小C、变化值D、零(正确答案)5、轴力的正负号规定为()。
[单选题] *A、拉为正,压为负(正确答案)B、拉为负,压为正C、均为正值D、均为负值6、Q235钢拉伸试验,材料经过弹性、屈服、强化、颈缩等四个阶段,其中三个特征点的应力依次为()。
[单选题] *A、比例极限、弹性极限、强度极限B、屈服极限、弹性极限、屈服极限C、比例极限、屈服极限、强度极限(正确答案)D、屈服极限、比例极限、强度极限7、有正方形、矩形、圆形三种截面,在面积相同的情况下,能取得最大惯性矩的截面是()。
[单选题] *A、正方形B、矩形(正确答案)C、圆形D、都有可能8、用叠加法作梁的弯矩图的前提条件是()。
[单选题] *A、梁的变形为小变形(正确答案)B、梁不发生变形C、梁内无剪力D、该梁必须为等截面梁9、均布荷载作用的直梁区段上,弯矩方程是截面位置坐标X的()次函数。
[单选题] *A、一次B、二次(正确答案)C、三次D、四次10、梁横截面上弯曲正应力为零的点发生在截面()。
[单选题] *A、最下端B、中性轴上(正确答案)C、最上端D、最大弯矩处二、判断题(每题1分,共10分)1、两个力大小相等,方向相反,则这两个力一定平衡。
[判断题] *对错(正确答案)2、两端用铰链连接的直杆,不一定是二力杆。


整理时间:2020.06.20 国开学习系统各章节本章自测之习题答案第一章习题01.建筑力学在研究变形固体时,对变形固体做了什么假设?A. 连续性假设02.杆件的基本变形包括()B. 轴向拉压、剪切、扭转、弯曲03.杆件轴向伸长或缩短的变形称为()C. 轴向拉压04. 杆件轴线变为曲线的变形()B. 弯曲05.建筑力学的研究对象是()C. 杆件结构06.工程结构必需满足以下哪种条件?()D. 强度条件、刚度条件、稳定性条件07.一般认为以下哪种材料是不符合各向同性假设的?( D )A. 金属B. 玻璃C. 陶瓷D. 木材08.基于( D )假设,可假设构成变形固体的物质没有空隙地充满整个固体空间。
选择一项:A. 小变形假设B. 各向同性假设C. 均匀性假设D. 连续性假设09.基于( B )假设,可假设变形固体中各处的力学性能是相同的。
选择一项:A. 各向同性假设B. 均匀性假设C. 连续性假设D. 小变形假设10.基于( D )假设,可假设材料沿任意方向具有相同的力学性能。
选择一项:A. 小变形假设B. 均匀性假设C. 连续性假设D. 各向同性假设1.根据荷载的作用范围不同,荷载可分为( D )。
选择一项:A. 永久荷载和可变荷载B. 恒荷载和活荷载C. 静荷载和动荷载D. 集中荷载和分布荷载2.关于柔索约束,以下说法正确的是( A )。
选择一项:A. 只能承受拉力,不能承受压力和弯曲B. 只能承受压力,不能承受拉力和弯曲C. 既能承受拉力,又能承受压力和弯曲D. 只能承受压力,不能承受拉力3.关于光滑圆柱铰链约束,以下说法不正确的是( C )。
选择一项:A. 不能限制物体绕销钉轴线的相对转动B. 不能限制物体沿销钉轴线方向的相对滑动C. 能限制物体绕销钉轴线的相对转动D. 只限制两物体在垂直于销钉轴线的平面内任意方向的相对移动4.只限制物体向任何方向移动,不限制物体转动的支座为( D )。
选择一项:A. 可动铰支座B. 固定支座C. 定向支座D. 固定铰支座5.既限制物体沿任何方向运动,又限制物体转动的支座称为( B )。

q l 22AM 图M 图(kN·m)2D习题3-1dq基本梁段受多荷载作用的叠加法—区段叠加法画弯矩图(1)区段叠加法原理:两端受集中力偶作用的简支梁,可以看成是从某梁中截取的一段。
该梁段两端的内力因暴露而成为“简支梁”的两端外力偶。
即,各区段可认为是两端受与两端弯矩值等值的“集中力偶”的“简支梁”。
(2)区段叠加法解题步骤: ①求支反力;②把梁分成若干段,使每一梁段只有单一的荷载作用。
当某段杆不用分段时,该段可采用微分法。
③求出各杆段两端的弯矩值并标在图上。
④用虚线连接杆段两端弯矩值的纵坐标的端点。
⑤采用与简支梁相同的方法画各区段的弯矩图。
1)区段受均布荷载:作杆段的中垂线与所连虚线交于某点,从该点沿均布载荷的方向量取82ql 得S 点;用细线连结虚线左端点、S 点、右端点,可得该杆段的弯矩图。
2)区段受集中荷载:作杆段的中垂线与所连虚线交于某点,从该点沿集中力的方向量取lPab得S 点;用细线连结虚线左端点、S 点、右端点,可得该区段的弯矩图。
当集力作用于区段的中点,则量取4Pl。
3)区段中点受集中力偶:作杆段的中垂线与所连虚线交于某点,从该点向上或向下量取lmb、l ma 得S 、S‘点;用细线连结虚线左端点、S 点、S‘、右端点,可得该区段的弯矩图。
当集力作用于区段的中点,则量取2m。
⑥各区段的弯矩图组合而成整个杆的弯矩图。
(3)注意:①图上要注明单位、控制面值、特殊点纵坐标值。
②梁上的结构示意图, 计算简图、剪力图和弯矩图要竖向排 列,清晰表达各自对应关系, 原图、内力图之间不要插入文字。
4.5M 图(kN·m)M 图(kN·m)25.5-+V 图(kN)-V 图(kN)96--++4713-2a :右伸臂部分没有荷载,其内力值为零。
本题采用叠加法,算出A 截面、C 左右截面、D 截面的弯矩值便可采用叠加法完成弯矩图。
))((15.012上拉m kN ⋅-=⨯⨯-=A M ))((5.624235.7下拉m kN 左⋅=⨯⨯-⨯=C M ))((5.93264235.7下拉m kN 右⋅=+⨯⨯-⨯=C M ))((5.4下拉m kN ⋅=D M——要求那个截面的内力,则可用一假想的截面把梁(或刚架)一刀两断,取某一部分来研究;解除所有的约束,代以约束反力,并把该截面视为“固定支座”,整个脱离体可视为悬臂梁(或悬臂刚架)。
《建筑力学》例题及解答第二章 平面杆件体系的几何组成分析对图示各体系分别作几何组成分析。
一、答题要点:( 共 10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)a 、大地及A 支座一起看成刚片Ⅰb 、BCF 看成刚片Ⅱc 、根据两刚片原则,刚片Ⅰ、Ⅱ通过三根不相交一点,且不完全平行的链杆AB 、EF 、CD 相连,组成无多余约束的几何不变体系。
二、答题要点:( 共 10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)a 、大地及A 支座一起看成大刚片Ⅰb 、ABEF 看成刚片,BCDG 看成刚片。
根据两刚片原则, 两刚片通过铰B 和不通过铰B 的链杆ED 相连,则ABCDE 可看成一个大刚片Ⅱ。
c 、根据两刚片原则,大刚片Ⅰ、Ⅱ通过铰A 和不通过铰A 的链杆CH 相连,为无多余约束的几何不变体系。
三、对图示各体系分别作几何组成分析。
答题要点:( 共10分)1、结论:整个体系为无多余约束的几何不变体系。
( 4分)2、分析要点:( 6分)A B C DE F A B C DE F G H (a)(b)(a)F E D CB A ⅠⅡBC D EF A B C EF G H (a)(b)(b)H G F E D CBA ⅠⅡA B C D E H I J (a)F A B C D E G H I J K (b)123ⅡⅠO 2O 1(a)J I H E D C B Aa 、将ABC 、CDE 、IH 分别看成钢片1、2、3b 、1、2刚片-用铰C 相连;1、3刚片用虚铰O 2相连(AF 、AH 延长线的交点);2、3刚片用虚铰O 1相连(DI 、EH 延长线的交点)。
三铰不共线,根据三刚片原则,ABCDEH 为无多余约束的內部几何不变体系,可看成大钢片Ⅰ。
c 、大地及A 支座一起看成刚片Ⅱ,刚片Ⅰ、Ⅱ通过铰A 和不通过铰A 的链杆EJ 相连,,根据两刚片原则,可判断整个体系为无多余约束的几何不变体系。
《建筑力学》第三章复习题一、名词解释。
1、轴向拉伸:2、轴向压缩:3、内力:4、应力:二、填空题。
1、确定截面上内力的基本方法是。
2、根据梁的强度条件可以解决有关强度等方面的三类问题,一是,二是,三是。
3、当杆件受拉而伸长时,轴力背离截面,轴力取值,反之取值。
4、是杆件轴向分布内力的合力。
轴力的大小与有关,与杆件截面尺寸和无关。
5、应力最大的截面叫做。
6、正应力的符号与相同,拉应力为,压应力为。
7、如图所示杆件M—M截面的轴力为。
8、在弹性范围内,应力和应变成9、在计算简图中,一般把节点简化为和10、正应力的符号与轴力相同,拉应力为,压应力为。
三、判断题。
1、内力是指杆件内部各部分间的相互作用力。
()2、内力的大小与杆件的强度和刚度及杆件截面尺寸有关。
()3、轴力是杆件轴向分布内力的合力。
()4、单位面积上的内力叫做应力。
()5、轴力的大小与外力、截面尺寸有关,而与材料无关。
()6、为保证杆件安全正常工作,不致发生破坏,必须规定杆件工作的最高限度。
()7、用截面法将杆件截成两部分,左、右两部分所得的结果不仅数值相等而且正负号相同。
()8、对于任何受力物体,都存在关系()9、工程结构和构件在外力作用下,丧失正常的功能的现象,称为失效。
()10、在几何不变体系上增加或减去一个二元体,得到的体系仍然是几何不变体系。
()11、对于多跨静定梁,当荷载作用在附属部分上时,其基本部分的杆件不受力。
()三、选择题。
1、影响轴力大小的因素是()A、外力B、截面尺寸C、材料D、内力2、当杆件工作应力超过一定的限度时,杆件就要破坏,发生破坏的应力限度是()A、工作应力B、极限应力C、许用应力D、内力3、截面法求杆件内力的步骤有()A、切开B、代替C、平衡D、计算4、图示受力杆件N—N截面的轴力等于()。
A、2PB、-3PC、6PD、P5、下列体系中可作为结构的是()A、几何不变体系;B、几何可变体系;C、瞬变体系;6、1Mpa不等于()A、106N/m2;B、1N/mm2;C、106pa;D、103 N/m7、轴力图按规定应把正轴力画在轴的哪一侧()A、上侧;B、下侧;C、哪侧都行五、计算题:1、混凝土桥墩要求承受400KN的轴向压力,桥墩的截面面积为400×600mm2,许用应力[σ]=6Mpa;试校核其强度2、如图,杆AB为直径d=30mm钢杆,其[σ]=160Mpa;杆BC为宽b=50mm高度h=100mm 的矩形木杆,其[σ]=8Mpa;承受荷载p=80Kn,试校核结构的强度。
《建筑⼒学》第3章计算题计算题( 第三章 )3.l ⽤⼏何法求图⽰汇交⼒系的合⼒。
1100F N =,280F N =,3120F N =,4160F N =。
3.2 ⼀个固定环受到三根绳索的拉⼒,1 1.5T F kN =,2 2.2T F kN =,31T F kN =,⽅向如图题3.2所⽰,求三个拉⼒的合⼒。
3.3 图题3.3⽰⼀平⾯⼒系,已知110F N =,225F N =,340F N =,416F N =,514F N =,求⼒系向O 点简化的结果。
图中每⼩格边长为1m 。
3.4重⼒坝受⼒情形如图题 3.4⽰,设坝的⾃重分别为19600G F kN =,221600G F kN =,上游⽔压⼒10120P F kN =,试将⼒系向坝底O 点简化,并求其最后的简化结果。
3.5 试⽤解析法求图题3.5⽰两斜⾯的反⼒NA F 和NB F ,其中匀质球重500G F N 。
3.6 梁AB的⽀座如图题3.6所⽰。
在梁的中点作⽤⼀⼒20PF kN,⼒和梁的轴线成45 。
如梁的⾃重忽略不计,分别求(a)、(b )两种情况下⽀座反⼒。
⽐较两种情况的不同结果,你得到什么概念?3.7 求图⽰各梁的⽀座反⼒。
3.8 求图题3.8⽰各梁的⽀座反⼒。
3.9 求图⽰多跨静定梁的⽀座反⼒。
3.10 图题 3.10所⽰多跨静定梁AB 段和BC 段⽤铰链B 连接,并⽀承于连杆1、2、3、4上,已知6AD EC m ==,8AB BC m ==,60α= ,4a m =,150P F kN =,试求各连杆所受的⼒。
3.11 多跨梁上的起重机,起重量10W F kN =,起重机重50G F kN =,其重⼼位于铅垂线EC 上,梁⾃重不计。
试求A 、B 、D 三处的⽀座反⼒。
3.12 求图⽰各梁的⽀座反⼒。
题3.12图3.13 已知挡⼟墙重F G1=90kN,垂直⼟压⼒F G2=140kN,⽔平压⼒F=100kN,试验算此挡⼟墙是否会倾覆?题3.13图题3.14图3.14 如图⽰,⼯⼈启闭闸门时,为了省⼒,常将⼀根杆穿⼊⼿轮中,并在杆的⼀端C加⼒,以转动⼿轮。
计 算 题( 第三章 )
用几何法求图示汇交力系的合力。
1100F N =,280F N =,3120F N =,4160F N =。
一个固定环受到三根绳索的拉力,
1 1.5T F kN =,
2 2.2T F kN =,31T F kN =,方向如图题所示,求三个
拉力的合力。
图题示一平面力系,已知110F N =,225F N =,340F N =,416F N =,514F N =,求力系向O 点简化的结果。
图中每小格边长为1m 。
重力坝受力情形如图题示,设坝的自重分别为19600G F kN =,221600G F kN =,上游水压力10120P F kN =,试将力系向坝底O 点简化,并求其最后的简化结果。
试用解析法求图题示两斜面的反力
NA F 和NB F ,其中匀质球重500G F N 。
梁AB的支座如图题所示。
在梁的中点作用一力
20
P
F kN
,力和梁的轴线成45。
如梁的自重忽略不计,
分别求(a)、(b )两种情况下支座反力。
比较两种情况的不同结果,你得到什么概念求图示各梁的支座反力。
求图题示各梁的支座反力。
求图示多跨静定梁的支座反力。
图题所示多跨静定梁AB 段和BC 段用铰链B 连接,并支承于连杆1、2、3、4上,已知6AD EC m ==,8AB BC m ==,60α=,4a m =,150P F kN =,试求各连杆所受的力。
多跨梁上的起重机,起重量
10
W
F kN
=
,起重机重
50
G
F kN
=
,其重心位于铅垂线EC上,梁自重不计。
试求A、B、D三处的支座反力。
求图示各梁的支座反力。
题图
已知挡土墙重F G1=90kN,垂直土压力F G2=140kN,水平压力F=100kN,试验算此挡土墙是否会倾覆
题图题图
如图示,工人启闭闸门时,为了省力,常将一根杆穿入手轮中,并在杆的一端C加力,以转动手轮。
设杆长l=1.4m,手轮直径D=0.6m。
若在C端加力F=100N能将闸门开启,问不用杆而直接在手轮A、B处施加力偶(F,F′),则力F至少多大才能开启闸门
图示四连杆机构ABCD,杆AB和CD上各作用一力偶,使机构处于平衡状态。
已知:m1=1N·m,CD=400mm,AB=600mm,
各杆自重不计。
求作用在杆AB的力偶矩m2及杆BC
所受的力。
图题
求图示各梁的支座反力。
图题
楼梯的两端支在两个楼梯梁上(图a)上端B可视为光滑接触,下端A可视为铰连接,所受的荷载连同楼
梯自重可视为沿楼梯的长度均匀分布,设荷载的集度
kN/m
7
q,试求楼梯两端A、B的约束反力。
图题求图示刚架的支座反力。
图题
试求图示桁架的支座反力。
图题
某厂房柱,高9m,柱的上段BC重F G1=10kN,下段CA重F G2=40kN,风力q=m,柱顶水平力F Q=6kN,各力作用位置如图所示,求固定端支座A的反力。
图题 图题
图示上料小车重F G =10kN ,沿着与水平成︒60的轨道匀速提升,料车的重心在C点。
试求提升料车的牵引力F T 和料车对轨道的压力。
塔式起重机,重F G =500kN (不包括平衡锤重量F Q ),如图示。
跑车E 的最大起重量F P =250kN ,离B 轨的最远距离m 10=l ,为了防止起重机左右翻倒,需在D 点加一平衡锤,要使跑车在空载和满载时,起重机在
任何位置不致翻倒,求平衡锤的最小重量和平衡锤到左轨A 的最大距离。
跑车自重包含在F P 中,且m 5.1=e ,m 3 =b 。
图题 图题
AB杆重kN 5.7,重心在杆的中点。
已知F G =8kN,AD=AC=4.5m,BC=2m ,滑轮尺寸不计。
求绳子的拉力和支座A的反力。
图示厂房结构为三铰拱架,吊车横梁的重量kN 12,作用在桥中间,吊车重8kN ,左、右拱架各重60kN ,风压的合力为12kN ,求支座A 、B 的约束反力。
图题求图示两跨静定刚架的支座反力。
图题
图示构架,不计自重,A 、B 、D 、E 、F 、G 都是铰链,设F 1=5kN,F 2=3kN ,m 2=a ,试求铰链G 和杆ED 所受的力。
图题 图题
图示一台秤,空载时,台秤及其支架BCE 的重量与杠杆AB 的重量恰好平衡;当秤台上有重物时,在AO 上加一重F W 的秤锤,a =OB ,求AO 上的刻度x 与重量F Q 之间的关系。
剪断钢筋的设备如图示。
欲使钢筋E 受到12kN 的压力,向加在A 点的力应为多大图中尺寸单位为cm 。
图题 图题
图示水平梁AB 由铰链A 和杆BC 所支持,在梁上D 处用销子安放半径为m 1.0=r 的滑轮,已知F Q =2kN,AD=0.2m,BD=0.4m,045=α
,不计梁、杆、滑轮的重量,试求铰链A 和杆BC 对梁的反力。
下撑式屋架结构及荷载如图所示。
求支座A 、B 的约束力及1、2、3、4、5杆的内力。
图题
梁AE 由直杆连接支承于墙上,如图示,受荷载m kN q 8 作用,不计杆重,求A 、B 的约束反力及1、2、3杆所受到的力。
图题 图题
图示梯子,A 点为铰接,梯子放在光滑的水平面上,在AC 部分上作用一铅垂力F ,不计梯重。
求梯子平衡时,绳DE 的拉力。
设a 、l 、h 、α均为已知。
部分参考答案
2.87R kN = 559α'=
41.13R N = 1.65m N m =-
32800R kN = 72.03α= 18.97d m =
366A N N = 450B N N =
(a) 15.8A R kN = 7.1B R kN =
(b) 22.4A R kN = 10B R kN =
(a) ()7.07A X kN = ()12.07A Y kN = ()38.28A m kN m =
(b) 0A X = (
)42A Y kN = ()2B Y kN = (c) 0A X = ()0.25A Y qakN = ()1.75B Y qakN =
(a) 0A X = ()3.75A Y kN = ()0.25B Y kN =
(b) 0A X = (
)25A Y kN = ()20B Y kN = (c) 0A X = (
)132A Y kN = ()168B Y kN = (a) 0A X = ()4.84A Y kN = ()17.51B R kN = ()5.33D R kN =
(b) 0A X = (
)6A Y kN = ()16A m kN m = ()18C R kN =
162.5()R kN = 257.34()R kN = 357.34()R kN = 412.41()R kN =
0A X = (
)48.33A Y kN = ()100B R kN = ()8.33D R kN =。