下载文档原格式
第一章绪论1.1 建筑力学的研究对象1.(单选题) 下列结论中，哪些不正确？（）（A）力偶的合力不为零；（B）力偶是一对力；（C）力偶矩与矩心的位置无关；（D）力偶作用的效果是使物体产生转动。
参考答案：C2.(单选题) 平面上的合力对该平面内一点的矩（）（A）大于其各分力对该点的矩的代数和（B）等于其各分力对该点的矩的代数和（C）小于其各分力对该点的矩的代数和（D）有时大于、有时小于其各分力对该点的矩的代数和参考答案：B1.2 建筑力学的任务1.(单选题) 力的可传性原理是指作用于刚体上的力可在不改变其对刚体的作用效果下（）（A）平行其作用线移到刚体上任一点（B）沿其作用线移到刚体上任一点（C）垂直其作用线移到刚体上任一点（D）任意移动到刚体上任一点参考答案：B1.3 刚体、变形体及其基本假设1.(单选题) 既有大小，又有方向的物理量称为（）A．矢量B．代数量C．标量D．以上皆不是参考答案：A2.(单选题) 材料力学的研究对象是（）A．刚体B．变形体C．塑形固体D．弹性固体参考答案：B1.4 杆件变形的基本形式1.(单选题) 以下哪一个不属于结构杆件的基本受力形式（）A．压缩B．失稳C．扭转D．弯曲参考答案：B1.5 荷载的分类1.(单选题) 光滑面对物体的约束力，作用在接触点处，方向沿接触面的公法线，且（）（A）指向受力物体，恒为拉力（B）指向受力物体，恒为压力（C）背离受力物体，恒为拉力（D）背离受力物体，恒为压力参考答案：B2.(单选题) 荷载按作用范围可分为（）A．分布和在和集中荷载B．恒荷载和活荷载C．静力荷载和动力荷载D．以上皆不是参考答案：A第二章静力学基础2.1 力、力矩及其性质1.(单选题) 力的大小、方向、作用点称为（）A．力的等效性B．力的平衡条件C．力的三要素D．以上皆不是参考答案：C2.(单选题)参考答案：A3.(单选题) 当力的作用线通过矩心时，则力矩的大小为（）A．正值B．零C．负值D．不一定参考答案：B2.2 约束与约束反力1.(单选题) 作用于同一物体上的荷载与什么组成平衡力系（）A．作用力B．约束反力C．约束D．内力参考答案：B2.(单选题) 定向支座的约束力是（）。
第七章平面图形的几何性质研究截面几何性质的意义从上章介绍的应力和变形的计算公式中可以看出，应力和变形不仅与杆的内力有关，而且与杆件截面的横截面面积A、极惯性矩I P、抗扭截面系数W P等一些几何量密切相关。
因此要研究构件的的承载能力或应力，就必须掌握截面几何性质的计算方法。
另一方面，掌握截面的几何性质的变化规律，就能灵活机动地为各种构件选取合理的截面形状和尺寸，使构件各部分的材料能够比较充分地发挥作用，尽可能地做到“物尽其用”，合理地解决好构件的安全与经济这一对矛盾。
第一节 静矩一、静距的概念Ay S z d d =Az S y d d =⎰⎰⎰⎰====AAy y AAz z Az S S A y S S d d d d zy d A yz静距是面积与它到轴的距离之积。
平面图形的静矩是对一定的坐标而言的，同一平面图形对不同的坐标轴，其静矩显然不同。
静矩的数值可能为正，可能为负，也可能等于零。
它常用单位是m 3或mm 3。
形心d A zyy zCx Cy ⎪⎪⎭⎪⎪⎬⎫⋅∆∑=⋅∆∑=A y A y Az A z C C ⎪⎪⎭⎪⎪⎬⎫==⎰⎰A ydA y A zdA z AC A C ⎪⎪⎭⎪⎪⎬⎫==A S y A S z z C y C ⎭⎬⎫⋅=⋅=C y C z z A S y A S 平面图形对z 轴（或y 轴）的静矩，等于该图形面积A 与其形心坐标y C （或z C ）的乘积。
当坐标轴通过平面图形的形心时，其静矩为零；反之，若平面图形对某轴的静矩为零，则该轴必通过平面图形的形心。
如果平面图形具有对称轴，对称轴必然是平面图形的形心轴，故平面图形对其对称轴的静矩必等于零。
⎭⎬⎫⋅=⋅=C y C z z A S y A S二、组合图形的静矩根据平面图形静矩的定义，组合图形对z 轴（或y 轴）的静矩等于各简单图形对同一轴静矩的代数和，即⎪⎪⎭⎪⎪⎬⎫=+++==+++=∑∑==ni Ci i Cn n C C y ni Ci i Cn n C C z z A z A z A z A S y A y A y A y A S 1221112211 式中 y Ci 、z Ci 及A i 分别为各简单图形的形心坐标和面积;n 为组成组合图形的简单图形的个数。
第7章静定结构的内力分析在进行结构设计时，应保证结构的各个构件能正常地工作，即构件应具有一定的强度、刚度和稳定性。
要解决强度、刚度和稳定性问题，必须首先确定构件的内力。
内力是物体内部之间的相互作用力。
内力计算是建筑力学的重要基础知识，也是进行结构设计的重要环节。
本章将讨论静定结构和构件的内力计算问题。
7.1 工程中梁弯曲的概念7.1.1梁平面弯曲的概念工程结构中常用梁来承受荷载。
例如，如图7.1(a)和图7.2(a)为房屋建筑中的楼面梁和阳台悬挑梁等。
这些荷载的方向都与梁的轴线相垂直，在载荷作用下，梁要变弯，其轴线由原来的直线变成了曲线。
以轴线变弯为主要特征的变形形式称为弯曲变形或简称弯曲。
以弯曲为主要变形的杆件称为梁，通常用轴线代表梁。
图7.1（b）和图7.2（b)分别为楼面梁和阳台挑梁的简图，并画出了梁弯曲后的形状示意图。
产生弯曲变形的构件称为受弯构件。
工程中梁的横截面通常采用对称形状，如矩形、工字形、T形以及圆形等。
横截面一般具有一竖向对称轴，该轴与梁轴线构成梁的纵向对称面。
当梁上所有外力均作用在纵向对称面内时，变形后的梁轴线也仍在纵向对称平面内，如图7.3所示。
这种在变形后梁的轴线所在平面与外力作用面重合的弯曲称为平面弯曲。
平面弯曲是弯曲变形中最简单和最基本的情况，也是工程中最常见的。
本章讨论只限于平面弯曲情况。
7.1.2单跨静定梁的类型梁的约束反力能用静力平衡条件完全确定的梁，称为静定梁。
根据约束情况的不同，单跨静定梁可分为以下三种常见形式：（1）简支梁。
梁的一端为固定铰支座，另一端为可动铰支座，如图7.4（a)(2) 悬臂梁。
梁的一端固定，另一端自由，如图7.4(b)。
(3) 外伸梁。
简支梁的一端或两端伸出支座之外，如图7.4(c)。
图7.4是梁的简化计算简图，作用在梁上的外力，包括梁上的荷载和支承梁的约束反力，一般是已知的，约束反力可由平衡方程求出，在这些外力求出后，就可以讨论梁的内力计算。
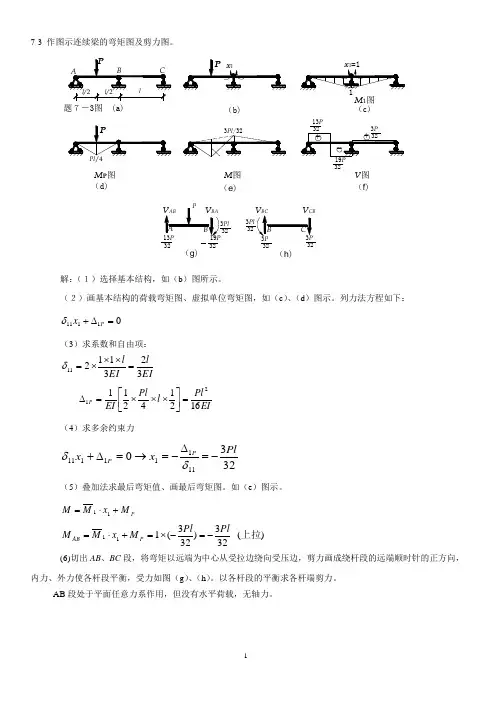
7-3 作图示连续梁的弯矩图及剪力图。
3232（g )32（h )（d)M P 图题７－3图(a)13P 32V 图（f )M 图（e )M 1图（c)（b)解：（１）选择基本结构，如（b ）图所示。
（２）画基本结构的荷载弯矩图、虚拟单位弯矩图，如（c ）、（d ）图示。
列力法方程如下：01111=∆+P x δ（3）求系数和自由项：EIlEI l 32311211=⨯⨯⨯=δ EI Pl l Pl EI P1621421121=⎥⎦⎤⎢⎣⎡⨯⨯⨯=∆ （4）求多余约束力323011111111Plx x PP -=∆-=→=∆+δδ（5）叠加法求最后弯矩值、画最后弯矩图。
如（e ）图示。
P M x M M +⋅=11)(323)323(111上拉PlPl M x M M P AB -=-⨯=+⋅= (6)切出AB 、BC 段，将弯矩以远端为中心从受拉边绕向受压边，剪力画成绕杆段的远端顺时针的正方向，内力、外力使各杆段平衡，受力如图（g ）、（h ）。
以各杆段的平衡求各杆端剪力。
AB 段处于平面任意力系作用，但没有水平荷载，无轴力。
⎪⎪⎩⎪⎪⎨⎧=+=-=--=→⎪⎩⎪⎨⎧=--=⋅--⋅-→==∑∑32133219232300232300P V P V P P P V V P V l P Pl l V Y M BA AB BA BA AB BA ABC 段处于平面力偶系作用而平衡，没有水平荷载，无轴力：32303230PV V l V Pl M CB BC BC ==→=⋅-→=∑。
7-5 作图示刚架的的弯矩图、剪力图、轴力图。
题7-5(a)图Pl 461P 11623211661P BC 11655N (h )19P解：（１）选择基本结例构，如（b ）图示。
（２）画基本结构的荷载弯矩图、虚拟单位弯矩图，如（c ）、（d ）、(e)图示。
列力法方程如下：⎩⎨⎧=∆+⋅+⋅=∆+⋅+⋅022221211212111P P x x x x δδδδ （3）求系数和自由项：232111522222216Pl Pl l Pl Pl l E I EI EI∆=-⨯⨯⨯⨯+⨯⨯=⋅32111211532222332296P l Pl l l Pl Pl l E I EI EI⎛⎫∆=-⨯⨯⨯⨯+⨯-⨯⨯=-⎪⋅⎝⎭32311117326l l l l E I EI EIδ=⨯⨯+⨯=⋅331221113()2224l l l l l E I EI EI δδ==-⨯⨯⨯-⨯=-⋅ 3333223223l l l l E I E I EI EIδ=++=⋅⋅（4）求多余约束力1211227353610()6496116351910()416232P P x x x P P x x x ⎧⎧⋅-⋅-==↑⎪⎪⎪⎪→⎨⎨⎪⎪-⋅+⋅+==→⎪⎪⎩⎩（5）叠加法求最后弯矩值、画最后弯矩图。
整理时间：2020.06.20 国开学习系统各章节本章自测之习题答案第一章习题01.建筑力学在研究变形固体时，对变形固体做了什么假设？A. 连续性假设02.杆件的基本变形包括（）B. 轴向拉压、剪切、扭转、弯曲03.杆件轴向伸长或缩短的变形称为（）C. 轴向拉压04. 杆件轴线变为曲线的变形（）B. 弯曲05.建筑力学的研究对象是（）C. 杆件结构06.工程结构必需满足以下哪种条件？（）D. 强度条件、刚度条件、稳定性条件07.一般认为以下哪种材料是不符合各向同性假设的？（ D ）A. 金属B. 玻璃C. 陶瓷D. 木材08.基于（ D ）假设，可假设构成变形固体的物质没有空隙地充满整个固体空间。
选择一项：A. 小变形假设B. 各向同性假设C. 均匀性假设D. 连续性假设09.基于（ B ）假设，可假设变形固体中各处的力学性能是相同的。
选择一项：A. 各向同性假设B. 均匀性假设C. 连续性假设D. 小变形假设10.基于（ D ）假设，可假设材料沿任意方向具有相同的力学性能。
选择一项：A. 小变形假设B. 均匀性假设C. 连续性假设D. 各向同性假设1.根据荷载的作用范围不同，荷载可分为（ D ）。
选择一项：A. 永久荷载和可变荷载B. 恒荷载和活荷载C. 静荷载和动荷载D. 集中荷载和分布荷载2.关于柔索约束，以下说法正确的是（ A ）。
选择一项：A. 只能承受拉力，不能承受压力和弯曲B. 只能承受压力，不能承受拉力和弯曲C. 既能承受拉力，又能承受压力和弯曲D. 只能承受压力，不能承受拉力3.关于光滑圆柱铰链约束，以下说法不正确的是（ C ）。
选择一项：A. 不能限制物体绕销钉轴线的相对转动B. 不能限制物体沿销钉轴线方向的相对滑动C. 能限制物体绕销钉轴线的相对转动D. 只限制两物体在垂直于销钉轴线的平面内任意方向的相对移动4.只限制物体向任何方向移动，不限制物体转动的支座为（ D ）。
选择一项：A. 可动铰支座B. 固定支座C. 定向支座D. 固定铰支座5.既限制物体沿任何方向运动，又限制物体转动的支座称为（ B ）。
计算题( 第七章 )
7.1 求下列各梁指定截面上的剪力FQ和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
7.2试列出下列各梁的剪力方程和弯矩方程。
并作出剪力图和弯矩图。
题5.21图
7.3 用叠加法作以下列各梁的弯矩图。
并求出∣M∣max。
7.4 作下列各梁的剪力图和弯矩图。
7.5图示外伸梁，承受均布荷载q作用。
试问当a为何值时梁的最大弯矩值（即∣M∣max）最小。
7.6作图示刚架的内力图。
7.7作图示静定多跨梁的剪力图和弯矩图。
7.8作图示圆弧拱的支座反力，并K截面的内力（轴力、剪力和弯矩）。
7.9 求图示平面桁架各杆的内力。
7.10 求图示平面桁架指定杆1、2、3、4的内力。
7.11 试作图示多跨静定梁的M及Q图。
题7.11图7.12 试作图示多跨静定梁的M图。
题7.12图
7.13 试作图示多跨静定梁的M图。
题7.13图
7.15 快速作出下列图示刚架M图。
7.16 作下列斜梁的M图。
7.17 指出下列桁架中的零杆，并求指定杆的内力。
7.18 图a和图b两个抛物线三铰拱，其拱轴方程为：
()x
l x
l
f
y-
=
2
4
，跨度相同，拱高不同，左半跨受
相同的均布荷载作用，如图所示。
求其竖向支座反力、水平推力H和左、右四分之一跨度处截面K1、K2的弯矩。
题7.18图
7.19试计算图示组合结构。
作出其中梁式杆的M图，并求出各链杆的轴力。
题7.18图
部分参考答案
7.1 （a ） 2332222118
3
,2;8,2;8,2ql M ql F ql M ql F ql M ql F Q Q Q -=-=-=-=-
=-= (b) 0,3
2;92,32;92,3332211=-==-===
M F F Fl M F F Fl M F F Q Q Q (c) 2
,;82,22
22211ql Fl M Fl F F ql Fl M ql F F Q Q --=+=--=+=
(d) 32,;3,2211m M l m F m M l m F Q Q -====
(e) 2
,;2,22211Fl M F F Fl M F F Q Q -==-=-
= (f) 8
,8;8,22
22211ql M ql F ql M ql F Q Q -==-=-=
7.2 (a) 2
,2
max
max
ql M
ql F Q
== (b) m M F Q ==max
,0
(c) Nm M N F Q 950,200max
max
==
(d) m M l
m F Q ==
max
max
,
(e) Nm M N F Q 356,2670max
max
== (f) F l
a
a l M F l
a
l F Q )2(,2max
max
-=
-=
(g) Fa M F F Q ==max
max
,
(h) m N M N F Q ⋅==10,50max
max
(i) 2,2max
max
qa M
qa F Q
==
(j) 2
,45
2max
max
qa M qa F Q
==
7.3 (a) 4
3max
Fa
M
=
(b) 82max
ql M = 7.4 (a) Fa M
F F Q
3,2max
max
==
(b) 2max
max
,2qa M
qa F Q ==
(c) 128
9,83
2max
max
ql M ql F Q == (d) Fa M
F F Q ==max
max
,
(e) 3625,45
2max
max
qa M qa F Q
==
(f) 4
3,23
2max
max
qa M qa F Q ==
(g) 2max
max
,qa M
qa F Q ==
(h) 6
5,6
7
2max
max
qa M qa F Q
==
7.5 l a 207.0=
7.6 (d) m kN M m kN M CB BA ⋅=⋅=10,10
kNm M M m kN M D C CD 8.16,0,10max ==⋅=
7.8 kN F kN F m kN M NK Q K k 3.68,3.18,29-==⋅-= 7.10 （a ）0,3,2,24321==-=-=N N N N F F F F F F F
(b)0,21=-=N N F F F (c) F F F N N 3
2
,021-
== (d) kN F N 3
5
101-
=。
