下载文档原格式
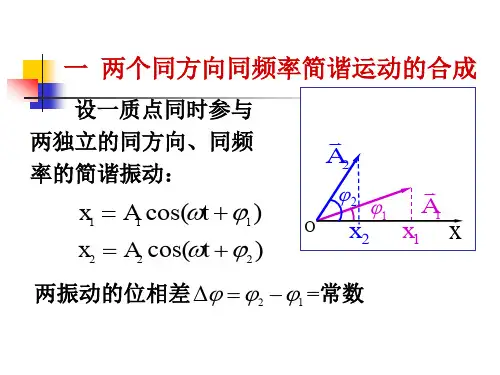
波的合成公式波的合成公式是物理学中用来描述两个或多个波同时存在时，它们叠加形成的新波的数学表达式。
在波动光学、声学以及其他许多领域中，波的合成是一个重要的概念。
波的合成公式取决于波的性质和合成方式。
下面将介绍几种常见的波的合成公式。
1. 相干波的合成：在相干波的合成中，当两个波的相位差恒定时，它们将产生干涉现象。
这种情况下，合成波的振幅是两个波的振幅的矢量和。
假设有两个波源的振幅分别为 A1 和 A2，它们之间的相位差为Δφ，那么合成波的振幅可以表示为：A = √(A1² + A2² + 2A1A2cosΔφ)2. 不相干波的合成：在不相干波的合成中，各个波之间的相位差是随机的，无法产生干涉现象。
在这种情况下，合成波的振幅是每个波的振幅的平方和的平方根。
假设有两个波源的振幅分别为 A1 和 A2，那么合成波的振幅可以表示为：A = √(A1² + A2²)3. 单色光的合成：在单色光的合成中，可以利用标称波长及相位差来描述两个或多个单色光的合成波。
假设有两个单色光的波长分别为λ1 和λ2，它们之间的相位差为Δφ，那么合成波的波长可以按照光的干涉公式表示为：λ = (λ1λ2)/(λ1 - λ2) * sin(Δφ/2)4. 双音定位的合成：在双音定位中，可以利用两个音源之间的时间差来描述合成声音的方向。
假设两个音源分别位于距离听者 L1 和 L2 处，合成声音的速度为 v，那么合成声音的时间差可以表示为：Δt = (L1 - L2)/v上述是几种常见的波的合成公式，它们基于不同的物理原理和条件而产生。
在应用中，我们可以根据具体情况选择合适的合成公式来描述波的行为和特性。
总结起来，波的合成公式为物理学家研究波的相互作用和性质提供了重要的数学工具。
通过运用合适的公式，我们可以准确地描述和预测波的行为，从而推动物理学和其他相关领域的发展。
波的合成原理及应用1. 引言波的合成是指两个或多个波相互作用形成一个新的波的过程。
在物理学中，波的合成原理和应用广泛，涉及到光学、声学以及电磁学等领域。
了解波的合成原理和应用可以帮助我们更好地理解和应用这一重要的物理现象。
2. 波的合成原理波的合成原理可以通过以下几种方式实现：2.1. 直接叠加法直接叠加法是最简单的波的合成方法之一。
当两个波在同一时刻、相近的位置上相遇时，它们的振动会叠加在一起形成一个新的波。
2.2. 干涉法干涉法是波的合成中常用的方法之一。
当两个或多个波同时通过一定的路径到达同一位置时，它们会相互干涉产生干涉图样。
干涉法可以分为衬比干涉和光栅干涉等。
2.3. 叠加法叠加法是将多个波叠加在一起，根据它们的振幅、频率、相位等性质来生成合成波。
3. 波的合成应用波的合成在多个领域中有着重要的应用。
以下列举了一些常见的应用：3.1. 音频信号处理在音频信号处理中，波的合成被广泛应用于声音的合成和音乐合成。
通过合成不同频率、振幅和相位的波，可以生成各种不同的音色和声音效果。
3.2. 光学干涉仪光学干涉仪是利用光的干涉原理来测量和分析光的性质。
通过合理设计光学元件，可以使两束或多束光波相互干涉，从而产生干涉图样，通过观察和分析干涉图样可以得到有关光的信息。
3.3. 电磁波合成天线在无线通信中，电磁波合成天线被用于将多个天线的信号合成成一个单一的信号。
通过合成不同方向的波，可以实现波束成型和多天线通信。
3.4. 模拟合成孔径雷达模拟合成孔径雷达（SAR）是一种利用合成孔径成像技术来获取地面目标信息的雷达系统。
通过合成多个雷达波的回波信号，可以获得高分辨率的地面目标图像。
3.5. 声波成像在医学影像学中，声波成像被广泛应用于超声波检查。
通过合成不同方向和频率的声波，可以形成目标的图像，从而进行疾病的诊断和治疗。
4. 结论波的合成是一种重要的物理现象，广泛应用于光学、声学以及电磁学等领域。
通过了解波的合成的原理和应用，我们可以更好地理解和应用这一物理现象，推动科学技术的发展。
