5-2平面简谐波的波动方程详解

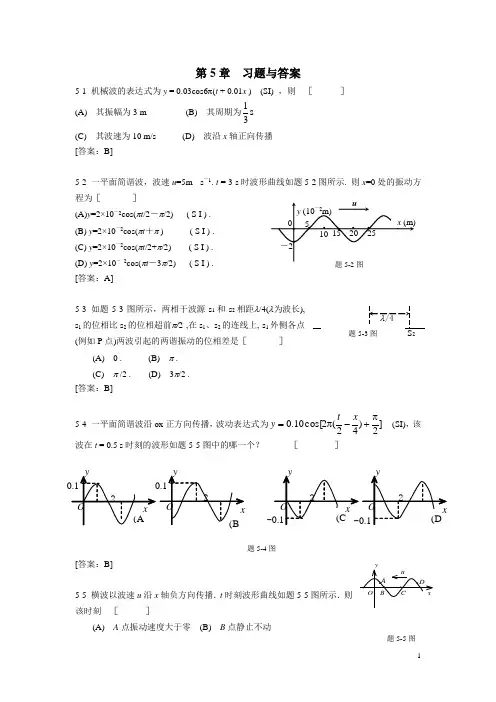
第5章 习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则［ ］ (A) 其振幅为3 m(B) 其周期为s 31(C) 其波速为10 m/s (D)波沿x 轴正向传播 [答案：B]5-2 一平面简谐波，波速u =5m · s －1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为［ ］(A)y =2×10－2cos(πt /2－π/2) ( S I ) . (B) y =2×10－2cos(πt ＋π ) ( S I ) . (C) y =2×10－2cos(πt /2+π/2) ( S I ) .(D) y =2×10－ 2cos(πt －3π/2) ( S I ) .[答案：A]5-3 如题5-3图所示，两相干波源s 1和s 2相距λ/4(λ为波长), s 1的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是［ ］(A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案：B]5-4 一平面简谐波沿ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个？ ［ ］[答案：B]5-5 横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如题5-5图所示．则该时刻 ［ ］(A) A 点振动速度大于零 (B) B 点静止不动ux (m)y (10－2m)· · · · · · · 0 51015 20 25 －2题5-2图题5-4图题5-5图-(C) C 点向下运动 (D) D 点振动速度小于零 [答案：D]5-6 一平面简谐波沿x 轴正方向传播，t = 0 时刻的波形如题5-6图所示，则P 处质点的振动在t = 0时刻的旋转矢量图是［ ］[答案：A]5-7 一简谐波沿x 轴正方向传播，t = T /4时的波形曲线如题5-7图所示．若振动以余弦函数表示，且此题各点振动的初相取-π 到π 之间的值，则 ［ ］ (A) O 点的初相为00=φ(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ [答案：D]5-8 在驻波中，两个相邻波节间各质点的振动［ ］(A) 振幅相同，相位相同 (B) 振幅不同，相位相同 (C) 振幅相同，相位不同 (D) 振幅不同，相位不同 [答案：B]5-9 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：［ ］(A) 它的动能转化为势能. (B) 它的势能转化为动能.(C) 它从相邻的一段质元获得能量其能量逐渐增大. (D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小. [答案：D]ωS A O ′ωSA O ′ωωSAO ′(A)(B)(C)(D)S题5-6图5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是__________，波长是__________，频率是__________，波的传播速度是__________。

§ 9.2 平面简谐波的波动方程一、平面简谐波波动方程简谐波：如果波源和介质中的各质点都持续地作简谐振动，这种波称为简谐波。

平面简谐波：波面为平面的简谐波。

平面简谐波也称为一维简谐波，其表达式也称波函数(wave function)沿+x 方向传播的一维简谐波 (波速u ，振动角频率为ω)，假设媒质无吸收(质元振幅均为A )介质中任一质点（坐标为 x ）相对其平衡位置的位移（坐标为 y ）随时间的变化关系，即 称为波动方程。

设O 点处质点的振动方程为波线上坐标为x 的任意点P 处质点的振动方程振动从O 点传到P 点所需的时间为t 时刻点 P 的振动与 t-x/u 时刻点O 的振动状态相同，只是落后了Δt 点P 振动方程 式中称上式为沿x 轴正向传播的平面简谐波的波动方程(,)y x t cos O y A tω=(,)P y f x t ==？x t u∆=cos ()P xy A t uω=-2πων=u λν=xo任一点p参考点a波速u波方程的其它表示式讨论：（1）如果原点的初相位不为零设：点O振动方程则：波动方程为（2）如果平面简谐波沿x轴负方向传播则P点处质点相位比O点处质点的相位超前波动方程为二、波动方程的物理意义由从几方面讨论1 当x 一定时(设x =x0，即考察波线上某一点x0) 给出x =x0处质点的振动方程即x0处质元的振动表达式，表示x处的质点在各个不同的时刻位移随时间的变化情况，由它画出的曲线是x0处质元的振动曲线。

2 当t一定时(设t = t0，即在某一时刻t0)，给出t= t0时刻各质点的位移y分布情况反映t0时刻各不同x处质元的位移状况，即同一时刻x轴上各个质点离开它们平c o s2π()xy A tνλ=-[]c o sOy A tωϕ=+c o s[2π()]xy A tνϕλ=-+c o s[2π()]xy A tνϕλ=++c o s[2π()]xy A tνϕλ=-+()y y t=()y y x=c o s[2π()]xy A tνϕλ=-+2c o s()y A t xπωλ=-c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=++⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦衡位置的位移分布，由它画出的曲线即t 0时刻的波形曲线。

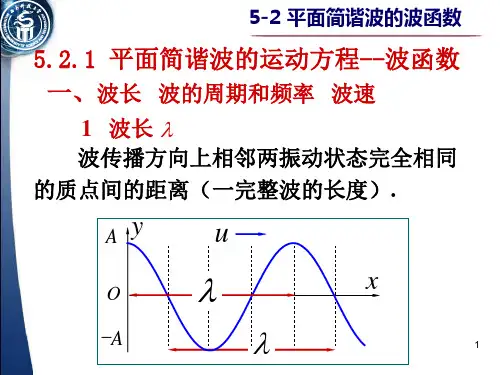
一、平面简谐波的概念平面简谐波是一种特殊的波动现象，它具有特定的波动方程和波动特性。

简谐波的振幅随时间以正弦或余弦函数变化，具有周期性和频率性，是物理学中常见的一种波动形式。

二、平面简谐波的波动方程1. 时间域的波动方程在时间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

2. 空间域的波动方程在空间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

3. 复数形式的波动方程在复数形式下，平面简谐波的波动方程可以表示为：\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的，都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。

它们之间通过变量的不同而具有不同的物理意义，但是描述的是同一种波动现象。

2. 复数形式的波动方程和实数形式的波动方程在复数形式下，简谐波的波动方程可以更加简洁地描述，通过复数的指数函数形式可以很方便地进行波动的运算和分析。

复数形式的波动方程和实数形式的波动方程是等价的，可以相互转化，但在不同的数学和物理背景下有着不同的应用优势。

四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式，广泛应用于物理学、工程学、生物学等领域。

它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值，可以用来描述和分析各种复杂的波动现象。