第十七届“华杯赛”成都赛区热身赛答案

5、甲、乙两轮船在静水中航行的速度分别为是 V 1, V 2,（V 1>V 2），下游的A 港与上游的B 港间的 水路路程为150千米。

若甲船从A 港，乙船从B 港同时出发相向航行，两船在途中的 C 点相遇。

若乙船从A 港，甲船从B 港同时出发相向航行，两船在途中 D 点相遇，已知C 、D 间的水路路程为 21千米。

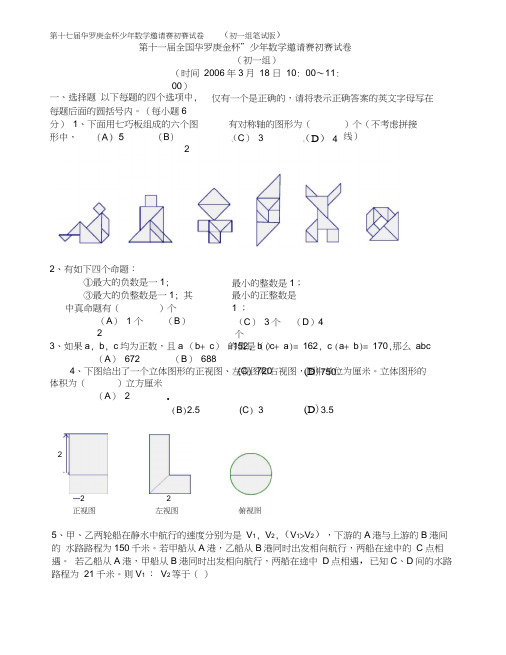
则V 1 ： V 2等于（ ）第十七届华罗庚金杯少年数学邀请赛初赛试卷 （初一组笔试版） 第十一届全国华罗庚金杯”少年数学邀请赛初赛试卷 （初一组） （时间 2006年3月 18 日 10: 00〜11:00） 仅有一个是正确的，请将表示正确答案的英文字母写在 有对称轴的图形为（ （C ） 3 ）个（不考虑拼接线） 一、选择题 以下每题的四个选项中, 每题后面的圆括号内。

（每小题6分） 1、下面用七巧板组成的六个图形中， 2 （D ） 4 2、有如下四个命题： ①最大的负数是一1; ③最大的负整数是一1; 其中真命题有（ ）个 （A ） 1 个 （B ） 2 最小的整数是1； 最小的正整数是1 ； （C ） 3个 （D ）4个 3、如果a , b , c 均为正数，且a （b + c ） 的值是（） （A ） 672 （B ） 688 4、下图给出了一个立体图形的正视图、左视图和右视图，图中单位为厘米。

立体图形的 体积为（ ）立方厘米 （A ） 2 O(B )2.5 =152, b (c + a )= 162, c (a + b )= 170,那么 abc (C ) 720 (D )750 (C ) 3 (D )3.5 2 —2正视图 2 左视图(初一组笔试版)59 里(C ) 45(D ) 4720042004, 20052005, 200於006。

大明从左往右依次计算前 a ,小光计算余下的1003个数的末位数字之和，并且记 (C )— 5 (D ) 5 二、A 组填空题(每小题8分)7、如图，以AB 为直径画一个大半圆。

第十五届华罗庚金杯少年数学邀请赛初赛试卷（小学组）一、选择题（每小题10分，满分60分。

以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。

）1．如图所示，平行四边形内有两个大小一样的正六边形，那么阴影部分的面积占平行四边形面积的（）。

2．两条纸带，较长的一条为23cm，较短的一条为15 cm。

把两条纸带剪下同样长的一段后，剩下的两条纸带中，要求较长的纸带的长度不少于较短的纸带长度的两倍，那么剪下的长度至少是（）cm。

（A）6 （B）7 （C）8 （D）93．两个水池内有金鱼若干条，数目相同。

亮亮和红红进行捞鱼比赛，第一个水池内的金鱼被捞完时，亮亮和红红所捞到的金鱼数目比是3：4；捞完第二个水池内的金鱼时，亮亮比第一次多捞33条，与红红捞到的金鱼数目比是5：3。

那么每个水池内有金鱼（）条。

（A）112 （B）168 （C）224 （D）3364．从中去掉两个数，使得剩下的三个数之和与最接近，去掉的两个数是（）。

5．恰有20个因数的最小自然数是（）。

（A）120 （B）240 （C）360 （D）4326．如图的大正方形格板是由81个1平方厘米的小正方形铺成，B，C是两个格点。

若请你在其它的格点中标出一点A，使得△ABC的面积恰等于3平方厘米，则这样的A点共有（）个。

（A）6 （B）5 （C）8 （D）107．算式的值为，则m+n 的值是 。

8．“低碳生活”从现在做起，从我做起。

据测算，1公顷落叶阔叶林每年可吸收二氧化碳14吨。

如果每台空调制冷温度在国家提倡的26℃基础上调到27℃，相应每年减排二氧化碳21千克。

某市仅此项减排就相当于25000公顷落叶阔叶林全年吸收的二气化碳；若每个家庭按3台空调计，该市家庭约有 万户。

（保留整数）9．从0、1、2、3、4、5、6、7、8、9这十个数字中，选出九个数字，组成一个两位数、一个三位数和一个四位数，使这三个数的和等于2010，那么其中未被选中的数字是 。

第十七届“华杯赛”决赛赛前强化训练（四年级）目录：一行程问题 (1)二智巧趣题、图形面积 (9)三较复杂的鸡兔和盈亏问题 (12)四排列、组合、抽屉 (16)五牛吃草问题 (19)一行程问题【例题精讲】例1．火车通过长为82米的铁桥用了22秒，如果火车的速度加快1倍，它通过162米铁桥就用16秒。

求火车原来的速度和它的长度？解：假设用原来的速度通过162米的铁桥，那么火车要用16×2＝32（秒）火车原来的速度为：(162－82)÷(32－22)＝8（米/秒）火车长为：8×22－82＝94（米）答：火车的速度是8米/秒，长度是94米。

例2．一条轮船往返于甲、乙两地之间，由甲至乙是顺水航行；由乙至甲是逆水航行。

已知船速是15千米/小时，逆水航行所用时间是顺水航行所用时间的2倍。

求水速？解：由题意可知，船行驶的路程相等。

而船顺水速度＝船速＋水速，逆水速度＝船速－水速。

方法一：因为逆水航行时间是顺水航行时间的2倍，但路程相同，说明顺水速度是逆水速度的2倍，而顺水速度＋逆水速度＝船速×2。

故顺水速度＋逆水速度＝15×2＝30(千米/时)。

根据和倍问题可知：逆水速度：30÷（2＋1）＝10（千米/时)，水速：15－10＝5（千米/时) 方法一：设水速为每小时x千米，由甲到乙顺水航行所用时间为a小时，由题意可列方程：（15＋x）×a＝（15－x）×2a解得：x＝5答：水流速度为每小时5千米。

例3．一只轮船从甲地开往乙地顺水而行，每小时行28千米，到乙地后，又逆水而行，回到甲地，逆水比顺水多行2小时，已知水速每小时4千米。

求甲乙两地相距多少千米？解：（1）逆水速度：28－4×2＝20(千米)；（2）逆水比顺水多用2小时航行的路程：20×2＝40(千米)；（3）顺水从甲地到乙地所用的时间：40÷(4×2)＝5(小时)；（4）甲乙两地相距多少千米：28×5＝140 (千米)。

第十七届华杯赛笔试公开题（北京中、高年级）捡分啦！北京赛区高年级组是单独命题的第十七届华杯赛小学高年级组笔试公开题甲、乙两人轮流从1～17这17个数中标记数．规定：（1）每次标记一个数；（2）不能标记已标记的数；（3）不能标记已标记数的2倍；（4）不能标记已标记数的二分之一；（5）谁没有数可标记谁就输．现在甲先标记了8，乙要保证自己必胜，乙接着应该标记__________．答案：先将数分组：1、2、4、8、163、6、125、107、149、11、13、15、17显然最后一组5个都能标，后两组各自只能标一个，第一组现在已经标8了，那么只有1、2可以标，两个中可以标1个，所以一共可以有5+1+1+1=8次，第二组，如果标3和12可标两次，标6只能标一次。

因为最后谁没有可标的谁就输，那么乙标完后就要剩下偶数次可标，所以乙标6，剩下8次可标，乙一定赢。

第十七届华杯赛小学中年级组笔试公开题北京时间16时, 小龙从镜子里看到挂在身后墙上的4块表, 如下图, 其中最接近16时的是（）.答案：北京赛区小学高年级组：乙应该接着标6小学中年级组：选D[ 此帖被宋倩倩老师在2012-03-15 09:39重新编辑]第十七届全国华罗庚金杯少年数学邀请赛公开题（小学高年级组笔试版）一个奇怪的动物庄园里住着猫和狗, 狗比猫多180只. 有20% 的狗错认为自己是猫；有20% 的猫错认为自己是狗. 在所有的猫和狗中, 有32% 认为自己是猫, 那么狗有（）只.（A）240 （B）248 （C）420 （D）842（x+x-180)*0.32=0.2X+0.8(x-180) 设狗为X只。

第十七届华杯赛笔试初赛将在本周六（2012.3.17日）开始考试了，现在华杯赛小学中、高年级组公开题和初一年级公开题已经公布了。

按以往的惯例，“华杯赛”网站在每届比赛开始前都要公布各参赛组笔试初赛各1道试题，让热爱数学的同学先睹为快，下面就是公布的试题，做做看，小编还给大家附带了参考答案哦！大家给点掌声吧！2012年第17届华杯赛笔试公开题及答案(中年级组)【试题】北京时间16时, 小龙从镜子里看到挂在身后墙上的4块表, 如下图, 其中最接近16时的是().答案：D2012年第17届华杯赛笔试公开题及答案(高年级组)【试题】一个奇怪的动物庄园里住着猫和狗, 狗比猫多180只. 有20% 的狗错认为自己是猫；有20% 的猫错认为自己是狗. 在所有的猫和狗中, 有32% 认为自己是猫, 那么狗有（）只.（A）240 （B）248 （C）420 （D）842答案：A方法1：方程法设猫有a只，其中认为自己猫的有80%a只，狗有b%只，其中认为自己是猫的有20%b只。

第十七届华罗庚金杯少年数学邀请赛初赛试卷（小学中年级组网络版）一、选择题（每小题10分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的括号内。

）1、如下图，时钟上的表针从（左）转到（右）最少经过了（）。

A、2小时30分B、2小时45分C、3小时30分D、3小时45分【解】B。

考查时间的加减问题。

一个是12：45，另一个是15：30，注意都使用24时制就很容易算出来。

15：30－12：45＝2：45。

2、在2012年，1月1日是星期日，并且（）。

A、1月份有5个星期三，2月份只有4个星期三B、1月份有5个星期三，2月份也有5个星期三C、1月份有4个星期三，2月份也有4个星期三D、1月份有4个星期三，2月份有5个星期三【解】D。

先算出1月有多少个星期三：一月是大月，有31天，31÷7＝4……3，说明有四个星期多3天，再从1月1日是星期日，余3，可以推算出1月31是星期二，因此1月份有4个星期三。

而2012年是闰年，2月有29天，由前面的分析可知1月31日是星期二，故2月1日是星期三，29÷7＝4……1，因此2月29日也是星期三，因此2月份有5个星期三。

3、有大小不同的4个数，从中任取3个数相加，所得到的和分别是180，197，208和222。

那么，第二小的数所在的和一定不是（）。

A、180B、197C、208D、222【解】C。

四个不同的数任取三个数相加，结果只有四种，用A，B，C，D分别代表由小到大的这四个数，容易组合出任取三个数相加按和从小到大的组合是：ABC、ABD、ACD、BCD，可以看出只有ACD组合中没有B，而且是第三大的和。

4、四百米比赛进入冲刺阶段，甲在乙前面30米，丙在丁后面60米，乙在丙前面20米。

这时，跑在最前面的两位同学相差（）米。

A、10B、20C、50D、60【解】A。

甲在乙前面30米，乙在丙前面20米，说明甲在丙前面50米，再加上丙在丁后面60米也就是丁在丙前面60米，不难看出丁在最前面，后面依次是甲、乙，最后是丙，丁与甲相差的距离是60－50＝10米，故选A。

2017华杯赛试题及答案2017华杯赛试题及答案１．摄制组从A市到B市有一天的路程，计划上午比下午多走100千米到C市吃午饭，由于堵车，中午才赶到一个小镇，只行驶了原计划的三分之一，过了小镇，汽车赶了400千米，傍晚才停下来休息，司机说，再走从C市到这里路程的三分之一就到达目的地了.问:A、B 两市相距多少千米？2．问：（a）1995年全年有几个星期日？全年有几个月有五个星期日？（b）1996年全年有几个星期日？全年有几个月有五个星期日？3．甲、乙、丙三个班人数相同，在班之间举行象棋比赛，将各班同学都按1，2，3，，编号．当两个班比赛时，具有相同编号的同学在同一台对垒，在甲、乙两班比赛时，有15台是男、女生对垒；在乙、丙两班比赛时，有9台是男、女生对垒．试说明在甲、丙两班比赛时，男、女生对垒的台数不会超过24．什么情况下，正好是24？4．用0，1，2，3，4五个数字，组成四位数，每个四位数中的数字不同（如1023，2341），求全体这样的四位数之和．5．某幼儿园的小班人数最少，中班有27人，大班比小班多6人，春节分橘子25箱，每箱橘子不超过60个，不少于50个，橘子总数的个位数是7，若每人分19 个，则橘子数不够，现在大班每人比中班每人多分一个，中班每人比小班每人多分一个，刚好分完，问这时大班每人分多少橘子？小班有多少人？6．一个圆周上有12个点，，，，．以它们为顶点连三角形，使每个点恰是一个三角形的顶点，且各个三角形的边都不相交．问有多少种连法？参考答案1．A，B两市相距600千米 2．（a）1995年共有53个星期日，全年有五个月有五个星期日，（b）1996年共有52个星期日，全年只有四个月有五个星期日． 3．略 4．259980 5．大班每人分得18个橘子；小班有25人． 6．共有55种不同的连法1.【解】如图所示．设小镇为D点，傍晚到达E点，F为AB中点.AD是AC的三分之一，即DC＝2×AD，EB是CE的二分之一，即CE＝2×EB，所以DE＝DC＋CE＝2×(AD十EB)已知DE＝400，所以AD＋EB＝400÷2＝200，从而AB＝400＋200＝600(千米)答：A、B两市相距600千米【注】本题中，“计划上午比下午多走100千米”这一条件是多余的2.【解】(a)1995年1月1日是星期日，1995年全年有365天，每7天有且仅有一个星期日7×52＝364，因此，从1995年1 11 2日到1995年12月31日．这364天中有52个星期日，加上1995年1月1日这个星期日，共是53个星期日.最小的月有28天，最大的月有31天，因此无论哪个月都最少有4个星期日，最多有5个星期日.53＝12×4＋5，因此，1995年中有五个月有五个星期日.(b)1995年1月1日是星期日，经过364天后，1995年12月31日也是星期日.所以1996年1月1日是星期一.1996年是闰年，2月有29天，经过364天后，1996年12月30日是星期一，所以1996年全年共有52个星期日，全年只有四个月有五个星期日.3.【解】我们可以把乙班同学分成三部分，第一部分为与甲班相同编号的同学异性者（由题设可知这部分乙班同学为15人），第二部分为与丙班相同编号的同学异性者（由题设可知这部分乙班同学为9人），其余为第三部分.设A同学属于第三部分，他与甲班相同编号的同学通性，与丙班相同编号的同学也为同性，所以，与A相同编号的甲班和丙班同学必为同性.由此可知，甲、丙两班比赛时，男、女生对垒的台数不会超过24.只有当与乙班第一部分相同编号的丙班同学均与乙班同学同性，并且与乙班第二部分相同编号的甲班同学也均与乙班同学同性时，甲、丙两班比赛中，男、女生对垒的台数正好是24.4.【解】千位数字是1的有4×3×2＝24个(因为百位数字可从0、2、3、4中选择，有4种，百位确定后，十位有3种选择，百位，十位确定后，个位有2种选择)．千位数字是2、3、4的也有24种。

一、选择题1、计算：[(0.8 1) 24] 9 7.6 (___) 5 14（A）30 （B） 40 （C）50 （D）60 【答案】 B【解析】原式 =[(0.8+0.2) 24+6.6] 147.6 930.6 147.6 93.4 14 7.6 47.6 7.6 402、以平面上 4 个点为端点连接线段，形成的图形中最多可以有（（A）3（B）4）个三角形。

（C）6（D）8【答案】 D【解析】几何计数注意看清题目，是以 4 个点为端点连接线段，构成的图形最多可以有多少个三角形；而不是以这可以有多少三角形，所以如图可知，有8个。

选 D4 个点位端点，最多3、一个奇怪的动物庄园里住着猫和狗,狗比猫多180只.有20%的狗错认为自己是猫；在所有的猫和狗中,有32%认为自己是猫,那么狗有（）只.（ A） 240（B）248（C）420（D）842有 20% 的猫错认为自己是狗.【答案】 A【解析】这是一道典型的比例应用题。

方法一、方程法这个是最直接最快的。

假设狗有 x 只，有：x 20% ( x 180) 80% (x x 180) 32% ；1 x 4(x 180)8(2 x 180)5 5 25(两边同乘以 25)5x+20( x 180) 8(2x180)25x 3600 16x 14409x 2160x 240所以狗的数量就是240 只。

（也可以假设猫为x 只，这样计算值会小很多。

）方法二、存在比例的题目都可以考虑十字交叉来做：由以上可以发现狗和猫的数量之比是4:1 ；相差 3 份，相差 180 只，即 1 份为 60 只。

狗是 4 份，所以狗是240 只。

（对于太原的同学来说，十字交叉可能不太好理解，这是学而思六年级秋季班的内容，十字交叉式一种技巧。

）4、老师在黑板上写了从 1 开始的若干个连续自然数，1,2,3 ，后来擦掉其中一个数，剩下数的平均数是25 11，24擦掉的自然数是（）A、 12B、 17C、 20D、 3【答案】 D【解析】1，2，3，...一直到n的平均数可以表示为1+n2现在擦掉一个数之后，剩下的数，平均值为25 11，估算有1+n=25 ，n 的值在50 左右。

历届华杯赛决赛试题剖析5华罗庚金杯少年数学邀请赛决赛试题（小学组）真题尝试感悟心得＞填空题（每小题10分，共80分）1.算式10 —10.5十［5.2x14.6 —（9.2x5.2 + 5.4x3.7 —4.6xl.5）］的值为_______ ・2.箱了里已有若干个红球和黑球，放入一些黑球后，红球占全部球数的四分再放入一些红球后，红球的数量是黑球的三分Z二.若放入的黑球和红球数量相同，则原来箱子里的红球与黑球数量之比为_______ ・3.有两个休积之比为5:8的圆柱，它们的侧面的展开图为相同的长方形,如果把该长方形的长和宽同时增加6,其面积增加了114.那么这个长方形的面积为__________________ ・4.甲、乙两个粮库原來各存冇整袋的粮食，如果从甲粮库调90袋到乙粮库，则乙粮库存粮的袋数是甲粮库的2倍•如果从乙粮库调若干袋到卬粮库，则卬粮库存粮的袋数是乙粮库的6倍.那么甲粮库原来最少存有袋的粮食.5.现有211名同学和四种不同的巧克力，每种巧克力的数量都超过633颗.规定每名同学最多拿三颗巧克力，也可以不拿.若按照所拿巧克力的种类和数量都是否相同分组，则人数最多的一组至少有 _____________名同学.6.张兵1953年出生，在今年之前的某一年，他的年龄是9的倍数并且是这一年的各位数字z和，那么这一年他_________________________________________________岁.右图是一个五棱柱的平而展开图，图屮的正方形边长都为2.按图所示数据，这个五棱柱的体积等于________ .8＞在乘法算式章绿X花红了二春光明媚中，汉字代表非零数字，不同汉字代表不同的数字，那么春光明媚所代表的四位数最小是 _________ ・二、解答下列各题（每题10分，共40分，要求写出简要过程）如右图，ABCD是平行四边形，E为AB延长线9.上一点，K为延长线上一点.连接BK,DE相交于一点O.问: 四边形ABOD与四边形ECKO的面积是否相等？请说明理由.10.能否用500个右图所示的1x2的小长方形拼成一个5x200的大长方形，使得5x200的长方形的每一行、每一列都有偶数个星？请说明理由.11.将一个In位数的前农位数和后z?位数各当成一个/?位数，如果这两个〃位数Z和的平方止好等于这个加位数，则称这个加位数为卡布列克（Kabulek）怪数，例如，（30 + 25）2 =3025，所以3025是一个卡布列克怪数.请问在四位数中有哪些卡布列克怪数？12.已知98个互不相同的质数P1，#2,…,P98，记N = p； + p； + ・・・ + P；,问:N被3除的余数是多少？三、解答下列各题（每小题15分，共30分，要求写出详细过程）13.小李和小张在一个圆形跑道上匀速跑步，两人同时同地岀发，小李顺时针跑，每72秒跑一圈；小张逆时针跑，每80秒跑一圈.在跑道上划定以起点为中心的丄岡弧区间，那么两人同时在划定的区间内所持续的4时间为多少秒？14.把一个棱长均为整数的长方休的表面都涂上红色，然后切割成棱长为1的小立方块，其中，两而冇红色的小立方块冇40块，一而冇红色的小立方块有66块，那么这个长方体的体枳是多少？第十七届华罗庚金杯少年数学邀请赛决赛笔试试题A参考答案（小学高年级组）一、填空（每题10分，共80分）题号12345678答案9.31:24015371874396二、解答下列各题（每题10分，共40分，要求写出简要过程）9.答案：是.解答.连接AC.则° ECKB ~ °ACEB丁O'BCKQ \CEB丁Q'BCAV - V °MCE所以_ °^EADS ECKB _ S^BE因此S ECKO =S ABOD・即四边形ABOD的而积二四边形ECKO的而积.10.答案：能解答.首先构造5x4的长方形如下：令令令令令令然示用5()个5 x 4的即可拼成5 x 200的长方形.11.答案：2025,3025,9801.解答.设一个四位卡布列克怪数为100x + y,其中10SxS99,0SyS99•则由题意知100x4- y = (x+ y)2,两边模99 得兀 + y = (x + y)2 (mod 99),因此99 l(x+y)(x + y -1),故x + yLx + y -1中有一个能被9整除，也有一个能被11整除(可能是同一个数),且有102 <(x+y)2= 100x +y<1002,即10<x+y<100. (*)若x + y能被99整除，由(*)知兀+y只能是99,满足条件的四位数是9801；若x + y—1 能被99整除，由(*),显然没冇满足条件的四位数；此外，可设x + y =9/n, x + y—1 = \\n,则有9/n-l 由(*)，加和n均为小于12的正整数，故得到加=5, n=4, x+y 只能是45,满足条件的四位数是2025；反Z,可设兀+歹一1=9加，x+y =lln,满足条件的四位数是3025.故四位数中冇三个卡布列克怪数，它们分别为2025, 3025和9801.12.答案：1或2解答.对于质数3, 32被3整除.其余的质数，要么是3£ + 1型的数，要么是3£ + 2型的数. 由于(3R+1)2 =9R+6R + l = 3(3/+2 幻+ 1,被3除余1,且(3k + 2)2 =9疋+12^ + 4 = 3(3疋+4鸟 + 1) + 1,被3除也余1.因此有(1)若这98个质数包含3吋,N被3除的余数等于97被3除的余数，等于1.(2)若这98个质数不包含3时,N被3除的余数等于98被3除的余数，等于2.三、解答下列各题(每题15分，共30分，要求写岀详细过程)13.答案：3,9,11,18解答.设起跑时间为0秒时刻，则小李和小张在划定区间跑的时间段分别为[0,9], [72k — 9,72R + 9], 1,2,3,…，和[0,10], [80/77 -10,80/n + 10], m = 1,2,3, • • • •其中创表示笫a秒时刻至笫b秒时刻.显然[0,9]即前9秒里两类时间段的公共部分. 此外，考虑[72—9,7219]和[80加一10,80加+ 10]的公共区间，加为正整数,分两种情况:1)12k = 80/n,即小李和小张分别跑了k圈和加圈同时回到起点，他们二人同时在划定区域跑了18秒.2)12k80m,例如72上-9 72上+9I 1I i80^ -10 80^3 4-1012k-9 < 80m-10<72)t+9< 80/T? +10 o 1 5 80/n - 72k <19 ①.两人同时在划定区域内跑了72k +9-(80m-10) = 19 —(8(加—72灯.由①知80加-72£=8, 16.于是两人同时在划定区域内跑持续时间为11秒或3秒.其它情况类似可得同样结來.综上,答案为3,9,11,18.14・答案：150解答.设立方体的长，宽，高分别为乙”,其屮xSySz,且为整数.注意，两血有红色的小立方块只能在长方体的棱上岀现.如果兀= l,y = l,则没有两面为红色的立方块，不符合题意.如果x = l,y>l,则没有只有一面为红色的立方块，不符合题意.因此x>2•此时两面出现红色的方块只能与长方体的棱共棱.一面出现红色的方块只与立方体的面共面.有下血的式子成立4x[(x_2) + (y_2) + (z — 2)] = 40, (1)2 x [(x — 2)(y _ 2) + (兀-2)(z - 2) + (y — 2)(z — 2)] = 66. (2)由(1)得到兀+y + z = 16, (3)由(2)得到小 + 疋+yz = 85. (4)由(3)和(4)可得，扌+于+才=86,这样lSx,y,z59.由(4)得到(x + y)(兀 + z) = 85 -t- %2. (5)若兀=2，则由(5)得到(2 + y)(2 + z) = 85 + 4 = 89 = lx89, 的取值不能满足(3).若兀=3，贝ij由(5)得到(3 + y)(3 + z) = 85 + 9 = 94 = 2x47, y,z的取值不能满足(3).若兀=4,则由(5)得到(4+y)(4 + z) = 85 + 16 = 101 = 1x101, 的取值不能满足(3).当兀=5 时，山(5)得至i」(5 + y)(5 + z) = 85 + 25 = 110 = 2x5xll,此吋〉，= 5,z = 6满足条件.如果兀»6,贝'Jx + y + z > 18,与(3)矛盾.综上x = 5,y = 5,z = 6是问题的解，这是长方体的体积为15().。

第十七届华杯赛笔试公开题（北京中、高年级）捡分啦！北京赛区高年级组是单独命题的第十七届华杯赛小学高年级组笔试公开题甲、乙两人轮流从1～17这17个数中标记数．规定：（1）每次标记一个数；（2）不能标记已标记的数；（3）不能标记已标记数的2倍；（4）不能标记已标记数的二分之一；（5）谁没有数可标记谁就输．现在甲先标记了8，乙要保证自己必胜，乙接着应该标记__________．答案：先将数分组：1、2、4、8、163、6、125、107、149、11、13、15、17显然最后一组5个都能标，后两组各自只能标一个，第一组现在已经标8了，那么只有1、2可以标，两个中可以标1个，所以一共可以有5+1+1+1=8次，第二组，如果标3和12可标两次，标6只能标一次。

因为最后谁没有可标的谁就输，那么乙标完后就要剩下偶数次可标，所以乙标6，剩下8次可标，乙一定赢。

第十七届华杯赛小学中年级组笔试公开题北京时间16时, 小龙从镜子里看到挂在身后墙上的4块表, 如下图, 其中最接近16时的是（）.答案：北京赛区小学高年级组：乙应该接着标6小学中年级组：选D[ 此帖被宋倩倩老师在2012-03-15 09:39重新编辑]第十七届全国华罗庚金杯少年数学邀请赛公开题（小学高年级组笔试版）一个奇怪的动物庄园里住着猫和狗, 狗比猫多180只. 有20% 的狗错认为自己是猫；有20% 的猫错认为自己是狗. 在所有的猫和狗中, 有32% 认为自己是猫, 那么狗有（）只.（A）240 （B）248 （C）420 （D）842（x+x-180)*0.32=0.2X+0.8(x-180) 设狗为X只。

第十七届华杯赛笔试初赛将在本周六（2012.3.17日）开始考试了，现在华杯赛小学中、高年级组公开题和初一年级公开题已经公布了。

按以往的惯例，“华杯赛”网站在每届比赛开始前都要公布各参赛组笔试初赛各1道试题，让热爱数学的同学先睹为快，下面就是公布的试题，做做看，小编还给大家附带了参考答案哦！大家给点掌声吧！2012年第17届华杯赛笔试公开题及答案(中年级组)【试题】北京时间16时, 小龙从镜子里看到挂在身后墙上的4块表, 如下图, 其中最接近16时的是().答案：D2012年第17届华杯赛笔试公开题及答案(高年级组)【试题】一个奇怪的动物庄园里住着猫和狗, 狗比猫多180只. 有20% 的狗错认为自己是猫；有20% 的猫错认为自己是狗. 在所有的猫和狗中, 有32% 认为自己是猫, 那么狗有（）只.（A）240 （B）248 （C）420 （D）842答案：A方法1：方程法设猫有a只，其中认为自己猫的有80%a只，狗有b%只，其中认为自己是猫的有20%b只。