截面与三视图(一)(人教版)word版

1.截面可能是圆的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥2.截面可能是三角形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥3.截面可能是矩形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥4.截面可能是梯形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥5.截面可能是平行四边形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥6.用一个平面截下面的几何体，截面不可能是三角形的是_______A 圆锥B圆柱C长方体 D 六棱柱7. 正方体的截面不可能是________A 三角形B 四边形C 五边形D 六边形E 七边形8. 基本几何体的三视图(主视图反映物体的长和高，俯视图是长和宽，左视图是高和宽）几何体主视图左视图俯视图圆柱圆锥四棱锥空心圆柱9.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示，则搭成这个几何体的小正方体的个数最多为___,最少为____。

___．10. 如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则小立方体的个数不可能是( )A．6个B．7个C．8个D．9个11. 如图是由若干个大小相同的正方体搭成的几何体 的三视图，则该几何体所用的正方形的个数是________12.由一些完全相同的小正方体搭成的几何体的主视图和左视图 如图所示，则组成这个几何体的小正方体的个数可能是13. 几个棱长为1的正方体组成的几何体的 三视图如图所示，则这个几何体的体积是＿＿＿＿14．几个立方块所搭几何体的俯视图如图所示，小正方形的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.15.下图，该几何体是_______. 16. 下图，则这个几何体是______17. 下图，该几何体是_______. 18. 下图,三视图表示的几何体是________19.主视图、俯视图和左视图都是．．长方形的几何体是_________(填一个即可) 20. 三视图都相同的几何体可能是_________、____________.(有两种类型)3 2 1 1 2 24 1 3主视图左视图2 2 1 3421.下列四个水平放置的几何体中，三视图如图所示的是( )A．B．C．D22.中央电视台有一个非常受欢迎的娱乐节目：墙来了！选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞，则该几何体为( )A．B．C．D．23.如图所示，下列水平放置的几何体中，俯视图是矩形的是( )A．B．C．D．24. 下列四个几何体中，主视图是三角形的是( )A．B．C．D．25. 下列几何体中，俯视图相同的是( )A①② B①③C②③ D ②④26.下面四个几何体中，左视图是四边形的几何体共有 ( )A 1 个B 2个C 3个D 4个27.下列四个几何体中，主视图与左视图相同的几何体有( )A.1个B.2个C.3个D.4个28.球和圆柱在水平面上紧靠在一起，组成如图所示的几何体，托尼画出了它的三视图，其中他画的俯视图应该是( )A．两个相交的圆B．两个内切的圆C．两个外切的圆D．两个外离的圆29.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是( )。

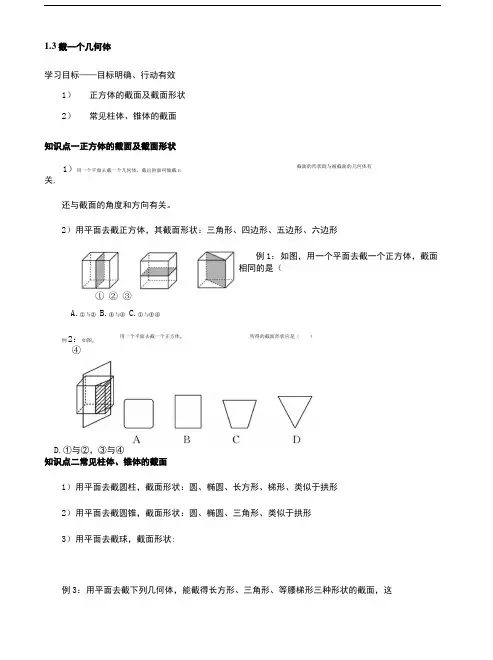
1）用一个平面去截一个几何体，截出的面叫做截H 截面的形状既与被截面的几何体有例2：如图, 用一个平面去截一个正方体, 所得的截面形状应是（）1.3截一个几何体学习目标——目标明确、行动有效1）正方体的截面及截面形状2）常见柱体、锥体的截面知识点一正方体的截面及截面形状关,还与截面的角度和方向有关。

2）用平面去截正方体，其截面形状：三角形、四边形、五边形、六边形例1：如图，用一个平面去截一个正方体，截面相同的是（④D.①与②，③与④知识点二常见柱体、锥体的截面1）用平面去截圆柱，截面形状：圆、椭圆、长方形、梯形、类似于拱形2）用平面去截圆锥，截面形状：圆、椭圆、三角形、类似于拱形3）用平面去截球，截面形状:例3：用平面去截下列几何体，能截得长方形、三角形、等腰梯形三种形状的截面，这① ② ③A.①与②B.③与④C.①与③④2个3个4个5个个几何体是（例4：用一个平面去截下列六个几何体，能得到长方形截面的几何体有（例5：用平面去截下列几何体，截面的形状不可能是圆的几何体是（ ）A.球B.圆锥C.圆柱D.正方体例6： —个几何体的一个截面是三角形，则原几何体一定不是下列图形中的（ ）A.圆柱和圆锥B.球体和圆锥C.球体和圆柱D.正方体和圆锥巩固练习1. 下列关于截面的说法正确的是（ ）A.截面是一个平面图形B.截面的形状与所截几何体无关C.同一个几何体，截面只有一个D.同一个几何体，截面的形状都相同 2. 用一个平面截去正方体的一个角，则截面不可能是（ ）A.锐角三角形B.等腰三角形C.等腰直角三角形D.等边三角形3. 如图①，大正方体上截去一个小正方体后，可得到图②的几何体.设原大正方体的表 面积为S,图②中几何体的表面积为S\那么S ，与S 的大小关系是（理色 图①图②A. S F>S B. S ，=S C. S ，VS D.不能确定 4.有一个圆锥体，用一个平面从不同的位置去截它，如图①〜④，能得到不同的截面，正确的有（）A. 1种B. 2种C. 3种D. 4种1.4从三个方向看物体的形状学习目标——目标明确、行动有效1）组合体的视图可转化为基本几何体的视图，然后根据位置关系确定组合体的视图.知识点一画出从三个方向看到几何体的图形例1.如图是由6个大小相同的正方体组成的几何体，它的左视图是（）例2.下列几何体中，有一个几何体的俯视图的形状与其他三个不一样，这个几何体是（））平方厘米。

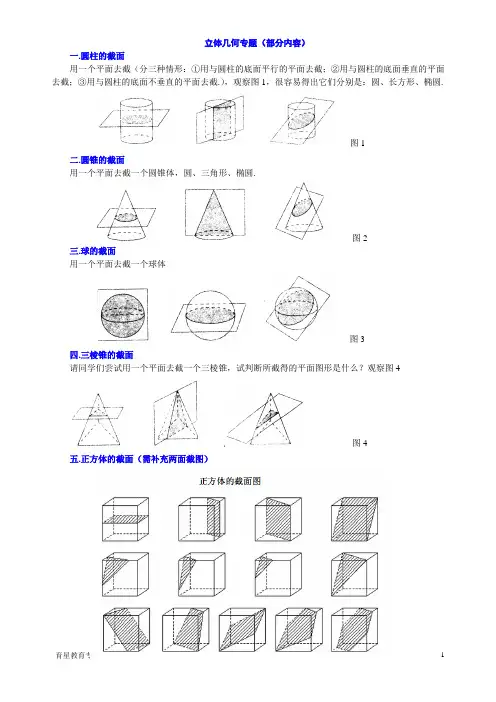
立体几何专题（部分内容）一.圆柱的截面用一个平面去截（分三种情形：①用与圆柱的底面平行的平面去截；②用与圆柱的底面垂直的平面去截；③用与圆柱的底面不垂直的平面去截.），观察图1，很容易得出它们分别是：圆、长方形、椭圆.图1二.圆锥的截面用一个平面去截一个圆锥体，圆、三角形、椭圆.图2三.球的截面用一个平面去截一个球体图3四.三棱锥的截面请同学们尝试用一个平面去截一个三棱锥，试判断所截得的平面图形是什么？观察图4图4五.正方体的截面（需补充两面截图）补充：三视图或投影经典考题公式：空间几何体的表面积棱柱、棱锥的表面积：各个面面积之和圆柱的表面积 ：222S rl r ππ=+ 圆锥的表面积：2Srl r ππ=+圆台的表面积：22S rl r Rl R ππππ=+++球的表面积：24SR π=扇形的面积公式2211=36022n R S lr r πα==扇形（其中l 表示弧长，r 表示半径，α表示弧度） 空间几何体的体积 柱体的体积 ：VS h =⨯底锥体的体积 ：13V S h =⨯底 台体的体积 ： 1)3V S S S S h =++⨯下下上上（ 球体的体积：343V R π=空间几何体的三视图和直观图：正俯长相等、正侧高相同、俯侧宽一样正视图：光线从几何体的前面向后面正投影，得到的投影图。

侧视图：光线从几何体的左边向右边正投影，得到的投影图。

俯视图：光线从几何体的上面向右边正投影，得到的投影图。

1、线线平行的判断：（1）、平行于同一直线的两直线平行。

（3）、如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

（6）、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（12）、垂直于同一平面的两直线平行。

2、线线垂直的判断：（7）、在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

（8）、在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。

第二讲截面与三视图（一）截一个几何体截面：用一个平面去截一个几何体，截出的面叫做截面。

（1）用一个截面去截长方体或正方体，截面可能是等腰三角形、等边三角形、但不可能是三角形，也可能是正方形，长方形，梯形，五边形等，最多可截得边形。

可能出现：锐角三角形，等边、等腰三角形；正方形，长方形，平行四边形，菱形，不等腰梯形，等腰梯形；五边形；六边形，正六边形。

不可能出现：钝角、直角三角形，直角梯形，正五边形，七边形或更多变形（2）用一个截面去截圆柱，截面可能是正方形，长方形，圆或椭圆。

（3）用一个截面去截圆锥，截面可能是等腰三角、圆、抛物线形或椭圆。

（4）三棱锥的截面可以是三角形、长方形、四边形。

其中四边形可以是特殊的矩形、梯形。

截面的形状多为圆和多边形，也可能是不规则图形，一般与下面两点有关：（1）几何体的形状；（2）切截的方向和角度一般的，截面与几何体的几个面相交，就得到几条交线，截面与平面相交就得到几边形;截面与曲面相交，得到曲线，截面是圆或不规则图形。

（二）从三个不同方向观察物体我们从不同方向观察物体时，从正面看到的图形叫做主视图，从左边看到的图形叫做左视图，从上面看到的视图叫做俯视图。

典型例题讲解：例1.用一个平面去截圆锥，截面图形不可能是（）A．B．C．D．例2.把正方体的八个角切去一个角后，余下的图形有（）条棱．A．12或15B．12或13C．13或14D．12或13或14或15例3.如图所示的正方体，用一个平面截去它的一个角，则截面不可能是（A．锐角三角形B．等腰三角形C．等腰直角三角形D．等边三角形例4.如图，由三个小立方体搭成的几何体的俯视图是（）A．B．C．D．例5.如图是某几何体的三视图，其侧面积（）A．6B．4πC．6πD．12π例6.如图是几个相同的小正方体搭成的几何体的两种视图，则搭成这个几何体的小正方体的个数是（）A．7B．6C．5D．4例7.如图所示，几何体是由一些大小相同的小正方体组成，其三视图中面积最小的是（）A．主视图B．左视图C．俯视图D．都一样例8.如图是一个由相同小正方体搭成的几何体俯视图，小正方形中的数字表示在该位置上的小正方体的个数，则这个几何体的主视图是（）A．B．C．D．随堂练习：1（易）．一个平面截圆柱，则截面形状不可能是（）A．圆B．三角形C．长方形D．梯形2（易）．给出以下四个几何体，其中不能截出圆的几何体是（）A．球B．圆锥C．正方体D．圆柱3（易）．用平面去截下列几何体，不能截出三角形的是（）A．B．C．D．4（易）．用平面去截如图所示的三棱柱，截面形状不可能是（）A．三角形B．四边形C．五边形D．六边形5（易）．用一个平面分别去截：①球；①四棱柱；①圆锥；①圆柱；①正方体．截面可能是三角形的有（）A．4个B．3个C．2个D．1个6（易）．用一个平面去截一个几何体，不能截得三角形截面的几何体是（）A．圆柱B．圆锥C．三棱柱D．正方体7（易）．用平面去截下列几何体，截面的形状不可能是圆的几何体是（）A．球B．圆锥C．圆柱D．正方体8（易）.如图所示的几何体的主视图是（）A．B．C．D．9（易）．如图是一个几何体的三视图，则这个几何体的全面积是（）A．14πB．24πC．26πD．36π10（中）.下图是由大小一样的小正方块摆成的立体图形的三视图，它共用多少个小正方块摆成（）A．5B．8C．7D．611（中）．由一些完全相同的小立方块搭成的几何体的主视图、俯视图如图所示，那么搭成这个几何体最少用的小立方块的个数是（）A．8B．7C．6D．512（中）．某物体的展开图如图，它的左视图为（）A．B．C．D．13（难）．如图，是一个几何体的三视图，根据图中标注的数据可求得这个几何体的体积为（）A．24πB．32πC．36πD．48π14（难）．如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（）A．320cm B．395.24cm C．431.77cm D．480cm15（中）．在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（）A．9箱B．10箱C．11箱D．12箱16（中）．用若干个小立方块搭一个几何体，使得它的左视图和俯视图如图所示，则所搭成的几何体中小立方块最多有（）A．15个B．14个C．13个D．12个17（难）．一个几何体是由一些大小相同的小正方块摆成的，其主视图与俯视图如图所示，则组成这个几何体的小正方块最多有（）A．7个B．6个C．5个D．4个18（难）．若干桶方便面摆放在桌子上，如图所示是它的三视图，则这一堆方便面共有（）A．6桶B．7桶C．8桶D．9桶19（难）如图①是圆柱被一个平面斜切后得到的几何体，请类比梯形面积公式的推导方法（如图①），推导图①几何体的体积为．（结果保留π）。