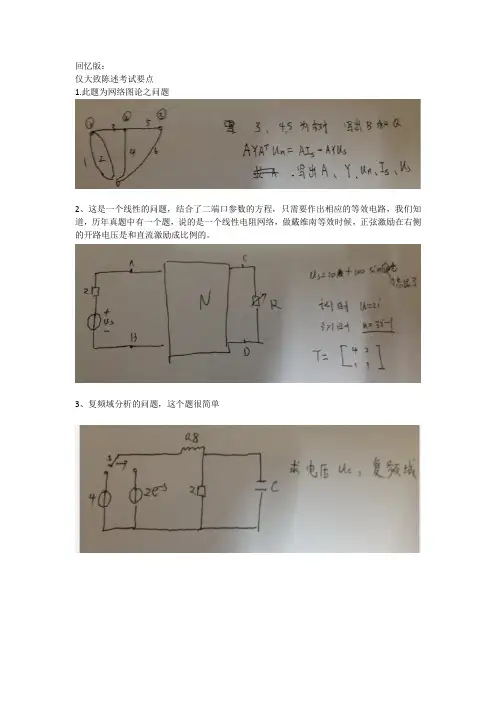
2013年清华大学电路原理考研真题
- 格式:doc
- 大小:17.00 KB
- 文档页数:2


清华大学硕士电路原理-7(总分:99.99,做题时间:90分钟)一、解答题(总题数:10,分数:100.00)1.下图所示电路中,当开关S闭合时,3个电流表的读数均为1A。
求开关S打开时,电流表A 1的读数。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解当S闭合时,3个电流表的读数为当S打开时,电流表A 1的读数为2.下图所示电路为一三相电路,电源为对称三相电源。
开关S闭合时,3个电流表的读数均为5A。
求开关S打开后3个电流表的读数。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解当开关S闭合时,电路为对称三相电路,3个电流表中的电流均为线电流,此时每相负载中的相电流为开关S打开后,一相负载断路,其余两相负载两端的电压不变,其中的电流也不变,所以,电流表A 2的读数仍为5A。
而A 1、A 2中的电流相当于对称运行时的相电流,即此时A 1、A 3的读数为2.89A。
3.三相对称电路如下图所示,测得功率表W 1的读数为2840W,W 2的读数为1204W,电流表A的读数为7.5A,求负载参数R和L(设电源频率f=50Hz)。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解两块功率表的读数是三相电路吸收的总功率,即电阻消耗的功率。
设△形连接负载中每相负载流过的电流为I ab,每相负载的阻抗角为φ。

清华大学硕士电路原理-20(总分:100.00,做题时间:90分钟)一、解答题(总题数:11,分数:100.00)1.试将戴维南定理推广,导出由线性电阻和独立电源组成的有源双口网络的最简单的等效电路,说明怎样通过测量外部的电压、电流来确定等效电路中的元件数值。
将所得结果用于下图所示的双口网络,求出它的最简单的等效电路。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解对含独立电源的一端口网络,根据戴维南定理可等效为电压源和电阻串联电路(图(a)所示电路)。
(a)其电压、电流关系为U=R i I+U o,U o为含独立电源一端口网络的开路电压。
对含独立电源的二端口网络(图(b)所示电路),可得类似的矩阵形式关系式:(b)其等效电路如图(c)或图(d)所示。
(c)(d)其中,R 1、R 2、R 3为对应无源二端口的T型等效电路中的参数;R a、R b、R c为对应无源二端口的Ⅱ型等效电路中的参数。
U o1、U o2为含源二端口两个端口开路时的端口电压。
应用上述结果计算上图所示二端口的T型等效电路(如图(d)所示)或Ⅱ型等效电路(如图(d)所示)的参数,所得结果如下:2.下图所示电路中,二端口网络N的传输参势求负载电阻R 2为何值时其上获得最大功率?并求此最大功率。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解利用两个二端口的级联,原电路可等效为图(a)所示电路。
(a)其中二端口网络N"传输参数矩阵其传输参数方程为求戴维南等效电路(图(b)所示电路):开路电压为I 2 =0时的电压U 2,即(b)等效电阻为独立源置零时,端口2的入端电阻当R 2 =R i =4.33Ω时获得最大功率,此最大功率为3.已知下图(a)中二端口N的传输参数为R为非线性电阻,其伏安特性如图(b)所示。


清华大学硕士电路原理-15(总分:100.00,做题时间:90分钟)一、解答题(总题数:10,分数:100.00)1.求下列函数f(t)的象函数。
(1)f(t)=1+2t+3e -4t(2)f(t)=3te -5t(3)f(t)如下图所示。
(分数:10.00)__________________________________________________________________________________________ 正确答案:()解析:解已知原函数f(t),求其象函数F(s)可利用拉普拉斯正变换(以下简称拉氏变换)的定义式,或直接利用常用函数的拉普拉斯变换式及变换的性质。
用定义求象函数较繁,而一般给定的原函数是常用函数,可利用变换结果和一些变换的性质直接求象函数。
(1)直接利用常用函数的拉氏变换结果得(2)直接利用常用函数的拉氏变换结果得(3)先由题目中的图写出函数的时域表达式为f(t)=t[ε(t)-ε(t-1)]+[ε(t-1)-ε(t-2)]=tε(t)-(t-1)ε(t-1)-ε(t-2)利用常用函数的拉氏变换结果和时域的平移性质得其象函数为(1).求函数f(t)=1+2e -4t +3te -5t的象函数。
(分数:5.00)__________________________________________________________________________________________ 正确答案:()解析:解(2).函数f(t)为e -t在0~2s之间的波形,如下图所示,求f(t)的象函数。
(分数:5.00)__________________________________________________________________________________________ 正确答案:()解析:解由题目中的图写出函数f(t)的时域表达式为f(t)=e -t [ε(t)-ε(t-2)]=e -tε(t)-e -2 e -(t-2)ε(t-2)则其象函数为2.已知下列象函数F(s),求原函数f(t)。

清华大学硕士电路原理-9(总分:100.01,做题时间:90分钟)一、解答题(总题数:13,分数:100.00)1.已知一电路两端的电压为u(t)=(1+2sinωt+cos3ωt)V,流过的电流为i(t)=[1+sin(ωt+60°)+cos3(ωt-30°)]A,且知电压、电流取关联的参考方向。
求这个电路消耗的有功功率。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解根据非正弦周期电流电路平均功率的求法,该电路吸收的平均功率为P=U 0 I 0 +U 1 I 1 cosφ1 +U 3 I 3 cosφ3=1.5W2.已知题图(a)所示的互感电路中,原边线圈中有电流i,i的波形如题图(b)所示。
互感线圈的副边是开路的。
试定性画出该电路中u 2的波形。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解根据互感同名端的定义,互感电压所以,u 2的定性波形如题图(c)所示。
3.已知周期电流i为正弦函数每个周期中t=0至(如题图所示)。
求此电流i的有效值。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解根据周期电流有效值的定义,电流i的有效值为4.非正弦周期电压如题图所示,求其有效值U。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解根据有效值的定义,有5.求题图所示电路中电压u C的有效值U C。

清华大学硕士电路原理-12(总分:100.00,做题时间:90分钟)一、解答题(总题数:12,分数:100.00)1.如图所示电路接在理想电压源上,求该电路的时间常数。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解电路的时间常数与独立源无关。
独立电压源置零后,从电容两端看入的电阻网络为电阻R 1与R 2并联,所以该电路的时间常数为2.如图所示电路接在理想电流源上,求该电路的时间常数。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解独立电流源置零后,从电容两端看入的电阻网络为电阻R 1与R 2串联,所以该电路的时间常数为τ=(R 1 +R 2 )C3.电路如下图所示,求开关S闭合后电路的时间常数。
(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解开关S闭合、独立电流源置零后的电路如下图所示。
下图中从电感两端看入的等效电阻为R eq =2+(4+2)//3=4Ω所以电路的时间常数为4.电路如下图所示。
t=0时打开开关S(换路前电路已达到稳态)。
求i(0 + )和(分数:8.00)__________________________________________________________________________________________ 正确答案:()解析:解由换路定律可得u C1 (0 + )=u C1 (0 - )=4V,u C (0 + )=u C (0 - )=8V0 +电路如下图所示,则5.电路如图所示,t=0时开关S闭合,求电容电压的初始值。

考研,对于现在的我而言已经成为了过去时,但现在想来依旧是那种感觉——值得记忆回味。
大半年的时间都在朝着这同一个目标而努力,哭过、笑过,但无论如何我还是走过来了,现在一切终于尘埃落定,希望可以把我的一些经历跟大家分享。
清华大学电路原理827全套考研资料详细介绍:(全网最全,不断更新)一.清华大学研究生入学考试电路原理1989年至2012年的打印版标准真题说明:由于清华大学是不出售历年真题及资料的,所以现在市场上流动的历年真题都是回忆手写版的,都没有答案,而且试卷有很多地方难以辨认,而且试卷上有很多做题痕迹,不便于自测。
所以此套清华题库精心编排的打印版真题清晰综合,适合模拟测试。
清华考研试题不公开市面上比较难买到,这是清华题库拿出来的一手内部资料应该是比较齐全的了。
由于出题老师比较固定,从本人今年考试经验看来,历年真题参考价值非常大。
强烈推荐!!二、绝对真实的清华大学2013年电路原理真题,适合电气及自动化考生。
研究生考试用,由于商品特殊只售20份,售完为止。
绝对原创,独此一家。
手写版本,2013年考生考场记录下来,有图,有文字,有数据,100%呈现,单卖120元!三、电路原理学习指导与习题集(第2版)复印版本《电路原理学习指导与习题集(第2版)》是电路原理课程的教学参考书,涵盖了电路原理课程的主要内容。
全书共分17章,包括电路元件与电路定律、电路的等效变换、线性电阻电路的一般分析方法、电路定理及应用、非线性电路、二端口网络、一阶电路、二阶电路、状态变量法、拉普拉斯变换、正弦稳态电路分析、有互感的电路、电路中的谐振、三相电路、周期性激励下电路的稳态响应、网络图论基础和均匀传输线。
附录为OrCAD/PSpice电路仿真分析简介。
每章均结合重点作了内容小结,给出了相应的例题及详细的解答,并指出了应注意的问题。
章后附有大量习题,内容丰富。
书末附有参考答案。
四、清华大学硕士研究生入学考试:电路原理试题选编(第2版)《清华大学硕士研究生入学考试:电路原理试题选编(第2版)》主要补充了近几年清华大学硕士研究生入学考试电路原理试题。
2013年清华大学电路原理考研真题
1、(1)理想变压器+并联谐振:理想变压器的副边借有并联的电感与电容,告诉了电感与电容支路的电流表读数相等,由这个条件可求出电路工作的频率值,再代入原边的电感值计算得到原边电路的阻抗,最后求出原边电流;(2)卷积:是一个指数函数和一个延时正比例函数的卷积,直接用公式计算即可,可以把指数函数选作先对称后平移的项,这样只需分三个时间段进行讨论即可;
2、三相电路:(1)电源和负载均为星形连接,且三相对称,直接抽单相计算线电流;(2)共B接法的二表法测电路的三相有功功率,要画图和计算两块功率表的读数,注意的读数为负数;(3)当A相负载对中性点短路后求各相电源的有功,先用节点法求出各相电流,再计算各相电源的有功功率;
3、理想运放的问题:共有2级理想运放,其中第一级为负反馈,第二级为正反馈,解答时先要判断出这一信息,然后(1)求第一级的输出,因为第一级运放是负反馈,故可以用“虚断”和“虚短”,得到输出(实为一个反向比例放大器);(2)求第二级的输出,因为是正反馈,所以“虚断”仍成立,但“虚短”不成立,不过,由正反馈的性质,运放要么工作在正向饱和区,要么工作在反向饱和区,即输出始终为,故可以假设输出为其中一个饱和电压,比较反相输入端和非反相输入端的电压值即可确定第二级的输出(实为一个滞回比较器);
4、一阶电路的方框图问题:动态元件是电容,它接在方框左端,首先告诉了方框右端支路上的电流的零输入响应,由此可得从电容两端看入的入端电阻,即为从方框左端看入的Thevenin等效电阻,其次可得到时刻的电量,画出这个等效电路图;然后改变电容值,改变电容的初始电压值,并在方框右端的支路上接上一个冲激电压源,求电容电压的响应:可以利用叠加定理,分解为零输入响应和零状态响应分别求解,零输入响应可根据前述Thevenin等效电阻直接写出,零状态响应可以先用互易定理(因为方框内的元件全是线性电阻,满足互易定理)结合前述“时刻的电量,画出这个等效电路图”得到左端的短路电流,再由Thevenin等效电阻进而得到从电容两端向右看入的Thevenin等效电路,然后先求阶跃响应,再求导得到冲激源作用下的冲激响应;最后叠加得到全响应;
5、列写状态方程:含有一个压控电流源的受控源,有2个电容和1个电感,用直接法,最后消去非状态变量即可得解答;
6、含有互感的非正弦周期电路(15分):(1)求电感电流,互感没有公共节点,无法去耦等效,只能用一般方法解,该题的电源有2种频率,有3个网孔,2个电感和1个电容,最关键的是左下角网孔的电源是电流源,因此可以设出电感电流的值,再由KCL表示出剩余支路的电流,最后对某一个网孔列写KVL,解方程即可得到要求的电感电流的值,只需列写一个方程,但要注意正确地写出互感电压的表达式;(2)求电流源发出的功率,由第一问的解求出电流源两端的电压,即可得到解答;
7、含有理想二极管的二阶电路:需要判断理想二极管何时关断、何时导通,这是解题的关键。
从0时刻开始,二极管关断,电路是一个二阶电路,求出电感电流的响应,直到二极管的端电压一直由增大到零,这就是所求临界点,即电感电流达到最大值的时间节点,此后二极管导通,左右两部分电路是2个独立的一阶电路。
因此(1)电路可以分为2个工作时间段,分别画出前述的二阶等效电路
和一阶等效电路;(2)解二阶电路,令,得到电感电流达到最大值的时刻,代入电感电流表达式得到电感电流最大值;(3)定性分析,若使得第二问的电感电流值达到最大的时间缩短一半,电感是应该增大还是减小?因为是定性分析,可由知,在很短的时间内,电感电压可看作不变,那么欲使电感电流达到最大值的时间缩短(一半),即使得电感电流的变化率增大,因此需要减小电感L的值;
8、Laplace变换法求解动态电路:先求换路前电容电压与电感电流的初始值,再画出换路后的运算电路,最后用节点法列一个方程即可得到解答,关键是对换路后的指数函数电压源做正确的拉氏变换;
9、二端口网络与非线性电阻电路的综合问题:告诉了二端口网络的T参数,先由T参数求出从非线性电阻两端向左端看入的Thevening等效电路,再用图解法或者假设-检验的方法确定直流工作点,然后求出动态电阻,画出小信号等效电路,得到小信号响应,最后合成得到所求非线性电阻的电流值;
10、网络图论:给出的电路含有一个压控电流源,给出的电路的图G,并给定了树支,求基本回路矩阵和基本割集,节点电压方程中的各个矩阵和相量;
11、求无损线的入端阻抗(8分):要是记得公式直接带入公式就能得到解答,记不住公式那就用无损线的正弦稳态解,两式相除即可得到入端阻抗,需要要先求参数与,并且注意的单位是弧度,要转化为角度,即,再求入端阻抗。