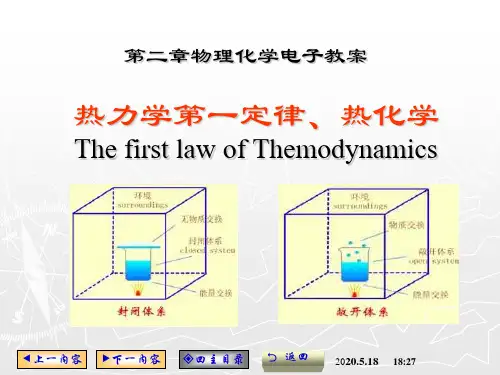
第二章多相多组分系统热力学§2.1 均相多组分系统热力学混合物和溶液都是一种多组分均相系统。
混合物：用来描述多种物质的气态、液态或固态均相系统，系统中所有物质用不分彼此的方法处理。
可以选用相同的方法研究每一个组分的性质。
溶液：用来描述多种物质的液态或固态均相系统。
相对含量较少的叫溶质，较多的叫溶剂。
对于溶质的溶剂需建立不同的标准研究。
一组成标度（组成表示法）1 混合物常用的组成标度B的质量分数w B=m B/mB的摩尔分数x B=n B/∑BB nB的物质的量浓度c B=n B/V2 溶质B常用的组成标度质量摩尔浓度：b B= n B / m A溶质B的摩尔分数x B=n B/∑BB n溶质B的物质的量浓度c B= n B/V不同浓度之间可以相互换算。
二偏摩尔量对于一定量的单组分单相封闭系统，一般只要两个状态变量就可以确定系统的状态。
而对与均相多组分系统大量实验事实说明：①均相多组分系统或均相敞开系统其容量性质如体积V ，热力学能U 等不仅是T ，p 的函数，还是系统中各组分物质的量n 的函数，因此要确定均相多组分系统的状态就必须考虑系统的组成。
②均相多组分系统的容量性质不具有简单的加和性，即V ≠∑B V (B)。
1 偏摩尔量的定义对于任一容量性质Z ，若系统中所含物质的量分别为n 1，n 2，…，则Z = f (T ，p ，n 1，n 2，…)Z 的微小变化d Z = n p T Z ,⎪⎭⎫⎝⎛∂∂d T +nT p Z ,⎪⎪⎭⎫ ⎝⎛∂∂d p + 1,,1dn n Z ncP T ⎪⎪⎭⎫⎝⎛∂∂ + 2,,2dn n Z ncP T ⎪⎪⎭⎫ ⎝⎛∂∂ +… =n p T Z ,⎪⎭⎫ ⎝⎛∂∂d T +nT p Z ,⎪⎪⎭⎫ ⎝⎛∂∂d p + c B B Z n ,p ,T n ∑⎪⎪⎭⎫ ⎝⎛∂∂d n B 等温、等压条件下d Z =cBBZ n ,p ,T n ∑⎪⎪⎭⎫⎝⎛∂∂d n B令： Z B =cB n ,p ,T n Z ⎪⎪⎭⎫ ⎝⎛∂∂Z B 表示系统中任意物质B 的偏摩尔量，Z 可为任一容量性质，例V B =c ,,B n p T n V ⎪⎪⎭⎫ ⎝⎛∂∂ G B =c ,,B n p T n G ⎪⎪⎭⎫ ⎝⎛∂∂ S B =c,,B np T n S ⎪⎪⎭⎫ ⎝⎛∂∂ 偏摩尔量的含义可从以下两个方面理解：① 指定T 、p 、各组分浓度不变的条件下，，往无限大量的系统中加入1摩尔物质B 所引起的体积的改变，称为物质B 的偏摩尔体积。
② 指定T 、p 下，在组成确定的有限系统中，加入无限小量（dn B ）的物质B ，引起系统体积的改变量dV 与dn B 之比值称为物质B 的偏摩尔体积。
2 偏摩尔量的集合公式Z = f (T ，p ，n 1，n 2，…)，定T 、p 下， d Z =∑BB B dn Z d n B ，将上式在T 、p 及组成不变（Z B =常数）的条件下积分∑=BB B n Z Z此式称为偏摩尔量的集合公式，该公式表明了体系的某容量性质与体系中各组分的物质的量和偏摩尔量之间的关系。
单组分系统中关于容量性质的许多关系式，在多组分系统中只要将容量性质换成相应的偏摩尔量，这些关系式仍然成立。
如H B =U B +pV B 、G B =H B -TS B 等。
3 Gibbs —Duhem 公式将集合公式Z=∑Z B n B 在T 、p 一定的条件下微分dZ=B BB B BB dZ n dn Z ∑∑+根据集合公式 dZ =∑BB B d n Z∑BB B d Z n = 0 Gibbs —Duhem 公式Gibbs —Duhem 公式表明，T 、p 一定的条件下，系统各组分偏摩尔量的变化是相互联系相互制约的。
4 偏摩尔量的求算三、 化学势及多组分系统的热力学基本方程1 化学势的定义在所有偏摩尔量中，偏摩尔Gibbs 自由能G B 最为重要，一方面是因为大多数化学反应和相变化是在等T , p 条件下发生的；另一方面，用Gibbs 自由能作判据时也是在等T , p 条件下。
因此，Gibbs 提出将偏摩尔Gibbs 自由能叫做化学势，用B μ表示。
B μ= c,,B n p T n G ⎪⎪⎭⎫⎝⎛∂∂ 对于均相多组分系统 G = f (T , p , n 1 , n 2 ,……) G 的全微分为d G =np T G ,⎪⎭⎫ ⎝⎛∂∂d T + nT p G ,⎪⎪⎭⎫ ⎝⎛∂∂d p +Cn P n G ,1⎪⎪⎭⎫ ⎝⎛∂∂d n 1 +Cn P n G ,2⎪⎪⎭⎫ ⎝⎛∂∂ d n 2 +……=np T G ,⎪⎭⎫ ⎝⎛∂∂d T + nT p G ,⎪⎪⎭⎫ ⎝⎛∂∂d p +c,,BB n p T n G ∑⎪⎪⎭⎫ ⎝⎛∂∂ d n B则 d G =np T G ,⎪⎭⎫⎝⎛∂∂d T + nT p G ,⎪⎪⎭⎫ ⎝⎛∂∂d p + ∑BB μd n B 偏摩尔自由能G B 就是B 组分的化学势B μ。
但不能说化学势就是偏摩尔自由能G B ，因为化学势还有其它定义。
对于均相多组分系统将状态函数U ，H ，F 都表示成特征变量与组成的函数：U = f (S ,V ,n 1,n 2,…) H = f (S , p ,n 1,n 2,…) F = f (T ,V ,n 1,n 2,…)全微分 d U =n V S U ,⎪⎭⎫ ⎝⎛∂∂d S + n S V U ,⎪⎭⎫ ⎝⎛∂∂d V +c,,B B nV S n U ∑⎪⎪⎭⎫⎝⎛∂∂d n B d U = T d S -P d V +c,,B Bn V S n U∑⎪⎪⎭⎫⎝⎛∂∂ d n B d H =Td S + Vd P +c,,B Bn P S n H∑⎪⎪⎭⎫⎝⎛∂∂d n B d F =-Sd T -Pd V +c,,B Bn V T n F∑⎪⎪⎭⎫⎝⎛∂∂d n B 以上关系式中各能量函数对n B 的偏微分均叫做组分B 的化学势，且对同一体系几种表达方式是完全等价的。
B μ= c,,B n p T n G ⎪⎪⎭⎫ ⎝⎛∂∂=c ,,B n V T n F ⎪⎪⎭⎫ ⎝⎛∂∂=c ,,B n V S n U ⎪⎪⎭⎫ ⎝⎛∂∂=c,,B n P S n H ⎪⎪⎭⎫⎝⎛∂∂ 3 均相多组分系统热力学基本方程 对多组分系统来说，热力学基本关系式为 d G = - S d T + V d p +∑BB μd n Bd F = - S d T - p d V +∑BB μd n Bd H = T d S + V d p +∑BB μd n Bd U = T d S - p d V +∑BB μd n B以上四式称之为多组分系统热力学基本方程，它只有在不考虑其它功(如表面功)的情况下才成立。
4 化学势的物理意义d G = - S d T + V d p +∑BBμd n B定T、P下，d G T,P=∑BBμd n BBμ的物理意义：化学势是一种广义的力，是一种强度因素，它是物质在两相中传递或者发生化学反应的推动力。
四化学势判据及其在相平衡和化学平衡体系的应用1 过程性质判据等温、等压下过程性质的判据为：d G T,P ≤'Wδ对于多组分变组成系统有d G T,P= ∑BBμd n B∑BBμd n B≤'Wδ式中：“＜”代表不可逆过程；“=”代表可逆过程。
2 自发方向及限度的判据①等T、P下过程自发方向及限度的判据是d G T,p≤0由于d G T,P=∑BBμd n B，所以∑BBμd n B成了自发方向与限度的判据，即＜0 为自发过程∑BBμd n B=0 达到平衡态＞0 为非自发过程化学势还可作为在T、V恒定，或S、p恒定，或S、V恒定的情况下过程方向与限度的判据。
②等T 、V 过程，d F T ,V = ∑BB μd n B ≤0“＜” 为自发过程，“=” 达到平衡态；“ ＞” 为非自发过程 ③等S 、V 过程，d U S ,V = ∑BB μd n B ≤0④等S 、P 过程，d H S ,P = ∑BB μd n B ≤0因此，化学势可以作为以上过程的共同判据。
3化学势在相平衡和化学平衡体系的应用 ①化学势在相平衡体系的应用定T 、P 下，d G T ,P = ∑BB μd n B ， 设有两相α和β相，设有dn B mol 的B 物质从α相转移到β相中，B B B B B B B dn dn dn dG dG dG )()(αββαβαμμμμ-=+-=+=a ） 设上述过程是在两相平衡条件下进行的 dG T ，P =00)(=-B B B dn αβμμ dn B ≠0 0=-αβμμB B αβμμB B =结论：两相平衡时体系中某一组分在两相中的化学势必相等，此为相平衡的条件之一，对多相平衡也适用。
b ）设上述过程是自发进行的，dG T ，P ＜0B B B dn )(αβμμ-＜0 dn B ＞0αβμμB B - ＜0 βμB ＜αμB结论：B 物质可以自发的由它化学势高的α相向化学势低的β相转移，直到两相中B 物质的化学势相等，即达到了该过程的限度——二相平衡。
②化学势在化学平衡体系的应用设任一反应 A+2B →3C 定T ，P 下d G T ,P = ∑BB μd n B = -μA dn - 2μB dn +3μC dn =（3μC -μA -2μB ）dna ）如反应处于平衡 dG T ，P =0 dn B ≠0 3μC -μA –2μB =0 3μC =μA + 2μB化学平衡条件：产物的化学势之和等于反应物的化学势之和。
b ）如反应是自发的 dG T ，P ＜0 （3μC -μA - 2μB ）dn ＜0 dn ＞03μC ＜μA + 2μB结论：化学反应自发的由化学势较高的一方向化学势较低的一方进行，直到两边的化学势相等。
五 化学势与温度、压力的关系 1 化学势μ与压力的关系c c ,,,B ,,,B ,B n p T n T n T n p T n T p G n n G p p ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∂∂=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎪⎭⎫⎝⎛∂∂μ=c,,B n p T n G ⎪⎪⎭⎫ ⎝⎛∂∂=V B 所以对于定温定组成系统有 nT p ,B ⎪⎪⎭⎫⎝⎛∂∂μ=V Bd B μ= V B d T通常情况下V B > 0 ，温度、组成不变时化学势随压力升高而增加。
特别是对纯物质，由于V m (g) >>V m (l )≈V m (s) , 所以压力对气态物质的化学势影响较大，而对凝聚态的影响较小。
