- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
使横截面上不出现拉应力 的压力作用点的集合,称 为截面核心。 要使坐标为r, s 的C点的应 力为零,则由
y p y0 i y pr i
2 z 2 z
z p z0 i zps i
2 y 2 y
1 1
直线pq的方程
22
要使坐标为r, s 的C点的应 力为零,则由
y p y0 i y pr i
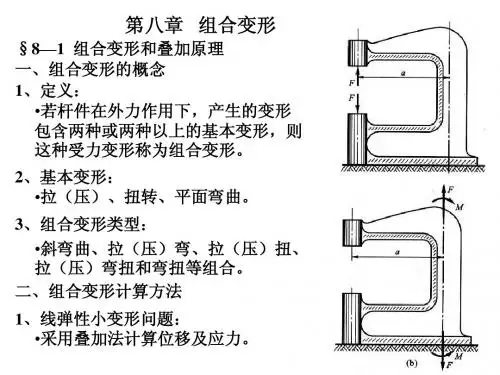
这是组合变形问 题 压弯组合。
5
这是组合变形问题 压弯组合。 求约束反力 取AB, 受力如图
M
A
(F ) 0
F 42 kN H 40 kN, V 12.8 kN
内力图 危险截面 C 截面
6
H 40 kN, V 12.8 kN
内力图 危险截面 C 截面
M C 12 kNm, N 40 kN
设计截面的一般步骤 先根据弯曲正应力选择工字钢型号; 再按组合变形的最大正应力校核强度,必要 时选择大一号或大二号的工字钢; 若剪力较大时,还需校核剪切强度。
7
M C 12 kNm, N 40 kN
设计截面的一般步骤 先按弯曲正应力选择工字钢型号; 再按组合变形的最大正应力校核强度,必要 时选择大一号或大二号的工字钢; 若剪力较大时,还需校核剪切强度。 按弯曲正应力选择工字钢型号
中性轴方程 设中性轴在y轴和z轴上的 截距为ay, az ,则有:
由上可知: 1) 压力作用点与中性轴分别位于形心的两侧; 2) 中性轴将横截面分为两部分,一部分受压, 19 一部分受拉;
i i a y , az yp zp
2 z
2 y
由上可知: 1) 压力作用点与中性轴分别位于形心的两侧; 2) 中性轴将横截面分为两部分,一部分受压, 一部分受拉; 3) 在截面的周边上,切 线与中性轴平行的点 的应力为极值。
2
3
Wt 2W
M T 1 M 2 T 2 r 3 4 W 2W W 1 2 2 同样可得 r 4 M 0.75T W
35
M T 1 M 2 T 2 r 3 4 W 2W W 1 2 2 同样可得 r 4 M 0.75T W
A 15 10 m , zo 7.5 cm, 4 I y 5310 cm
2
3
求内力(作用于截面形心)
10
几何参数
A 15 10 m , zo 7.5 cm, 4 I y 5310 cm
2
3
求内力(作用于截面形心) 取研究对象如图
N P kN, 2 M y 42.5 10 P kNm
最大拉应力 最大压应力
t max
P 425 7.5P MPa 15 5310
P 425 12.5P MPa 15 5310
c max cmax
由抗拉强度条件
t max [ t ] 30 MPa
P 45.1 kN P 171.3 kN
截面核心 在土木工程中,对于受 偏心压缩的混凝土、大 理石等柱子,要求在横截面上不出现拉应力。 20
截面核心 在土木工程中,对于受 偏心压缩的混凝土、大 理石等柱子,要求在横 截面上不出现拉应力。
使横截面上不出现拉应力 的压力作用点的集合,称 为截面核心。
要使坐标为r, s 的C点的应 力为零,则由
M y Pz p
应力
坐标为 y, z 的B点的应力:
P A Py p y Mzy Iz Iz
M yz Iy
Pz p z Iy
16
P A Py p y Mzy Iz Iz
M yz Iy
37
解:
求外力 力偶矩
D 皮带张力 ( F f ) m 又 F f 600 2 F 465 N, f 135 N d1 齿轮作用力 P cos 20 Pn 925 N m n 2
N m 9549 n 21.7 Nm
将各力向轴线简化
38
F 465 N, f 135 N
a点坐标
2 z
2 y
i i ya , z a ay az
2 z
2 y
设AB为中性轴
b点
同理可确定c, d, e点。
连线可得到截面核心。
25
例 3 (书例9.3) 已知: 矩形截面 求:截面核心。 解:对矩形截面
b h 2 i , iz 12 12
2 y
2
2
设AB为中性轴
材 料 力 学
第八章 组 合 变 形
2013年7月27日
1
第八章
组合变形
本章内容:
1 组合变形和叠加原理 2 拉伸或压缩与弯曲的组合 3 偏心压缩和截面核心 4 扭转与弯曲的组合 5 组合变形的普遍情况
2
§8. 1 组合变形与叠加原理
1 组合变形 基本变形 拉伸、压缩 剪切 组合变形 有两种或两种以上的 基本变形同时发生。
中性轴位置 设中性轴上的点的坐标 为 y0, z0。
在上式中令为零,得:
y p y0 z p z 0 P (1 2 2 ) 0 A iz iy y p y0 z p z 0 2 1 中性轴方程 2 iz iy
18
y p y0 i
2 z
z p z0 i
2 y
1
扭转
弯曲
求解组合变形的方法 将载荷分为几组分别产生 基本变形的载荷,然后应 用叠加原理。
3
2 叠加原理 如果内力、应力、变形等与外力成线性关系, 则复杂受力情况下组合变形构件的内力、应 力、变形等可以由几组产生基本变形的载荷 单独作用下的内力、应力、变形等的叠加而 得到,且与各组载荷的加载次序无关。
MC [ ] W
MC 3 120 cm W [ ] 选16号工字钢 W 141 cm3 , A 26.13 cm 2
8
按最大正应力校核强度
按弯曲正应力选择工字钢型号
MC [ ] W
MC 3 120 cm W [ ] 选16号工字钢 W 141 cm3 , A 26.13 cm 2
截面核心的确定
设AE为中性轴 中性轴的截距为ay, az, 由:
i i a y , az yp zp
a点坐标
2 z
2 y
i i ya , z a ay az
2 z
2 y
设AB为中性轴
24
b点
截面核心的确定
设AE为中性轴 中性轴的截距为ay, az, 由:
i i a y , az yp zp
内力图如图 危险截面 E截面 E截面的内力
D T P 2 Pr ab M y max l Pab M z max l
31
E截面的内力
D T P 2 Pr ab M y max l Pab M z max l
对圆截面杆 可将两个方向的弯矩按 矢量合成。
M M
2 y max
弯曲切应力 一般可忽略 危险点的应力状态 相当应力
r 3 4
2
2
r 4 3
2
2
34
T Wt
M W
2 2
2 2
相当应力
r 3 4 , r 4 3
D
32
2
3
用内力表示的相当应力
对圆截面杆 W
, Wt
D
16
Pz p z Iy
惯性矩可表为: I Ai 2 , I Ai 2 z z y y
中性轴位置 设中性轴上的点的坐标为 y0, z0。
yp y zpz P (1 2 2 ) A iz iy
17
yp y zpz P (1 2 2 ) A iz iy
a点坐标
h AB直线的截距为: a y , az 2 2 2 iy iz h 由:ya , za ya , z a 0 ay az 6
26
设AB为中性轴 a点坐标 AB直线的截距为:
h a y , az 22 2 iy iz 由:ya , za ay az
2 z 2 z
z p z0 i zps i
2 y 2 y
1 1
直线pq的方程 当压力作用点在直线pq上移动时,C点的应力保 持为零。 中性轴通过C点,但方位不断变化。
截面核心的确定
23
当压力作用点在直线pq上移动时,C点的应力保 持为零。 中性轴通过C点,但方位不断变化。
叠加原理成立的条件 (1) 应力应变关系为线性关系,即满足胡克定 律; (2) 变形是小变形,可以用原始尺寸原理。 下面的讨论,都假设用叠加原理的条件成立。 4
§8. 2 拉伸或压缩与弯曲的组合
例 1 (书例9.1) 已知:P = 8kN, AB为工字钢, 材料为A3钢, [] = 100MPa。 求: 工字钢型号。 解: AB受力如图
2
2
矩形截面杆的弯扭组合变形问题
两个方向的弯矩不宜合成,可 分别计算应力。 扭转切应力按矩形截面扭转公 式计算。 T
max
hb
2