当前位置：文档之家 › 数字电路与逻辑设计 第02章 习题解答

数字电路与逻辑设计 第02章 习题解答

  • 格式：pdf
  • 大小：258.61 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

数字逻辑与数字系统设计第2-3章客观题

数字逻辑与数字系统设计第2-3章客观题

（）1、数字电路又称为开关电路、逻辑电路。

答案：正确（）2、二极管、三极管、场效应管是常用的开关元件。

答案：正确（）3、最基本的逻辑关系是：与、或、非。

答案：正确（）4、高电平用0表示，低电平用1表示，称为正逻辑。

答案：错误（）5、TTL型门电路比CMS型门电路开关速度快。

答案：正确（）6、逻辑表达式是逻辑函数常用的表示方法。

答案：正确（）7、用真值表表示逻辑函数，缺乏直观性。

答案：错误（）8、逻辑图是最接近实际的电路图。

答案：正确（）9、由真值表得到的逻辑函数一般都要经过化简。

答案：正确（）10、组合电路的特点是：任意时刻的输出与电路的原状态有关。

答案：错误（）11、1+A＝1答案：正确（）12、AB+A＝A（）13、将实际问题转换成逻辑问题第一步是要先写出逻辑函数表达式。

答案：错误14、异或函数与同或函数在逻辑上互为反函数。

（对）每个最小项都是各变量相“与”构成的，即n个变量的最小项含有n个因子。

（对）15、因为逻辑表达式A+B+AB=A+B成立，所以AB=0成立。

（错）16、逻辑函数F=A B+A B+B C+B C已是最简与或表达式。

（错）17、利用约束项化简时，将全部约束项都画入卡诺图，可得到函数的最简形式。

（错）18、卡诺图中为1的方格均表示逻辑函数的一个最小项。

（对）19、在逻辑运算中，“与”逻辑的符号级别最高。

（错）20、标准与或式和最简与或式的概念相同。

（对）21、数字电路中用“1”和“0”分别表示两种状态，二者无大小之分。

（对）22、格雷码具有任何相邻码只有一位码元不同的特性。

（对）23、所有的集成逻辑门，其输入端子均为两个或两个以上。

（错）24、根据逻辑功能可知，异或门的反是同或门。

（对）25、逻辑门电路是数字逻辑电路中的最基本单元。

（对）26、TTL和CMOS两种集成电路与非门，其闲置输入端都可以悬空处理。

（错）27、74LS系列产品是TTL集成电路的主流，应用最为广泛。

(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)

(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
3-6
3-7
3-8
3-9
3-10
求减数的补码，然后与被减数相加即可。电路图如下：
3-11
3-12
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
3-13
(1)真值表：
（2）电路图
3-14
3-15
第四章习题
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-10
RSDRSJK RST
4-11
(1)转换真值表
1 1 0 1
1 1 1 0
1 1 1 1
1 0 1 0
0 0 0 0
0 0 0 1
0 0 1 0
00 11
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
××××
××××
××××
××××
××××
1×0×1×0×
0×0×0××1
0×0××1 1×
0×0××0×1
0××1 1×1×

数字电路与逻辑设计(曹国清)答案

数字电路与逻辑设计(曹国清)答案

数字电路与逻辑设计（曹国清）答案第一章数字逻辑习题1．1数字电路与数字信号1.1.2 图形代表的二进制数0101101001．1．4一周期性数字波形如图题所示，试计算：（1）周期；（2）频率；（3）占空比例MSBLSB0 1 2 11 12 （ms）解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100%=10%1.2数制1.2.2将下列十进制数转换为二进制数，八进制数和十六进制数（要求转换误差不大于 42. （2）127 （4）2.718解：（2）（127）D=-1=（10000000）B-1=（1111111）B=（177）O=（7F）H 72 （4）（2.718）D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码：（1）43 （3）254.25解：（43）D=（01000011）BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示：P28（1）+ （2）@ （3）you (4)43解：首先查出每个字符所对应的二进制表示的ASCⅡ码，然后将二进制码转换为十六进制数表示。

（1）“+”的ASCⅡ码为0101011，则（00101011）B=（2B）H（2）@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中，已知输入信号A，B`的波形，画出各门电路输出L的波形。

解: (a)为与非， (b)为同或非，即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)ABABAB⊕=+（A⊕B）=AB+AB解：真值表如下ABAB⊕ABABAB⊕AB+AB0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 0 1 1 1由最右边2栏可知，与AB+AB的真值表完全相同。

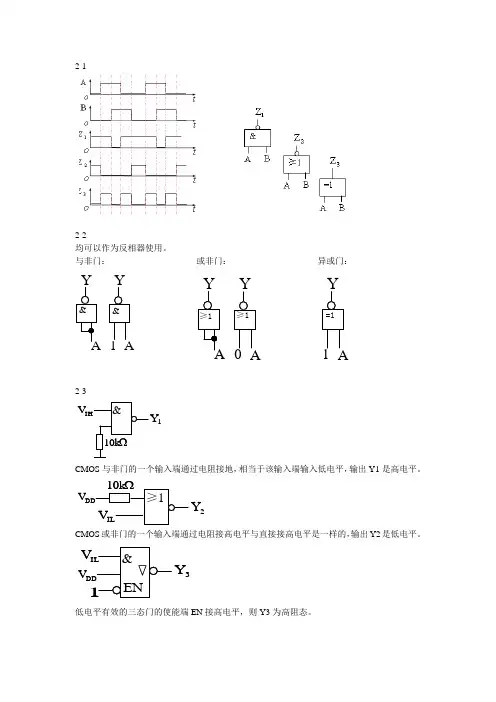
数字逻辑第二章课后答案

数字逻辑第二章课后答案

2-1
2-2
均可以作为反相器使用。

与非门：
或非门：
异或门：
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地，相当于该输入端输入低电平，输出Y1是高电平。

2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的，输出Y2是低电平。

V 3
Y V 低电平有效的三态门的使能端EN 接高电平，则Y3为高阻态。

4
Y V
与或非门的一个与门输入全为高电平，则输出Y4是低电平。

2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ，T1`和T2截止，Y=Z （高阻）。

当0=EN ，T1`导通，A A Y ==。

2-7
（1）忽略所有门电路的传输延迟时间，除去开始的一小段时间，与非门的两个输入端总有一个是低电平，输出一直为高电平。

（2）考虑每个门都有传输延迟时间。

假设1级门的传输延迟时间为tpd ，则与非门的两个输入端的输入信号变化实际上并不是同时的。

信号A 经过两级门的传输延迟，比信号B 要晚2tpd 时间到达与非门的输入端。

因此，将出现,在短暂时间里，两个输入端的输入信号都是高电平的情况，输出电压波形出现毛刺。

《数字电路-分析与设计》第二章习题及解答 北京理工大学出版社

《数字电路-分析与设计》第二章习题及解答 北京理工大学出版社
右边= A(BC+BC)+A(BC+BC)= ABC+ABC+ A(B+C)(B+C) =ABC+ABC+ABC+ABC=左边
5. A ⊕ B = A ⊕ B = A ⊕ B ⊕1
证明： 左边=AB+AB 中间= AB+AB=(A+B)(A+B)=AB+AB=左边 右边= (AB+AB)1+(AB+AB)1= AB+AB=中间 或者：根据 1⊕A=A，右边=中间
F1=(A+B)(B+C)(C+A)=ABC+ABC F2=(A+B)(B+C)(C+A)=ABC+ABC=F1 所以 F1=F2
习题
2． F1 = ABC + A B C ， F2 = AB + BC + CA
由 1.知：F1=F2
3． F1 = C D + A B + BC ， F2 = ABC + AB D + BC D
= AB + AC + BC
F = ( A + B) ⋅ ( A + C) ⋅ (B + C) = ( A + AB + AC + BC) ⋅ (B + C) = AB + ABC + BC + AC + ABC + AC + BC = AB + AC + BC
2-12 证明下列等式。
1. A ⊕ 0 = A
9. A( A + B ) = A
证明：左边=A+AB=A=右边，得证。 用真值表法略。 2-10 用逻辑代数演算证明下列等式。

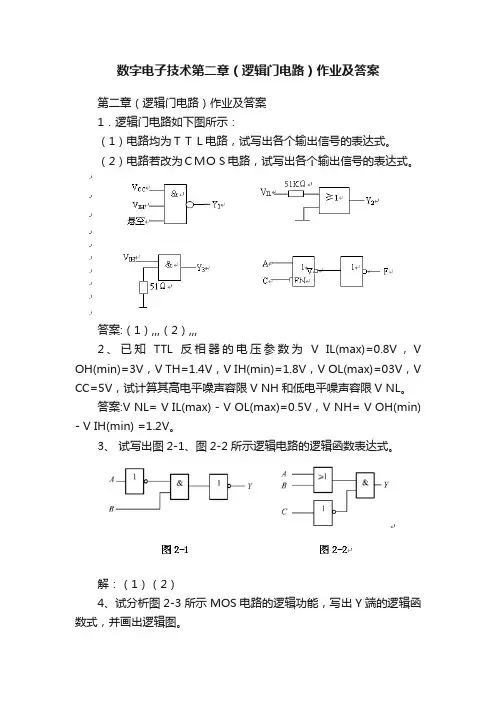
数字电子技术第二章（逻辑门电路）作业及答案

数字电子技术第二章（逻辑门电路）作业及答案

数字电子技术第二章（逻辑门电路）作业及答案第二章（逻辑门电路）作业及答案1．逻辑门电路如下图所示：（1）电路均为ＴＴＬ电路，试写出各个输出信号的表达式。

（2）电路若改为ＣＭＯＳ电路，试写出各个输出信号的表达式。

答案:（1）,,,（2）,,,2、已知TTL反相器的电压参数为V IL(max)=0.8V，V OH(min)=3V，V TH=1.4V，V IH(min)=1.8V，V OL(max)=03V，V CC=5V，试计算其高电平噪声容限V NH和低电平噪声容限V NL。

答案:V NL= V IL(max) - V OL(max)=0.5V，V NH= V OH(min) - V IH(min) =1.2V。

3、试写出图2-1、图2-2所示逻辑电路的逻辑函数表达式。

解：（1）（2）4、试分析图2-3所示MOS电路的逻辑功能，写出Y端的逻辑函数式，并画出逻辑图。

5、试简要回答下列问题。

（1）有源（图腾柱）输出与集电极开路（OC）输出之间有什么区别？解：OC门输出端只能输出低电平和开路状态，其输出级需要上拉电阻才能输出高电平，且上拉电源可以与芯片电源不同，因此常用于不同电源电压芯片之间实现信号电平变换，OC门输出端可以并联实现线与；有源输出可以输出低电平与高电平，两个有源输出端连接在一起时，若是一个输出端输出高电平，另外一个输出端输出低电平时，可引起较大电流损坏输出级。

（2）TTL逻辑电路输入端悬空时，可视为输入高电平信号处理，而CMOS逻辑电路输入端则不允许悬空使用，试说明其原因。

解：因为CMOS电路的输入端具有非常高的输入阻抗，容易受到干扰，一旦受到干扰后，会使输出电平发生转换，产生功耗，因此输入端不能悬空，应该连接确定的逻辑电平。

6.请查阅74LS00芯片手册（常规温度范围的），回答如下问题：（1）电源电压范围；（2）输出高电平电压范围；（3）输出低电平电压范围；（4）输入高电平电压范围；（5）输入低电平电压范围；（6）该芯片的电源电流；（7）典型传播延迟时间；（8）扇出系数。

数字电路与系统设计：第2章习题答案

数字电路与系统设计：第2章习题答案

习题目录2.1 (2)2.2 (2)2.3 (2)2.4 (3)2.5 (3)2.6 (4)2.7 (4)2.8 (4)2.9 (4)2.10 (4)2.11 (5)2.12 (5)2.13 (7)2.14 (8)2.1 有A 、B 、C 三个输入信号，试列出下列问题的真值表，并写出最小项表达式∑m （ ）。

（1）如果A 、B 、C 均为0或其中一个信号为1时。

输出F=1，其余情况下F=0。

（2）若A 、B 、C 出现奇数个0时输出为1，其余情况输出为0。

（3）若A 、B 、C 有两个或两个以上为1时，输出为1，其余情况下，输出为0。

F 1m 4）F 2m ）3m 7）2.2 试用真值表证明下列等式：（1）A ⎺B+B ⎺C+A ⎺C=ABC+⎺A ⎺B ⎺C （2）⎺A ⎺B+⎺B ⎺C+⎺A ⎺C=AB BC AC 证明：（1）真值表相同，所以等式成立。

（真值表相同，所以等式成立。

2.3 对下列函数，说明对输入变量的哪些取值组合其输出为1？ （1）F （A,B,C ）=AB+BC+AC（2）F （A,B,C ）=(A+B+C)(⎺A+⎺B+⎺C) （3）F （A,B,C ）=(⎺AB+⎺BC+A ⎺C)AC解：本题可用真值表、化成最小项表达式、卡诺图等多种方法求解。

（1）F 输出1的取值组合为：011、101、110、111。

（2）F 输出1的取值组合为：001、010、011、100、101、110。

（3）F输出1的取值组合为：101。

2.4试直接写出下列各式的反演式和对偶式。

(1)F(A,B,C,D,E)=[(A⎺B+C)·D+E]·B(2) F(A,B,C,D,E)=AB+⎺C⎺D+BC+⎺D+⎺CE+B+E(3) F(A,B,C)=⎺A⎺B+C ⎺AB C解：(1) ⎺F=[(⎺A+B)·⎺C+⎺D]·⎺E+⎺BF'=[(A+⎺B)·C+D]·E+B(2) ⎺F=(⎺A+⎺B)(C+D)·(⎺B+⎺C)·D·(C+⎺E)·⎺B·⎺EF'=(A+B)(⎺C+⎺D)·(B+C)·⎺D·(⎺C+E)·B·E(3)⎺F=(A+B)·⎺C+ A+⎺B+CF'=(⎺A+⎺B)·C+⎺A+B+⎺C2.5用公式证明下列等式：(1)⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D=⎺A+BC(2)AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=⎺A + B +⎺C+⎺D证明：(1) ⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D ——⎺A⎺C⎺D被⎺A⎺C削去=⎺A(⎺B+⎺C)+BC=⎺A BC+BC ——削去互补因子=⎺A+BC(2) AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+BC D+BC ——增加冗余因子BC，为了削去BCD中的BC =AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C⎺D ——B⎺CD与BCD合并成BD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C ——BD与B⎺C⎺D削去互补因子=⎺BC⎺D+BD+ACD+⎺BCD+B⎺C ——⎺AB⎺C⎺D被B⎺C削去=⎺BC+BD+ACD+B⎺C ——⎺BC⎺D与⎺BCD合并=⎺BC+BD+CD+ACD+B⎺C ——增加CD，可削去ACD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=A⎺B⎺C (BC+BC⎺D)+⎺A+B+⎺D ——BC+BC⎺D削去互补因子=A⎺B⎺C (⎺B+⎺C+⎺D)+⎺A+B+⎺D=A⎺B⎺C +A⎺B⎺C⎺D+⎺A+B+⎺D=A⎺B⎺C+⎺A+B+⎺D=⎺A+ B +⎺C+⎺D2.6已知⎺ab+a⎺b=a⊕b,⎺a⎺b+ab=a b,证明：（1）a⊕b⊕c=a b c（2）a⊕b⊕c=⎺a ⎺b ⎺c证明：(1)a⊕b⊕c=(a⊕b)⊕c=a⊕b · c+(a⊕b)·⎺c=(a b)·c+ a b⎺c=a b c(2)(a⊕b)⊕c = (a⊕b) c=a b c=a b ⎺c=⎺a ⎺b ⎺c2.7试证明：（1）若⎺a⎺b+ a b=0则a x+b y=a⎺x + b⎺y证明：⎺a⎺b+ a b=0 即a b=0 ∴a =⎺bax + by =⎺bx + by = ⎺bx · by=(b+⎺x)(⎺b+⎺y)=b⎺y+⎺b⎺x+⎺x⎺y=a⎺x+b⎺y（2）若⎺a b+a⎺b=c，则⎺a c + a⎺c=b证明：a⊕b=c => a⊕b⊕c=c⊕c => a⊕b⊕c=0 => a⊕b⊕c⊕b=0⊕b => a⊕c=b2.8将下列函数展开成最小项之和：（1）F（ABC）=A+BC（2）F（ABCD）=（B+⎺C）D+(⎺A+B) C（3）F(ABC)=A+B+C+⎺A+B+C解：（1）F（ABC）=A+BC=A（B+⎺B）(C+⎺C)+(A+⎺A)BC=⎺ABC+A⎺B⎺C+A⎺BC+AB⎺C=∑m(3,4,5,6)(2) F（ABCD）=（B+⎺C）D+(⎺A+B) C=BD+⎺CD+⎺AC+BC=∑m(1,3,5,6,7,9,13,14,15)(3) F(ABC)=A+B+C+⎺A+B+C=∑m(0,2,6)2.9将题2.8中各题写成最大项表达式，并将结果与2.8题结果进行比较。

数字逻辑电路与系统设计[蒋立平主编][习题解答]

数字逻辑电路与系统设计[蒋立平主编][习题解答]

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

《电子技术基础》第五版(数字部分)高教版课后答案

《电子技术基础》第五版(数字部分)高教版课后答案

1．1 数字电路与数字信号第一章 数字逻辑习题1.1.2 图形代表的二进制数MSBLSB 0 1 211 12（ms ）解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100%=10% 数制1.2.2 将下列十进制数转换为二进制数，八进制数和十六进制数（要求转换误差不大于 2 （2）127 （4）解：（2）（127）D=27-1=（）B-1=（1111111）B =（177）O=（7F ）H （4）（）D=B=O=H 二进制代码1.4.1 将下列十进制数转换为 8421BCD 码： （1）43 （3） 解：（43）D=（01000011）BCD1.4.3 试用十六进制写书下列字符繁荣 ASC Ⅱ码的表示：P28 （1）+ （2）@ （3）yo u (4)43解：首先查出每个字符所对应的二进制表示的 ASC Ⅱ码，然后将二进制码转换为十六进制 数表示。

（1）“+”的 ASC Ⅱ码为 0101011，则（00101011）B=（2B ）H （2）@的 ASC Ⅱ码为 1000000,(01000000)B=(40)H(3)you 的 ASC Ⅱ码为本 1111001,1101111,1110101,对应的十六进制数分别为79,6F,75 (4)43 的 ASC Ⅱ码为 0110100,0110011,对应的十六紧张数分别为 34,33 逻辑函数及其表示方法解: (a)为与非， (b)为同或非，即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3) A⊕B AB AB（A⊕B）=AB+AB解：真值表如下A B A⊕BAB AB A⊕BAB+AB0 0 1 11111111111A (1BC ) ACDCDEA ACDCDEACD CDEACD E2.1.4 用代数法化简下列各式(3) ABC B C)A⋅B A⋅B(A B)(A B)1BAB ABABBABAB(9) ABC DABD BC D ABCBD BC解： ABC DABDBC DABCBD BCB ( ACD )L D ( AC)2(3)(L AB)(C D)2.2.2 已知函数 L（A，B，C，D）的卡诺图如图所示，试写出函数 L 的最简与或表达式解：L( A, B, C, D) BC D BCD B C D ABD2.2.3 用卡诺图化简下列个式（1）ABCD ABCD AB AD ABC3解：ABCD ABCD AB AD ABCABCD ABCD AB CC DDAD B B CCABC D D)()()()()(ABCD ABCD ABC D ABCD ABC D ABC D ABC D（6）L( A, B, C, D ) ∑m解：(0, 2, 4, 6,9,13)∑d(1, 3, 5, 7,11,15)L AD（7）L( A, B, C , D )∑m 解: (0,13,14,15)∑d(1, 2, 3, 9,10,11)L AD AC AB42.2.4 已知逻辑函数L AB BC C A，试用真值表,卡诺图和逻辑图（限用非门和与非门）表示解:1>由逻辑函数写出真值表A11112>由真值表画出卡诺图B1111C1111L1111113>由卡诺图,得逻辑表达式L AB BC AC 用摩根定理将与或化为与非表达式L AB BC AC AB⋅B C⋅AC4>由已知函数的与非-与非表达式画出逻辑图5第三章习题MOS逻辑门电路3.1.1 根据表题所列的三种逻辑门电路的技术参数，试选择一种最合适工作在高噪声环境下的门电路。

数字电路课后习题答案第二章

数字电路课后习题答案第二章

2.8
(a)
(b)
2.9
(a)
(b)
2.10 (a)
(b)
(c)
2.11 decimal signed-magnitude two’s-magnitude one’s-complement 2.12 (a)
11010100 (b) 101110011 (c) 01011101 (d) 00100110 + 10101011 + 11010110 + 00100001 + 01011010 ------------------------------------------------------------------------------------------------------------------------01111111 10001111 01111101 10000000 yes no no yes
2.6
(a) (c) (e) (g) (i)
125 10 = 1111101 2 209 10 = 11010001 2 132 10 = 1000100 2 727 10 = 10402 5 1435 10 = 2633 8 1100010 110101 + 11001 ------------------------1001110 110000 110101 - 11001 -----------------------011100 1372 + 4631 ------------------6223 1372 + 4631 ------------------59A3 (b)
2.7
(a)
111111110 (d) 11000000 1011000 (c) 11011101 101110 1110010 + 1100011 + 100101 + 1101101 ------------------------------------------------------------------------------------101000000 1010011 11011111 0011010 000010 (c) 11000100 (d) 1110010 11011101 101110 - 1101101 - 1100011 - 100101 ------------------------------------------------------------------------------------0000101 01111010 001001 47135 + 5125 ------------------54262 4F1A5 + B8D5 ---------------------5AA7A + 18 00010010 00010010 00010010 (c) 175214 (d) 110321 + 152405 + 56573 ---------------------------------------------347621 167114 F35B + 27E6 -------------------11B41 + 115 01110011 01110011 01110011 (d) 1B90F + C44E --------------------27D5D +79 01001111 01001111 01001111 –49 10110001 11001111 11001110 –3 10000011 11111101 11111100 –100 11100100 10011100 10011011

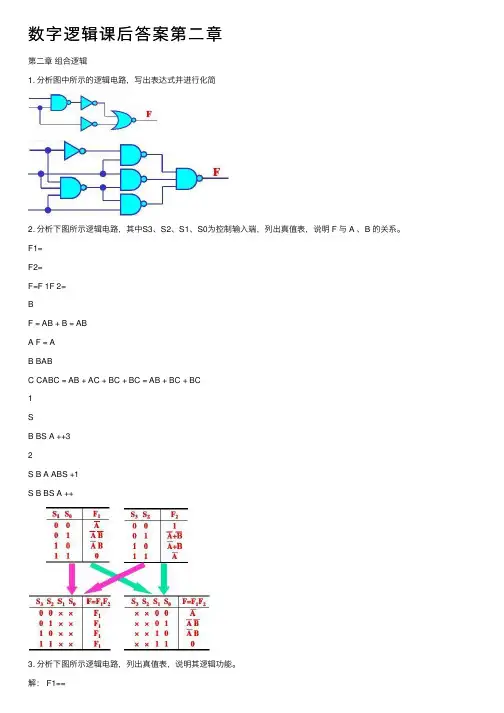
数字逻辑课后答案第二章

数字逻辑课后答案第二章

数字逻辑课后答案第⼆章第⼆章组合逻辑1. 分析图中所⽰的逻辑电路，写出表达式并进⾏化简2. 分析下图所⽰逻辑电路，其中S3、S2、S1、S0为控制输⼊端，列出真值表，说明 F 与 A 、B 的关系。

F1=F2=F=F 1F 2=BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC1SB BS A ++32S B A ABS +1S B BS A ++3. 分析下图所⽰逻辑电路，列出真值表，说明其逻辑功能。

解： F1==真值表如下：当B ≠C 时， F1=A 当B=C=1时， F1=A 当B=C=0时， F1=0裁判判决电路，A 为主裁判，在A 同意的前提下，只要有⼀位副裁判（B ，C ）同意，成绩就有效。

F2=真值表如下：CB BC A C AB C B A +++ABCC B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111AC BC AB C A C B B A ++=++当A 、B 、C 三个变量中有两个及两个以上同时为“1”时，F2 = 1 。

4.图所⽰为数据总线上的⼀种判零电路，写出F 的逻辑表达式，说明该电路的逻辑功能。

解：F=只有当变量A0~A15全为0时，F = 1；否则，F = 0。

因此，电路的功能是判断变量是否全部为逻辑“0”。

5. 分析下图所⽰逻辑电路，列出真值表，说明其逻辑功能解：因此，这是⼀个四选⼀的选择器。

6. 下图所⽰为两种⼗进制数代码转换器，输⼊为余三码，输出为什么代码？解：A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1000011111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=这是⼀个余三码⾄8421 BCD 码转换的电路7. 下图是⼀个受 M 控制的4位⼆进制码和格雷码的相互转换电路。

《数字电路与逻辑设计》习题课 (2)

《数字电路与逻辑设计》习题课 (2)
10/10
状态定义： S0:初始状态。 S1:收到五角硬币。 S2:收到一元硬币。 S3:收到一元五角硬币。 并入S0状态。
00/00 AB/YZ
S0
01/10 10/11
01/00 10/00
S2
S1 00/00 01/00
00/00 例1原始状态转移图
例2、分析图所示计数器电路，说明是模长为多少的 计数器，并列出状态转移表。
6
C
&
1 1
A & ?
Z
X
&
N
A X
&
1 & J
1
C
R 1 & K
解：1）分析电路结构：该电路是由七个与非门 及一个JKFF组成，且CP下降沿触发，属于米 勒电路，输入信号X1，X2，输出信号Z。
2）求触发器激励函数：J=X1X2，K=X1X2 触发器次态方程：
Qn+1=X1X2Qn+X1X2Qn=X1X2Qn+(X1+X2)Q
第六章复习
计数器的分析
❖ 同步、异步分析步骤：由电路触发器激励 函数(公式和图解）状态转移表分析模 长和自启动性。 用图解法，注意高低位顺序，一般数码越高 位权越高：Q3Q0
❖ 移存型计数器属于同步计数器，只要求出第 一级触发器的次态方程和初始状态，就可以 写出状态转移表。
计数器的设计
❖ 同步计数器的设计：状态转移表激励函数 和输出函数(自启动性检查)电路图。
❖ 7490只能异步级联，M=100。
❖ 74194级联可实现8位双向移存器
MSI实现任意进制计数器(M<N)
❖ 反馈法：异步清0法和同步置数法。注意： 用LD端置全1（置最大数法）时，反馈状 态对应编码中出现0的端口需通过非门送入 反馈门。

数字电路逻辑设计课后习题解答(王毓银+第三版+无水印)

数字电路逻辑设计课后习题解答(王毓银+第三版+无水印)

7421 码
0000 0001 0010 0011 0100 0101 0110 1000 1001 1010
8421 码
0000 0011 0010 0101 0100 0111 0110 1001 1000 1011
解（31.67）10＝（01100100.10011010）余3BCD码 （3）（465）10＝（？）2421BCD码 解（465）10＝（010011001011）2421BCD码 （4）（110110100011）631－BCD码＝（？）10 解 （110110100011）631－BCD码＝（870）10 （5）（1000020220010111）8421BCD码＝（？）10 解 （1000020220010111）8421BCD码＝（8597）10
第 2 章 逻辑函数及其简化
1.列出下述问题的真值表，并写出逻辑表达式。 （1）有 a ，b ，c ，2 个输入信号，如果 3 个输入信号均为 0 或其中一个为 1 时，输出信 号 Y＝1，其余情况下，输出 Y＝0； （2）有 a ，b ，c ，2 个输入信号，当 3 个输入信号出现奇数个 1 时，输出 F 为 1，其余 情况下，输出 F 为 0； （3）有 3 个温度探测器，当探测的温度超过 60℃时，输出控制的信号为 1；如果探测的温 度低于 60℃是，输出控制信号 Z 为 0.当有两个或两个以上的温度探测器输出 1 时，总控制 器输出 1 信号，自动控制调整设备，使温度下降到 60℃以下。试写出总控制器真值表和逻 辑表达式。 解
十进制数码 6421 码
6311 码
4321 码
0
0000
0000
0000
1
0001
0001
0001

数字电路与系统设计第2章习题答案

数字电路与系统设计第2章习题答案

有A、B、C三个输入信号，试列出下列问题的真值表，并写出最小项表达式∑m（）。

（1）如果A、B、C均为0或其中一个信号为1时。

输出F=1，其余情况下F=0。

（2）若A、B、C出现奇数个0时输出为1，其余情况输出为0。

（3）若A、B、C有两个或两个以上为1时，输出为1，其余情况下，输出为0。

解：F1(A,B,C)=∑m（0，1，2，4）F2(A,B,C)=∑m（0，3，5，6）F3(A,B,C)=∑m（3，5，6，7）试用真值表证明下列等式：（1）AB+BC+AC=ABC+ABC（2）AB+BC+AC=AB BC AC证明：（1）真值表相同，所以等式成立。

（2）略对下列函数，说明对输入变量的哪些取值组合其输出为1（1）F（A,B,C）=AB+BC+AC（2）F（A,B,C）=(A+B+C)(A+B+C)（3）F（A,B,C）=(AB+BC+AC)AC解：本题可用真值表、化成最小项表达式、卡诺图等多种方法求解。

（1）F输出1的取值组合为：011、101、110、111。

（2）F输出1的取值组合为：001、010、011、100、101、110。

（3）F输出1的取值组合为：101。

试直接写出下列各式的反演式和对偶式。

(1)F(A,B,C,D,E)=[(AB+C)·D+E]·B(2) F(A,B,C,D,E)=AB+CD+BC+D+CE+B+E(3) F(A,B,C)=AB+C AB C解：(1) F=[(A+B)·C+D]·E+BF'=[(A+B)·C+D]·E+B(2) F=(A+B)(C+D)·(B+C)·D·(C+E)·B·EF'=(A+B)(C+D)·(B+C)·D·(C+E)·B·E(3)F=(A+B)·C+ A+B+CF'=(A+B)·C+A+B+C用公式证明下列等式：(1)AC+AB+BC+ACD=A+BC(2)AB+AC+(B+C) D=AB+AC+D(3)BCD+BCD+ACD+ABCD+ABCD+BCD+BCD=BC+BC+BD(4)ABC+BC+BCD+ABD=A + B +C+D证明：略已知ab+ab=ab,ab+ab=ab,证明：（1）abc=abc（2）abc=abc证明：略试证明：（1）若ab+ a b=0则a x+b y=ax + by（2）若a b+ab=c，则a c + ac=b证明：略将下列函数展开成最小项之和：（1）F（ABC）=A+BC（2）F（ABCD）=（B+C）D+(A+B) C（3）F(ABC)=A+B+C+A+B+C解：（1）F（ABC）=∑m(3,4,5,6)(2) F（ABCD）=∑m(1,3,5,6,7,9,13,14,15)(3) F(ABC)=∑m(0,2,6)将题中各题写成最大项表达式，并将结果与题结果进行比较。

人邮社数字电路逻辑设计习题答案

人邮社数字电路逻辑设计习题答案
9．将下列十进制数转换成二进制数、八进制数和十六进制数（精确
到二进制小数点后4位）。 答案：（1）（1000001）2
（2）（0.0100）2，
（3）（100001.0101）2 10．写出下列各数的原码、 答案：（1）原码=反码=补码=0.1011
（2）原码=1.1100， 反码=1.0011，补码=1.0100（3）原码=110110，反码=101001，补码=101010
7．按二进制运算法则计算下列各式。
答案：（1）110001（2）110.11（3）10000111（4）101 8．将下列二进制数转换成十进制数、八进制（2）（0.8281）10， （0.65）8，
（3）（23.25）10， （27.2）8，
5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什
么？
答案：两个余3码表示的十进制数相加时，对运算结果修正的方 法是：如果有进位，则结果加3；如果无进位，则结果减3。为了解 决四位二进制运算高位产生的进位与一位十进制运算产生的进位之 间的差值。
6．奇偶检验码有哪些优点和不足？ 答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电 路也简单。缺点是只有检错能力，没有纠错能力，其次只能发现单错， 不能发现双错。
理和规则十分熟练时化简比较方便；缺点是没有固定的规律和步骤， 技巧性强，且通常难以判断化简结果是否达到了最简单。9．用卡诺图化简逻辑函数时，应如何画卡诺圈才能求得一个函数的 最简与—或表达式？
答案：注意两点： 第一，在覆盖所有1方格的前提下，卡诺圈的 个数应达到最少；第二，在满足合并规律的前提下，每个卡诺圈的大 小应达到最大。
11.已知［N］补=1.0110，求［N］原，［N］反和N。
答案：［N］原码=1.1010,［N］反码=1.0101,N= -0.1010

数字电子技术基础 第02章门电路习题解

数字电子技术基础 第02章门电路习题解

& & &
2.8
试比较TTL电路和CMOS电路的优、缺点。
解 CMOS门电路具有电路结构简单、功耗低、集成度高、抗 干扰能力强；工作速度较慢 TTL门电路工作速度快；功耗高、集成度较低、抗干扰能 力较弱
2.9 试说明下列各种门电路中哪些的输出端可以并联使用。 (1)具有推拉式输出级的TTL门电路； (2)TTL电路的OC门； (3)TTL电路的三态输出门； (4)普通的CMOS门： (5)漏极开路的CMOS门； (6)CMOS电路的三态输出门。
解:TTL输入标准值 UIH=2V (1)以基本TTL与非门为例,当输入端悬空时,T1和射极电流 iE1=0,集电极正偏,T2,T5饱和导通,相当于输入高电平情况,即 等效逻辑1 (2)uI>2V=UIH,所以为逻辑1 (3)uI>3.6V>2V=UIH,所以为逻辑1
2.4 指出图2.43中各门电路的输出是什么状态(高电平、低电平或高阻 态)。假定它们都是T1000系列的TTL门电路。 U & Y
逻辑门电路习题开关特性ttl门oc门综合mos21在图242所示各电路中当输入电压u分别为0v5v悬空时试计算输出电压u010202051102v假设成立u50751084ma1007200535maibsc10032300162mabsct饱和导通10v假设成立uuiuo2k3020k51k20k51k07v5v10va121010202051102v假设成立u50751084ma1007200535maibsc10032300162mabsct饱和导通10v假设成立uuiuo2k18k47k20k51k07v5v10vb122为什么说ttl与非门输入端在以下三种接法时在逻辑上都属于输入为0

数字逻辑与数字系统设计习题参考答案

数字逻辑与数字系统设计习题参考答案
[-87+12]补=10101001+00001100=10110101，-125+79=(-1001011)2=-75
2.3解：根据逻辑图可直接写出逻辑表达式：(a) F= ；(b) F=
解：设3个输入变量分别为A、B、C，输出为F，按题意，其中有奇数个为1，则输出F＝1，因此可写出其逻辑表达式为F= 。根据逻辑表达式可绘制逻辑习题2.3图如下：
习题2.3图
2.4解：根据逻辑图可直接写出逻辑表达式：(a) F= ；(b) F=
2.5解：
(1)若A+B=A+C,则B=C
不正确。若A=1，B和C为不同值（如B＝0，C＝1或B＝1，C＝0），A+B=A+C仍然成立。
(2)若AB=BC,则A=C
不正确。若B=0，A和C为不同值，等式仍然成立。
(3)若1+A=B,则A+AB=B
1.6(1)(117)8=(1001111)2=(79)10
(2)(7456)8=(111100101110)2=(3886)10
(3)(23765.64)8=(10 0111 1111 0101.1101)2=(10229.8125)10
(4)(0.746)8=(0.11111)2=(0.96875)10
W=A+BD+BCX= Y= Z=
= = = =
根据化简并变换后的逻辑表达式可绘制逻辑习题4-12图所示下：
4.13解：
//4.6的VerilogHDL描述
module ex6(a,b,s,f);//
input a,b,s;
output f;
assign f=(s?b:a);
endmodule
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

IoH 0.5mA = ≈ 167 IiH 3 × 1uA IoH 0.5mA = ≈ 167 IiH 3 × 1uA
由 CMOS 的与非门电路可以得到，当与非门的 3 个输入端并接到高电平时，三个串接的 NMOS 管导通，而三个并接的 PMOS 管都截止，所以其输入高电平总电流为 3×IiH， n = 2）当非们输出为低电平时： 由 CMOS 的或非门电路可以得到，当或非门的 3 个输入端并接到低电平时，三个并接的 NMOS 管都截止，而三个串接的 PMOS 管导通，所以其输入低电平总电流为 3×IiL， n =
题图 2-7 答案：不能 2-8 由 CMOS 门组成的电路如题图 2-8 所示。已知 VDD =5V，VOH ≥3.5Ｖ，VOL ≤0.5Ｖ。门的驱动能力 IO=±4mA。问某人根据给定电路写出的输出表达式是否正确？
题图 2-8 (a) F1 = AB • CD 2-9 正确 (b) F2 =AB+CD 正确 (c) F3 =AB+CD 不正确
题图 2-5
∴ RL ≤
答案：①输出为高电平时：
′ − VOH (min) VCC nI OH + mI IH
(n = 2, m = 8)
=
5−3 = 3.2k 2*0.15 + 8*0.04
RL ≥
②当输出为低电平：
′ − VOL VCC (m ' = 6) I LM − m′I IL 5 − 0.3 = 0.47 K 16 − 6 ×1
RP (V − v BE 1 ) RP + R1 CC
0.1 (5 − 0.7) = 0.14V = 0.1 + 3
vI2= vI1 =0.14V
（5）vI1 经 10K 电阻接地 2-3
vI2=1.4V
已知 TTL 门的参数是 VOH=3.5V, VOL=0.1V, VIHmin=2.4V, VILmax =0.3V, IIH=20μA, IIS=1.0mA,
CMOS 门电路如题图 2-9 所示,分析此电路所完成的逻辑功能。
VDD C B A F
答案： F = A + B + C 题图 2-9 2-10 逻辑门电路如题图 2-10 所示，针对下面两种情况，分别讨论它们的输出与输入各是什么关系？ 两个电路均为 CMOS 电路输出高电平 5V，输出低电平 0V。 答案： F1 = A; F 2 = 1 两个电路均为 TTL 电路输出高电平 3.6V，输出低电平 0.3V，门电路的开门电阻为 2KΩ ，关门电阻 为 0.8kΩ 。 答案： F1 = A; F 2 = A
=
选 RL=1K
2-6 已知题图 2-6 中各个门电路都是 74H 系列 TTL 电路，试写出各门电路的输出状态（0，1 或 Z）
Vcc ViH NO_ INPUT
&
Y1
ViL
≥1
ViH Y2
&
Y3
0
≥1
Vcc ViL EN=1
1
10K
0
ViL
Y4
& Y5
Vcc
1K
=1
Y6
100
1
1
0
题图 2-6 2-7 已知 TTL 三态门电路及控制信号 C1 ， C2 的波形如题图 2-7 所示，试分析此电路能否正3 ×1uA
由 CMOS 的与非门电路可以得到，当与非门的 3 个输入端并接到低电平时，三个串接的 NMOS 管都截止，而三个并接的 PMOS 管导通，所以其输入低电平总电流为 3×IiL， n =
IoL 0.5mA = ≈ 167 IiL 3 ×1uA
总结以上结果，对电路（a）能够驱动 167 个三输入端或非门，对电路（b）能够驱动 167 个三输入端 与非门。
图 2-5 中的 RL 选择合适的阻值，已知 OC 门输出管截止时的漏电流为 IOH=150μA，输出管导通时允 许的最大负载电流为 ILM=16mA； 负载门的低电平输入电流为 IIL=1mA， 高电平输入电流为 IIH=40μA， V'CC=5V，要求 OC 门的输出高电平 VOH≧3.0V，输出低电平 VOL≦0.3V。
题图 2－13 答案： Y 1 = A ； Y 2 = AB ； Y 3 = A, Y 3 = A ; Y4 不能; Y 5 = AB • CD
'
Y6 不能； Y 7 = E AB + ECD ; Y8 不能 ； Y 9 = EA + EB ;Y10 不能 2-14 试分别画出实现逻辑函数 F1 = AC + BD + E ; F 2 = ( A + B) D + C 的 CMOS 电路图。 答案：
V CC R1 3k
v I1 v I2
V
& &
v I1 v I2
vB1 T1 100 100K
be 2 be 5
题图 2-2 答案：（1） vI1 悬空 vI2=1.4V （2）vI1=0.2V vI2=0.2V （3） vI1＝3.2V vI2=1.4V
vI 1 =
（4）vI1 经 100Ω 电阻接地；
2-1 已知门电路及重复频率为 100MHZ 的输入信号如题图 2-1 所示。试补画出下列两种情况下的输出 信号波形。 (1) 不考虑非门的延迟时间； (2) 设非门、与非门的延迟时间均为 t PD =10ns.
答案：
Vi
t Vo1 10ns 20ns
Vo2
2-2 试说明在下列情况下， 用万用表测量题图 2-2 中 vI2 得到的电压各为多少？与非门为 74H 系列 TTL 电路，万用表使用 5V 量程，内阻为 20KΩ/V。vI1 悬空；（2）vI1=0.2V；（3）vI1=3.2V；(4) vI1 经 100Ω 电阻接地；（5）vI1 经 10K 电阻接地。
VDD
B A E C D E A B C A D C B A
VDD
D
F1
VDD
F2
D
B
2-15 设 CMOS 门电路参数为 IOH＝0.5mA，IOL＝0.5mA，IiH=1uA，IiL＝1uA，试问题图 2-15 能够驱动 门的个数。
≥1
& 1
1
≥1
& (a)
题图 2 － 15
(b)
答案：1）当非们输出为高电平时： 由 CMOS 的或非门电路可以得到，当或非门的 3 个输入端并接到高电平时，三个并接的 NMOS 管导通，而三个串接的 PMOS 管都截止，所以其输入高电平总电流为 3×IiH， n =
A B
100Ω ≥1
A F1 B
& F2
10K
(a) 题图 2-10 2-11 CMOS 门电路如题图 2-11 所示，试写出各门的输出电平。
(b)
题图 2-11 答案：（a）VDD （b）0 （c）0 2-12 CMOS 与或非门不使用的输入端应如何连接？ 答案：当在一起的两个输入端都不使用时，它们同时接地； 当在一起的两个输入端只有一个不使用时，它通过电阻接电源。 2-13 分析题图 2-13 所示各 CMOS 门电路，哪些能正常工作，哪些不能。写出能正常工作的输出信号 的逻辑表达式。
IOH=360μA, IOL=8mA, 求题图 2-3 中 R 的取值范围.
1
A
G1
R
&
1
F1
G2
A
G1 R
≥1
G2
F2
(a) 题图 2-3 答：图(a)：
(b)
G2 输入端相当于接对地(VOL=0.1V)电阻 R， 其输入端电压 VI2=VOL+IIS×R， (1) G1 输出低电平 VOL 时， 为保证逻辑关系正确，需满足 VI2≤VILmax，故 R ≤ (VILmax - VOL )/IIS=(0.3-0.1)/1.0=0.2 kΩ (2) G1 输出高电平 VOH 时，流入 G2 输入端的电流为 IIH×3=60μA，为保证逻辑关系正确，需满足 VI2≥VIHmin，即 VOH-IIH×3×R ≥ VIHmin，故 R ≤ (VOH – VIHmin)/(IIH×3)=(3.5-2.4)/0.06 ≈18.3 kΩ ∴R ≤0.2 kΩ 图(b)： (1) G1 输出高电平 VOH 时，流入或非门 G2 输入端的电流为 IIH×3=60μA，流过电阻 R 的最大电流 为 VOH/R，为保证逻辑关系正确，需满足 IOH ≥ IR+IIH×3=VOH/R+ IIH×3，故 R ≥ VOH/( IOH-IIH×3)=3.5/(0.36-0.02×3) ≈ 11.67kΩ (2) G1 输出低电平时，对 R 无要求。 ∴R≥11.67 kΩ 2-4 在 STTL 集成电路中，采取了哪些措施来提高电路的开关速度？ 试为题 改进措施：在 74H 系列的基础上 ①采用抗饱和三极管提高速度，②采用有源泻放回路 2-5