第二章习题解答

习题解答(第二章)一、选择题1．25℃时，0.01mol/kg的糖水的渗透压为π1，而0.01 mol/kg的尿素水溶液的渗透压π2，则___ B _。

（A）π1＜π2（B）π1 =π2（C）π1＞π2（D）无法确定2．应用克-克方程回答问题：当物质由固相变为气相时，平衡压力随温度降低而__ C__。

（A）不变（B）升高（C）降低（D）视不同物质升高或降低3．通常称为表面活性剂的物质，是指当其加入少量后就能__ C的物质。

（A）增加溶液的表面张力（B）改变溶液的导电能力（C）显著降低溶液的表面张力（D）使溶液表面发生负吸附4．兰格缪尔（Langmuir）等温吸附理论中最重要的基本假设是_ D___。

（A）气体为理想气体（B）多分子层吸附（C）固体表面各吸附位置上的吸附能力是不同的（D）单分子层吸附5．溶胶的基本特征之一是___D__。

（A）热力学上和动力学上皆稳定的系统（B）热力学上和动力学上皆不稳定的系统（C）热力学上稳定而动力学上不稳定的系统（D）热力学上不稳定而动力学上稳定的系统6．下列各性质中，属于溶胶的动力学性质的是___A___。

（A）布朗运动（B）电泳（C）丁达尔现象（D）流动电势7．引起溶胶聚沉的诸因素中，最重要的是___D__。

（A）温度的变化（B）溶胶浓度的变化（C）非电解质的影响（D）电解质的影响8．用KBr加入浓的AgNO3溶液中，制备得AgBr溶胶，再向其中加入下列不同的电解质，能使它在一定时间内完全聚沉所需电解质最少的是__ C _。

（A）Na2SO4（B）NaNO3 （C）K3[Fe(CN)6] （D）KCl9．等体积0.10mol/dm3 KI和0.12mol/dm3的AgNO3溶液混合制成的AgI溶胶，下列电解质中，聚沉能力最强的是___D__。

（A ）Na 2SO 4 （B ）MgSO 4 （C ）K 3[Fe(CN)6] （D ）FeCl 3二、简答题1．理想气体存在吗？真实气体的pVT 行为在何种条件下可用pV=nRT 来描述？答：事实上，理想气体不存在。

《土力学》第二章习题集及详细解答第2章土的物理性质及分类一填空题1.粘性土中含水量不同，可分别处于、、、、四种不同的状态。

其界限含水量依次是、、。

2.对砂土密实度的判别一般采用以下三种方法、、。

3.土的天然密度、土粒相对密度、含水量由室内试验直接测定，其测定方法分别是、、。

4. 粘性土的不同状态的分界含水量液限、塑限、缩限分别用、、测定。

5. 土的触变性是指。

6.土的灵敏度越高，其结构性越强，受扰动后土的强度降低越。

7. 作为建筑地基的土，可分为岩石、碎石土砂土、、粘性土和人工填土。

8.碎石土是指粒径大于 mm的颗粒超过总重量50%的土。

9.土的饱和度为土中被水充满的孔隙与孔隙之比。

10. 液性指数是用来衡量粘性土的状态。

二、选择题1．作为填土工程的土料，压实效果与不均匀系数C u的关系：( )（A）C u大比C u小好(B) C u小比C u大好(C) C u与压实效果无关2.有三个同一种类土样，它们的含水率都相同，但是饱和度S r不同，饱和度S r越大的土，其压缩性有何变化？( )(A)压缩性越大(B) 压缩性越小(C) 压缩性不变3.有一非饱和土样，在荷载作用下，饱和度由80%增加至95%。

试问土样的重度γ和含水率怎样改变？( )(A)γ增加，减小(B) γ不变，不变(C)γ增加，增加4.土的液限是指土进入流动状态时的含水率，下述说法哪种是对的？( )(A)天然土的含水率最大不超过液限(B) 液限一定是天然土的饱和含水率(C)天然土的含水率可以超过液限，所以液限不一定是天然土的饱和含水率5. 已知砂土的天然孔隙比为e＝0.303，最大孔隙比e max＝0.762，最小孔隙比e min＝0.114，则该砂土处于( )状态。

（A）密实（B）中密 (C)松散（D）稍密6．已知某种土的密度ρ＝1.8g/cm3，土粒相对密度ds＝2.70，土的含水量w＝18.0％，则每立方土体中气相体积为( )(A)0.486m3 (B)0.77m3(C)0.16m3(D)0.284m37.在土的三相比例指标中，直接通过室内试验测定的是（）。

第二章习题答案2.1.1 质点的运动学方程为j t i t r j i t r ˆ)14(ˆ)32()2(ˆ5ˆ)23()1(-+-=++=求质点的轨迹并用图表示解：（1）⎭⎬⎫=+=523y t x 平行于x 轴的直线：y=5(2)⎭⎬⎫-=-=1432t y t x 消去t 的轨迹方程：0534=-+y x2.1.2 质点的运动学方程为kj e i e r t t ˆ2ˆˆ22++=-。

(1)求质点的轨迹。

（2）求自t = -1 至t = 1质点的位移解：（1）由运动方程得质点轨迹的参数方程为 )3()2()1(222⎪⎩⎪⎨⎧===-z ey e x tt （1）x （2）消去t ，得轨迹方程 ⎩⎨⎧==21z xy（2）自t = -1 至t = 1质点的位移：je e i e e r r r k j e i e r k j e i e r t t ˆ)(ˆ)(ˆ2ˆˆˆ2ˆˆ,1,1222211221221-------+-=-=∆++=++==-= 2.1.3 质点的运动学方程为j t i t r ˆ)32(ˆ42++=。

（1）求质点的轨迹；（2）求自t=0至t=1质点的位移解：由质点的运动方程⎩⎨⎧+==)2(32)1(42t y t x （1） 质点的轨迹：消去t 得：2)3(-=y x（2） 位移：ji r r r j i r j r t t ˆ2ˆ4ˆ5ˆ4ˆ3101221+=-=∆+====2.2.1 雷达站于某瞬时测得飞机位置为R 1=4100m ，θ1=33.70，0.75s 后测得R 2=4240m ，θ2=29.30，R 1,R 2均在铅直平面内，求飞机瞬时速度的近似值和飞行方向（α角）。

解：取雷达站位置为原点，飞机在两个时刻的位置矢量分别为r 1和r 2，则| r 1|=R 1, | r 2|=R 2，如图所示由余弦定理，在0.75s 时间间隔内飞机的位移的大小为mR R R R r r r r r 4.349)3.297.33cos(42404100242404100)cos(2)cos(200222121222121212221≈-⨯⨯-+=--+=--+=∆θθθθ飞机的瞬时速度的大小：==∆∆≈smt r v 75.04.349465.8m/s飞机的瞬时速度方向：由正弦定理)3.297.33sin(4.349sin 4240)sin(sin 00212-=⇒-∆=γθθγr r100001207.341806.11193.0arcsin 18090,93.04.4sin 4.3494240sin ≈--=∴≈-=∴>∴>≈=γθαγγγr r另解：利用矢量在直角坐标系中的正交分解. 选平面直角坐标系,取雷达站的位置为坐标原点,x 轴沿水平方向,y 轴铅直向上,则在两个时刻飞机的位置矢量分别可表示为ji j i jR i R r ji j i jR i R r ˆ98.2074ˆ57.3697ˆ3.29sin 4240ˆ3.29cos 4240ˆsin ˆcos ˆ86.2274ˆ01.3411ˆ7.33sin 4100ˆ7.33cos 4100ˆsin ˆcos 00222220011111+=⨯+⨯=+=+=⨯+⨯=+=θθθθ 飞机飞行0.75s 后的位移矢量为j i r r r ˆ88.199ˆ56.28612-=-=∆飞机瞬时速度的大小的近似值:s m t rv /8.46575.038.34975.088.19956.28622=≅+=∆∆≈飞机瞬时速度的方向与x 轴的夹角:09.3482.038.34956.286ˆcos =∴==∆⋅∆=ααr i r2.2.2 一圆柱体沿抛物线轨道运动.抛物线的轨道方程为y=x 2/200(长度:mm).第一次观测到圆柱体在x=249mm 处,经过时间2ms 后圆柱体移到x=234mm 处.求圆柱体瞬时速度的近似解：第一次观测时，x=249mm, y=x 2/200=(249)2/200≈310mm ，j i r ˆ310ˆ2491+=2ms 后，x=234mm, y=x 2/200=(234)2/200≈273.78mm ，j i r ˆ78.273ˆ2342+=圆柱体的位移：mm r j i r r r 2.3922.3615ˆ22.36ˆ152212≈+=∆--=-=∆∴ms mm msmm t r v /6.1922.39==∆∆≈速度与x 轴的夹角：5.112383.02.3915ˆcos -≈∴-≈-=∆⋅∆=ααr i r2.2.3 一人在北京音乐厅内听音乐，离演奏着17m 。

2.1设有12枚同值硬币，其中一枚为假币。

只知道假币的重量与真币的重量不同，但不知究竟是重还是轻。

现用比较天平左右两边轻重的方法来测量（因无砝码）。

为了在天平上称出哪一枚是假币，试问至少必须称多少次？解：分三组，每组4个，任意取两组称。

会有两种情况，平衡，或不平衡。

(1) 平衡：明确假币在其余的4个里面。

从这4个里面任意取3个，并从其余8个好的里面也取3个称。

又有 两种情况：平衡或不平衡。

a ）平衡：称一下那个剩下的就行了。

b ）不平衡：我们至少知道那组假币是轻还是重。

从这三个有假币的组里任意选两个称一下，又有两种情况：平衡与不平衡，不过我们已经知道假币的轻重情况了，自然的，不平衡直接就知道谁是假币；平衡的话，剩下的呢个自然是假币，并且我们也知道他是轻还是重。

(2) 不平衡：假定已经确定该组里有假币时候：推论1：在知道该组是轻还是重的时候，只称一次，能找出假币的话，那么这组的个数不超过3。

我们知道，只要我们知道了该组（3个）有假币，并且知道轻重，只要称一次就可以找出来假币了。

从不平衡的两组中，比如轻的一组里分为3和1表示为“轻（3）”和“轻（1）”，同样重的一组也是分成3和1标示为“重（3）”和“重（1）”。

在从另外4个剩下的，也就是好的一组里取3个表示为“准（3）”。

交叉组合为：轻（3） + 重（1） ？=======？ 轻（1） + 准（3）来称一下。

又会有3种情况：(1)左面轻：这说明假币一定在第一次称的时候的轻的一组，因为“重（1）”也出现在现在轻的一边，我们已经知道，假币是轻的。

那么假币在轻（3）里面，根据推论1，再称一次就可以了。

(2)右面轻：这里有两种可能：“重（1）”是假币，它是重的，或者“轻（1）”是假币，它是轻的。

这两种情况，任意 取这两个中的一个和一个真币称一下即可。

(3)平衡：假币在“重（3）”里面，而且是重的。

根据推论也只要称一次即可。

2.2 同时扔一对骰子，当得知“两骰子面朝上点数之和为2”或“面朝上点数之和为8”或“骰子面朝上之和是3和4”时，试问这三种情况分别获得多少信息量？解：设“两骰子面朝上点数之和为2”为事件A ，则在可能出现的36种可能中，只能个骰子都为1，这一种结果。

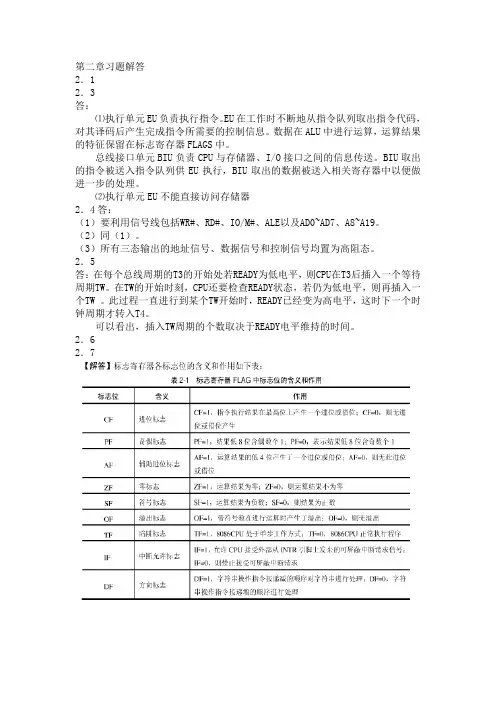
第二章习题解答2．12．3答：⑴执行单元EU负责执行指令。

EU在工作时不断地从指令队列取出指令代码，对其译码后产生完成指令所需要的控制信息。

数据在ALU中进行运算，运算结果的特征保留在标志寄存器FLAGS中。

总线接口单元BIU负责CPU与存储器、I/O接口之间的信息传送。

BIU取出的指令被送入指令队列供EU执行，BIU取出的数据被送入相关寄存器中以便做进一步的处理。

⑵执行单元EU不能直接访问存储器2．4答：（1）要利用信号线包括WR#、RD#、IO/M#、ALE以及AD0~AD7、A8~A19。

（2）同（1）。

（3）所有三态输出的地址信号、数据信号和控制信号均置为高阻态。

2．5答：在每个总线周期的T3的开始处若READY为低电平，则CPU在T3后插入一个等待周期TW。

在TW的开始时刻，CPU还要检查READY状态，若仍为低电平，则再插入一个TW 。

此过程一直进行到某个TW开始时，READY已经变为高电平，这时下一个时钟周期才转入T4。

可以看出，插入TW周期的个数取决于READY电平维持的时间。

2．62．72．8通用寄存器包含以下8个寄存器：AX、BX、CX和DX寄存器一般用于存放参与运算的数据或运算的结果。

除此之外：AX：主要存放算术逻辑运算中的操作数，以及存放I/O操作的数据。

BX：存放访问内存时的基地址。

CX：在循环和串操作指令中用作计数器。

DX：在寄存器间接寻址的I/O指令中存放I/O地址。

在做双字长乘除法运算时，DX 与AX合起来存放一个双字长数。

SP：存放栈顶偏移地址。

BP：存放访问内存时的基地址。

SP和BP也可以存放数据，但它们的默认段寄存器都是SS。

SI：常在变址寻址方式中作为源地址指针。

DI：常在变址寻址方式中作为目标地址指针。

专用寄存器包括4个段寄存器：CS：代码段寄存器，用于存放代码段的段基地址。

DS：数据段寄存器，用于存放数据段的段基地址。

SS：堆栈段寄存器，用于存放堆栈段的段基地址。

第二章 随机变量及其分布I 教学基本要求1、了解随机变量的概念以及它与事件的联系；2、理解随机变量的分布函数的概念与性质；理解离散型随机变量的分布列、连续型随机变量的密度函数及它们的性质；3、掌握几种常用的重要分布：两点分布、二项分布、泊松分布、均匀分布、指数分布、正态分布，且能熟练运用；4、会求简单随机变量函数的分布.II 习题解答A 组1、检查两个产品，用T 表示合格品，F 表示不合格品，则样本空间中的四个样本点为1(,)F F ω=、2(,)T F ω=、3(,)F T ω=、4(,)T T ω=以X 表示两个产品中的合格品数.(1) 写出X 与样本点之间的对应关系；(2) 若此产品的合格品率为p ，求(1)p X =？ 解：(1)10ω→、21ω→、31ω→、42ω→；(2) 12(1)(1)2(1)p X C p p p p ==-=-.2、下列函数是否是某个随机变量的分布函数？(1) 021()2021x F x x x <-⎧⎪⎪=-≤<⎨⎪≥⎪⎩； (2) 21()1F x x =+ ()x -∞<<+∞. 解：(1) 显然()F x 是单调不减函数；0()1F x ≤≤，且()0F -∞=、()1F +∞=；(0)()F x F x +=，故()F x 是某个随机变量的分布函数.(2) 由于()01F +∞=≠，故()F x 不是某个随机变量的分布函数. 3、设X 的分布函数为(1)0()00x A e x F x x -⎧-≥=⎨<⎩求常数A 及(13)p X <≤？解：由()1F +∞=和lim (1)xx A e A -→+∞-=得1A =；(13)(3)(1)(3)(1)p X p X p X F F <≤=≤-≤=-3113(1)(1)e e e e ----=---=-.4、设随机变量X 的分布函数为200()0111x F x Ax x x ≤⎧⎪=<≤⎨⎪>⎩求常数A 及(0.50.8)p X <≤？解：由(10)(1)F F +=得1A =；(0.50.8)(0.8)(0.5)(0.8)(0.5)p X p X p X F F <≤=≤-≤=- 220.80.50.39=-=.5、设随机变量X 的分布列为()ap X k N==(1,2,,)k N = 求常数a ？解：由11ii p+∞==∑得11Nk a N ==∑ 1a ⇒=.6、一批产品共有100个，其中有10个次品，求任意取出的5个产品中次品数的分布列？ 解：设X 表示5个产品中的次品数，则X 是离散型随机变量，其所有可能取值为0、1、…、5，且0510905100(0)C C p X C ==、1410905100(1)C C p X C ==、2310905100(2)C C p X C ==、3210905100(3)C C p X C ==、4110905100(4)C C p X C ==、5010905100(5)C C p X C ==于是X 的分布列为510905100()k k C C p X k C -== (0,1,,5k =. 7、设10件产品中有2件次品，进行连续无放回抽样，直至取到正品为止，以X 表示抽样次数，求(1) X 的分布列； (2) X 的分布函数？解：(1) 由题意知X 是离散型随机变量，其所有可能取值为1、2、3，且84(1)105p X ===、288(2)10945p X ==⨯=、2181(3)109845p X ==⨯⨯= 于是X 的分布列为(2) 由(1)可知的分布函数为014125()44234513x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩.8、设随机变量X 的分布函数为010.211()0.3120.52313x x F x x x x <-⎧⎪-≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩ 求X 的分布列？解：X 90.1，求在同一时刻(1) 恰有2个设备被使用的概率； (2) 至少有3个设备被使用的概率； (3) 至多有3个设备被使用的概率？解：设X 表示被同时使用的供水设备数，则~(5,0.1)X b (1) 恰有2个设备被使用的概率为2235(2)(0.1)(0.9)0.0729p X C ===；(2) 至少有3个设备被使用的概率为(3)(3)(4)(5)p X p X p X p X ≥==+=+=33244550555(0.1)(0.9)(0.1)(0.9)(0.1)(0.9)0.00856C C C =++=；(3) 至多有3个设备被使用的概率为(3)1(4)(5)p X p X p X ≤=-=-=44550551(0.1)(0.9)(0.1)(0.9)0.99954C C =--=.10、经验表明：预定餐厅座位而不来就餐的顾客比例为20%，如今餐厅有50个座位，但预定给了52位顾客，求到时顾客来到餐厅而没有座位的概率是多少？解：设X 表示预定的52位顾客中不来就餐的顾客数，则~(52,0.2)X b ，由于“顾客来到餐厅没有座位”等价于“52位顾客中至多有1位不来就餐”，于是所求概率为005211515252(1)(0)(1)(0.2)(0.8)(0.2)(0.8)p X p X p X C C ≤==+==+0.0001279=.11、设某城市在一周内发生交通事故的次数服从参数为0.3的泊松分布，求 (1) 在一周内恰好发生2次交通事故的概率； (2) 在一周内至少发生1次交通事故的概率？解：设X 表示该城市一周内发生交通事故的次数，则~(0.3)X P (1) 在一周内恰好发生2次交通事故的概率20.30.3(2)0.03332!p X e -===；(2) 在一周内至少发生1次交通事故的概率00.30.3(1)1(0)10.2590!p X P X e -≥=-==-=.12、设X 服从泊松分布，已知(1)(2)p X p X ===，求(4)p X =？ 解：由(1)(2)p X p X ===得22ee λλλλ--=2λ⇒=422(4)0.09024!p X e -⇒===.13、一批产品的不合格品率为0.02，现从中任取40件进行检查，若发现两件或两件以上不合格品就拒收这批产品，分别用以下方法求拒收的概率：(1) 用二项分布作精确计算；(2) 用泊松分布作的似计算？解：设X 表示抽取的40件产品中的不合格品数，则~(40,0.02)X b (1) 拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-=0040113940401(0.02)(0.98)(0.02)(0.98)0.1905C C =--=；(2) 由于400.020.8λ=⨯=，于是拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-= 0.80.810.80.1912e e --≈--=.14、设随机变量X 的密度函数为201()0x x f x ≤≤⎧=⎨⎩其它求X 的分布函数？解：由()()xF x f t dt -∞=⎰得当0x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当01x ≤≤时2200()()02|xxxF x f t dt dt tdt t x -∞-∞==+==⎰⎰⎰当1x >时0121001()()020|1xxF x f t dt dt tdt dt t -∞-∞==++==⎰⎰⎰⎰于是所求分布函数为20()0111x F x x x x <⎧⎪=≤≤⎨⎪>⎩. 15、设随机变量X 的密度函数为212(1)12()0x f x x ⎧-≤≤⎪=⎨⎪⎩其它求X 的分布函数？解：由()()xF x f t dt -∞=⎰得当1x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当12x ≤≤时1121111()()02(1)2()|2(2)x xx F x f t dt dt dt t x t t x-∞-∞==+-=+=+-⎰⎰⎰ 当2x >时122121211()()02(1)02()|1xx F x f t dt dt dt dt t t t-∞-∞==+-+=+=⎰⎰⎰⎰于是所求分布函数为011()2(2)1212x F x x x x x <⎧⎪⎪=+-≤≤⎨⎪>⎪⎩. 16、设随机变量X 的密度函数为cos ()220A x x f x ππ⎧-≤≤⎪=⎨⎪⎩其它求(1) 常数A ；(2) X 的分布函数；(3) (0)4p X π<≤？解：(1) 由()1f x dx +∞-∞=⎰得2222220cos 0sin |21dt A xdx dt A x A ππππππ-+∞--∞-++===⎰⎰⎰12A ⇒=； (2) 当2x π<-时()()00xxF x f t dt dt -∞-∞===⎰⎰当22x ππ-≤≤时221111()()0cos sin |sin 2222x xx F x f t dt dt tdt t x πππ---∞-∞-==+==+⎰⎰⎰当2x π>时22222211()()0cos 0sin |122xx F x f t dt dt tdt dt t ππππππ---∞-∞-==++==⎰⎰⎰⎰ 于是所求分布函数为0211()sin 222212x F x x x x ππππ⎧<-⎪⎪⎪=+-≤≤⎨⎪⎪>⎪⎩；(3) (0)()(0)()(0)444p X p X p X F F πππ<≤=≤-≤=-1111sin sin 024222π=+--=17、设随机变量X 的分布函数为1()ln 11x F x xx e x e<⎧⎪=≤≤⎨⎪>⎩求(1) (03)p X <≤、(2)p X <、(2 2.5)p X <<；(2) X 的密度函数？解：(1) (03)(3)(0)(3)(0)101p X p X p X F F <≤=≤-≤=-=-=(2)(2)(2)(2)ln 2p X p X p X F <=≤-===5(2 2.5)(2 2.5)(2.5)(2)ln 2.5ln 2ln 4p X p X F F <<=<≤=-=-=；(2) 由于在()F x 的可导点处，有()()f x F x '=，于是X 的密度函数为11()0x ef x x⎧≤≤⎪=⎨⎪⎩其它.18、设~(1,6)K U ，求方程210x Kx ++=有实根的概率？ 解：由~(1,6)K U 得K 的密度函数为116()5k f k ⎧<<⎪=⎨⎪⎩其它又由于方程210x Kx ++=有实根等价于240K -≥，即||2K ≥，于是方程有实根的概率为22(||2)(2)(2)()()p K p K p K f k dk f k dk -+∞-∞≥=≤-+≥=+⎰⎰621455dk ==⎰. 19、调查表明某商店从早晨开始营业起直至第一个顾客到达的等待时间X (单位：分钟)服从参数为0.4的指数分布，求下述事件的概率(1) X 至多3分钟； (2) X 至少4分钟；(3) X 在3分钟至4分钟之间； (4) X 恰为3分钟？解：(1) X 至多3分钟的概率为0.43 1.2(3)(3)11p X F e e -⨯-≤==-=-；(2) X 至少4分钟的概率为0.44 1.6(4)1(4)1(4)1(1)p X p X F e e -⨯-≥=-<=-=--=；(3) X 在3分钟至4分钟之间的概率为(34)(4)(3)(4)(3)p X p X p X F F ≤≤=≤-<=-0.440.43 1.2 1.6(1)(1)e e e e -⨯-⨯--=---=-；(4) X 恰为3分钟的概率为(3)0p X ==.20、设~(0,1)X N ，求下列事件的概率( 2.35)p X ≤；( 1.24)p X ≤-；(|| 1.54)p X ≤？解：( 2.35)(2.35)0.9906p X ≤=Φ=；( 1.24)( 1.24)1(1.24)10.89250.1075p X ≤-=Φ-=-Φ=-=； (|| 1.54)( 1.54 1.54)(1.54)( 1.54)p X p X ≤=-≤≤=Φ-Φ- (1.54)[1(1.54)]2(1.54)120.938210.8764=Φ--Φ=Φ-=⨯-=.21、设~(3,4)X N ，(1) 求(25)p X <≤、(||2)p X >、(3)p X >；(2) 确定c ，使得()()p X c p X c >=≤；(3) 若d 满足()0.9p X d >≥，则d 至多为多少？解：(1) 23353(25)()222X p X p ---<≤=≤≤ (1)(0.5)(1)(0.5)10.84130.691510.5328=Φ-Φ-=Φ+Φ-=+-= 23323(||2)1(||2)1()222X p X p X p ---->=-≤=-≤≤1(0.5)( 2.5)1(0.5)(2.5)=-Φ-+Φ-=+Φ-Φ 10.69150.99380.6977=+-=333(3)1(3)1()22X p X p X p -->=-≤=-≤ 1(0)10.50.5=-Φ=-=；(2) 由()()p X c p X c >=≤得1()()p X c p X c -≤=≤ 3330.5()()()222X c c p X c p ---⇒=≤=≤=Φ 3032c c -⇒=⇒=； (3) 由()0.9p X d >≥得3330.9()1()1()1()222X d d p X d p X d p ---≤>=-≤=-≤=-Φ 33()0.11()0.122d d--⇒Φ≤⇒-Φ≤ 33()0.9 1.2820.43622d d d --⇒Φ≥⇒≥⇒≤.22、从甲地飞住乙地的航班，每天上午10:10起飞，飞行时间X 服从均值为4h ，标准差为20min 的正态分布.(1) 该航班在下午2:30以后到达乙地的概率； (2) 该航班在下午2:20以前到达乙地的概率；(3) 该航班在下午1:50至2:30之间到达乙地的概率？ 解：(1) 该航班在下午2:30以后到达乙地的概率为240260240240(260)()1(1)202020X X p X p p ---≥=≥=-< 1(1)10.84130.1587=-Φ=-=；(2) 该航班在下午2:20以前到达乙地的概率为240250240(250)()(0.5)0.69152020X p X p --≤=≤=Φ=； (3) 该航班在下午1:50至2:30之间到达乙地的概率为220240240260240(220260)()202020X p X p ---≤≤=≤≤(1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.23、某地抽样调查结果表明，考生的外语成绩(百分制)近似地服从2(72,)N σ，已知96分以上的人数占总数的2.3%，试求考生的成绩在60分至84分之间的概率？解：设考生的外语成绩为X ，则2~(72,)X N σ 由96分以上的人数占总数的2.3%得0.023(96)p X => 729672240.977(96)()()X p X p σσσ--⇒=≤=≤=Φ242σ⇒=12σ⇒=于是，考生的成绩在60分至84分之间的概率为6072728472(6084)()121212X p X p ---≤≤=≤≤ (1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.24求cos Y X =的分布列？解：由X于是Y25求2Y X =的分布列？解：由26、设随机变量的密度函数为2311()2X xx f x ⎧-<<⎪=⎨⎪⎩其它求随机变量3Y X =+的密度函数？解：由题意知，当2y ≤时，有()()0Y F y p Y y =≤=当24y <<时，有()()(3)(3)(3)Y X F y p Y y p X y p X y F y =≤=+≤=≤-=-当4y ≥时，有()()1Y F y p Y y =≤=即Y 的分布函数02()(3)2414Y X y F y F y y y ≤⎧⎪=-<<⎨⎪≥⎩于是，Y 的密度函数()()Y Y f y F y '=(3)240XF y y '-<<⎧=⎨⎩其它23(3)2420y y ⎧-<<⎪=⎨⎪⎩其它.27、设随机变量~(0,1)X U ，求随机变量XY e =的密度函数？ 解：由题意知，当1y ≤时，有()()0Y F y p Y y =≤=当1y e <<时，有()()()(ln )(ln )X Y X F y p Y y p e y p X y F y =≤=≤=≤=当y e ≥时，有()()1Y F y p Y y =≤=即Y 的分布函数1()(ln )11Y X y F y F y y e y e≤⎧⎪=<<⎨⎪≥⎩于是，Y 的密度函数()()Y Y f y F y '=(ln )10XF y y e'<<⎧=⎨⎩其它110y ey ⎧<<⎪=⎨⎪⎩其它.28、随机变量X 的密度函数为0()0xX e x f x x -⎧>=⎨≤⎩求随机变量2Y X =的密度函数？解：由于20Y X =≥，故当0y <时，有()()0Y F y p Y y =≤=； 当0y ≥时，有2()()()(Y F y p Y y p X y p X =≤=≤=≤0()1x X f x dx dx e -===-即Y 的分布函数10()0Y e y F y y ⎧-≥⎪=⎨<⎪⎩ 于是，Y 的密度函数0()()00Y Y y f y F y y >'==≤⎩.29、设随机变量~(0,1)X N ，试求随机变量||Y X =的密度函数？ 解：由于||0Y X =≥，故当0y <时，有()()0Y F y p Y y =≤=； 当0y ≥时，有()()(||)()2()1Y F y p Y y p X y p y X y y =≤=≤=-≤≤=Φ-即Y 的分布函数2()1()00Y y y F y y Φ-≥⎧=⎨<⎩于是，Y 的密度函数()()Y Y f y F y '=2()y y y 'Φ>⎧=⎨≤⎩22000yy y ->=≤⎩.B 组1、A2、B3、D4、B5、B6、B7、C8、C9、C10、C11、设随机变量X 的分布函数为0111()21232x a x F x a x a bx <-⎧⎪-≤<⎪⎪=⎨-≤<⎪⎪+≥⎪⎩且1(2)2p X ==，求常数a 、b ？ 解：由()1F +∞=及()()(0)p X a F a F a ==--得()121(2)(2)(20)()()32F a b p X F F a b a +∞=+=⎧⎪⎨==--=+--=⎪⎩1726a b a b +=⎧⎪⇒⎨+=⎪⎩1656a b ⎧=⎪⎪⇒⎨⎪=⎪⎩.12求常数a ？解：由11ii p+∞==∑得20.5121a a +-+=12a ⇒=±再由11202a a -≥⇒≤，可得12a =-. 13、口袋中有5个球，编号为1、2、3、4、5，从中任取3个，以X 表示取出的3个球中的最大号码.(1) 求X 的分布列； (2) 求X 的分布函数？解：(1) 由题意知X 是离散型随机变量，其所有可能取值为3、4、5，且22351(3)10C p X C ===、23353(4)10C p X C ===、24356(5)10C p X C ===于是X(2) 由(1)可知的分布函数为030.134()0.44515x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩.14、设随机变量X 的密度函数为||()x af x Ce-= (0)a >求(1) 常数C ；(2) X 的分布函数；(3) (||2)p X <？解：(1) 由()1f x dx +∞-∞=⎰得||()2221x x aaf x dx C e dx C e dx aC +∞+∞+∞---∞====⎰⎰⎰12C a⇒=； (2) 当0x <时 ||111()()222t t xa a a x x x F x f t dt e dt e dt e a a --∞-∞-∞====⎰⎰⎰当0x ≥时||||0011()()22t t a a xx F x f t dt e dt e dt a a---∞-∞==+⎰⎰⎰ 001111222t t x a a a x e dt e dt e a a ---∞=+=-⎰⎰于是102()1102xa x a e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩；(3) 22211(||2)(22)(2)(2)1122a a a p X p X F F e e e ---<=-<<=--=--=-. 15、设随机变量X 的密度函数为201()0xx f x ≤≤⎧=⎨⎩其它以Y 表示对X 的三次独立重复观察中事件1{}2X ≤出现的次数，求(2)P Y =？解：由题意知：事件1{}2X ≤在一次观察中出现的概率为1112222001()02|4p f x dx dt xdx x -∞-∞==+==⎰⎰⎰ 且~(3,)Y b p ，于是223139(2)()()4464P Y C ===.16、设顾客在某银行的窗口等待服务的时间X (单位：分钟)服从指数分布，其密度函数为510()5x e x f x x -⎧>⎪=⎨⎪≤⎩某顾客在窗口等待服务，若超过10分钟他就离开.他一个月要到银行5次，以Y 表示一个月内他未等到服务而离开窗口的次数，求(1)p Y ≥？解：由题意知：顾客在窗口等待服务的时间超过10分钟的概率为5521010101()|5x x p f x dx e dx e e +∞+∞--+∞-===-=⎰⎰且~(5,)Y b p ，于是2025255(1)1(0)1()(1)1(1)0.5167P Y P Y C e e e ---≥=-==--=--=. 17、设随机变量2~(2,)X N σ且(24)0.3p X <<=，求(0)p X <？解：由2~(2,)X N σ得224242(24)()()(0)0.3p X p X σσσ---<<=<<=Φ-Φ=2()0.8σ⇒Φ=0222(0)()()1()10.80.2p X p X σσσ-⇒<=<=Φ-=-Φ=-=.18、设随机变量X 的分布函数为()F x ，试求随机变量()Y F X =的密度函数？ 解：由于0()1F X ≤≤，故当0Y <时，有()()0Y F y p Y y =≤=； 当01y ≤≤时，有11()()(())(())(())Y F y p Y y p F X y p X F y F F y y --=≤=≤=≤==当1y >时，有()()1Y F y p Y y =≤= 即Y 的分布函数00()0111Y y F y yy y <⎧⎪=≤≤⎨⎪>⎩于是，Y 的密度函数()()Y Y f y F y '=101y <<⎧=⎨⎩其它即随机变量Y 服从区间(0,1)上的均匀分布.初夏早上六点，清亮透明的月儿还躲藏在云朵里，不忍离去，校园内行人稀少，我骑着单车，晃晃悠悠的耷拉着星松的睡眼。

第二章 习题解答2.5试求半径为a ，带电量为Q 的均匀带电球体的电场。

解：以带电球体的球心为球心，以r 为半径，作一高斯面，由高斯定理S D dS ∙⎰ =Q ，及D E ε= 得，错误！未找到引用源。

r ≤a 时， 由S D dS ∙⎰ =224433Qr a ππ⨯，得34Qr D a π= 304Qr E a πε= 错误！未找到引用源。

r>a 时，由S D dS ∙⎰ =Q ，得34Qr D r π= 304Qr E rπε= 2.5 两无限长的同轴圆柱体，半径分别为a 和b （a<b ），内外导体间为空气。

设同轴圆柱导体内、外导体上的电荷均匀分布，其电荷密度分别为1S ρ和2S ρ，求： 错误！未找到引用源。

空间各处的电场强度；错误！未找到引用源。

两导体间的电压；错误！未找到引用源。

要使ρ>b 区域内的电场强度等于零，则1S ρ和2S ρ应满足什么关系？解：错误！未找到引用源。

以圆柱的轴为轴做一个半径为r 的圆柱高斯面，由高斯定理S D dS ∙⎰ =q及D E ε= 得，当0<r<a 时，由S D dS ∙⎰ =q=0，得D =0，E =0当a ≤r ≤b 时，由S D dS ∙⎰ =q,得D r l π⨯2⨯= 1S ρa l π⨯2⨯D =1S r e r ρ ，10S r aE e rρε= 当b<r 时，由S D dS ∙⎰ =q,得D r l π⨯2⨯= 1S ρa l π⨯2⨯+2S ρb l π⨯2⨯D =12s s r a b e r ρρ+ ，E =120s s r a b e rρρε+ Equation.DSMT4 11ab 00ln b b s s a a a a a E dr dr r b ρρεε∅===⎰⎰ Equation.DSMT4 ρ>0的区域外电场强度为0，即：E =120s s r a b e rρρε+ =0，得1S ρ=2s b a ρ- 2.9 一个半径为a 的薄导体球壳，在其内表面覆盖了一层薄的绝缘膜，球内充满总电量为Q的电荷，球壳上又另充了电量为Q 的电荷，已知内部的电场为4()r r E a a= ，计算： = 2 \* GB2 ⑵球的外表面的电荷分布；布；= 4 \* GB2 ⑷球心的电位。

微机原理第二章习题与分析解答1．单项选择题（1）8086工作最大方式时应将引脚MN/MX接（）A．负电源 B.正电源 C.地 D.浮空分析：8086规定工作在最小方式下MN/MX接+5V，工作在最大方式下MN/MX 接地。

答案：C（2）8086能寻址内存储器的最大地址范围为（）A．64KB分析：8086有A0~A1920条地址总线，220=1MB。

答案：B|（3）在总线周期，8086CPU与外设需交换（）A．地址信息 B.数据信息 C.控制信息、B、C分析在总线周期，CPU必须发出地址信息的控制信息以后，才能实现与外设进行交换数据。

答案：D（4）8086用哪种引脚信号来确定是访问内存还是访问外设（）A．RD IO分析：引脚信号M/IO是Memory or Input Output的缩写，当M/IO=0时，用以访问外设；当M/IO=1，用以访问外设。

答案：C（5）在8086指令系统中，下列哪种寻址方式不能表示存储器操作数（）A．基址变址寻址B.寄存器寻址C.直接寻址 D.寄存器间接寻址"分析：8086指令系统共有七种寻址方式，只有立即寻址方式和寄存器寻址方式不是表示存储器操作数的。

答案：B（6）当CPU时钟频率为5MHz，则其总线周期（）A．0．8 s μs分析：时钟周期T=1/ƒ=200ns,而一个总路线周期通常由4个T状态组成，有4╳T=4╳200ns=μs.答案：A（7）8086工作在最大方式下，总路线控制器使用芯片（）A．8282 B.8286分析：在最大方式下，系统中主要控制信号是由总路线控制器产生，而只有芯片8288才有这方面的功能。

答案：D…（8）取指令物理地址=（）A．（DS）╳10H+偏移地址 B.（ES）╳10H+偏移地址C．（SS）╳10H+（SP） D.（CS）╳10H+（IP）分析：每当8086CPU取指令时，总是根据CS：IP的所指的存贮单元去取指答案：D（9）一个数据的有效地址是2140H、（DS）=1016H，则该数据所在内存单元的物理地址为（）Ａ.１２３００H分析：存贮器操作数的物理地址计算方法为：（DS）╳10H+有效地址，即1016H ╳10H+2140H=122A0H答案：B（10）在8086中用一个总路线周期访问内存，最多能读/写（）字节。

第2章习题解答1.文法G[S]为：S->Ac|aBA->abB->bc写出L(G[S])的全部元素。

[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}==============================================2. 文法G[N]为：N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么？[答案]G[N]的语言是V+。

V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D===============================================3.已知文法G[S]：S→dAB A→aA|a B→ε|bB问：相应的正规式是什么？G[S]能否改写成为等价的正规文法？[答案]正规式是daa*b*；相应的正规文法为(由自动机化简来)：G[S]:S→dA A→a|aB B→aB|a|b|bC C→bC|b也可为(观察得来):G[S]:S→dA A→a|aA|aB B→bB|ε===================================================================== ==========4.已知文法G[Z]：Z->aZb|ab写出L(G[Z])的全部元素。

[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}===================================================================== =========5.给出语言{a n b n c m|n>=1,m>=0}的上下文无关文法。

第2章习题解答题2-1 用真值表证明下列恒等式。

(1) ()A B C AB AC ⊕=⊕(2) ()()()()()A B A C B C A B A C ''+++=++ (3) ()0A B A B A B '⊕==⊕⊕解：将输入变量所有的取值逐一代入公式两边计算，然后将计算结果列成真值表。

如果两边的真值表相同，则等式成立。

（1）证明()A B C AB AC ⊕=⊕表JT2-1(2) 证明 ()()()()()A B A C B C A B A C ''+++=++表JT2-2(3) 证明()0A B A B A B '⊕==⊕⊕表JT2-3题2-2 证明下列逻辑等式（证明方法不限）。

(1)()()BC D D B C AD B B D '''++++=+(2) A C A B BC A C D A BC ''''''''+++=+(3) ()ABCD A B C D AB BC CD A D '''''''''+=+++ (4) ()()()A C B D B D AB BC '''+++=+解：在实际应用中，除非逻辑式很简单、而且逻辑变量数很少的情况下，一般不宜用列真值表的方法。

对多变量、复杂的逻辑等式、通常采用公式推演或公式推演与画卡诺图相结合的方法去证明。

如果有条件使用Multisim 等EDA 软件进行证明，则更简单、便捷。

(1)()()()()BC D D B C AD B BC D B C AD B BC D AB D AC D BB BC B D'''''++++=++++''''=+++++=+(2)()A C A B BC A C D A C A B BC A BC BC A BC ''''''''''''''+++=++=+=+(3)()()()()()()()()()()()AB BC CD A D AB BC CD A D A B B C C D A D A B A C BC AC AD C D ABCD A B C D '''''''''''''+++=''''''''''=++++=++++''''=+ (4)()()()()()()A C B D B D A C B BD BD A C B AB BC ''''''+++=+++=+=+题2-3已知逻辑函数Y 1和Y 2的真值表如表JT2-4（a ）、（b ）所示，试写出Y 1和Y 2的逻辑函数式。