电工学第2章习题答案

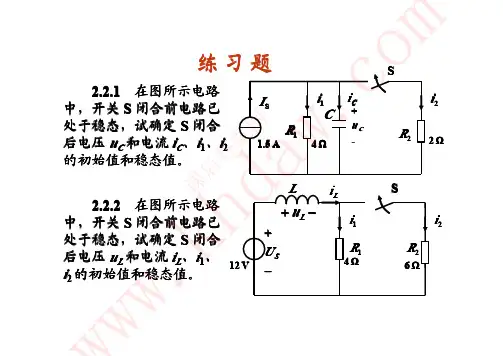
2-1. 列出以下节点的电流方程式，并求出x I 。

解：(a) 由KCL 得：1234()()()0x I I I I I +-+-+-+= ∴2341x I I I I I =++-;(b) 由KCL 得：39(5)()0x I ++-+-= ∴7x I A =(c) 由KCL 之推广得:69()0x I ++-= ∴15x I A =(d) 由KCL 得：1(2)(3)40x I +-++-+= ∴0x I =2-2. 列出以下回路的电压方程式，并标出回路循环方向，求出U 。

解：(a) 回路循环方向与I 方向相同，由KVL 得：U+(2S U -)+I R ⋅=0 ∴U = 2S U -I R ⋅(b) 回路循环方向与3I 、4I 方向相同，由KVL 得：44I R ⋅+33I R ⋅+(U -)=0 ∴U = 44I R ⋅+33I R ⋅(c) 回路循环方向为逆时针方向，由KVL 得：U+(9-)+7=0 ∴U = 2V(d) 设回路电流大小为I ，方向为逆时针方向，由KVL 得：2S U +I ⋅4+I ⋅6+(1S U -)+I ⋅3+I ⋅7=0 ∴I = 0.3A因此，U=2S U +I ⋅4 =2-3. 求出下列电路中的电流I 。

解：(a) 由KCL ，流过2Ω电阻的电流大小为(9+I)，对2Ω电阻与10V 电压源构成的回路，由KVL ，得：(9)I +⋅2+(10-) =0, 因此，I ＝－4A ；(b) (2)I -⋅3+6＝0； ∴I = 4A;(c) 流过3Ω电阻的电流 1I ＝93÷＝3A流过6Ω电阻的电流 2I ＝(6+9) ÷6＝2.5 A(d) 由KCL ，I + 3-3＝0 ∴I =0;2-4. 求出下列电路中的电压U 。

解：(a) (U/10 + U/10) ⨯5 + U = (4-U/10-U/10) ⨯10 ∴U=10V ；(b) 10⨯2 + 10 + U ＝0 ∴U=－30V(c) 1I =10⨯(64)(46)(64)++++=5A; 2I =10⨯(46)(46)(64)++++=5A; 4⨯1I + U + 6⨯(－2I )=0; ∴U = 10V(d) U + 18⨯393+－=0; ∴U = 02-5. 有50个彩色白炽灯接在24V 的交流电源上，每个白炽灯为60W ，求每个白炽灯的电流及总电流，另外消耗的总功率为多少 答：每个白炽灯上消耗的功率为2U P UI R==，而U ＝24V ，P ＝60W ， 因此每个白炽灯的电流为P I U =＝2.5A ，总电流为I 总＝I ⨯ 50＝125A 消耗的总功率为P 总＝P ⨯ 50＝3000W2-6. 在220V 单相交流电源上，接有两台电阻热水器，一台为，一台为3kW ，分别求这两台电热器的电阻。

《电工学》作业答案第二章 2-9解：变换过程如图所示，解得I 4 = 2A 。

2-10解：对结点a 列KCL 方程1230I I I对左、右边的网孔列KVL 方程1122S1S20R I R I U U 2233S2S30R I R I U U将数据代入上述方程，联立求解方程组12312230124243204432120I I I I I I I解得1231A 5A 6A I I I ，， 2-11解：对结点a 和b 列KCL 方程13S1S223S2S300I I I I I I I I对回路abca 列KVL 方程22S 11330R I U R I R I将数据代入上述方程，联立求解方程组132321362023022420I I I I I I I解得1232A 1A 2A I I I ，，2-12 解：根据两个结点电路中结点电压方程的一般形式得S1S2S3123a 12312612346V 6V 111111346U U U R R R U R R R 电流I 3可用欧姆定律求得a S333612A 3A 6U U I R2-14解：(a)电路图； (b)电压源U S 单独作用的电路； (c)电流源I S 单独作用的电路电压源U S1单独作用时，将U S2短路，电路如 (b)所示S1123123321232312318A 3.6A 6336333.6A 1.2A 6363.6A 2.4A63U I R R R R R R I I R R R I I R R电压源U S2单独作用时，将U S1短路，电路如图 (c)所示S2213213312131321315A 2A 3362332A 1A3332A 1A33U I R R R R R R I I R R R I I R RU S 和I S 共同作用时111222333 3.61A 2.6A 1.22A 0.8A 2.41A 3.4A I I I I I I I I I 2-16解：(a)I S1单独作用的电路； (b)I S2单独作用的电路； (c)U S 单独作用的电路电流源I S1单独作用时，电路如 (a)所示2S12333A 1.8A 32R I I R R电流源I S2单独作用时，电路如 (b)所示3S22325A 2A 32R I I R R电压源U S2单独作用时，电路如 (c)所示S 2315A 3A 32U I R RI S1、I S1和U S 共同作用时1.823A 6.8A I I I I2-19 解：(a) 求开路电压的电路； (b)求除源电阻的电路； (c) 戴维南等效电路求开路电压的等效电路如 (a)所示。

一、选择题1、如图所示，其节点数、支路数、回路数及网孔数分别为（C ）。

A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示，I=（B ）A。

A、2B、7C、5D、63、如图所示，E=（B ）V。

A、3B、4C、—4D、—3/4、如图所示电路中，I1和I2的关系为（C ）。

A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示，求I1和I2的大小。

解：对于左边节点：I1=10+3+5=18A对于右边节点：I2=10+2-5=7A6、基尔霍夫第一定律的依据是（D ）A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定￥7、理想电压源和理想电流源间（C ）A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是（D ）A.在电路节点处，各支路电流参考方向可以任意设定。

B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。

C.基尔霍夫电压定律应用于任意闭合路径。

D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中，其内阻与理想电压源和电流源之间的正确连接关系是（C）A.理想电压源与内阻串联，理想电流源与内阻串联"B.理想电压源与内阻并联，理想电流源与内阻串联C.理想电压源与内阻串联，理想电流源与内阻并联D.理想电压源与内阻并联，理想电流源与内阻并联10、79.下面的叙述正确的是（B ）。

A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。

;2、电路中的_____每一分支_______称为支路，____3条或3条以上支路___所汇成的交点称为节点，电路中__________闭合的电路______________都称为回路。

电工学第二章习题一、填空题1． 两个均为40F μ的电容串联后总电容为 80 F μ，它们并联后的总电容为 20 F μ。

2. 表征正弦交流电振荡幅度的量是它的 最大值 ；表征正弦交流电随时间变化快慢程度的量是 角频率ω ；表征正弦交流电起始位置时的量称为它的 初相 。

三者称为正弦量的 三要素 。

3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ；电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ；电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。

由上述三个关系式可得， 电阻 元件为即时元件； 电感 和 电容 元件为动态元件。

4. 在RLC 串联电路中，已知电流为5A ，电阻为30Ω，感抗为40Ω，容抗为80Ω，那么电路的阻抗为 50Ω ，该电路为 容 性电路。

电路中吸收的有功功率为 750W ，吸收的无功功率又为 1000var 。

二、选择题1. 某正弦电压有效值为380V ，频率为50Hz ，计时始数值等于380V ，其瞬时值表达式为（ B ） A 、t u 314sin 380=V ；B 、)45314sin(537︒+=t u V ；C 、)90314sin(380︒+=t u V 。

2. 一个电热器，接在10V 的直流电源上，产生的功率为P 。

把它改接在正弦交流电源上，使其产生的功率为P/2，则正弦交流电源电压的最大值为（ D ） "A 、；B 、5V ；C 、14V ；D 、10V 。

3. 提高供电电路的功率因数，下列说法正确的是（ D ）A 、减少了用电设备中无用的无功功率；B 、减少了用电设备的有功功率，提高了电源设备的容量；C 、可以节省电能；D 、可提高电源设备的利用率并减小输电线路中的功率损耗。

4. 已知)90314sin(101︒+=t i A ，︒+=30628sin(102t i ）A ，则（ C ）A 、i1超前i260°；B 、i1滞后i260°；C 、相位差无法判断。

第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。

试求3I 和4I 。

4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。

R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。

Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。

I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。

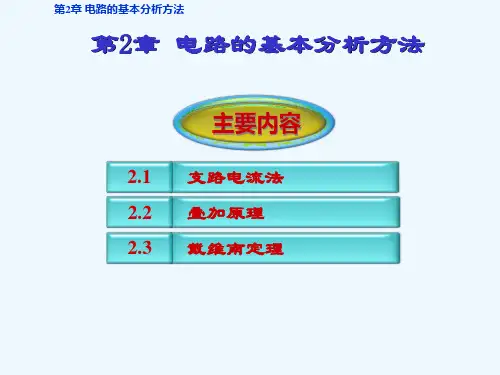
基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

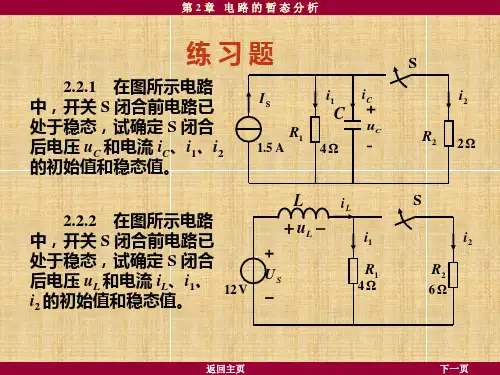
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

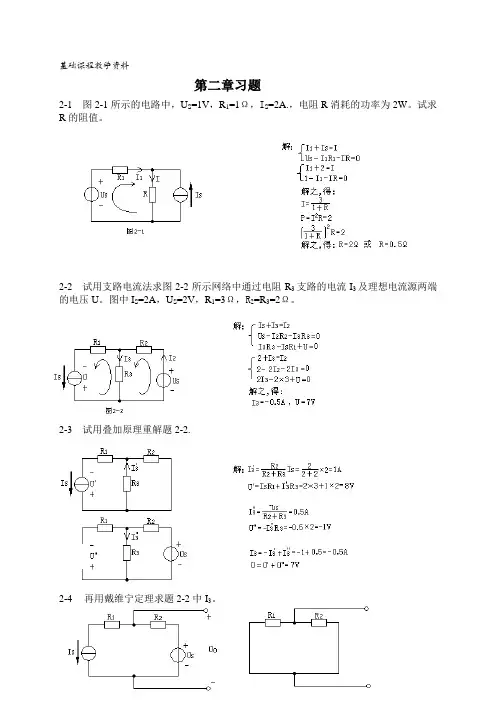
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征，特别是有效值、初相位和相位差。

(2) 掌握正弦量的各种表示方法及相互关系。

(3) 掌握正弦交流电路的电压电流关系及复数形式。

(4) 掌握三种单一参数（R ，L ，C ）的电压、电流及功率关系。

(5) 能够分析计算一般的单相交流电路，熟练运用相量图和复数法。

(6) 深刻认识提高功率因数的重要性。

(7) 了解交流电路的频率特性和谐振电路。

2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值（U m ，E m ，I m ）、瞬时值（u, e, i ）、有效值（U ，E ，I ）。

注：有效值与幅值的关系为：有效值2幅值=。

(2) 频率（f ）、角频率（ω）、周期（T ）。

注：三者的关系是 Tf ππω22==。

(3) 相位（ϕω+t ）、初相角（ϕ）、相位差（21ϕϕ-）。

注：相位差是同频率正弦量的相位之差。

2. 正弦量的表示方法 (1) 函数式表示法：。

)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法：例如u 的波形如图2-1-1(a)所示。

(3) 相量（图）表示法：使相量的长度等于正弦量的幅值（或有效值）； 使相量和横轴正方向的夹角等于正弦量的初相角； 使相量旋转的角速度等于正弦量的角速度。

注：例。

)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解：因为同频率同性质的正弦量相加后仍为正弦量，故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。

解1：相量图法求解如下：具体步骤为三步法（如图2-1-2所示）：第一步：画出正弦量u 1、u 2的相量12U U 、（U 1=6，U 2=4）。

第二步：在相量图上进行相量的加法，得到一个新相量U。

第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。

解: 用电源等值互换法将电流源变换成电压源，将电阻R 2和R 3合并成电阻R 23，其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。

求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流，用分流公式，可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。

已知E 1=230V , R 01=0.5Ω，E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω，试分别用支路电流法和结点电压法求各支路电流 。

解:（1）用支路电流法：各支路电流参考方向已画在图2.16中。

列结点电压方程 L I I I =+21列回路电压方程L L 0222LL 0111R I R I E R I R I E +=+=S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图联立求解上述三各方程式组成的方程组，可得A 40A2021===L I I I验算：按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- （正确！）（2）用结点电压法求解：先求端电压U ，有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。

2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点，则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。

电工第二章试题及答案一、选择题（每题2分，共10分）1. 电流的单位是（）。

A. 安培（A）B. 伏特（V）C. 瓦特（W）D. 欧姆（Ω）2. 电阻的计算公式是（）。

A. R = V/IB. R = V * IC. R = I^2/VD. R = V^2/I3. 并联电路中，总电阻的倒数等于各分电阻倒数之和，这是（）。

A. 欧姆定律B. 基尔霍夫电压定律C. 基尔霍夫电流定律D. 电阻并联原则4. 交流电的有效值是其最大值的（）。

A. 1/√2B. √2C. 2D. 15. 电路中，功率的计算公式是（）。

A. P = V * IB. P = V^2 / RC. P = I^2 * RD. A 和 C 都是二、填空题（每题2分，共10分）1. 电路中，电压是_______和_______之间的电势差。

2. 纯电阻电路中，电流与电压之间的相位关系是_______。

3. 电感的单位是_______，用符号_______表示。

4. 电容器的充放电过程遵循_______定律。

5. 在串联电路中，总电压等于各分电压之_______。

三、简答题（每题10分，共20分）1. 请简述欧姆定律的内容及其应用场景。

2. 什么是三相交流电？它有哪些优势？四、计算题（每题15分，共30分）1. 一个电阻为10Ω的电阻器与一个电容为5μF的电容器串联，已知电源电压为220V（交流），50Hz。

请计算电路的总阻抗，并求出电路中的电流。

2. 一个星形连接的三相交流电路，每相电阻为10Ω，电感为0.5H，电容为100μF。

若电源线电压为380V，50Hz，求电路的总功率。

五、判断题（每题5分，共10分）1. 在纯电容电路中，电流总是超前于电压。

（）2. 功率因数是衡量电路效率的物理量，它等于电路的视在功率与有功功率之比。

（）六、解答题（每题20分，共20分）请解释什么是谐振频率，并说明在RLC串联电路中，谐振频率是如何影响电路的阻抗和电流的。

第二章电路分析基础2-1 电路如图所示，已知US1=24V，US2=16V，IS=1A，R1=R2=8Ω，R3=4Ω。

试用支路电流法求各支路电流。

解：该题有四条支路其中一条支路是恒流源（设恒流源两端电压为U IS），应列四个方程。

有两个节点，按KCL定理可列一个节点方程： I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程：I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。

已知I S=2A，U S=6V，R1=R2=3Ω，R3=R4=6Ω，用叠加原理求a、b两点之间电压U ab。

解：当电压源U S单独作用时，题图变如右图：Uab1=当电流源I S单独作用时，题图变如右图Uab2=3V Uab=Uab1+Uab2=2-3 电路如图所示。

已知R1=6Ω，R2=12Ω，R3=8Ω，R4=4Ω，R5=1电路中流经R3的电流I当电流源I S单独作用时，题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中，当U S=24V时，Uab=8v. 试用叠加原理求U S=0时的UabIs。

解：当电压源U S单独作用时，题图变如右图)(1841243ARRUI S=+=+='解：以知U S=24V时，Uab=8v.当U S、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得：Uab1=)(64244VRRUS-=-=⨯；由图2可得：Uab2=)(212411VRIRRISS=⨯；由图3可得：Uab3=)(41422VRIRISS=⨯；UabIs=Uab2+Uab3=8+6=14（V）2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I。

电工学1第二章作业1. 用戴维宁定理求图示电路中的I ，求5A 电流源的功率P ，并说明它是电源还是负载。

U abK +204+4-456+4⨯⨯=0 U abK =8VR 0=4//6+4=6.4Ω I=8/(6.4+1.6)= 1A (5-1）×4— 4— U+5×5=0U= 37V P=—5×37 = — 185W 电源思考题: 1. 对待求支路来说，其它电路相当于什么？（这是戴维宁定理的核心） 答: 相当于一个实际的电流源 2. 为什么要将待求支路断开？答：令等效电阻上无电流，不分压。

3. 断开后，电路结构发生什么变化？被分成几部分？ 答: 电路被分成左右两部分。

4. 等效电阻求解时，为什么电压源要短路？电流源要断路？ 答：将有源二端网络变为无源二端网络。

5. 电流源两端电压求解时，能否熟练掌握KVL 定律？ 一要会选合适的闭合回路（元件个数少且不含恒流源），二是注意电压参考方向与绕行方向的关系。

2. 用叠加原理求图示电路中的I 。

电压源单独作用，I ′=3//3(9)/333//3⨯+=1A 电流源单独作用，I 〞=239213//333-⨯⨯+++=—2AI=1—2=—1A思考题：1. 叠加原理要令各个电源单独作用，最后做叠加，9A 单独作用时，I 是正的还是负的？ 叠加时是相加还是相减？2. 如果要求电流源的功率，可以用叠加原理吗？ 答：功率不可以用3.叠加原理还能处理哪些特殊的电路？ 答：加减电源，改变电源参数的电路。

20V6Ω5AUI3Ω* 思考题可以帮助大家更好的理解所学内容，在心里思考就行了,不用写出。