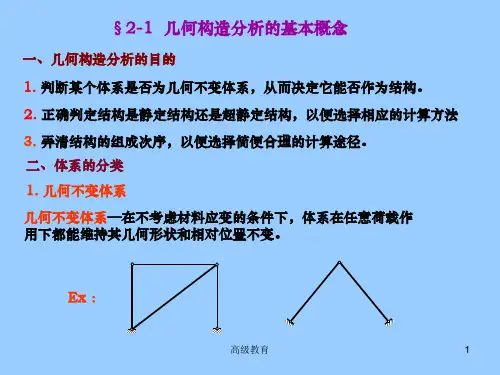
结构的几何构造分析概念1-11、几何组成分析的目的主要是分析、判断一个体系是否几何可变，或者如何保证它成为几何不变体系，只有几何不变体系才可以作为结构。
几何可变体系：不考虑材料应变条件下，体系的位置和形状可以改变的体系。
几何不变体系：不考虑材料应变条件下，体系的位置和形状保持不变的体系。
2、自由度：描述几何体系运动时，所需独立坐标的数目。
平面内一个动点A，其位置要由两个坐标 x 和 y 来确定，所以一个点的自由度等于2。
平面内一个刚片，其位置要由两个坐标 x 、y 和AB 线的倾角α来确定，所以一个刚片在平面内的自由度等于3。
3、刚片：平面体系作几何组成分析时，不考虑材料应变，所以认为构件没有变形。
可以把一根杆、巳知是几何不变的某个部分、地基等看作一个平面刚体，简称刚片。
4、约束：如果体系有了自由度，必须消除，消除的办法是增加约束。
约束有三种：5、多余约束：减少体系独立运动参数的装置称为约束，被约束的物体称为对象。
使体系减少一个独立运动参数的装置称为一个约束。
例如一根链杆相当于一个约束;一个连接两个刚片的单铰相当于二个约束;一个连接n个刚片的复铰相当于n—1个单铰;一个连接二个刚片的单刚性节点相当于三个约束;一个连接n 个刚片的复刚性节点相当于n—1个单刚性节点。
如果在体系中增加一个约束，体系减少一个独立的运动参数，则此约束称为必要约束。
如果在体系中增加一个约束，体系的独立运动参数并不减少，则此约束称为多余约束。
平面内一个无铰的刚性闭合杆(或称单闭合杆)具有三个多余约束。
6、瞬变体系及常变体系：常变体系概念：体系可发生大量的变形，位移。
区别于瞬变体系：瞬变体系概念：体系可发生微小的变形，位移。
7、瞬铰：两刚片间以两链杆相连，其两链杆约束相当(等效)于两链杆交点处一简单铰的约束，这个铰称为瞬铰或虚铰。
2-2平面杆件体系的计算自由度1、体系是由部件（刚片或结点）加上约束组成的。
2、刚片内部：是否有多余约束。
内部有多余约束时应把它变成内部无多余约束的刚片，而它的附加约束则在计算体系的约束总数时应当考虑进去。
3、复铰：连接两个以上刚片的铰结点。
连接n个刚片的铰相当于（n-1）个单铰。
4、单链杆：连接两个铰结点的链杆。
5、连接两个以上铰结点的链杆。
连接 n 个铰结点的复链杆相当于(2n-3)个单链杆。
6、平面体系的计算自由度 W ：W=3m-(2n+r) m:钢片数 n:单绞数 r:支座链杆数上面的公式是通用的。
W=2J-(b+r) J:结点个数 b:链杆数 r:支座链杆数上面的公式用于完全由铰接的连杆组成的结构体系。
7、自由度与几何体系构造特点：静定结构的受力分析一、二、梁的内力主要采取截面法，截面法可以用六个字描述：2、截面内力计算的基本方法：截面法：截开、代替、平衡。
内力的直接算式：直接由截面一边的外力求出内力。
1、轴力=截面一边的所有外力沿轴切向投影代数和。
2、剪力=截面一边的所有外力沿轴法向投影代数和，如外力绕截面形心顺时针转动，投影取正否则取负。
3、弯矩=截面一边的所有外力对截面形心的外力矩之和。
弯矩及外力矩产生相同的受拉边。
静定结构影响线当结构上作用有与杆件主轴正交的、沿结构跨度移动的单位集中荷载（P=1）时，用以表示确定的截面或位置上某一特定的受力效果（内力、位移或支座反力）的变化规律的函数图形（曲线），称为该结构在荷载作用下某一截面特定受力效果的影响线，简称影响线。
概念桥梁上行驶的火车、汽车，活动的人群，吊车梁上行驶的吊车等等，这类作用位置经常变动的荷载称为移动荷载。
常见的移动荷载有：间距保持不变的几个集中力（称为行列荷载）和均布荷载。
为了简化问题，我们往往先从单个移动荷载的分析入手，再根据叠加原理来分析多个荷载以及均布荷载作用的情形。
对于工程计算中的各种物理量和几何量，我们统称为量值，记作Z。
由于移动荷载的作用位置是变化的，使得结构的支座反力、截面内力、应力、变形等等也是变化的。
因此，在移动荷载作用下，我们不仅要了解结构不同部位处量值的变化规律，还要了解结构同一点处的量值随荷载位置变化而变化的规律，以便找出可能发生的最大内力是多少，发生的位置在哪里，此时荷载位置又怎样，从而保证结构的安全设计和施工。
在竖向单位移动荷载作用下，结构内力、反力或变形的量值随竖向单位荷载位置移动而变化的规律图像称为影响线。
计算利用某量值S（某支座反力、某截面弯矩、剪力等）的影响线，求位置一定的一组荷载产生的该量值S之值（叫S的影响量）。
（图1）作用在影响线同一直线线段上的各力的影响等于其合力的影响，即（图2）。
其成立的条件是各力位于S影响线的同一直线线段上。
据此，不能将S影响线顶点B两侧之力以一个合力代替去计算S。
均布荷载产生的影响量S等于荷载集度口与荷载下面的S影响线的面积的乘积，即。
注意；均布荷载下面的影响线纵标有正有负，因此，面积也有正有负，这个结论，对于曲线型影响线（如静不定力影响线）也是成立的。
对于位于影响线同一直线段上的分布荷载也可用其合力代替去求影响量。
影响方程在思路上与静定结构内力影响线一样一是建立影响方程；二是建立影响方程的方法，与固定荷载作用下求内力的方法相同。
即静定结构用平衡方程建立影响方程，而超静定结构则用解超静定的方法——力法、位移法、力矩分配法等建立影响方程。
根据影响方程来绘制影响线的方法叫静力法。
用绘制位移图的方法来得到影响线的方法叫机动法。
机动法有一个很大的优点，就是能很快地画出内力影响线的形状，以判定荷载的最不利分布，而这是计算最大内力值所需要的。
①欲绘制超静定结构支座反力R的影响线，则去掉相应联系（支杆），把支杆反力R暴露出来，沿反力R正向加一个力使与之相应的广义位移（竖向位移）等于1，这样得到的位移图（挠度曲线）即为R的影响线。
符号：轴线上面的纵标取正号。
②欲绘制超静定结构弯矩MK影响线形状，应把截面K切断，再用铰联结起来（把刚结变为铰结，丢掉了阻止相对转动的联系）。
沿弯矩正向（使下面受拉）加一对大小任意的力偶矩M。
画出位移图的形状，轴线上方取为正，这就得到了影响线的形状。
③欲绘制超静定结构剪力影响线形状，应把截面K切断，再用一对平行杆联结起来（去掉了阻止相对错动的联系）。
采用这种方式时，左右两部分只能相对错动，而不能相对转动（和沿轴向相对移动），因之体系变形后，左右两部分变形曲线于联结处的切线相互平行。
沿剪力正向加一对任意大小的剪力Q画出位移图，即得影响线的形状。
上面取正号，下面取负号。
由于超静定结构去掉一个联系后仍为一几何不变体系，其位移图是曲线的，所以超静定结构内力的影响线是曲线的。
由于静定结构去掉一个联系后即成为机构（可变体系），其位移图是直线图形，因而静定结构内力影响线是直线图形。
超静定结构中的静定内力（如挑臂上的弯矩、剪力），其影响线也是直线图形。
影响形状均布活荷载的最不利分布①对于跨中载面，当活荷载作用于载面所在跨及每间隔一跨的各跨上时，出现最大正弯矩。
②对于支座截面，当活荷载作用于该支座左右两跨及每间隔一跨的各跨上时，出现最大负弯矩。
③在整个结构上都布满活荷载时，对于支座弯矩、跨中弯矩都不是最不利情况。
④一种内力出现最大（最小）值时，其他内力并不同时出现最大（最小）值。
与活荷载不同，恒荷载经常作用，永远要计算，没有最不利分布问题。
确定行列荷载在什么样的位置上量值s取得最大值，这个行列荷载位置为最不利荷载位置。
得到极大值时行列荷载所处位置的特点是；（1）有一个集中力居于影响线顶点上。
（2）将行列荷载自此左移一点，（图3）是正的，右移一点（图4）是负的。
满足这种条件（使取得极大值）的位于影响线顶点上的集中力叫临界荷载（以表示），与此对应的行列荷载位置，称为临界位置。
（3）MK在行列荷载移动全过程中得到的极大值可能不止一个。
对于三角形影响线：多边形影响线，在由多个集中力组成的行列荷载作用下，都是适用的。
S生极大值所对应的行列荷载位置，必须具备以下两个条件：①有一个集中力位于影响线的顶点上。
②自此位置向左移：自此位置向右移：。
这两个公式称为临界条件，满足临界条件的集中力为临界荷载，相应的荷载位置为临界位置。
把临界荷载算在影响线顶点的哪一边，哪一边单位长度上的平均荷载就大。
对于三角形影响线，求量值S最大值的步骤为：①按前述方法估计能产生最大值的若干可能的临界荷载。
②逐个地把估出的力放在影响线顶点上，验算是否满足临界条件。
如果满足临界条件，则利用影响线求出相应的S，它是S一个极大值。
比较这样求得的几个S极大值，其中最大的就是行列荷载移劫过程中可能产生的最大S 值。
根据临界条件的推导过程知：临界条件中的前一个不等式代表力在左方时后一个不等式代表力在右方时。
若满足前一个不等式，而不满足后一个不等式，就表明不论把力放在左面，还是放在右面，都有即越往右移S越大。
因此应把行列荷载向右移。
反之，若不满足前一个不等式，而满足后一个不等式，则不论力在左、力在右都有即越往右移S越小，因此求S极大值耍向左移动行列荷载。
对于桥梁要考虑车辆右行，左行两种情况，按最不利情况设计。
工业厂房吊车荷载则不会改变方向。
静定结构位移计算一、位移计算引起位移的主要原因：各种因素对静定结构的影响：内力变形位移荷载√√√×√√温度改变或材料胀缩××√支座移动或制造误差引起位移的主要原因有上述三种：①荷载作用、②温度变化、③支座移动和制造误差。
计算方法本章只讨论线性变形体系的位移计算，计算方法是单位荷载法，其理论基础是虚功原理。
线性变形体系和叠加原理的使用条件是：①材料处于弹性阶段，应力与应变成正比；②小变形。
因此可以应用叠加原理计算结构的位移。
虚功和虚功原理（1）实功：力在本身引起的位移上作功，恒为正值（2）虚功：力在其它原因引起的位移上所作的功（力在虚位移上作的功），可正可负如图（9-1）力与位移同向，虚功为正，力与位移反向，虚功为负。
虚位移：与作功的力无关。
是结构的支承条件和变形条件允许的微小位移。
引起位移的原因：可以是一组力，温度变化、支座位移等，也可以是假想的位移，故称为“虚”。
（3）广义力和广义位移：在功的计算公式W=PΔ中，涉及到两方面因素：①与力有关的因素：例如，一个力、一个力偶、一对力、一对力偶。
把这些与力有关的因素称为广义力；②与广义力相应的位移因素：例如，与集中力相应的广义位移是该力的作用点的总全位移在力的方向上的分量；与集中力偶相应的广义位移是它所作用截面的转角；与作用点不同但等值、反向、共线的一对力相应的广义位移是两力作用点沿两力方向的相对线位移；与等值、反向一对力偶相应的广义位移是两力偶作用截面的相对转角，等……。
把这些与位移有关的因素称为广义位移。
广义力与相应广义位移的关系是：它们的乘积是虚功。
