3、动量矩定理及其守恒定律

动量矩守恒定律动量守恒定律动能动量矩守恒定律是物理学中的基本定律之一，它描述了动量和角动量在一个封闭系统内的守恒规律。

动量和角动量是物体运动的两个重要物理量，它们的守恒定律不仅在经典物理学中得到了广泛的应用，也在现代物理学中扮演着重要的角色。

本文将从动量守恒定律和角动量守恒定律的基本概念、应用范围以及实际意义等方面进行深入探讨。

首先，我们来看一下动量守恒定律的基本概念。

动量守恒定律指的是在一个封闭系统内，如果没有外力做功，系统的总动量将保持不变。

换句话说，如果一个物体受到的外力为零，那么它的动量将保持不变。

这个定律可以用数学表达式来描述：Σpi = Σpf，即系统在开始时的总动量等于系统在结束时的总动量。

这个定律适用于各种物体的碰撞、运动、以及其他形式的相互作用，是物理学中最基本的定律之一。

接下来，我们来看一下动量守恒定律的应用范围。

动量守恒定律广泛适用于物体之间的碰撞过程。

在弹性碰撞中，碰撞前后物体的总动量保持不变；在非弹性碰撞中，虽然动能不守恒，但总动量仍然保持不变。

此外，动量守恒定律还适用于各种其他运动过程，例如物体在外力作用下的运动、多体系统的运动等。

在这些情况下，动量守恒定律都可以用来描述系统的运动规律，为我们理解物体之间的相互作用提供了重要的理论支持。

除了动量守恒定律，角动量守恒定律也是物理学中的重要定律之一。

角动量是描述物体旋转运动的物理量，它也满足守恒定律。

具体来讲，如果一个物体受到的外力矩为零，那么它的角动量将保持不变。

这个定律可以用数学表达式来描述：ΣL = ΣLf，即系统在开始时的总角动量等于系统在结束时的总角动量。

角动量守恒定律不仅适用于物体的旋转运动，也适用于机械系统、自旋系统等各种情况。

动量守恒定律和角动量守恒定律的重要性不仅在于它们提供了一种全新的视角来理解物体之间的相互作用，而且在许多实际问题中都具有重要的应用价值。

比如在工程领域中，动量守恒定律可以用来设计各种机械系统，预测物体的运动轨迹，优化能量传递过程等。

三大守恒原理的确立经典力学最常用的是对质点进行矢量分析和建立运动微分方程的方法。

这两种办法在解决单质点，以及有限约束的问题时，得心应手。

但是，当面对的是多质点、多约束的情况时，直接运用这两种方法也就显得太过困难了。

为了解决这个问题，十七、十八世纪的科学家们逐渐发展了动量定理、动量矩定理和活力定理——三大运动定理以及它们在封闭系统环境下的三个积分形式的守恒定律。

经典力学最常用的是对质点进行矢量分析和建立运动微分方程的方法。

这两种办法在解决单质点，以及有限约束的问题时，得心应手。

但是，当面对的是多质点、多约束的情况时，直接运用这两种方法也就显得太过困难了。

为了解决这个问题，十七、十八世纪的科学家们逐渐发展了动量定理、动量矩定理和活力定理——三大运动定理以及它们在封闭系统环境下的三个积分形式的守恒定律。

质心运动守恒定律最早提出运动量守恒定律基本思想的是笛卡儿。

后来荷兰的惠更斯从碰撞问题的研究中也得出了碰撞前后，系统的共同质心运动速度为常数的结论。

最终系统得出这一定律的是牛顿，他在《原理》一书运动的基本定律之后的推论中明确提出了“质心运动守恒定律”，他写道：“两个或两个以上的物体的共同重心，不会因物体本身之间的作用而改变其运动或静止的状态；因此，所有相互作用着的物体如无外来作用和阻碍，其共同重心将或者静止，或者在等速沿一直线运动。

”如果有外力作用，质心的运动就好象一个质点一样，它的质量等于系统中所有物体的总质量，它所受的力即系统所受的所有外力的矢量和，这就是质心运动定理。

而所谓的质心运动守恒定律事实上是这个定理的特殊情况。

动量矩守恒定律由开普勒的第二定律（面积定律），实际上已经具有了动量矩守恒定律的意义。

牛顿在《原理》中把它推广到有心力运动的一切场合，指出一个质点在指向一固定点的力作用下，其半径（由中心点出发）在相等的时间内扫过的面积相等。

这个原理的普遍表述形式为：一个系统只在内力作用下运动时，各点对某中心的动量矩之和才为常数。

在现行的普通物理教材中，力学中的三大守恒定律，即动量守恒定律、动量矩守恒定律和机械能守恒定律。

现代物理学业已证明这些守恒定律是和时空对称性相联系的：动量守恒定律与空间平移对称性相联系；动量矩守恒定律与空间转动对称性相联系；能量守恒定律与时间平移对称性相联系。

由上述对称性可导出相应的守恒定律,进一步导出牛顿运动定律。

动量矩守恒定律，又称角动量守恒定律。

指的是根据动量矩定理推论，当合外力矩为0时，其动量矩保持不变。

表述动量矩守恒条件的定律。

质点不受力或作用力对某固定点(或轴)之矩始终等于零时，该质点对该点(或轴)的动量矩保持不变。

质点系所受外力对某固定点(或轴)之矩的和始终等于零时，该质点系对该点(或轴)的动量矩保持不变。

例如行星所受太阳引力始终指向太阳中心，故如不计其他星体的引力，行星对太阳中心的动量矩守恒
一个系统不受外力或所受外力之和为零，这个系统的总动量保持不变，这个结论叫做动量守恒定律。

1.动量守恒定律是自然界中最重要最普遍的守恒定律之一，是一个实验规律，也可用牛顿第三定律结合动量定理推导出来。

2.相互间有作用力的物体系称为系统，系统内的物体可以是两个、三个或者更多，解决实际问题时要根据需要和求解问题的方便程度，合理地选择系统。

动量矩定理及动量矩守恒定律在篮球投篮技术
动作中的应用
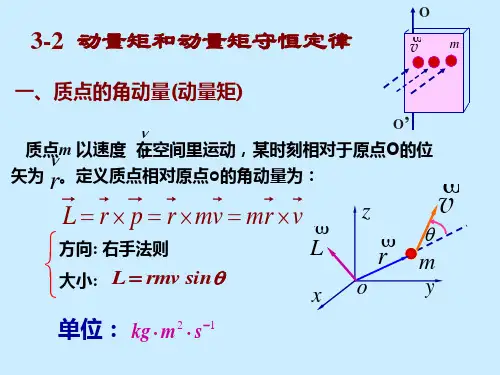
首先，在定义动量矩定理和动量矩守恒定律之前，我们必须要谈论动量矩。

动量矩是一个概念，指的是一个运动物体的运动情况下它的动量和位置之间的关系。

动量矩定理指的是一个物体的总动量矩是常数，即：物体的总动量矩在单位时间内是不变的；
动量矩守恒定律是基于动量矩定理而得出的：物体的总动量是不变的，即物体的总动量在单位时间内是不变的。

从物理学的角度，动量矩定理和动量矩守恒定律都可以应用于篮球投篮技术动作。

比如，我们常用手去投篮。

当我们把手从一定的位置开始投篮时，由于重力，我们的手上有向下的力，也就是我们手上有一定的动量矩。

另外，当我们把手投向篮筐时，我们的另一只手也将施加一个力，以防止发射的力量过大导致篮球飞出较远。

这样，我们的手就具有一定的动量矩，即“动量矩守恒定律”。

此外，当把篮球发射后，由于地心引力，篮球在运动过程中，会向篮筐的底部施加一定的力，这时也可以应用到动量矩定理中去。

篮球的总动量矩会保持不变，所以，篮球的运动轨迹也就能够得到一定的准确性。

总之，动量矩定理和动量矩守恒定律在篮球投篮技术动作中都可以很有效的应用到。

运用这两条定律，可以把篮球的运动轨迹控制的更加准确，从而使篮球能够准确地投入篮筐。

三、动量矩守恒定律上一次课我们从牛顿第二定律出发导出了两条重要推论，一条是动量定理及其守恒定律，另一条就是动量矩定理及其守恒定律。

根据动量矩守恒定律我们还可以证明这样一个特征：力矩为零的质点只能作平面运动。

我们课本上的P.59页的例1，其实就是证明这个结论的例子。

这个例题让我们证明：当质点所受的力，如果恒通过某一个定点，则质点必定在一平面上运动。

下面我们就利用动量矩守恒定律来对它加以证明。

证明：质点所受的力，如果恒通过某一个定点，那么这个定点就叫力心。

例如地球绕太阳运行而受到太阳的引力作用，这些引力的作用线总是通过太阳中心的，这种有力心的力就叫做有心力。

如果我们取力心为坐标原点，那么由于运动质点的位置矢径r与质点所受的力F 是在同一直线上的。

显然，质点所受的力F 对坐标系的原点即力心的力矩 F r ⨯ 是等于零的，即：0=⨯F r 。

所以，此情况下的质点在运动过程中角动量是守恒的。

即c v m r =⨯。

将它写成直角坐标的分量形式的话，则有：m (y ..y z z -)=x c ------(1)m (z ..z x x -)=y c ------(2)m (x ..x y y -)=z c --------（3）我们将（1）z y x ⨯+⨯+⨯)3()2( 即：xm (y ..y z z -)=x c xym (z ..z x x -)=y y c+ zm (x ..x y y -)=z c z0=++z c y c x c z y x 所得到的这个方程，是什么方程？根据空间解析几何知识可知它是一个平面方程。

这就证明了质点只能在这个平面方程所决定的平面上运动。

因此，通过对这个例子的证明，其实也同时包含证明了：力矩为零的质点只能作平面运动的这一特征。

前面，我们根据牛顿第二定律已经得到了两个推论，接下去就讲他的第三个推论。

§6．动能定理与机械能守恒定律在此先介绍有关功与能的几个基本概念和基本物理量。

动量矩守恒定律动量守恒定律动能动量矩守恒定律是物理学中的重要定律之一，它告诉我们在一个封闭系统中，如果外部力矩为零，则系统的角动量将守恒不变。

而动量守恒定律则告诉我们在一个封闭系统中，如果外部力为零，则系统的动量将守恒不变。

这两个定律在物理学中有着广泛的应用，可以帮助我们理解许多物理现象。

首先，让我们来看一下动量守恒定律。

动量是物体的运动状态的量度，它是质量和速度的乘积。

当一个物体受到外部力的作用时，它的动量会发生改变。

然而，如果一个系统是封闭的，即没有外部力的作用，那么系统的总动量将守恒不变。

这就意味着，系统中任何一个物体的动量的改变都会以相等的方式被其他物体所吸收，从而确保系统总动量守恒。

举一个简单的例子来说明动量守恒定律：假设有两个物体A和B 在一条直线上以相同的速度相向而行，它们的质量分别为m1和m2。

当它们发生碰撞时，根据动量守恒定律，它们的总动量在碰撞前后都将保持不变。

假设碰撞后物体A的速度为v1’，物体B的速度为v2’，那么根据动量守恒定律有m1v1 + m2v2 = m1v1’ + m2v2’。

这个简单的例子清楚地展示了动量守恒定律的应用。

接下来，让我们来看一下动量矩守恒定律。

角动量是物体围绕某一轴旋转时的运动状态的量度，它是质量、速度和与轴的距离的乘积。

当一个物体受到外部力矩的作用时，它的角动量会发生改变。

然而，如果一个系统是封闭的，即外部力矩为零，那么系统的总角动量将守恒不变。

举一个简单的例子来说明角动量守恒定律：假设有一个转动的物体在没有外力矩的情况下保持着一定的角速度，当它改变形状或者重新分布质量分布时，它的角动量将保持不变。

这个例子清楚地展示了角动量守恒定律的应用。

总的来说，动量守恒定律和角动量守恒定律是非常重要的物理定律，它们可以帮助我们理解并解释许多物理现象。

在实际应用中，我们可以利用这些定律来计算碰撞、旋转等各种物理过程中的动量和角动量的变化，从而更好地理解系统的运动状态。

动量矩守恒定律及广义动量守恒定律动量是物体运动的重要物理量之一，它描述了物体运动的特征和变化。

动量矩守恒定律和广义动量守恒定律是基本的物理定律，它们在研究运动过程中起着重要的作用。

动量矩守恒定律是指在没有外力作用下，物体的总动量矩守恒。

这个定律可以用数学公式表示为：m1v1 + m2v2 = m1v1' + m2v2'，其中m1和m2分别代表两个物体的质量，v1和v2代表它们的初始速度，v1'和v2'代表它们的最终速度。

这个定律的实质是说，当两个物体发生碰撞时，它们的总动量矩守恒，即初始动量等于最终动量。

这个定律适用于各种碰撞情况，无论是弹性碰撞还是非弹性碰撞。

广义动量守恒定律是指在有外力作用下，物体的总动量守恒。

这个定律可以用数学公式表示为：m1v1 + m2v2 + Fext = m1v1' + m2v2'，其中Fext代表外力的合力。

这个定律的实质是说，当外力作用于物体时，物体的总动量发生变化，但总动量的变化量等于外力对物体的冲量。

这个定律适用于各种力的作用情况，无论是重力、摩擦力还是其他力。

动量矩守恒定律和广义动量守恒定律是相互补充的，它们共同描述了物体运动中动量的变化规律。

动量矩守恒定律适用于没有外力作用的情况，而广义动量守恒定律则适用于有外力作用的情况。

在实际应用中，我们常常将这两个定律结合起来使用，以分析和解决各种物体运动的问题。

动量守恒定律的应用非常广泛。

在物理学中，它被用来解释和预测物体的运动轨迹和速度变化。

在工程领域，它被用来设计和优化各种机械装置和运动控制系统。

在交通运输中，它被用来研究和改进车辆的碰撞安全性。

在体育竞技中，它被用来评估运动员的技术水平和比赛成绩。

总之，动量矩守恒定律和广义动量守恒定律是物理学中重要的基本定律，它们揭示了物体运动中动量的变化规律。

这两个定律的应用范围广泛，对于解决各种物体运动问题具有重要意义。

在实际应用中，我们可以根据具体情况选择合适的定律来分析和解决问题，以推动科学技术的发展和进步。