绵阳市人教版 九年级数学 竞赛专题：代数最值问题(含答案)

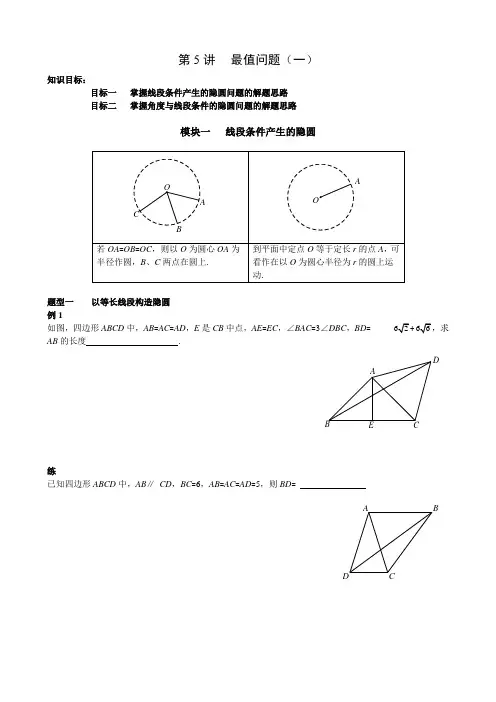
第5讲 最值问题（一）知识目标：目标一 掌握线段条件产生的隐圆问题的解题思路 目标二 掌握角度与线段条件的隐圆问题的解题思路模块一 线段条件产生的隐圆题型一 以等长线段构造隐圆 例1如图，四边形ABCD 中，AB =AC =AD ，E 是CB 中点，AE =EC ，∠BAC =3∠DBC ，BD = AB 的长度 .E DB A练已知四边形ABCD 中，AB ∥ CD ，BC =6，AB =AC =AD =5，则BD =D CBA题型二以定长线段构造隐圆例2在坐标系中，点A坐标为（4，0），点B为y轴正半轴上一点，点C是坐标系中一点，且AC=2，则∠BOC 度数取值范围.练在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°<θ<180°），得到△MNC，P，Q分别是AC、MN的中点，AC=2t，连接PQ，则旋转时PQ长度的最大值是A.B.C. D. 3tQPNMBCA模块二角度与线段条件中的隐图题型一定边对定角例31.在平面直角坐标系中，直线y=-x+6分别与x轴、y轴交于点A、B两点，点P在y轴左边，且∠APB=90，则点P的横坐标a的取值范围是.2.如图，E 、F 是正方形ABCD 的边AD 上两个动点，满足AE =DF ，连接CF 交BD 于点G ，连接BE 交AG 于点H ，若正方形的边长为2，则线段DH 长度的最小值是 .H GF EDCB A3.如图，线段AB 上有一动点M ，分别是以AM 、BM 为边作正方形AMFE 、MBCD ，正方形AMFE 、MBCD 的外接圆⊙O 、 ⊙O ′交于M ，N 两点，则直线MN 的情况是（ ）A .定直线B .经过定点C .一定不过定点D .以上都有可能例41.如图，⊙O 的半径为2，弦AB 的长为P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是.2.如图，△ABC 中，BC =4，∠BAC =45°，以B 、C 两点作⊙O ，连OA ，则线段OA 的最大值为 .练1.如图，P 为正方形ABCD 的边CD 上任意一点，E 为AP 上一点，BE =AB ，∠CBE 的平分线交AP 延长线于点Q ，若正方形的边长为a ，当点P 在CD 边上由C 移动到D 时，则点Q 到CD 的最大距离为 .QP ED CB A2.如图，已知在等边△ABC 中，AB =AC =BC =8，点D 、E 分别是边AC 、AB 上两点，且AE =CD ，BD 交CE 于F ，连接AF ，则AF 的最小值为 .FEDCBA例51.如图，在弓形BAC 中，∠BAC =60°，BC=A 在优弧BAC 上由点B 向点C 移动，记△ABC 的内心为I ，则△ABC 内切圆半径的最大值为.2.如图在扇形AOB中，OA⊥OB，D是AB上一动点，DE⊥OA于E，若OA=△DEO的内心为I，则△DEO内切圆半径的最大值为.B3.如图，已知△ABC，外心为O，BC=10，∠BAC=60°，分别以AB，AC为腰向形外作等腰直角三角形△ABD与△ACE，连接BE，CD交于点P，则OP的最小值是.题型二定边对动角例61.已知A（2，0），B（4，0）是x轴上的两点，点C是y轴上的动点，当∠ACB最大时，则点C的坐标为.2.如图，在展览大厅中，墙壁上的展品最高处点P距离地面2.5米，最低处点Q距地面2米，观赏者的眼睛（在E点）距离地面1.6米，当视角∠PEQ最大时，站在这个位置的观赏效果最理想，求此时E到墙壁的距离为米.3.如图，P 为的⊙O 内的一个定点，A 为⊙O 上的一个动点，射线AP 、AO 分别与⊙O 交于B 、C 两点，若⊙O 的半径长为3，OP，则弦BC 的最大值为（ ）A .B .3 CD .POCBA第5讲 【课后作业】 最值问题（一）1.如图，已知矩形ABCG （AB <BC ）和矩形CDEF 全等，点B 、C 、D 在同一直线上，∠APE 的顶点在折线段B -D -E 上移动，使∠APE 为直角的点P 的个数是 .G F EDCBA2.如图，∠XOY =45°，一把直角三角尺ABC 的两个顶点A 、B 分别在OX 、OY 上移动，其中AB =10，那么点O 到AB 的距离的最大值为 .YO X CB A3.如图，正方形ABCD 的边长为4，∠AED =45°，P 为AB 的中点，当点E 运动时，求PE 的最值.PED CBA4.如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE与点F，当点E从点B出发顺时针运动到点D时，点F所经过的路径长为.5.如图，△ABC中，∠BAC=60°，∠ACB=45°，AC=D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC、于E、F，连接EF，则线段EF的最小值为.。

九年级数学竞赛题：代数最值数学问题中常见的一类问题是：求某个变量的最大值或最小值．在生产实践中，我们经常面对带有“最”字的问题，如投入最少、利益最高、时间最短、效益最大、耗材最少等．我们把这类问题称为“最值问题”．最值问题也是数学竞赛中的热点问题，它内容丰富，涉及面广，解法灵活，解最值问题的常见方法有：1．利用配方法求最值；2．运用不等式或不等分析法求最值；3．建立二次方程，在方程有解的条件下，利用判别式求最值；4．构造二次函数模型求最值；5．构造图形求最值．例1 某乒乓球训练馆准备购买n 副某种品牌的乒乓球拍，每副球拍配k （k ≥3）个乒乓球．已知A 、B 两家超市都有这个品牌的乒乓球拍和乒乓球出售，且每副球拍的标价都为20元，每个乒乓球的标价都为1元．现两家超市正在促销，A 超市所有商品均打九折（接原价的90％付费）销售，而B 超市买1副乒乓球拍送3个乒乓球．若仅考虑购买球拍和乒乓球的费用，请解答下列问题：（1）如果只在某一家超市购买所需球拍和乒乓球，那么去A 超市还是B 超市买更合算？（2）当k =12时，请设计最省钱的购买方案．例2 光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台，现将这50台联合收割机派往A 、B 两地区收割小麦，其中30台派往A 地区，20台派往B 地区．两地区与该农机租赁公司商定的每天的租赁价格见下表：（1）设派往A 地区x 台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y 元，求y 与x 间的函数关系式，并写出x 的取值范围；（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来； 、（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提出一条合理建议．例3已知实数a 、b 、c 满足.4,2==++abc c b a（1） 求a 、b 、c 中最大者的最小值；（2） 求||||||c b a ++的最小值．例4 某商场将进价为30元的书包以40元售出，平均每月售出600个．调查表明：这种书包的售价每上涨1元，其销售量就将减少10个． ’（1）为了实现平均每月10000元的销售利润，这种书包的售价应定为多少元？（2）10000元的利润是否为最大利润？如果是，请说明理由；如果不是，请求出最大利润，并指出此时书包的售价应定为多少元？（3）请分析并回答售价在什么范围内商家就可获得利润．例5如图1，已知直线x y 21-=与抛物线6412+-=x y 交于A 、B 两点． （1）求A 、B 两点的坐标；（2）求线段AB 的垂直平分线的解析式；（3）如图2，取与线段AB 等长的一根橡皮筋，端点分别固定在A 、B 两处．用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动，动点P 将与A 、B 构成无数个三角形，这些三角形中是否存在一个面积最大的三角形？如果存在，求出最大面积，并指出此时P 点的坐标；如果不存在，请简要说明理由．1．甲、乙两人进行羽毛球比赛，甲发出一枚十分关键的球，出手点为P ，羽毛球飞行的水平距离s （米）与其距地面高度h （米）之间的关系式为23321212++-=s s h ．如图，已知球网AB 距原点5米．乙（用线段CD 表示）扣球的最大高度为94米，设乙的起跳点C 的横坐标为m ，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失误，则m 的取值范围是__________．2．已知x ，y ，z 为实数，若zx yz xy x z z y y x ++=+=+=+则,2,2,1222222的最小值为__________．3．某饮料厂为了开发新产品，用A 、B 两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：（1）假设甲种饮料需配制x 千克，请你写出满足题意的不等式组，并求出其解集；（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y 元，请写出y 与x 的函数表达式．并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额最少？4．某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量y （万件）与销售单价x （元）之间存在着如图所示的一次函数关系．（1）求y 关于x 的函数关系式；（2）试写出该公司销售该种产品的年获利z （万元）关于销售单价x （元）的函数关系式（年获利一年销售额一年销售产品总进价一年总开支）．当销售单价x 为何值时，年获利最大？并求这个最大值；（3）若公司希望该种产品一年的销售获利不低于40万元，借助（2）中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？5．某企业信息部进行市场调研发现：信息一：如果单独投资A 种产品，则所获利润y A （万元）与投资金额x （万元）之间存在正比例函数关系：y A =kx ，并且当投资5万元时，可获利润2万元；信息二：如果单独投资B 种产品，则所获利润y B （万元）与投资金额x （万元）之间存在二次函数关系：y B =ax 2+bx ，并且当投资2万元时，可获利润2.4万元；当投资4万元时，可获利润3.2万元．（1）请分别求出上述的正比例函数表达式与二次函数表达式；（2）如果企业同时对A 、B 两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少．6．已知实数a 、b 、c 满足6,0222=++=++c b a c b a ，则a 的最大值为_____________．7．若正数x 、y 、z 满足))((,4)(z y y x yz x xyz ++=+则的最小可能值为____________．8．函数4)4(1)(22+-++=x x x f 的最小值是____________．9．a 、b 是正数，并且抛物线b ax x y 22++=和a bx x y ++=22都与x 轴有公共点，则22b a +的最小值是____________．10．销售某种商品，如果单价上涨m ％，则售出的数量就将减少150m ，为了使该商品的销售总金额最大，那么m 的值应该确定为____________．11．已知x 、y 、z 为实数，且3,5=++=++zx yz xy z y x ，试求x 的最大值与最小值．12．有一种产品的质量可分成6种不同的档次．若工时不变，每天可生产最低档次的产品40件；如果每提高一个档次，每件利润可增加1元，但每天要少生产2件产品．（1）若最低档次的产品每件利润16元时，生产哪一种档次的产品的利润最大？（2）若最低档次的产品每件利润22元时，生产哪一种档次的产品的利润最大？（3）由于市场价格浮动，生产最低档次产品每件利润可以从8元到24元不等，那么，生产哪种档次的产品所得利润最大？13．如图，在直角坐标系中，以点A （3，0），以23为半径的圆与x 轴相交于点B 、C ，与y 轴相交于点D 、E ．（1）若抛物线c bx x y ++=231经过C 、D 两点，求抛物线的解析式，并判断点B 是否在该抛物线上；（2）在（1）中的抛物线的对称轴上求一点P ，使得△PBD 的周长最小；（3）设Q 为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M ，使得四边形BCQM 是平行四边形？若存在，求出点M 的坐标；若不存在，说明理由．。

九年数学竞赛试题一、选择题(每小题7分，共42分)1.在直角坐标系中，若一点的纵、横坐标都是整数，则称该点为整点.设k 为整数，当直线y=x-2与y=kx+k的交点为整点时，k的值可以取( )(A)4个(B)5个(C)6个(D)7个2.如图，AB是⊙O的直径，C为AB上的一个动点(C点不与A、B重合)，CD⊥AB，AD、CD分别交⊙O于E、F，则与AB·AC相等的一定是( )(A)AE·AD(B)AE·ED(C)CF·CD(D)CF·FD3.在△ABC与△A′B′C′中，已知AB＜A′B′，BC＜B′C′，CA＜C′A′.下列结论：(1)△ABC的边AB上的高小于△A′B′C′的边A′B′上的高；(2)△ABC的面积小于△A′B′C′的面积；(3)△ABC的外接圆半径小于△A′B′C′的外接圆半径；(4)△ABC的内切圆半径小于△A′B′C′的内切圆半径.其中，正确结论的个数为( )(A)0 (B)1 (C)2 (D) 44.设，那么S与2的大小关系是( )(A)S=2 (B)S＜2(C)S＞2 (D)S与2之间的大小与x的取值有关5.折叠圆心为O、半径为10cm的圆纸片，使圆周上的某一点A与圆心O重合.对圆周上的每一点，都这样折叠纸片，从而都有一条折痕.那么，所有折痕所在直线上点的全体为( )(A)以O为圆心、半径为10cm的圆周(B)以O为圆心、半径为5cm的圆周(C)以O为圆心、半径为5cm的圆内部分 (D)以O为圆心，半径为5cm的圆周及圆外部分6.已知x，y，z都是实数，且x2+y2+z2=1，则m=xy+yz+zx( )(A)只有最大值 (B)只有最小值(C)既有最大值又有最小值 (D)既无最大值又无最小值二、填空题(每小题7分，共56分)7.如图是一个树形图的生长过程，依据图中所示的生长规律，第15行的实心圆点的个数等于______.8.如图3，在△ABC中，AD是BC边上的中线，M是AD的中点，CM的延长线交AB于N，则AN:AB的值为______.9.如图，取一张长方形纸片，它的长AB=10cm，宽BC=5cm，然后以虚线CE(E点在AD上)为折痕，使D点落在AB边上.则AE=_____cm，∠DCE=______°.10.如图4，BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，若AD:DB=2:3，AC=10，sinB的值为_____11.直角三角形ABC中，∠A=90°，AB=5cm，AC=4cm，则∠A的平分线AD的长为______cm.12.如图，⊙C通过原点，并与坐标轴分别交于A，D两点.已知∠OBA=30°，点D的坐标为(0,2)，则点A，C的坐标分别为A( , )；C( , ).13.若关于x的方程rx2-(2r+7)x+(r+7)=0的根是正整数，则整数r的值可以是______.14.将2,3,4,5,…,n(n为大于4的整数)分成两组，使得每组中任意两数之和都不是完全平方数.那么，整数n可以取得的最大值是______.三、解答题(每题13分，共52分)15.九年(1)班尚剩班费m(m为小于400的整数)元，拟为每位同学买1本相册.某批发兼零售文具店规定：购相册50本起可按批发价出售，少于50本则按零售价出售，批发价比零售价每本便宜2元，班长若为每位同学买1本，刚好用完m元；但若多买12本给任课教师，可按批发价结算，也恰好只要m元.问该班有多少名同学？每本相册的零售价是多少元？16.已知关于x的方程x2+4x+3k-1=0的两个实根的平方和不小于这两个根的积；反比例函数的图像的两个分支在各自的象限内，点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.17.某中学预计用1500元购买甲商品x个，乙商品y个，不料甲商品每个涨价1.5元，乙商品每个涨价1元，尽管购买甲商品的个数比预定减少10个，总金额多用29元.又若甲商品每个只涨价1元，并且购买甲商品的数量只比预定数少5个，那么买甲、乙两商品支付的总金额是1563.5元.(1)求x、y的关系式；(2)若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205，但小于210，求x，y的值.18.如图，在△ABC中，BC=6，AC=4，∠C=45°，P为BC上的动点，过P作PD∥AB交AC于点D，连结AP，△ABP、△APD、△CDP的面积分别记为S1，S2，S3，设BP=x.(1)试用x的代数式分别表示S1，S2，S3；(2)当P点位于BC上某处使得△APD的面积最大时，你能得出S1、S2、S3之间或S1、S2、S3两两之间的哪些数量关系(要求写出不少于3条)？九年数学竞赛试题答案一、选择题1.A2.A3.A4.D5.D6.C二、填空题7.377 8.1:39.，30 10.11.12.(,0)，(,1) 13.0，1或7 14.2815.设该班共有x名同学，相册零售价每本y元.由题设，得xy=(x+12)(y-2)，①且整数x满足38＜x＜50.②由①得12y-2x-24=0，y=+2，xy=+2x.③由③及xy=m为整数，知整数x必为6的倍数，再由②，x只可能为42或48.此时相应的y为9或10.但m＜400，∴x=42，y=9.答：(略).16.由题意，方程x2+4x+3k-1=0①有实数根，故△=42-4(3k-1)≥0，解之，得k≤.②设x1，x2为①的根，由根与系数关系知x1+x2=-4，x1·x2=3k-1，因≥x1x2，故(x1+x2)2-3x1x2≥0，即(-4)2-3(3k-1)≥0，∴k≤.③又由当x＞0或x＜0时，分别随x值增大而减小，知1+5k＞0，即k＞-.④综合②③④，得-＜k≤.∴满足题中条件的k可取整数值为0, 1.17.(1)设预计购买甲、乙商品的单价分别为a元和b元，则原计划是：ax+by=1500，①由甲商品单价上涨1.5元，乙商品单价上涨1元，并且甲商品减少10个情形，得：(a+1.5)(x-10)+(b+1)y=1529.②再由甲商品单价上涨1元，而数量比预计数少5个，乙商品单价上涨仍是1元的情形得：(a+1)(x-5)+(b+1)y=1563.5.③由①，②，③得：④-⑤×2并化简，得x+2y=186.(2)依题意有：205＜2x+y＜210及x+2y=186.得54＜y＜.由于y是整数，得y=55，从而得x=76.答：略.18.(1)由题意知：BP=x，0＜x＜6，且有，故AD=·BP=x=x.过P作PM⊥AC交AC于M点，过A作AN⊥BC交BC于N点，则PM=PC·sinC=(BC-PB)sin45°=(6-x)，S2=S△APD=AD·PM=·x·(6-x)=2x-x2；又AN=AC·sinC=4·sin45°=4，故S1=S△ABP=BP·AN=2x；S3=S△CDP=CD·PM=(AC-AD)·PM=(4-x)·(6-x)=(6-x)2.(2)因为S2=2x-x2=3-(x-3)2，所以当x=3时，S2取最大值S2=3，此时S1=6，S3=3，因此，S1，S2，S3之间的数量关系有S1=S2+S3，S2=S3，S1=2S2，S1=2S3.(以上4个关系只要写出3个即可)。

全国九年级数学竞赛《代数式》专题大全（竞赛真题强化训练）一、单选题1．（2021·全国·九年级竞赛）3535+- ）． A 10B 2C 5D ．22．（2021·全国·九年级竞赛）已知12,12m n ==22(714)(367)8m m a n n -+⋅--=，则a 的值等于（ ）． A ．5-B ．5C ．9-D ．93．（2021·全国·九年级竞赛）设a ，b ，c 的平均数是M ，a ，b 的平均数是N ，N 与c 的平均数是P ．若a b c >>，则M 与P 的大小关系是（ ）． A ．M P =B ．M P >C ．M P <D ．不能确定4．（2021·全国·九年级竞赛）设644686681088101009898100S =+++++S =（ ）A ．15B 52C 72D 72-二、填空题5．（2021·全国·九年级竞赛）计算2222004200312004200220042004+=+______．6．（2021·全国·九年级竞赛）计算321.3450.345 2.69 1.345 1.3450.345⨯⨯--⨯=____．7．（2021·全国·九年级竞赛）实数,x y 满足21,2540x y x xy x y ≥≥--++=，则x y +=_______． 8．（2021·全国·九年级竞赛）已知32323232x y -+=+-，那么22y x x y +=_______．9．（2021·全国·九年级竞赛）92939899929398a a aa a a a a a aa a+=++++__，其中0a >．10．（2021·全国·九年级竞赛）若实数,,x y z 满足371,4102005x y z x y z ++=++=，则分式3200420042004x yx y z+++值为__________．11．（2021·全国·九年级竞赛）已知3131a -=+4325654a a a a -+-+=________． 12．（2021·全国·九年级竞赛）计算1111068178288961028++++=⨯+⨯+⨯+⨯+___________．13．（2021·全国·九年级竞赛） 1511914117111234567892612203042567290-+-+-+-+=_______．三、解答题14．（2021·全国·九年级竞赛）某同学计算2222244()244x x x x x x x --+÷+--其中“2006x =，时把“2006x =错抄成“2006x ，但他的计算结果仍是正确的，请你说明这是为什么?15．（2021·全国·九年级竞赛）计算3331999100099919991000999--⨯⨯．16．（2021·全国·九年级竞赛）已知1111111112581120411101640+++++++=，求111111112581120411101640---+--++的值． 17．（2021·全国·九年级竞赛）分解因式：22223273x xy y xz yz z ---+-． 18．（2021·全国·九年级竞赛）分解因式：2222()(3)2a b x c a b x c -++-． 19．（2021·全国·九年级竞赛）分解因式：33(1)(3)4(35)x x x +++-+． 20．（2021·全国·九年级竞赛）分解因式：42199619951996x x x +++． 21．（2021·全国·九年级竞赛）分解因式：4224x x y y ++．22．（2021·全国·九年级竞赛）分解因式：222222()()x x a a x a x a ++++． 23．（2021·全国·九年级竞赛）分解因式：2()4()()c a b c a b ----． 24．（2021·全国·九年级竞赛）分解因式：3223x x xy y y ----．25．（2021·全国·九年级竞赛）分解因式：2222x yz axyz yz xy xz az ++---． 26．（2021·全国·九年级竞赛）分解因式：54323331x x x x x -+---+．27．（2021·全国·九年级竞赛）分解因式：()22223()(2)6()(2)3()2x y a b m n xy a b m n xy a b m n ++-++++⋅+．28．（2021·全国·九年级竞赛）比较两数20082009491491A +=+与20092010491491B +=+的大小29．（2021·全国·九年级竞赛）若,,a b c 为整数且99991a bc a-+-=，求c a a b b c -+-+-的值．30．（2021·全国·九年级竞赛）若0a b c abc ++=≠，计算222222(1)(1)(1)(1)(1)(1)b c c a a b bc ca ab ------++的值． 31．（2021·全国·九年级竞赛）已知有理数,,a b c 均不为0，且0a b c ++=，设a b c x b cc aa b=+++++，试求代数式19992000x x -+的值． 32．（2021·全国·九年级竞赛）计算：199719992001(19971999)(19972001)(19992001)(19991997)(20011997)(20011999)------．33．（2021·全国·九年级竞赛）计算：999998998999998999999998⨯-⨯． 34．（2021·全国·九年级竞赛）若56789012345678901235,67890123456789012347A B ==，试比较A 与B 的大小．35．（2021·全国·九年级竞赛）计算444444444411111135989944444111112469910044444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值． 36．（2021·全国·九年级竞赛）计算下列分式的值：(252)(472)(692)(8112)(199419972)(142)(362)(582)(7102)(199319962)⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+．37．（2021·全国·九年级竞赛）已知代数式31519972ax by ++=，当2x =时，4y =-；当14,2x y =-=-时，求代数式33244986ax by -+的值． 38．（2021·全国·九年级竞赛）计算： （1）2222123n +++⋯+； （2）3333123n +++⋯+．39．（2021·全国·九年级竞赛）计算： （1）()1223341n n ⨯+⨯+⨯+⋯++；（2）()123234345()12n n n ⨯⨯+⨯⨯+⨯⨯+⋯+++． 40．（2021·全国·九年级竞赛）如果2|2|(2)0a ab -+-=，求1111(1)(1)(2)(2)(2006)(2006)ab a b a b a b ++++++++++的值．41．（2021·全国·九年级竞赛）计算22222222123991100500022005000330050009999005000++++=-+-+-+-+_________．42．（2021·全国·九年级竞赛）若21321n n a a a a a a d --=-==-=，则称12,,,n a a a …是等差数列，d 叫的公差．证明：（1）()11n a a n d +-=；① （2）1121()1(1)22n n n a a a a a na n n d ++++==+-．② 43．（2021·全国·九年级竞赛）分解因式：32222()()()3a b c a a c b a b c abc +-+-++-． 44．（2021·全国·九年级竞赛）分解因式：32()2772f x x x x =-+-． 45．（2021·全国·九年级竞赛）分解因式：2231032x xy y x y --++-．46．（2021·全国·九年级竞赛）在实数范围内分解因式：()()()()11359x x x x -+++-． 47．（2021·全国·九年级竞赛）分解因式：222222444222a b b c c a a b c ++---．48．（2021·全国·九年级竞赛）分解因式：22242(1)2(1)(1)y x y x y +-++-．49．（2021·全国·九年级竞赛）分解因式：()()()()23222336x y x y y x y x x y -++---+． 50．（2021·全国·九年级竞赛）分解因式：4444444()()()()a b c a b b c c a a b c ++-+-+-++++．竞赛专题2 代数式解析一、单选题1．（2021·全国·九年级竞赛）3535+- ）． A 10B 2C 5D ．2【答案】B 【解析】 【分析】 【详解】解法一 设3535x =+-2(35)2(35)(35)(35)6222x =-+-=-⨯=．解法二 原式62562522+-=222(5)251(5)25122++-+=22(51)(51)22+-=5151222+-=故选：B ．2．（2021·全国·九年级竞赛）已知12,12m n ==22(714)(367)8m m a n n -+⋅--=，则a 的值等于（ ）． A ．5- B ．5C ．9-D ．9【答案】C 【解析】 【分析】 【详解】解：()2212,21m m m -=∴-=．又22(1)2,21n n n -=-=，所以()()7378a +-=，即9a =-．故选：C ．3．（2021·全国·九年级竞赛）设a ，b ，c 的平均数是M ，a ，b 的平均数是N ，N 与c 的平均数是P ．若a b c >>，则M 与P 的大小关系是（ ）． A ．M P = B ．M P >C ．M P <D ．不能确定【答案】B 【解析】 【分析】 【详解】 解 依题意2,,3224a b c a b N c a b c M N P ++++++====，2()()1212a b c a c b c M P +--+--==． 因a b c >>，故0M P ->，即M P >．故应选B 4．（2021·全国·九年级竞赛）设644686681088101009898100S =+++++S =（ ）A ．15B 52C 72D 72-【答案】A 【解析】 【分析】 【详解】 (2)2n n n n +++(2)(2)n n n n +++22(2)n nn n+-=+1(),4,6,8,,10022n n n ==⋯+， 所以112466881098100S ⎡⎤⎛=++++⎢⎥ ⎝⎣⎦124100=1111()22105=-=． 故选：A ． 二、填空题5．（2021·全国·九年级竞赛）计算2222004200312004200220042004+=+______． 【答案】12 【解析】 【分析】 【详解】解：令20042003a =，则原式22222111(1)(1)2(1)2a a a a a ++===-+++．故答案为：12．6．（2021·全国·九年级竞赛）计算321.3450.345 2.69 1.345 1.3450.345⨯⨯--⨯=____． 【答案】 1.345- 【解析】 【分析】 【详解】解：令 1.345,0.345a b ==，则1a b -=．于是，原式32222(2)a b a a ab a a ab b =⨯⨯--=--+ 2() 1.345a a b a =--=-=-．故答案为： 1.345-．7．（2021·全国·九年级竞赛）实数,x y 满足21,2540x y x xy x y ≥≥--++=，则x y +=_______． 【答案】4 【解析】 【分析】 【详解】解：因1x y ≥≥，由题意得222254(1)(1)440(2)0x x y x x x x x x -+=-≤-⇒-+≤⇒-≤．又2(2)0x -≥，从而2x =．代入2254(1)x x y x -+=-得2y =，所以4x y +=． 故答案为：4．8．（2021·全国·九年级竞赛）已知32323232x y -+=+-，那么22y x x y +=_______．【答案】970 【解析】【详解】解：因为221,(32)(32)10xy x y =+=+=，所以 332222y x y x x y x y ++= 222()()()x y x xy y xy +-+=22()()3()x y x y xy xy ⎡⎤++-⎣⎦=221010311⎡⎤-⨯⎣⎦=970=．故答案为：970．9．（2021·全国·九年级竞赛）92939899929398a a aa a a a a a aa a+=++++__，其中0a >．【答案】4 【解析】 【分析】 【详解】 解：令18a x 则原式24616294969169x x x x x x x x x x x x =++++++++ 357753357111111111111x x x x x x x x x x x x =+++++++++++++++ 753775533111111111111x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=+++++++ ⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭11114=+++=．故答案为：4．10．（2021·全国·九年级竞赛）若实数,,x y z 满足371,4102005x y z x y z ++=++=，则分式3200420042004x yx y z +++值为__________．【答案】14007- 【解析】 【分析】解：由题意得方程组2(3)()1,3(3)()2005,x y x y z x y x y z ++++=⎧⎨++++=⎩解出32004,4007,x y x y z +=⎧⎨++=-⎩所以3312004200420042004()4007x y x y x y z x y z ++==-++++．故答案为：14007-． 11．（2021·全国·九年级竞赛）已知3131a -=+4325654a a a a -+-+=________． 【答案】3 【解析】 【分析】 【详解】解：因231(31)2331a --===+22(2)(3)a -=，即2410a a -+=，于是，应用带余除法得432225654(41)(1)33a a a a a a a a -+-+=-+-++=．故答案为：3．12．（2021·全国·九年级竞赛）计算1111068178288961028++++=⨯+⨯+⨯+⨯+___________．【答案】805119800【解析】 【分析】 【详解】 解:因为[]2(4)(2)1111(6)868(2)(4)2(2)(4)a a a a a a a a a a +-+===⋅=++++++++111()(0,1,2,,96)224a a a -=++，所以原式111111111111111()()()()()2242352462969829799=-+-+-++-+-11111111149328051()()()2981002239910021009919800+-=+--=+=． 故答案为：805119800． 13．（2021·全国·九年级竞赛） 1511914117111234567892612203042567290-+-+-+-+=_______．【答案】9110【解析】【详解】 解:原式111111111(1)(3)(3)(5)(5)(7)(7)(9)(9)2612203042567290=+--++--++--++--++11111111112612203042567290=+++++++++11111111111223344556677889910=+++++++++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 111111111111111111(1)()()()()()()()()223344556677889910=+-+-+-+-+-+-+-+-+-191111010=+-=． 故答案为：9110． 三、解答题14．（2021·全国·九年级竞赛）某同学计算2222244()244x x x x x x x --+÷+--其中“2006x =，时把“2006x =错抄成“2006x ，但他的计算结果仍是正确的，请你说明这是为什么? 【答案】见解析． 【解析】 【分析】 【详解】解：令2,2a x b x =+=-，则2222,4,44a b x x ab x x b +=-=-=-，于是 原式222224()441()()()b b a b ab a ab ab ab a b a b x -+=+÷=⨯==++．故把“2006x =错写成“2006x =了，计算结果仍然是正确的．15．（2021·全国·九年级竞赛）计算3331999100099919991000999--⨯⨯．【答案】3． 【解析】 【分析】 【详解】解：设1999,1000a b ==，则原式222333()()()()33()()a b a ab b a b a b a b ab ab a b ab a b ab⎡⎤-++-----⎣⎦====--．16．（2021·全国·九年级竞赛）已知1111111112581120411101640+++++++=，求111111112581120411101640---+--++的值． 【答案】131164-． 【解析】 【分析】 【详解】解：记111111112581120411101640a =---+--++，则11111111111111111()()25811204111016402581120411101640a +=---+--++++++++++222221111101640110820=++=+ 211653310820820164=+==， 331311164164a ∴=-=-． 故所求原式的值为131164-． 17．（2021·全国·九年级竞赛）分解因式：22223273x xy y xz yz z ---+-． 【答案】()()232x y z x y z +--+ 【解析】 【分析】 【详解】解 因为所以，原式()()232x y z x y z =+--+．18．（2021·全国·九年级竞赛）分解因式：2222()(3)2a b x c a b x c -++-．【答案】[]2222()(3)2()2[()]a b x c a b x c a b x c a b x c -++-=-++-【解析】 【分析】 【详解】解 因为()2a b c-()()2()()(3)a b ca b c c a b c a b +-+⋅+-⋅-=+所以[]2222()(3)2()2[()]a b x c a b x c a b x c a b x c -++-=-++-．19．（2021·全国·九年级竞赛）分解因式：33(1)(3)4(35)x x x +++-+． 【答案】22(4)(1)x x ++ 【解析】 【分析】 【详解】 解 令(1)(3)22x x y x +++==+，则原式[]33(1)(1)43(2)5y y y =-++--+3264(31)y y y =+-- 32(32)y y =-+332[(2)3(2)]y y =+-+22[(2)(24)3(2)]y y y y =+-+-+ 22(2)(21)y y y =+-+ 22(2)(1)y y =+- 22(4)(1)x x =++．20．（2021·全国·九年级竞赛）分解因式：42199619951996x x x +++． 【答案】22(1)(1996)x x x x ++-+ 【解析】 【分析】 【详解】解 设1996a =，则19951a =-，于是 原式4242(1)(1)x ax a x a x x a x x =++-+=-+++ 22(1)(1)(1)x x x x a x x =-+++++2(1)[(1)]x x x x a =++-+22(1)(1996)x x x x =++-+．21．（2021·全国·九年级竞赛）分解因式：4224x x y y ++． 【答案】2222()()x xy y x xy y ++-+ 【解析】 【分析】 【详解】解 为了能使用公式2222()aab b a b ++=+，我们将中间项22x y 拆成22222x y x y -，于是原式22222222()2()x x y y x y =++- 2222()()x y xy =+-2222()()x xy y x xy y =++-+．22．（2021·全国·九年级竞赛）分解因式：222222()()x x a a x a x a ++++． 【答案】222()x ax a ++ 【解析】 【分析】 【详解】解法一 原式222222[()()]x x a a x a a x =++++ 22222()()x a x a a x ++=+ 222222()(2)x a x ax a a x =++++ 222222()2()()x a ax x a ax =++++ 222()x a ax =++ 222()x ax a =++．解法二 原式22222[()]()x x a a a x a =++++ 22222(22)()x x ax a a x a =++++ 2222()2()[()]x x a x a a x a =++++⋅ 22[()]x a x a =++ 222()x ax a =++．23．（2021·全国·九年级竞赛）分解因式：2()4()()c a b c a b ----． 【答案】2(2)a c b +- 【解析】 【分析】 【详解】解法一 原式222(2)4()c ca a ab b ac bc =-+---+ 222(2)(44)4c ca a ab bc b =++-++ 22()4()(2)a c b a c b =+-++ 2(2)a c b =+-．解法二 原式2[()()]4()()c b a b c b a b =---+-- 22()2()()()4()()c b c b a b a b c b a b =----+-+--22()2()()()c b c b a b a b =-+--+- 2[()()]c b a b =-+- 2(2)a c b =+-．24．（2021·全国·九年级竞赛）分解因式：3223x x xy y y ----． 【答案】22()(1)x xy y x y ++-- 【解析】 【分析】 【详解】解原式3322()()x y x xy y =--++ 2222()()()x y x xy y x xy y =-++-++ 22()(1)x xy y x y =++--．25．（2021·全国·九年级竞赛）分解因式：2222x yz axyz yz xy xz az ++---． 【答案】()()xy z ax xz y -+- 【解析】 【分析】 【详解】解法一 原式2222()()()axyz az x yz xz yz xy =-+-+-()()()az xy z xz xy z y xy z =-+---()()xy z ax xz y =-+-．解法二 原式2222()()x yz axyz xy yz xz az =+-+--()()xy xz az y z xz az y =+--+- ()()xy z xz az y =-+-．26．（2021·全国·九年级竞赛）分解因式：54323331x x x x x -+---+． 【答案】42(31)(1)x x x -+-【解析】 【分析】 【详解】解法一 原式5432(3)(3)(31)x x x x x =-+--- 4(31)(31)(31)x x x x x =-+---- 42(31)(1)x x x =-+-．解法二 原式5342(333)(1)x x x x x =+-+--+ 42423(1)(1)x x x x x =+--+- 42(31)(1)x x x =-+-．27．（2021·全国·九年级竞赛）分解因式：()22223()(2)6()(2)3()2x y a b m n xy a b m n xy a b m n ++-++++⋅+．【答案】()()()32421xy a b m n ax bx my ny +++--+ 【解析】 【分析】 【详解】解 原式()()()()32221xy a b m n x a b y m n =+++-++⎡⎤⎣⎦()()()32421xy a b m n ax bx my ny =+++--+．28．（2021·全国·九年级竞赛）比较两数20082009491491A +=+与20092010491491B +=+的大小【答案】A B > 【解析】 【分析】 【详解】解 设200849n =，则2009201024949,4949n n ==，于是()2222224949111491(1)(491)491491(491)49981n n A n n n n B n n n n n +++++++=÷==>1+++++， 所以A B >．29．（2021·全国·九年级竞赛）若,,a b c 为整数且99991a b c a-+-=，求c a a b b c -+-+-的值．【答案】2，见解析． 【解析】 【分析】 【详解】解：因,,a b c 均为整数，故,a b c a --均为非负整数，由99991a b c a-+-=，只能得0,1a b c a -=-=或者1,0a b c a -=-=．当0,1a b c a -=-=时，,1a b b c a c =-=-=，这时1012c a a b b c -+-+-=++=． 当1,0a b c a -=-=时，,1c a b c b a =-=-=，这时0112c a a b b c -+-+-=++=． 故总有2c a a b b c -+-+-=．30．（2021·全国·九年级竞赛）若0a b c abc ++=≠，计算222222(1)(1)(1)(1)(1)(1)b c c a a b bc ca ab ------++的值． 【答案】4． 【解析】 【分析】 【详解】 解：原式111b c c a a bbc ca ab bc c b ca a c ab b a=--++--++--+ 11()()()c b c c a a b ab bc ca bc ca ab a b c+++=++-+++++． 由0a b c abc ++=≠得1111,1,1,1b c c a a bbc ca ab bc ca ab a b c+++++==-=-=-， 代入上式得原式()()()()11114bc ca ab ab bc ca ⎡⎤⎣=--+-+-+++=⎦．31．（2021·全国·九年级竞赛）已知有理数,,a b c 均不为0，且0a b c ++=，设a b c x b cc aa b=+++++，试求代数式19992000x x -+的值． 【答案】1902． 【解析】 【分析】 【详解】解：因,,a b c 均不为0，且0a b c ++=，故,,a b c 中或两正一负，或两负一正，且,,a b c b c a c a b +=-+=-+=-，所以1a b c x abc=++=---．于是1999200019920001902x x -+=-+=． 32．（2021·全国·九年级竞赛）计算：199719992001(19971999)(19972001)(19992001)(19991997)(20011997)(20011999)------．【答案】0．【分析】 【详解】解：令1997,1999,2001a b c === 原式()()()()()()a b ca b a c b c b a c a c b =++------()()()()()()a b c b a c c a b a b a c b c ---+-=---0()()()ab ac ab bc ac bca b a c b c --++-==---．33．（2021·全国·九年级竞赛）计算：999998998999998999999998⨯-⨯． 【答案】1997 【解析】 【分析】 【详解】解：设999,998a b ==，则1997,1a b a b +=-=，于是原式()()636310101010a b b a b a a b =⨯+⨯+-⨯+⨯+22a b =-()()199711997a b a b =+-=⨯=．34．（2021·全国·九年级竞赛）若56789012345678901235,67890123456789012347A B ==，试比较A 与B 的大小．【答案】A B >，见解析． 【解析】 【分析】 【详解】解：设5678901234,6789012345x y ==，则1(2)(1)202(2)(2)x x x y y x x yA B y y y y y y ++-+--=-==>+++． 所以A B >．35．（2021·全国·九年级竞赛）计算444444444411111135989944444111112469910044444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值． 【答案】120201【解析】 【分析】解：注意到4422222111()()442a a a a a a +=++-=+- 221111()()(1)[(1)]2222a a a a a a a a ⎡⎤=-+++=-+++⎢⎥⎣⎦，于是原式111111011223349899991002222221111111223344599100100101222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯+⨯+⨯+⨯+⨯+⨯+ ⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯+⨯+⨯+⨯+⨯+⨯+ ⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 101121202011001012⨯+==⨯+． 36．（2021·全国·九年级竞赛）计算下列分式的值：(252)(472)(692)(8112)(199419972)(142)(362)(582)(7102)(199319962)⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+．【答案】998． 【解析】 【分析】 【详解】解：注意到()()()3212a a a a ++=++，所以 原式(34)(56)(78)(910)(1112)(19951996)199699811)(19941995)2⨯⨯⨯⨯⨯⨯===⨯⨯．37．（2021·全国·九年级竞赛）已知代数式31519972ax by ++=，当2x =时，4y =-；当14,2x y =-=-时，求代数式33244986ax by -+的值． 【答案】1998． 【解析】 【分析】 【详解】解：当2x =时，4y =-，代入31519972ax by ++=，得821992a b -=，即4996a b -=．所以当14,2x y =-=-时，有3324498612349863(4)4986399649861998ax by a b a b -+=-++=--+=-⨯+=．故所求代数式的值为1998． 38．（2021·全国·九年级竞赛）计算：（1）2222123n +++⋯+； （2）3333123n +++⋯+．【答案】（1）1(1)(21)6n n n ++；（2）2(1)2n n +⎡⎤⎢⎥⎣⎦． 【解析】 【分析】 【详解】解:（1）因为2[(1)1](1)(1,2,),k k k k k k k n =+-=+-=⋯，于是由公式⑦和③得2222123n +++⋯+()()()()1212323431n n n =⨯-+⨯-+⨯-+⋯++-⎡⎤⎣⎦ ()()1223341123n n n ⎡⎤⎣⎦=⨯+⨯+⨯+⋯++-+++⋯+ 11(1)(2)(1)32n n n n n =++-+ []1(1)2(2)36n n n =++- 1(1)(21)6n n n =++， 故22221123(1)(21)6n n n n ++++=++． ⑧（2）因为3[(1)(2)32]k k k k k =++-- ()()()12311k k k k =++-++⎡⎤⎣⎦()()()1231k k k k k k =++-++，于是由公式③和⑦得 3333123n +++⋯+()()()123312123432323453343=⨯⨯-⨯⨯++⨯⨯-⨯⨯++⨯⨯-⨯⨯++⋯()()()1231n n n n n n +++-++⎡⎤⎣⎦[123234345(1)(2)]3[122334(1)](123)n n n n n n =⨯⨯+⨯⨯+⨯⨯++++-⨯+⨯+⨯++++++++111(1)(2)(3)3(1)(2)(1)432n n n n n n n n n =+++-⨯++++ []1(1)(2)(3)4(2)24n n n n n =+++-++ 2221(1)(1)42n n n n +⎡⎤=+=⎢⎥⎣⎦， 或因32[(1)(2)32](1)(2)32k k k k k k k k k k =++--=++--， 于是由公式⑦，⑧和③得 33312n +++()()22212331212343222[(1)(2)22]n n n n n =⨯⨯-⨯-⨯+⨯⨯-⨯-⨯++++-- ()222[123234(1)(2)]3122(12)n n n n n =⨯⨯+⨯⨯++++-+++-+++111(1)(2)(3)3(1)(21)2(1)462n n n n n n n n n =+++-⨯++-⨯+ [](1)(2)(3)2(21)44n n n n n +=⨯++-+- 222(1)(1)42n n n n ++⎡⎤==⎢⎥⎣⎦， 故23333(1)1232n n n +⎡⎤++++=⎢⎥⎣⎦． ⑨ 39．（2021·全国·九年级竞赛）计算： （1）()1223341n n ⨯+⨯+⨯+⋯++；（2）()123234345()12n n n ⨯⨯+⨯⨯+⨯⨯+⋯+++．【答案】（1）1(2)(1)3n n n ++；（2）1(3)(2)(1)4n n n n +++．【解析】 【分析】 【详解】解:（1）因为11(1)[(2)(1)](1)[(1)(2)(1)(1)](1,2,,)33k k k k k k k k k k k k k n +=+--+=++--+=，所以()1223341n n ⨯+⨯+⨯+⋯++[]1111(321210)(432321)(543432)(2)(1)(1)(1)3333n n n n n n =⨯⨯-⨯⨯+⨯⨯-⨯⨯+⨯⨯-⨯⨯++++-+-1(2)(1)3n n n =++． （2）因为()()12k k k ++[]1(3)(1)(1)(2)4k k k k k =+--++ 1[(3)(2)(1)(2)(1)(1)](1,2,,)4k k k k k k k k k n =+++-++-=…， 所以 ()()12323434512n n n ⨯⨯+⨯⨯+⨯⨯+⋯+++ 111(43213210)(54324321)(65435432)444=⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯+[]1(3)(2)(1)(2)(1)(1)4n n n n n n n n ++++-++-1(3)(2)(1)4n n n n =+++． 注：用类似方法可以证明： 123(1)234(1)345(1)k k k k k ⨯⨯⨯⨯-⨯+⨯⨯⨯⨯⨯++⨯⨯⨯⨯+⨯1(2)(1)(2)(1)()(1)211k n n n n k n k n k k ++++++-=⋅+⨯+-⨯⨯⨯+．⑦40．（2021·全国·九年级竞赛）如果2|2|(2)0a ab -+-=，求1111(1)(1)(2)(2)(2006)(2006)ab a b a b a b ++++++++++的值．【答案】20072008【解析】 【分析】 【详解】解: 由()220,20a ab ≥-≥-，且2|2|(2)0a ab -+-=，得2|2|(2)0a ab -=-=，解得2,1a b ==． 又1(2)(1)11((1,2,,2006)()()(2)(1)12k k k k k b k k k k k +-+==-=++++++，所以原式1111111112007()()()()11223342007200820082008=-+-+-++-=-=． 41．（2021·全国·九年级竞赛）计算22222222123991100500022005000330050009999005000++++=-+-+-+-+_________． 【答案】99 【解析】 【分析】 【详解】解：因为2222(100)1005000(100)100(100)5000k k k k k k -+-+---+ 2222222222(100)2100100(100)(100)2100(100)100k k k k k k k k -=+⎡⎤⎡⎤+-⨯+-+--⨯-+⎣⎦⎣⎦ []22222222(100)2(100)(100)(100)100k k k k k k -=+=+--+--． （*） 记22222222129899110050002200500098980050009999005000S =++++-+-+-+-+， 则将S 中求和顺序反过来写有22222222999821999900500098980050002200500011005000S =++++-+-+-+-+，将两式对应项相加，并利用等式（*）得22222221992982110050009999005000220050009898005000S ⎛⎫⎛⎫=+++++ ⎪ ⎪-+-+-+-+⎝⎭⎝⎭22222222982991299989800500022005000999900500011005000⎛⎫⎛⎫+++=⨯ ⎪ ⎪-+-+-+-+⎝⎭⎝⎭， 所以99S =．故答案为：9942．（2021·全国·九年级竞赛）若21321n n a a a a a a d --=-==-=，则称12,,,n a a a …是等差数列，d 叫的公差．证明：（1）()11n a a n d +-=；①（2）1121()1(1)22n n n a a a a a na n n d ++++==+-．② 【答案】（1）见解析；（2）见解析．【解析】【分析】【详解】证明：（1）()()()112132111(1)n n n n a a a a a a a a a d d d a n d --=+-+-++-=++++=+-个．（2）因为111(1),()k n k a a k d a a n k d +-=+-=+-，故1111(1)()2(1)(1,2,3,,)k n k a a a k d a n k d a n d k n +-+=+-++-=+-=．令121n n n S a a a a -=++++，又将和式中顺序反过来写有121n n n S a a a a -=++++．两式对应项相加，并利用121321n n n n a a a a a a a a --+=+=+==+得()()()()()12132112n n n n n n S a a a a a a a a n a a --=++++++++=+， 所以[]1111()11(1)(1)222n n n a a S n a a n d na n n d +==++-=+-． 注：在②中令k a k =或()211,2,,k a k k n =-=⋯，我们分别得到(1)1232n n n +++++=③ 2135(21)n n ++++-=④公式②、③、④在许多求和问题中要用到，应当记住这些公式．43．（2021·全国·九年级竞赛）分解因式：32222()()()3a b c a a c b a b c abc +-+-++-．【答案】()()()a b a c a b c +-+-【解析】【分析】【详解】解 将题中多项式看成a 的多项式，记为()f a ，并按a 的降幂整理为：322222()2()(3)f a a b c a b bc c a b c bc =+-+-+-+．因为322222()2()(3)0f b b b c b b bc c b b c bc -=-+---+-+=，故()f a 有因式a b +．由综合除法： 2222222212()32120b c b bc c b c bc b bb bc b c bc b c bc c --+-+---+---+ 所以2()()(2)()()()()f a a b a b c a c b c a b a c a b c ⎡⎤=++---=+-+-⎣⎦．1c -1()2b cc b c b c--+-=-44．（2021·全国·九年级竞赛）分解因式：32()2772f x x x x =-+-．【答案】(1)(21)(2)x x x ---【解析】【分析】【详解】解 若()0q f p =，则()f x 有因式q x p-，且p 只可能为3x 系数2的因数：1,2,q ±±只能是常数项2-的因数：1,2±±，故q p 只可能为11,2,2±±±．又()127720f =-+-=，于是1是()f x 的一个根，从而1x -是()f x 的一个因式．由综合除法：277212522520---- 故2()(1)(252)(1)(21)(2)f x x x x x x x =--+=---．21-121(1)(2)25-⨯-+-⨯=-45．（2021·全国·九年级竞赛）分解因式：2231032x xy y x y --++-．【答案】()()5221x y x y --+-【解析】【分析】【详解】解 先用十字相乘法对22310x xy y --分解因式：因为（Ⅰ）15-1(5)23121⨯-+⨯=-所以22310(5)(2)x xy y x y x y --=-+，于是原式()()5232x y x y x y =-+-++．又因为（Ⅱ）52x y --21(2)(2)(1)(5)3x y x y x y x y +--++--=-+（上式中x 与y 不能省略．）所以，原式()()5221x y x y =--+-．注：（1）例20中我们连续两次用了十字相乘法，故这种分解二元二次多项式的因式的方法又叫做双十字相乘法．（2）例20中若令0x =（或0y =），可得2102(52)(21)y y y y -++=---[或232(2)(1)x x x x -+=--]．此式可用十字相乘法求出：（Ⅲ）52--222(2)(1)(5)1-⨯-+-⨯-=()12111(2)1(1)3⎛ - - ⨯-+⨯-=-⎝或Ⅲ＇故也可由（Ⅰ）、（Ⅲ）（或（Ⅰ）、（Ⅲ′））得出原式的因式分解，且（Ⅰ）、（Ⅲ）[或（Ⅰ）、（Ⅲ′）]可合并写成一个算式：46．（2021·全国·九年级竞赛）在实数范围内分解因式：()()()()11359x x x x -+++-． 【答案】2(2)(210)(210)x x x +++【解析】【分析】【详解】解 原式()()()()15139x x x x =-+++⎡⎤⎡⎤⎣⎦⎣-⎦22(45)(43)9x x x x =+-++-． 设222(45)(43)412x x x x y x x +-+++==+-，则 原式()()449y y =-+-2216925y y =--=-()()55y y =+-22(44)(46)x x x x =+++-22(2)(2)10x x ⎡⎤=++-⎣⎦2(2)(210)(210)x x x =+++．47．（2021·全国·九年级竞赛）分解因式：222222444222a b b c c a a b c ++---．【答案】()()()()a b c b c a c a b a b c +++-+-+-【解析】【分析】【详解】解法一 以a 为主元降幂排列，再配方得：原式422244222()(2)a b c a b c b c -++-+=-4222222222222[2()()]()()a b c a b c b c b c =--+++++--222222222222[()][()()][()()]a b c b c b c b c b c =--++++-+--22222(2)()bc a b c =---222222[2()][2()]bc a b c bc a b c =---+--2222[()][()]b c a a b c =+---()()()()b c a b c a c a b a b c =+++-+-+-．解法二 原式42244222(2)2()a a b b c a b c =--+-++222222222222[()2()]2()2()a b a b c c a b c a b c '=--+-++-++222222()4a b c a c =--++222222(2)(2)ac a b c ac a b c =+-+-+-2222[()][()]a c b b a c =+---()()()()a c b a c b b a c b c a =+++-+-+-．解法三 注意到下列公式：2222444222222()222a b c a b c a b a c b c +-=+++--，为了完成整个式子的直接配方，应将222a b 拆成222242a b a b -．原式224442222224(222)a b a b c a b a c b c =-+++--22222(2)()ab a b c =-+-22222(2)(2)ab a b c ab a b c =++---+2222[()][()]a b c c a b =+---()()()()a b c a b c c a b c a b =++-+--+＋()()()()a b c b c a c a b a b c =+++-+-+-．48．（2021·全国·九年级竞赛）分解因式：22242(1)2(1)(1)y x y x y +-++-．【答案】()()()()1111x x xy x y xy x y +--++---【解析】【分析】【详解】解法一 添加22(1)(1)y x y +-，再减去同一项得：原式2242222[(1)2(1)(1)(1)]2(1)(1)2(1)y y x y x y y x y x y =+++-+--+--+22222[(1)(1)]2[(1)(1)]y x y x y y =++---++2222(1)(2)x x y y x =-++-2222(12)(12)x x y y x x x y y x =-+++-++-2222[(1)(1)][(1)(1)]x y x x y x =+-----()()()()()111111x x y x x x y x ⎡⎤⎡⎤⎣⎦=++-----+⎣⎦()()()()1111x x x y xy x y xy =+-++--+--()()()()1111x x x y xy x y xy =+-++--++．解法二 以y 为主元降幂排列．原式422442(21)2(1)(21)x x y x y x x =-+--+-+222222(1)2(1)(1)(1)x y x x y x =---++-22222(1)[(1)2(1)1]x x y x y x =---++-222(1)(1)[(21)(21)]x x x y y y y =+--+-++222(1)(1)[(1)(1)]x x x y y =+---+()()()()()111111x x x y y x y y ⎡=+--++--⎤⎦+⎡⎤⎣⎣⎦ ()()()()1111x x xy x y xy x y =+--++---．49．（2021·全国·九年级竞赛）分解因式：()()()()23222336x y x y y x y x x y -++---+．【答案】()()3221x y x --【解析】【分析】【详解】解 因为()()22,3632y x x y x y x y -=---+=--，所以原式()()()()()23222332x y x y x y y x x y =-+-----()()()232233x y x y y x =-+---⎡⎤⎣⎦()()263x y x =--()()3221x y x =--．50．（2021·全国·九年级竞赛）分解因式：4444444()()()()a b c a b b c c a a b c ++-+-+-++++．【答案】4444444()()()()12()a b c a b b c c a a b c abc a b c ++-+-+-++++=++【解析】【分析】【详解】解 设4444444(,,)()()()()f a b c a b c a b b c c a a b c =++-+-+-++++．因为444444(0,,)0()()0f b c b c b b c c b c =++--+-++=，所以(),,f a b c 有因式a ． 由(),,f a b c 是,,a b c 的四次对称多项式知(),,f a b c 有因式abc ，而(),,f a b c 与abc 分别是四次、三次对称多项式，所以(),,f a b c 还含有,,a b c 的一个一次对称多项式()k a b c ++，即4444444(,,)()()()()f a b c a b c a b b c c a a b c =++-+-+-++++()kabc a b c =++．令1a b c ===，得444444*********k ++---+=，k=，故所以124444444++-+-+-++++=++．a b c a b b c c a a b c abc a b c()()()()12()。

最值问题求法例题（1）、若实数a ，b ，c 满足a2 + b2+ c2= 9，则代数式（a － b）2 + （b —c）2 +（c － a）2的最大值是（）A．27 B、 18 C、15 D、 12例题（2）、如果对于不小于8的自然数N ，当3N+1是一个完全平方数时，N + 1都能表示成K个完全平方数的和，那么K的最小值是（）A、 1B、 2C、 3D、 4例题（3）、设a、b为实数，那么a2＋ab＋b2－a－2b的最小值是——————————。

例题（4）、已知实数a、b满足a2＋ab＋b2=1 ，则a2－ab＋b2的最小值和最大值的和是————————。

例题5、若a、b满足3a＋5∣b∣= 7 ，则S= 2a－3∣b∣的最大值为-------------------，最小值为--------------------。

（二）、直接运用a 2＋b 2≥ 2ab ( a ＋b ≥ 2ab )性质求最值。

例题（6）、若X > 0，则函数Y =3X ＋31X＋21++XX 的最小值。

例题（7）、已知 a 、b 、c 、d 均为实数，且a ＋b ＋c ＋d = 4 ，a 2＋b 2＋c 2＋d 2 =316，求a 的最小值与最大值。

（三）、用一元二次方程根的判别式Δ=b 2－4ac （结合韦达定理）求最值。

例题（8）、已知实数a 、b 、c 满足a ＋b ＋c = 2 ，abc = 4 ，○1求a 、b 、c 中最大者的最小值 ；○2求∣a ∣＋∣b ∣＋∣c ∣的最小值。

例题（9）、求函数Y = 12156322++++X X X X 的最小值。

（四）、用绝对值的几何意义和取零点、分段讨论法求最值。

例题（10）、a b c d e是一个五位自然数，其中a ，b ，c ，d ，e 为阿拉伯数字，且a<b<c<d ,则│a-b │＋│b-c │＋│c －d │＋│d －e │的最大值是 ———。

初三代数竞赛试题及答案一、选择题（每题5分，共20分）1. 若a、b、c为实数，且满足a+b+c=0，下列哪个选项是正确的？A. a^2 + b^2 + c^2 = 0B. ab + bc + ac = 0C. a^2 + b^2 = c^2D. a^3 + b^3 + c^3 = 3abc答案：B2. 已知x、y、z是实数，且x+y+z=1，下列哪个选项是正确的？A. x^2 + y^2 + z^2 ≥ 1/3B. x^2 + y^2 + z^2 ≤ 1/3C. x^2 + y^2 + z^2 = 1/3D. x^2 + y^2 + z^2 < 1/3答案：A3. 若a、b、c是等差数列，且a+b+c=6，下列哪个选项是正确的？A. 2b = a + cB. 3b = a + cC. 2b = 3D. b = 2答案：D4. 已知方程x^2 - 5x + 6 = 0的两个根为x1和x2，下列哪个选项是正确的？A. x1 + x2 = 5B. x1x2 = 6C. x1 + x2 = 6D. x1x2 = 5答案：A二、填空题（每题5分，共20分）5. 若a、b、c是等比数列，且a+b+c=14，b=4，则a和c的值分别为______和______。

答案：2，86. 已知二次函数y=ax^2+bx+c的图象经过点(1,3)和(2,0)，且对称轴为直线x=2，则a的值为______。

答案：-17. 若x、y、z是实数，且x+y+z=3，xy+yz+zx=3，则x^2+y^2+z^2的值为______。

答案：38. 已知方程x^2-6x+5=0的两个根为x1和x2，则(x1-3)(x2-3)的值为______。

答案：-4三、解答题（每题15分，共40分）9. 已知a、b、c是等差数列，且a+c=10，b=5，求a、b、c的值。

解答：由题意可知，a、b、c是等差数列，且a+c=10，b=5。

由于a、b、c是等差数列，所以2b=a+c，即2*5=a+c=10。

【初中数学竞赛】专题02代数式竞赛综合-50题真题专项训练（全国竞赛专用）一、单选题1．（2021·全国·九年级竞赛）已知3a b -=，则339a b ab --的值是（）．A ．3B ．9C ．27D ．81【答案】C 【详解】3322229()()93()9a b ab a b a ab b ab a ab b ab --=-++-=++-22223(2)3()3327a ab b a b =-⨯+=-==．故选C ．2．（2021·全国·九年级竞赛）如果21x x --是31ax bx ++的一个因式，则b 的值是（）．A ．2-B ．1-C ．0D ．23．（2021·全国·九年级竞赛）若223894613M x xy y x y =-+-++（,x y 是实数），则M 的值一定是（）．A ．正数B ．负数C ．零D ．整数【答案】A 【详解】因为22222222(44)(44)(69)2(2)(2)(3)0M x xy y x x y y x y x y =-++-++++=--++≥+，并且2,2,3x y x y --+不能同时等于零，所以0M >．故选A ．4．（2021·全国·）．A ．无理数B ．真分数C ．奇数D ．偶数14=-5．（2021·全国·九年级竞赛）满足等式2003=的正整数对(),x y 的个数是（）．A ．1B ．2C ．3D ．46．（2021·全国·九年级竞赛）已知199919991999200020002000200120012001,,199819981998199919991999200020002000a b c ⨯-⨯-⨯-=-==-⨯+⨯+⨯+，则abc 的值等于（）．A ．1-B ．3C ．3-D ．1故选：D ．二、填空题7．（2021·全国·九年级竞赛）若3233x x x k +-+有一个因式是1x +，则k =_______．【答案】-5【详解】解法一依题意，原多项式当=1x -时，其值等于0，即32(1)3(1)3(1)0k -+---+=，从而5k =-．解法二依题意1x +也是多项式332(1)(33)6(1)x x x x k x k +-+-+=+-的因式，故16k -=，即5k =-．解法三依题意可设()3223233(1)()(1)x x x k x x ax b x a x a b x b+-+=+++=+++++比较同次幂系数得13,2,3,5,, 5.a a a b b k b k +==⎧⎧⎪⎪+=-∴=-⎨⎨⎪⎪==-⎩⎩故5k =-．注：虽然解法三计算量较大，但它的好处是同时求出了原多项式的另一个因式为225x x +-．若题目还要求对原多项式进行因式分解，则解法三是可取的好方法之一．8．（2021·全国·九年级竞赛）设x =，a 是x 的小数部分，b 是x -的小数部分，则333a b ab ++=__________．9．（2021·全国·九年级竞赛）已知x 、y 为正偶数，且2296x y xy +=，则22x y +=__________.【答案】40【分析】根据22x y xy 96+=可知xy(x+y)=96，由x 、y 是正偶数可知xy≥4，x+y≥4，进而可知96可分解成3种乘积的形式，分别计算即可得只有一种情况符合题意，即可求出x 、y 的值，根据x 、y 的值求得答案即可.【详解】∵22x y xy 96+=，∴xy(x+y)=96，∵x 、y 为正偶数，xy≥4，x+y≥4，∴96=2⨯2⨯2⨯2⨯2⨯3=6⨯16=8⨯12=4⨯24当xy(x+y)=4⨯24时，无解，当xy(x+y)=6⨯16时，无解，当xy(x+y)=8⨯12时，x+y=8，xy=12，解得：x=2，y=6，或x=6，y=2，∴x 2+y 2=22+62=40.故答案为40【点睛】本题考查因式分解，把96分解成所有约数的积再分情况求解是解题关键.10．（2021·全国·九年级竞赛）已知对任意正整数n 都有312n a a a n +++= ，则11111111a a a a ++++=---- ___________．三、解答题11．（2021·全国·九年级竞赛）分别在有理数范围内和实数范围内分解因式：4662248365427a a b a b b -+-．12．（2021·全国·九年级竞赛）分解因式：()22223()(2)6()(2)3()2x y a b m n xy a b m n xy a b m n ++-++++⋅+．【答案】()()()32421xy a b m n ax bx my ny +++--+【详解】解原式()()()()32221xy a b m n x a b y m n =+++-++⎡⎤⎣⎦()()()32421xy a b m n ax bx my ny =+++--+．13．（2021·全国·九年级竞赛）分解因式：54323331x x x x x -+---+．【答案】42(31)(1)x x x -+-【详解】解法一原式5432(3)(3)(31)x x x x x =-+---4(31)(31)(31)x x x x x =-+----42(31)(1)x x x =-+-．解法二原式5342(333)(1)x x x x x =+-+--+42423(1)(1)x x x x x =+--+-42(31)(1)x x x =-+-．14．（2021·全国·九年级竞赛）分解因式：2222x yz axyz yz xy xz az ++---．【答案】()()xy z ax xz y -+-【详解】解法一原式2222()()()axyz az x yz xz yz xy =-+-+-()()()az xy z xz xy z y xy z =-+---()()xy z ax xz y =-+-．解法二原式2222()()x yz axyz xy yz xz az =+-+--()()xy xz az y z xz az y =+--+-()()xy z xz az y =-+-．15．（2021·全国·九年级竞赛）分解因式：3223x x xy y y ----．【答案】22()(1)x xy y x y ++--【详解】解原式3322()()x y x xy y =--++2222()()()x y x xy y x xy y =-++-++22()(1)x xy y x y =++--．16．（2021·全国·九年级竞赛）分解因式：2()4()()c a b c a b ----．【答案】2(2)a c b +-【详解】解法一原式222(2)4()c ca a ab b ac bc =-+---+222(2)(44)4c ca a ab bc b =++-++22()4()(2)a c b a c b =+-++2(2)a c b =+-．解法二原式2[()()]4()()c b a b c b a b =---+--22()2()()()4()()c b c b a b a b c b a b =----+-+--22()2()()()c b c b a b a b =-+--+-2[()()]c b a b =-+-2(2)a c b =+-．17．（2021·全国·九年级竞赛）分解因式：222222()()x x a a x a x a ++++．【答案】222()x ax a ++【详解】解法一原式222222[()()]x x a a x a a x =++++22222()()x a x a a x ++=+222222()(2)x a x ax a a x =++++222222()2()()x a ax x a ax =++++222()x a ax =++222()x ax a =++．解法二原式22222[()]()x x a a a x a =++++22222(22)()x x ax a a x a =++++2222()2()[()]x x a x a a x a =++++⋅22[()]x a x a =++222()x ax a =++．18．（2021·全国·九年级竞赛）分解因式：3333a b c abc ++-．【答案】222()()a b c a b c ab ac bc ++++---【详解】解原式33()3()3a b ab a b c abc=+-++-33()3()a b c ab a b c =++-++3[()]3()()3()a b c a b c a b c ab a b c =++-+++-++2()[()3()3]a b c a b c a b c ab =++++-+-222()(222333)a b c a b c ab ac bc ac bc ab =+++++++---222()()a b c a b c ab ac bc =++++---．19．（2021·全国·九年级竞赛）若238x ax bx +++有两个因式1x +和2x +，求a b +的值．所以21a b +=．20．（2021·全国·九年级竞赛）分解因式333(2)()()a b c a b b c ++-+-+．【答案】3()()(2)++++a b b c a b c 【详解】设,A a b B b c =+=+，则原式33333()()[()3()]3()3()()(2)A B A B A B A B AB A B AB A B a b b c a b c =+--=+-+-+=+=++++．21．（2021·全国·九年级竞赛）在实数范围内分解因式：423344x x x x +---．22．（2021·全国·九年级竞赛）分解因式：2()()()()abc bcd cda dab ab cd bc ad ca bd +++----．【答案】2()+++abcd a b c d 【详解】原式是关于a b c d ,,,的对称多项式．若视a 为主元，并以0a =代入得原式0=，故原式有因式a ，由对称性知原式有因式abcd ．又原式是六次齐次多项式，而abcd 是四次齐次多项式，故还有一个关于a b c d ,,,的二次齐次对称多项式因式，所以可设2()()()()abc bcd cda dab ab cd bc ad ca bd +++----2222[()()]abcd A a b c d B ab bc cd da ac bd =+++++++++．令1,1a b c d ====-，得44A -=-；令1a b c d ====，得4616A B +=．所以1,2A B ==．原式2222[()2()]abcd a b c d ab bc cd da ac bd =+++++++++22[()()2()()]abcd a b c d a b c d =++++++2()abcd a b c d =+++23．（2021·全国·九年级竞赛）若122122(1025)(1025)10n +--=，求n 的值．【答案】14【详解】()()()()()()22121212121212102510251025102510251025⎡⎤⎡⎤+--=++-+--⎣⎦⎣⎦12142105010=⨯⨯=，所以41010n =，故14n =．24．（2021·全国·九年级竞赛）设a b c d ,,,是四个整数，且使得2222221()()4m ab cd a b c d =+-+--是一个非零整数，求证：||m 一定是合数．25．（2021·全国·九年级竞赛）若2221995199519961996a ⨯=++，证明：a 是一个完全平方数（即a 等于另一个整数b 的平方）．【答案】见解析【详解】设1995x =，则222222(1)(1)(1)2(1)2(1)a x x x x x x x x x x ⎡⎤=++++=+-+++++⎣⎦2222222(1)[(1)]2(1)(1)12(1)[(1)][1(1)]x x x x x x x x x x x x x x +=+-++++=++++=++=22(119951996)3982021+⨯=，故a 是一个完全平方数．26．（2021·全国·九年级竞赛）设,a b 是实数且422223a b a b =，求22222010a b a b -的值．27．（2021·全国·九年级竞赛）已知a 是正整数，且3221215a a a +-+表示质数，求这个质数．【答案】7【详解】解3221215a a a +-+3225315315a a a a a =+--++2(5)3(5)3(5)a a a a a =+-+++2(5)(33)a a a =+-+．要使2(5)(33)a a a +-+为质数，必须2331a a -+=，即()()210a a --=，故1a =或2．但1a =时，56a +=是合数．只有2a =时，57a +=才是质数．故所求的质数是7．28．（2021·全国·九年级竞赛）分解因式：2(25)(9)(27)91a a a +---．29．（2021·全国·九年级竞赛）证明：对任何整数x 和54322345,3515412y x x y x y x y xy y +--++的值都不等于33．【答案】见解析【详解】解法一原式54322345(3)(515)(412)x x y x y x y xy y =+-+++4224(3)5(3)4(3)x x y x y x y y x y =+-+++4224(3)(54)x y x x y y =+-+2222(3)()(4)x y x y x y =+--()()()()()322x y x y x y x y x y =+-+-+．当0y =时，原式533x =≠；当0y ≠时，3,,,2,2x y x y x y x y x y +-+-+互不相等，而33不可能分解为4个以上不同因数之积，所以0,y x ≠为整数时，原式33≠，所以对,x y 取任何整数值，原式的值都不等于33．解法二将原式看成x 的多项式，y 当成常数，用综合除法有所以，原式()()()()()223x y x y x y x y x y =-+-++．下同解法一．30．（2021·全国·九年级竞赛）设,,a b c 互不相等，且0a b c ++=，化简222222222a b c a bc b ca c ab++．31．（2021·全国·九年级竞赛）分解因式：222222444222a b b c c a a b c ++---．【答案】()()()()a b c b c a c a b a b c+++-+-+-【详解】解法一以a 为主元降幂排列，再配方得：原式422244222()(2)a b c a b c b c -++-+=-4222222222222[2()()]()()a b c a b c b c b c =--+++++--222222222222[()][()()][()()]a b c b c b c b c b c =--++++-+--22222(2)()bc a b c =---222222[2()][2()]bc a b c bc a b c =---+--2222[()][()]b c a a b c =+---()()()()b c a b c a c a b a b c =+++-+-+-．解法二原式42244222(2)2()a a b b c a b c =--+-++222222222222[()2()]2()2()a b a b c c a b c a b c '=--+-++-++222222()4a b c a c =--++222222(2)(2)ac a b c ac a b c =+-+-+-2222[()][()]a cb b ac =+---()()()()a c b a c b b a c b c a =+++-+-+-．解法三注意到下列公式：2222444222222()222a b c a b c a b a c b c +-=+++--，为了完成整个式子的直接配方，应将222a b 拆成222242a b a b -．原式224442222224(222)a b a b c a b a c b c =-+++--22222(2)()ab a b c =-+-22222(2)(2)ab a b c ab a b c =++---+2222[()][()]a b c c a b =+---()()()()a b c a b c c a b c a b =++-+--+＋()()()()a b c b c a c a b a b c =+++-+-+-．32．（2021·全国·九年级竞赛）分解因式：22242(1)2(1)(1)y x y x y +-++-．【答案】()()()()1111x x xy x y xy x y +--++---【详解】解法一添加22(1)(1)y x y +-，再减去同一项得：原式2242222[(1)2(1)(1)(1)]2(1)(1)2(1)y y x y x y y x y x y =+++-+--+--+22222[(1)(1)]2[(1)(1)]y x y x y y =++---++2222(1)(2)x x y y x =-++-2222(12)(12)x x y y x x x y y x =-+++-++-2222[(1)(1)][(1)(1)]x y x x y x =+-----()()()()()111111x x y x x x y x ⎡⎤⎡⎤⎣⎦=++-----+⎣⎦()()()()1111x x x y xy x y xy =+-++--+--()()()()1111x x x y xy x y xy =+-++--++．解法二以y 为主元降幂排列．原式422442(21)2(1)(21)x x y x y x x =-+--+-+222222(1)2(1)(1)(1)x y x x y x =---++-22222(1)[(1)2(1)1]x x y x y x =---++-222(1)(1)[(21)(21)]x x x y y y y =+--+-++222(1)(1)[(1)(1)]x x x y y =+---+()()()()()111111x x x y y x y y ⎡=+--++--⎤⎦+⎡⎤⎣⎣⎦()()()()1111x x xy x y xy x y =+--++---．33．（2021·全国·九年级竞赛）分解因式：4444444()()()()a b c a b b c c a a b c ++-+-+-++++．【答案】4444444()()()()12()a b c a b b c c a a b c abc a b c ++-+-+-++++=++【详解】解设4444444(,,)()()()()f a b c a b c a b b c c a a b c =++-+-+-++++．因为444444(0,,)0()()0f b c b c b b c c b c =++--+-++=，所以(),,f a b c 有因式a ．由(),,f a b c 是,,a b c 的四次对称多项式知(),,f a b c 有因式abc ，而(),,f a b c 与abc 分别是四次、三次对称多项式，所以(),,f a b c 还含有,,a b c 的一个一次对称多项式()k a b c ++，即4444444(,,)()()()()f a b c a b c a b b c c a a b c =++-+-+-++++()kabc a b c =++．令1a b c ===，得444444*********k ++---+=，所以12k =，故4444444()()()()12()a b c a b b c c a a b c abc a b c ++-+-+-++++=++．34．（2021·全国·九年级竞赛）分解因式：444()()()a b c b c a c a b -+-+-．【答案】444()()()a b c b c a c a b -+-+-222()()()()a b b c c a a b c ab bc ca =----+++++．【详解】解设444(,,)()()()f a b c a b c b c a c a b =-+-+-．因为()(),,,,f a b c f b c a =，所以(),,f a b c 是轮换对称多项式．又a b =时，444(,,)()()()0f b b c b b c b c b c b b =-+-+-=，所以(),,f a b c 有因式a b -．又(),,f a b c 是轮换对称多项式，故(),,f a b c 有因式()()()a b b c c a ---．因(),,f a b c 与()()()a b b c c a ---分别是齐五次与齐三次轮换对称多项式，所以(),,f a b c 的另一个因式应是齐二次轮换对称多项式：222()()A a b c B ab bc ca +++++，即444222()()()()()()[()()]a b c b c a c a b a b b c c a A a b c B ab bc ca -+-+-=---+++++．令2,1,0a b c ===及1,0,1a b c ===-，分别得到16202(52),1012(2),A B A B -+=-+⎧⎨++=--⎩即527,21,A B A B +=-⎧⎨-=-⎩解得1A B ==-，故444()()()a b c b c a c a b -+-+-222()()()()a b b c c a a b c ab bc ca =----+++++．35．（2021·全国·九年级竞赛）分解因式：()()()()23222336x y x y y x y x x y -++---+．【答案】()()3221x y x --【详解】解因为()()22,3632y x x y x y x y -=---+=--，所以原式()()()()()23222332x y x y x y y x x y =-+-----()()()232233x y x y y x =-+---⎡⎤⎣⎦()()263x y x =--()()3221x y x =--．36．（2021·全国·九年级竞赛）已知2410a a ++=，且42321322a ma a ma a-+=，求m 的值．37．（2021·全国·九年级竞赛）已知322210a a a +++=，求200920102011a a a ++的值．【答案】-1【详解】()()()32322222112(1)12(1)(1)(a a a a a a a a a a a a a a +++=+++=+-+++=+-+212)(1)(1)0a a a a +=+++=，38．（2021·全国·九年级竞赛）计算444444444411111135989944444111112469910044444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅++ ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值．39．（2021·全国·九年级竞赛）若0a b c abc ++=≠，计算222222(1)(1)(1)(1)(1)(1)b c c a a b bc ca ab------++的值．40．（2021·全国·九年级竞赛）分解因式：555()()()x y y z z x -+-+-．【答案】2225()()()()x y y z z x x y z xy yz zx ---++---【详解】因x y =时，原式0=，故原式有因式x y -．又原式是关于,,x y z 的五次齐次轮换对称多项式，故原式有因式()()()x y y z z x ---，并可设()555222()()()()()()()x y y z z x x y y z z x A x y z B xy yz zx ⎡⎤-+-+-=---+++++⎣⎦．令0,1,1x y z ===-，得()3022A B =-，即215A B -=，再令0,1,2x y z ===，得()30252A B =+，即5215A B +=，解出5,5A B ==-．所以，原式2225()()()()x y y z z x x y z xy yz zx =---++---．41．（2021·全国·九年级竞赛）计算：()()()()222220012007200220082003200920042010(199920035)(199820045)(200120055)(200020065)----⨯-⨯+⨯-⨯+．42．（2021·全国·九年级竞赛）计算：()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++⨯43．（2021·全国·九年级竞赛）计算+44．（2021·全国·九年级竞赛）计算：()()()()()()()()()()44444444441032422324343244632458324432416324283244032452324++++++++++．45．（2021·全国·九年级竞赛）把()()()()16a b c d b c a d c a b d a b c d abcd ++++--+--+--+分解因式．【答案】()()()()a b c d b c d a c d a b d a b c ------------【详解】解法一原式2222[()()][()()]16b c a d a d b c abcd=++---+-22222222(22)(22)16b c a d bc ad a d b c ad bc abcd=+--+-+---++22222222[2()()][2()()]16bc ad b c a d bc ad b c a d abcd =-++----+--+2222224()()16bc ad b c a d abcd=--+--+2222224()()bc ad b c a d =+-+--2222222[2()()][2()()]z bc ad b c a d bc ad b c a d =+++--+-+--2222[()()][()()]b c a d a d b c =+--+--()()()()b c a d b c a d a d b c a d b c =++-+-+++-+-+．解法二把原式看成a 的多项式，当a b c d =++时，原式()()()()()2222160b c d d c b b c d bcd =++-+++=，所以原式有因式a b c d ---．又原式是a b c d ,,,的对称多项式，由对称性知原式有因式()()()()a b c d b c d a c d a b d a b c ------------．又此式和原式都是四次齐次多项式，故()()()()16a b c d b c a d c a b d a b c d abcd++++--+--+--+()()()()k a b c d b c d a c d b a d a b c =------------，其中k 是常数．上式中令1,0a b c d ====得1k -=-，即1k =，所以原式()()()()a b c d b c d a c d a b d a b c =------------．46．（2021·全国·九年级竞赛）已知,b c 是整数，二次三项式2x bx c ++既是42625x x ++的一个因式，也是4234285x x x +++的一个因式，求1x =时2x bx c ++的值．【答案】4【详解】解依题意，2x bx c ++应是424223(625)(34285)14(25)x x x x x x x ++-+++=-+的一个因式，所以2225x bx c x x ++=-+，故当1x =时，22251254x bx c x x ++=-+=-+=．47．（2021·全国·九年级竞赛）把多项式322222422x x x x y xyz xy y z --++-分解因式．【答案】2(2)()x z x y --【详解】解法一原式32222(2)(42)(2)x x z x y xyz xy y z =---+-22(2)2(2)(2)x x z xy x z y x z =---+-22(2)(2)x z x xy y =--+2(2)()x z x y =--．解法二原式32222(242)(2)x x y xy x z xyz y z =-+--+22222(2)(2)x x xy y z x xy y =-+--+222()()x x y z x y =---2(2)()x z x y =--．48．（2021·全国·九年级竞赛）分解因式：2(1)(2)(2)xy x y x y xy -++-+-．【答案】22(1)(1)x y --【详解】解法一原式是关于,x y 的对称多项式．可设,x y u xy v +==，则原式2(1)(2)(2)v u u v =-+--2221242v v u u v uv=-++-+-2222()1u uv v u v =-+--+22()2()1(1)u v u v u v =---+=--222(1)(1)(1)x y xy x y =+--=--．解法二当1x =时，原式2(1)(1)(1)0y y y =-+--=，故原式有因式1x -．又原式是关于,x y 的对称多项式，故原式又有因式1y -，且可设222(1)(2)(2)(1)(1)[()()]xy x y x y xy x y A x y Bxy C x y D -++-+-=--+++++，令0x y ==，得210D +=，得1D =．令0,2x y ==，得210(42)A C D +=-++，即4212A C D +=--=-．令0,3x y ==，得21132(93)A C D +=-++⨯，即9323A C D +=--=-．令2x y ==，得232(4)844A B C D +-=+++⨯，即84410A B C D ++=-=．从上面式子可解出0,1,1,1A B C D ===-=，于是原式()()()111x y xy x y =---++⎡⎤⎣⎦22(1)(1)(1)(1)(1)(1)x y x y x y =----=--．49．（2021·全国·九年级竞赛）分解因式：3333()x y z x y z ++---．【答案】3()()()x y y z z x +++【详解】解法一由公式333()3()a b a b ab a b ±=±± ，得原式3333[()]()x y z z x y =++--+33()3()()[()3()]x y z z x y z z x y z z x y xy x y =++-+++++--+-+()()()33x y x y z z xy x y =+++++()()3x y x y z z xy =++++⎡⎤⎣⎦23()[()]x y z x y z xy =++++()()()3x y z x z y =+++．解法二设3333(,,)()f x y z x y z x y x =++---．将(),,f x y z 看成x 的多项式，令x y =-得3333(,,)()()0f y y z y y z y y z -=-++----=，所以(),,f x y z 有因式x y +．而(),,f x y z 是关于,,x y z 的三次齐次对称多项式，故(),,f x y z 有因式()()()x y y z z x +++，故可设3333(,,)()()()()f x y z x y z x y z k x y y z z x =++---=+++．令1,0x y z ===，得3338110211k ---=⋅⋅⋅，故3k =，所以3333()3()()()x y z x y z x y y z z x ++---=+++．50．（2021·全国·九年级竞赛）分解因式：()()ab bc ca a b c abc ++++-．【答案】()()()()()ab bc ca a b c abc a bb c c a ++++-=+++【详解】解设()()(),,f a b c ab bc ca a b c abc =++++-，当a b =-时，有22(,,)()()0f b b c b bc bc b b c b c -=-+--+++=，所以(),,f a b c 有因式a b +．又因为(),,f a b c 关于,,a b c 对称，故(),,f a b c 还有因式,b c c a ++，即(),,f a b c 有因式()()()a b b c c a +++，并且(),,f a b c 与()()()a b b c c a +++都是齐三次式（各项都是3次的多项式），所以()()()()()(),,f a b c ab bc ca a b c abc k a b b c c a=++++-=+++，其中k 为常数．上式中令1a b ==得3318k ⨯-=，即1k =，所以()()()()()ab bc ca a b c abc a b b c c a ++++-=+++．。

九年级数学中考典型及竞赛训练专题25 平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下，求平面几何图形中某个确定的量（如线段长度、角度大小、图形面积）等的最大值或最小值.求几何最值问题的基本方法有：1.特殊位置与极端位置法：先考虑特殊位置或极端位置，确定最值的具体数据，再进行一般情形下的推证.2.几何定理（公理）法：应用几何中的不等量性质、定理.3.数形结合法等：揭示问题中变动元素的代数关系，构造一元二次方程、二次函数等.例题与求解【例1】在RtA ABC中，CB=3, C4=4, M为斜边AB ±一动点.过点M作MD丄AC于点D,过M 作ME丄CB于点E,则线段DE的最小值为__________________ .（四川省竞赛试题）解题思路：四边形CDMF为矩形，连结CM,则DE= CM,将问题转化为求CM的最小值.【例2】如图，在矩形ABCD中，4B=20cm, BC=10cm.若在AC, AB上各取一点M, N,使BM+M/V 的值最小，求这个最小值.（北京市竞赛试题）解题思路：作点8关于&C的对称点连结B'M, B'A,贝'J BM= B'M,从而BM+MN= B'M+MN.要使BM+MN的值最小，只需使FM十M/V的值最小，当B', M, N三点共线且B7V丄AB时，B'M+MN的值最小.【例3】如图，己知DABCD, AB=a, BC=b（a>b）, P为边上的一动点，直线DP交CB的延长线于Q.求AP+BQ的最小值. （永州市竞赛试题）解题思路：设AP=x,把AP, BQ分别用x的代数式表示，运用不等式以a2+b2>2ab或a+b》2范 (当且仅当a=b时取等号)来求最小值.【例4］阅读下列材料：问题如图1, 一圆柱的底面半径为5dm,高为5dm, BC是底面直径，求一只蚂蚁从A点出发沿圆柱表面爬行到C点的最短路线.小明设计了两条路线：沿AB剪开路线1：侧面展开图中的线段AC.如图2所示.设路线I的长度为/i，则/i2=AC2=AB2 +BC2 =25+(571)2=25+25n2.路线2：高线AB十底面直径BC.如图1所示.设路线 / 的长度为b，则 F = (BCMB)2=(5+10)2 =225.••/I2-/22 = 25+257T2-225=257r2-200=25(7T2-8), /. 42 >/22 , /. h>l2 .所以，应选择路线2.(1)小明对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为1分米，高AB为5分米"继续按前面的路线进行计算.请你帮小明完成下面的计算：路线1：h2=AC2= ____________ :路线2： /22= (AB+BC) 2= __________ .•••/『______ 於，・・・h___ /2(填“〉"或“<"),所以应选择路线__________ (填“1"或"2")较短.(2)请你帮小明继续研究：在一般情况下，当圆柱的底面半径为门高为h时，应如何选择上面的两条路线才能使蚂蚁从点&出发沿圆柱表面爬行到C点的路线最短. (衢州市中考试题)解题思路：本题考查平面展开一最短路径问题•比较两个数的大小，有时比较两个数的平方比较简便.比较两个数的平方，通常让这两个数的平方相减.【例5】如图，己知边长为4的正方形钢板，有一个角锈蚀，其中AF=2, BF=1.为了合理利用这块钢板，将在五边形EABCD内截取一个矩形块MD/VP,使点P在AB上，且要求面积最大，求钢板的最大利用率. (中学生数学智能通讯赛试题)解题思路：设DN* PN=y,则S=xy.建立矩形MD/VP的面积S与x的函数关系式，利用二次函数性质求S的最大值，进而求钢板的最大利用率.【例6】如图，在四边形ABCD 中,AD=DC=1, Z DAB=A DCB=90°, BC, AD 的延长线交于P,求AB& PAB 的最小值.（中学生数学智能通讯赛试题）AR PA解题思路：设PD=x （x>l ）,根据勾股定理求出PC,证RtA PCD- RtA PAB,得到 ——=——，求出 P AB,根据三角形的面积公式求出y=AB^P AB .整理后得到y$4,即可求出答案.能力训练A 级1. 如图，将两张长为8、宽为2的矩形纸条交叉，使重叠部分是一个菱形.容易知道当两张纸条 垂直时，菱形的周长有最小值，那么菱形周长的最大值是 ________________ .（烟台市中考试题）2. D 是半径为5cm 的O0内一点，且OD=3cm,则过点0的所有弦中，最短的弦 _______________ cm.（广州市中考试题）3. 如图，有一个长方体，它的长BC=4,宽AB=3,高BBi=5. —*只小虫由A 处出发，沿长方体表面 爬行到G ，这时小虫爬行的最短路径的长度是 ___________ .（"希望杯"邀请赛试题）4.如图，Uh ABC 中，AB=1Q, BC=6,经过点C 且与边AB 相切的动圆与CB, CA 分别相交于点E, F,则线段EF 长度的最小值是（）（兰州市中考试题）5. 如图，圆锥的母线长04=6,底面圆的半径为2. —小虫在圆锥底面的点&处绕圆锥侧面一周又第1题图A. 4A /2B. 4.75C. 5D. 4.8第4題图回到点则小虫所走的最短距离为（）（河北省竞赛试题）A. 12B. 4TIC. 6 VID. 6 羽6. 如图，已知Z MON= 40°, P 是Z MO N 内的一定点，点A, B 分别在射线OM, OA/上移动，当△网3 周长最小时，ZAPB 的值为（）（武汉市竞赛试题）A. 80°B. 100°C. 120°D. 140°7. 如图，血是以等边三角形ABC-边AB 为半径的四分之一圆周，P 为AD 上任意一点.若4C=5, 则四边形ACBP 周长的最大值是（）（福州市中考试题）A. 15B. 20C. 15+5V2D. 15+5 石交AB 于M,交DC 与N.⑴设AE=x,四边形ADNM 的面积为S,写出S 关于x 的函数关系式. （2）当AE 为何值时，四边形ADNM 的面积最大？最大值是多少？（山东省中考试题）9. 如图，六边形ABCDEF 内接于半径为/•的O0,其中AD 为直径，且AB=CD=DE=FA.（1）当Z BAD=75°时，求处的长； （2）求证：BCII 40II FE ：⑶设AB=X t 求六边形ABCDEF 的周长/关于x 的函数关系式，并指出x 为何值时，/取得最大值.10. 如图，已知矩形ABCD 的边长AB=2, BC=3,点P 是AD 边上的一动点（P 异于A 、D ）. Q 是BC第6题图&如图，在正方形ABCD 中，AB=2,第8題图E 是AD 边上一点（点E 与点A, D 不重合），BE 的垂直平分线第7題图边上任意一点.连结AQ ，DQ,过P 作PEII DQ 交于AQ 于F,作PF//AQ 交DQ 于F.（1） 求证：△&PE-厶 ADQ ；（2） 设&P 的长为X,试求APEF 的面积关于x 的函数关系式，并求当P 在何处时，取得 最大值？最大值为多少？（3）当Q 在何处时，AADQ 的周长最小？（须给出确定Q 在何处的过程或方法，不必证明）（无锡市中考试题）11. 在等腰AABC 中，AB=AC=5, BC=6.动点M, N 分别在两腰AB, AC 上（M 不与B 重合，N 不与A, C 重合），且M/VII BC.将NAMN 沿M/V 所在的直线折叠，使点A 的对应点为P.（1） 当MN 为何值时，点P 恰好落在BC 上？（2）设MN=x, △ MNP 与等腰NABC 重叠部分的面积为y,试写出y 与x 的函数关系式，当x 为何值时，y 的值最大，最大值是多少？（宁夏省中考试题）B 级1. 己知凸四边形ABCD 中，AB+AC+CD= 16,且S 馳彤MCO =32,那么当AC= _____________________ , BD= 时，四边形4BCD 面积最大，最大值是 _________ .（“华杯赛"试题）2. 如图，已知ZkABC 的内切圆半径为门Z4=60°, BC=2y[3 ,则/■的取值范围是 ___________ •（江苏 省竞赛试题）3. 如图O0的半径为2, O0内的一点P 到圆心的距离为1,过点P 的弦与劣弧金组成一个弓形,则此弓形面积的最小值为 __________4. 如图，A4BC 的面积为 1,点 D, G, E 和 F 分别在边 AB, AC, BC 上，BD<DA, DGII BC, DEWAC,A B第2题图 第3题图第4题图GFIIAB,则梯形DEFG面积的最大可能值为.（上海市竞赛试题）5.已知边长为a的正三角形ABC,两顶点A, B分别在平面直角坐标系的x轴，y轴的正半轴上滑动，点C在第一象限，连结0C,则0C的最大值是____________ •（潍坊市中考试题）6.已知直角梯形ABCD中，ADW BC,丄BC, AD=2, BC=DC=5,点P在BC上移动，则当必+ PD取最小值时，"PD中边AP上的高为（）（鄂州市中考试题）D. 3第6題图第7题图第8题图7.如图，正方形&BCD的边长为4cm,点P是BC边上不与点B, C重合的任意一点，连结AP,过点P 作PQ丄&P交DC于点Q.设BP的长为xcm, CQ的长为ycm.（1）求点P在BC上运动的过程中y的最大值；（2）当尸丄cm时，求x的值. （河南省中考试题）4&如图，y轴正半轴上有两点A（0, a）, 8（0, b）,其中a>b>0.在x轴上取一点C,使乙ACB最大, 求C点坐标. （河北省竞赛试题）9.如图，正方形&BCD的边长为1,点M, /V分别在BC, CD上，使得△ CMN的周长为2.求:（1）Z MAN的大小；（2）△MAN的面积的最小值. （“宇振杯"上海市竞赛试题）10,如图，四边形ABCD中，AD= CD, Z DAB=A ACB=90°,过点D作DE丄AC于F, DE与相交于GFIIAB,则梯形DEFG 面积的最大可能值为 .（上海市竞赛试题）点E.(1) 求证：AB AF=CB ・CD ；(2) 已知AB=15cm, 8C=9cm, P 是射线DE 上的动点，设DP=xcm(x>0),四边形BCDP 的面积为ycm 2. ① 求y 关于x 的函数关系式；② 当x 为何值时，NPBC 的周长最小？求出此时y 的值.(南通市中考试题)11. 如图，己知直线/： y = Rx+2 — 4R 伙为实数).(1) 求证：不论k 为任何实数，直线/都过定点M,并求点M 的坐标；(2) 若直线/与x 轴、y 轴的正半轴交于A, B 两点,求AAOB 面积的最小值.(太原市竞赛试题)12. 如图，在RtA ABC 中，Z C=90°, BC=2, AC=x,点F 在边AB ±,点G, H 在边BC 上，四边形 EFGH 是一个边长为y 的正方形，且AE=AC.(1) 求y 关于x 的函数解析式；(2) 当x 为何值时，y 取得最大值？求出y 的最人值.(上海市竞赛试题)第6题图第9题图专题25 平面几何的最值问题12~5提示：当CM丄AB时，CM值最小，CM =警詈例2如图.蜩+ M/V的最小值为点厅到离B'F, BE= ABBC = 4^5 cm, BB' = 8>/5 cm , AE = ACJ AB'_ BE'= 8>/5cm.在△ABF中，由丄BB，2AB的距•处=丄AB'B'F,得B'F=16cm.故BM + MN的最小值为216旳例3由5DS△呻得話喘’即话畔:.AP+BQ=x+--b. \'x+ — >2jx— = 2y/ab,・••当且仅当x x V x= 俪时，上式等号成立.故当AP=y^b时.AP+BQ最小，其最小值为2他（例5题图）-b.例4⑴£=25 + *, /； =49, /i</2,故要选择路线/较短.（2）/；=//+（〃）'，f =（方+ 2r）‘，一g=r[（沪一4”一4/?].当r=斗时，/f = 1},当r> 严厶时,I； > I；,当r<-^—时，/； < 7；. 例 5 设DN=x, PN=y,贝！）S=xy.由厶APQc^^ABF,得=丄_兀__4 _2-（4-x） 2即x=10—2y,代入S=xy 得S=xy=y（10—2y）,即S=-2（y-# 25 5+ —.因3<y<4,而）/=空不在自变量y的取值范围内，所以y=仝不是极值点.当y=3时.S（3）=12.当y=4时，S（4）=&故Smax=12.此2时，钢板的最大利用率——j ---------- =80%. 例6设PD=x（x〉l）,则PC= ,由RtAPCDcoA42— x2xl2咙得妇警.眉，令FS.则尸敎5如=斜’求y的最小值有时’y有最小值4.②运用基本不等式"弓+占S23222 r-1 2口+心•••当〒=口即当口时宀有最小值丄③借用判别式.去分母’得塔+2 (1—y) x+l+2y=0,由A=4 (1—y) 2—4 (l+2y) =4y (y —4) >0,得y>4, .'.y 的最小值为 4. A 级1. 17提示：当两张纸条的对角重合时，菱形周长最大.2.83. >/744.D5.D6. B7. C 提示：当点P 与点D 重合时.四边形ACBP 的周长最大.& ⑴连结 ME,过N 作 NF 丄ABTF.可证明 R^EBA^Rt^MNF,得 MF=AE=x.\'ME 2=AE 2+AM 2, 故 .即(2-AM) —X+AM, AM=1 一丄x 2,.・.S=人“十xAD=人“十力尸 x2422=AM+AM+MF=2AM+AE=2 (1 一丄F) +/= — 丄x 2+x+2.42(2) S=~- (x 2-2x+l) +-= 一丄(x-1)计？.故当胚=x=l 时，四边形ADNM 的面积最大,2 2 2 2 此时最大值为-.29. (1) BC 长为迥.(2)提示：连结BD (3)过点B 作BM 丄AD T M ・由 ⑵ 知四边形ABCD3AB ， x 2,W为等腰梯形.从而 BC=AD-2 AM=2r-2AM.由厶BAM^^DAB,得 AM=・・・BC=2/•—一.AD 2rr最大值6 r.10. (1) Z.APE= Z.ADQ, Z.AEP=Z.AQD.・'.^APE^^ADQ. (2)由厶APE^>^ADQ, 'PDFs'1 1 13 3 3ADQ, S\PEF = — SmPfQf,得 S APEF = — — x~~^~x =—— (x — — )，+—.故当 x=—时，即 P 是 AD 的中点2 3 3 2 4 2 时，Sw 取得最大值.(3)作A 关干直线BC 的对称点A f.连结D 川交BC 干Q,则这个Q 点就是使 △AD0周长最小的点，此时0是BC 的中点.11. (1)点P 恰好在BC 上时，由对称性知MN 是厶4肚 的中位线・・••当MN=^BC=3时，点P 在r"r"x同理.EF=2r- — .l=4x+2 (2 r-—)=--r r r(x-r) 2+6r (0<v<V2 r)..当 x=r^, l 取得(第8題图)5. 卑丄4提示：当04=03时.0C 的长最大.6.CBC 上.( 2）由已知得"BC 底边上的高力=J5L32 =4.①当0＜疋3时.如图1,连结AP 并延长交BC 干点D, AD 与MN 交干点0.2 12 1 1由MAWC,得A 。

数学初中竞赛函数最值专题训练一．选择题1．当三个非负实数x、y、z满足关系式x+3y+2z＝3与3x+3y+z＝4时，M＝3x﹣2y+4z的最小值和最大值分别是（）A．B．C．D．2．正实数a，b，c，d满足a+b+c+d＝1，设p＝+++，则（）A．p＞5 B．p＝5C．p＜5 D．p与5的大小关系不确定3．已知y＝+（x，y均为实数），则y的最大值与最小值的差为（）A．2﹣1 B．4﹣2C．3﹣2D．2﹣2 4．设x≥0，y≥0，2x+y＝6，则u＝4x2+3xy+y2﹣6x﹣3y的最小值是（）A．B．18 C．20 D．不存在5．代数式的最小值是（）A．0 B．C．D．6．设x是实数，y＝|x﹣1|+|x+1|．下列四个结论：Ⅰ．y没有最小值；Ⅱ．只有一个x使y取到最小值；Ⅲ．有有限多个x（不止一个）使y取到最大值；Ⅳ．有无穷多个x使y取到最小值．其中正确的是（）A．ⅠB．ⅡC．ⅢD．Ⅳ7．方程|x﹣1|+|y﹣1|＝1确定的曲线所围成的图形面积为（）A．4 B．3 C．2 D．18．如果a，b，c是正实数且满足abc＝1，则代数式（a+1）（b+1）（c+1）的最小值是（）A．64 B．8C．8 D．二．填空题9．代数式的最小值为．10．a，b是正数，并且抛物线y＝x2+ax+2b和y＝x2+2bx+a都与x轴有公共点，则a2+b2的最小值是．11．当|x|≤4时，函数y＝|x﹣1|+|x﹣2|+|x﹣3|的最大值减去最小值的差是：．12．若a，c，d都是整数，b是正整数，且a+b＝c，b+c＝d，c+d＝a，则a+b+c+d的最大值是．13．函数f（x）＝λx2+（λ﹣3）x+1对于任意实数x都有f（x）≤f（λ），则函数f（x）的最大值是．14．代数式的最小值是．15．函数y＝|x﹣1|+|x﹣2|+…+|x﹣10|，当x在实数范围内取值时，y的最小值是．16．a、b、c是非负实数，并且满足3a+2b+c＝5，2a+b﹣3c＝1．设m＝3a+b﹣7c，记x为m的最小值，y为m的最大值．则xy＝．三．解答题17．当﹣1≤x≤2时，函数y＝2x2﹣4ax+a2+2a+2有最小值2．求a所有可能取的值．18．已知非负实数x，y，z满足，记W＝3x+4y+5z．求W的最大值与最小值．19．附加题：某城镇沿环形路有五所小学，依次为一小、二小、三小、四小、五小，它们分别有电脑15，7，11，3，14台，现在为使各校电脑台数相等，各调几台给邻校：一小给二小，二小给三小，三小给四小，四小给五小，五小给一小．若甲小给乙小﹣3台，则乙小给甲小3台，要使电脑移动的总台数最小，应做怎样安排？20．阅读材料：若a，b都是非负实数，则a+b≥．当且仅当a＝b时，“＝”成立．证明：∵（）2≥0，∴a﹣+b≥0．∴a+b≥．当且仅当a＝b时，“＝”成立．举例应用：已知x＞0，求函数y＝2x+的最小值．解：y＝2x+≥＝4．当且仅当2x＝，即x＝1时，“＝”成立．当x＝1时，函数取得最小值，y最小＝4．问题解决：汽车的经济时速是指汽车最省油的行驶速度．某种汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油（+）升．若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．（1）求y关于x的函数关系式（写出自变量x的取值范围）；（2）求该汽车的经济时速及经济时速的百公里耗油量（结果保留小数点后一位）．21．设x1、x2、x3、x4、x5均为正整数，且x1+x2+x3+x4+x5≤x1x2x3x4x5．试求x5的最大值．22．某环形道路上顺时针排列着4所中学：A1，A2，A3，A4，它们顺次有彩电15台，8台，5台，12台．为使各校的彩电数相同，允许一些中学向相邻中学调出彩电．问怎样调配才能使调出的彩电台数最小？并求调出彩电的最小总台数．23．已知：实数x，y，z满足：x+y+z＝0，xy+yz+zx＝﹣3，求z的最大值．参考答案一．选择题1．解：由得：，代入M的表达式中得，M＝3x﹣2y+4z＝3x﹣（1﹣x）+4（2x﹣1）＝﹣，又因x、y、z均为非负实数，所以，即≤x≤1，当x＝时，M有最小值为﹣，当x＝1时，M有最大值为7．故选：B．2．解：∵a，b，c，d均为正数，且a+b+c+d＝1，∴必有0＜a，b，c，d＜1∵p＝+++，事实上我们在xOy坐标系中作出函数f（x）＝的图象，显然可以发现其图象一定在点（0，1）和（1，2）这两点连线的上方，而这两点连线的方程为y＝x+1，∴可以发现在（0，1）上恒有＞x+1，当然这样只是画图所得，未必准确，∴还要严格证明，证之如下：上式两边平方得：3x+1＞x2+2x+1，∴x2﹣x≤x（x﹣1）＜0，而此时x∈（0，1），可见上式显然成立．所以我们有：＞a+1，＞b+1，＞c+1，＞d+1，以上四式相加得p＝+++＞a+b+c+d+4＝5，即有P＞5．故选：A．3．解：∵y＝+，∴y2＝4+2＝4+2×，∵1≤x≤5，当x＝3时，y的最大值为2，当x＝1或5时，y的最小值为2，故当x＝1或5时，y取得最小值2，当x取1与5中间值3时，y取得最大值2，故y的最大值与最小值的差为2﹣2，故选：D．4．解：由已知得：y＝6﹣2x，代入u＝4x2+3xy+y2﹣6x﹣3y，整理得：u＝2x2﹣6x+18，而x≥0，y＝6﹣2x≥0，则0≤x≤3，u＝2（x﹣）2+，当x＝0或x＝3时，u取得最大值，u max＝18，当x＝时，u取得最小值，u min＝．故选：A．5．解：由题意得：，解得x≥0，又∵、、都是随x的增大而增大，∴当x＝0时，代数式取得最小值，此时式（）min＝+＝1+．故选：B．6．解：从数轴上可知，区间[﹣1，1]上的任一点x到点1与点﹣1的距离之和均为2；区间[﹣1，1]之外的点x到点1与点﹣1的距离之和均大于2．所以函数y＝|x﹣1|+|x+1|当﹣1≤x≤1时，取得最小值2．Ⅰ、y在区间[﹣1，1]上取得最小值2；故本选项错误；Ⅱ、y在区间[﹣1，1]上的任一点x到点1与点﹣1的距离之和均为2；故本选项错误；Ⅲ、y在区间[﹣1，1]之外的点x到点1与点﹣1的距离之和均大于2，且无限大，所以y在区间[﹣1，1]之外的点没有最大值；故本选项错误；Ⅳ、y在区间[﹣1，1]上的任一点x到点1与点﹣1的距离之和均为最小值2，所以有无穷多个x使y取到最小值．故本选项正确；故选：D．7．解：先考虑简单的情况：当|x|+|y|＝1时：当x＞0，y＞0时，x+y＝1，当x＞0，y＜0时，x﹣y＝1，当x＜0，y＞0时，y﹣x＝1，当x＜0，y＜0时，x+y＝﹣1，∴四条直线与坐标轴的交点分别为（0，1），（1，0），（﹣1，0），（0，﹣1），∴正方形边长为：＝，∴正方形面积为：×＝2．∵|x﹣1|+|y﹣1|＝1的在坐标系内的图象只不过是将|x|+|y|＝1的图象向右又向上移动了一个单位，图象的形状并未改变，∴其面积依然为2．故选：C．8．解：要使（a+1）（b+1）（c+1）取得最小值，则三个因式都应取得最小值，∵m+n≥2，当且仅当m＝n时取得最小值，故可得①当a＝1时，a+1取得最小值2；②当b＝1时，b+1取得最小值2；③当c＝1时，c+1取得最小值2；又∵a＝1，b＝1，c＝1可能满足条件abc＝1，∴代数式（a+1）（b+1）（c+1）的最小值＝2×2×2＝8．故选：C．二．填空题（共8小题）9．解：求代数式，即+的最小值，实际上就是求x轴上一点到（0，﹣2）以及（12，3）两点的和的最小值，而两点间的距离是线段最短，所以，点到（0，﹣2）到点（12，3）的距离即为所求，即＝13．故答案为：13．10．解：由题设知a2﹣8b≥0，4b2﹣4a≥0．则a4≥64b2≥64a，∵a，b是正数，∴a3≥64，∴a≥4，b2≥a≥4．∴a2+b2≥20．又∵当a＝4，b＝2时，抛物线y＝x2+ax+2b和y＝x2+2bx+a都与x 轴有公共点，∴a2+b2的最小值是20．故答案为：20．11．解：∵|x|≤4，∴，∴当x＝﹣4时，y取最大值18，当x＝2时，y取最小值2．则最大值与最小值的差是18﹣2＝16．故答案为：16．12．解：∵a+b＝c，①b+c＝d，②c+d＝a，③由①+③，得（a+b）+（c+d）＝a+c，∴b+d＝0，④b+c＝d；⑤由④+⑤，得∴2b+c＝b+d＝0，∴c＝﹣2b；⑥由①⑥，得∴a＝c﹣b＝﹣3b，⑦由④⑥⑦，得∴a+b+c+d＝（a+c）+（b+d）＝a+c＝﹣5b；∵b是正整数，∴b≥1，∴a+b+c+d≤﹣5，∴a+b+c+d的最大值是﹣5．故答案为：﹣5．13．解：由题意得，f（x）有最大值，则可得λ＜0，又∵f（x）＝λ（x+）2+1﹣，∴f（x）的最大值为1﹣，又∵f（x）≤f（λ），∴f（λ）＝λ3+（λ﹣3）λ+1＝1﹣，解得：λ＝1（舍去）或λ＝﹣，将λ＝﹣，代入可得f（x）的最大值为．故答案为：．14．解：若代数式有意义，则，解得：x≥2，∵，，是增函数，∴当x＝2时，代数式的值最小，即＝2+1+0＝3．故答案为3．15．解：设y1＝|x﹣1|+|x﹣10|，则y1可以看作数轴上点x到点1与10的距离和，即可得当x＝＝5.5时，y1取最小值，同理：设y2＝|x﹣2|+|x﹣9|，y3＝|x﹣3|+|x﹣8|，y4＝|x﹣4|+|x﹣7|，y5＝|x﹣5|+|x﹣6|，∴当x＝5.5时，y2，y3，y4，y5取最小值，∴当x＝5.5时，函数y＝|x﹣1|+|x﹣2|+…+|x﹣10|取最小值，最小值为：y＝|5.5﹣1|+|5.5﹣2|+…+|5.5﹣10|＝4.5+3.5+2.5+1.5+…+0.5+0.5+1.5+2.5+3.5+4.5＝25．故答案为：25．16．解：由3a+2b+c＝5，2a+b﹣3c＝1得⇒，∴可得a＝7c﹣3，b＝7﹣11c，由a、b、c是非负数得：⇒≤c≤，又m＝3a+b﹣7c＝3c﹣2，故﹣≤m≤﹣，于是可得x＝﹣，y＝﹣，故xy＝﹣×（﹣）＝．三．解答题（共7小题）17．解：y＝2x2﹣4ax+a2+2a+2图象的对称轴为：x＝a，①当﹣1≤a≤2时，函数在x＝a处取得最小值2，故﹣a2+2a+2＝2，即a2﹣2a＝0，解得：a＝0或2，②当a＜﹣1时，函数在x＝﹣1处取得最小值2，代入函数式得2+4a+a2+2a+2＝2，即：a2﹣6a+2＝0，解得：a＝﹣3±，取a＝﹣3﹣，③当a＞2时，函数在x＝2处取得最小值2，代入函数式得：8﹣8a+a2+2a+2＝2，即a2﹣6a+8＝0，解得：a＝2或4，取a＝4．故a所有可能的值为：﹣3﹣，0，2，4．18．解：设＝k，则x＝2k+1，y＝﹣3k+2，z＝4k+3，∵x，y，z均为非负实数，∴，解得﹣≤k≤，于是W＝3x+4y+5z＝3（2k+1）﹣4（3k﹣2）+5（4k+3）＝14k+26，∴﹣×14+26≤14k+26≤×14+26，即19≤W≤．∴W的最大值是35，最小值是19．19．解：如图，用A、B、C、D、E分别表示这五所小学的位置，并设A向B调x1台电脑，B向C调x2台电脑，…，E向A调x5台电脑，依题意有：7+x1﹣x2＝11+x2﹣x3＝3+x3﹣x4＝14+x4﹣x5＝15+x5﹣x1＝50÷5＝10，所以，x2＝x1﹣3，x3＝x1﹣2，x4＝x1﹣9，x5＝x1﹣5，设调动的电脑的总台数为y，则y＝|x1|+|x1﹣3|+|x1﹣2|+|x1﹣9|+|x1﹣5|，这样，这个实际问题就转化为求y的最小值问题，并由上面所得结论知：当x1＝＝3时，y的最小值为|3|+|3﹣3|+|3﹣2|+|3﹣9|+|3﹣5|＝12，即调动的总台数为12．因为x1＝3时，x2＝0，x3＝1，x4＝﹣6，x5＝﹣2，故一小就向二小调3台电脑，二小不调出，三小向四小调一台电脑，五小向四小调6台电脑，一小向五小调2台电脑．20．解：（1）∵汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油（+）升．∴y＝x×（+）＝（70≤x≤110）；（2）根据材料得：当时有最小值，解得：x＝90∴该汽车的经济时速为90千米/小时；当x＝90时百公里耗油量为100×（+）≈11.1升．21．解：由于x1、x2、x3、x4、x5在式中对称，故不妨设x1≤x2≤x3≤x4≤x5，并令S＝x1+x2+x3+x4+x5≤x1x2x3x4x5．则S≤5x5，即t＝x1x2x3x4≤5；那么t为1或2或3或4或5，而a，b，c，d则为t的约数．①当t＝5时，由于t＝1×5，故令x1＝x2＝x3＝1，x4＝5，代入S 可得x5＝2，与x4≤x5相矛盾，故x5＝2不合题意；②同理，当t＝1或4时均不合题意．当t＝3时，x5＝3，符合题意；③当t＝2时，由于t＝1×2，令x1＝x2＝x3＝1，x4＝2，代入S可得x5＝5，符合题意；综上所述，故x5的最大值为5．22．解：设A1中学调给A2彩电x1台（若x1＜0，则认为是A2，向A1调出|x1|台），A2中学调给A3彩电x2台，A3调给A4x3台，A4调给A1x4台．∵共有40台彩电，平均每校10台，∴15﹣x1+x4＝10，8﹣x2+x1＝10，5﹣x3+x2＝10，12﹣x4+x3＝10，∴x4＝x1﹣5，x1＝x2+2，x2＝x3+5，x3＝x4﹣2，x3＝（x1﹣5）﹣2＝x1﹣7，x2＝（x1﹣7）+5＝x1﹣2．本题即求y＝|x1|+|x2|+|x3|+|x4|＝|x1|+|x1﹣2|+|x1﹣7|+|x1﹣5|的最小值，其中x1是满足﹣8≤x1≤15的整数．设x1＝x，并考虑定义在﹣8≤x≤15上的函数：y＝|x|+|x﹣2|+|x ﹣7|+|x﹣5|，当2≤x≤5时，y取最小值10，即当x1＝2，3，4，5时，|x1|+|x1﹣2|+|x1﹣7|+|x1﹣5|取到最小值10．从而调出彩电的最小台数为10，调配方案有如下4种：23．解：∵x+y+z＝0，∴x+y＝﹣z，①∵xy+yz+zx＝﹣3，∴xy＝﹣3﹣（yz+zx）＝﹣3﹣z（x+y）＝﹣3﹣z（﹣z），即xy＝﹣3+z2，②由①②及韦达定理知：xy是一元二次方程w2+zw+（﹣3+z2）＝0的两实根，则判别式△＝z2﹣4（﹣3+z2）≥0，化简得：z2≤4，∴﹣2≤z≤2，∴z的最大值是2．。

初三代数竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是方程2x - 3 = 7的解？A. x = 2B. x = 5C. x = 10D. x = 8答案：B2. 如果一个数的平方等于它的4倍，那么这个数是多少？A. 0 或 4B. 0 或 2C. 0 或 -4D. 0 或 -2答案：B3. 计算下列表达式的值：(3x - 2)(x + 1) - 5xA. 2x + 1B. 4x - 2C. 3x - 2D. 5x + 1答案：A4. 一个数的3倍加上另一个数的2倍等于20，如果第一个数是4，那么第二个数是多少？A. 2B. 4C. 6D. 8答案：A5. 一个两位数，其个位数字是十位数字的两倍，且这个数小于50，这个数是多少？A. 22B. 33C. 44D. 21答案：A6. 一个数的立方等于它本身，这个数可以是哪些？A. 0, 1, -1B. 0, 2, -2C. 0, 1, 2D. 0, 1, -1, 2答案：A7. 一个数的相反数是它本身的一半，这个数是多少？A. 0B. 2C. -2D. 1答案：C8. 一个数的绝对值是它本身的两倍，这个数是多少？A. 0B. 2C. -2D. 1答案：A9. 计算下列表达式的值：(2x + 3)(2x - 3)A. 4x^2 - 9B. 4x^2 + 9C. 9 - 4x^2D. -9 + 4x^2答案：A10. 如果一个数的一半加上3等于它本身，那么这个数是多少？A. 6B. -6C. 3D. -3答案：A二、填空题（每题4分，共20分）1. 一个数的平方等于36，这个数是______。

答案：±62. 如果一个数的立方等于-27，那么这个数是______。

答案：-33. 一个数的倒数是它本身的两倍，这个数是______。

答案：1/3 或 -1/34. 如果一个数的绝对值是它本身的三倍，那么这个数是______。

答案：05. 一个两位数，其个位数字是十位数字的三倍，这个数是______。

29.最值问题知识纵横求某个量、或者几个量的和、差、积、商的最大值和最小值，是数学问题中的一种常见类型，又在实际生活与生产实践中，我们经常碰到一些带有“最”字的问题,如投入最少、路程最短、材料最省等，这些问题我们称之为最值问题，•在现阶段，解这类问题的基本知识与基本方法有：1.穷举获取;2.运用非负数的性质;3.利用不等分析逼近求解;4.使用几何公理、定理、性质等.解这类问题时,既要说明最值可以达到,又要证明不可能比所求的值更大(•或更小),前者需构造一个恰当的例子,后者需要详细说理.例题求解【例1】设自然数x,y,m,n满足条件58x y my m n===,则x+y+m+n的最小值是_____.(湖北省黄冈市竞赛题) 思路点拨把连等式拆开用,用一个字母的代数式表示另一个字母,利用隐含整除条件,分别求出x,y,m,n的最小值.解:1157 提示:x=58y,m=85y,n=85m=6425y,因25│y,8│y,故y有最小值200.【例2】设a、b、c满足a2+b2+c2=9,那么代数式(a-b)2+(b-c)2+(c-a)2的最大值是( • ).A.27B.18C.15D.12 (全国初中数学联赛题)思路点拨利用乘法公式,把代数式变形成与已知条件关联的式子,进而求出最大值.解:选A 提示:原式=3(a2+b2+c2)-(a+b+c)2≤27【例3】已知n、k均为自然数,且满足不等式761311nn k<<+,若对于某一给定的自然数n,只有惟一的一个自然数k使不等式成立,求所有符合要求的自然数n中的最大数和最小数.(“希望杯”邀请赛试题) 思路点拨解关于k的不等式组,利用已知条件的约束,通过穷举求出n的最大数与最小数.解:提示:由761311nn k<<+,得111367n kn+<<5667kn<<, ①5667n nk<<②因k 为自然数,且对于给定的n 来说,k 的值只有一个. 故6576n n ≤2 ,得n ≤84 当n=84时,代入②有 70<k<72,惟一的k 值为71,又由①得 n>7当n=8,n=9,n=10,…,n=12时,有623<k<667,712<k<757,813<k<847,916<k<937,10<k<1027,• 没有符合条件的整数k当n=13时,有1056<k<1117,得k=11 综上知n 的最大值为84,n 的最小值为13.【例4】某人租用一辆汽车从A 城前往B 城,沿途可能经过的城市以及通过两城市之间所需的时间(单位:小时)如图所示,若汽车行驶的平均速度为80千米/时,而汽车每行驶1千米需要的平均费用为1.2元,试指出此人从A 城出发到B 城的最短路线,并求出所需费用最少为多少元? (2003年全国初中数学竞赛题)思路点拨 即要求出此人从A 城出发到B 城的最短时间,而从A 城到B•城有多条线路,故只需一一列举,比较就可得出结论.解:从A 城出发到B 城的路线有如下两类:(1)从A 城出发到达B 城,经过O 城,因从A 城到O 城所需最短时间为26小时,从O 城到B 城所需最短时间为22小时,故此类路线所需最短时间为26+22=48小时. (2)从A 城出发到达B 城,不经过O 城,这时从A 城到B 城,必定经过C 、D 、E 城或F 、G 、H 城,所需时间至少为49小时,综上,从A 城到达B 城所需的最短时间为48小时,所走的路线为A →F →O →E →B,所需的费用最少为80×48×1.2=4608(元)【例5】某家电生产企业根据市场调查分析,决定调整产品方案,•准备每周(•按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,•已知生产这些家问:(以千元为单位)? (2003年河南省竞赛题)思路点拨 设每周生产空调器、彩电、冰箱各x 台、y 台、z 台，产值为s ，可得关于x 、y 、z 的混合方程组，通过消元，建立一元不等式组，通过解不等式组，•确定相应字母取值范围，进而求出s 的最大值。

1.代数最值：23．（本小题7分）如图，平行四边形ABCD中，AD=8,CD=4,∠D=60°，点P与点Q是平行四边形ABCD边上的动点，点P以每秒1个单位长度的速度，从点C运动到点D，点Q以每秒2个单位长度的速度从点A→点B→点C运动．当其中一个点到达终点时，另一个点随之停止运动．点P与点Q同时出发，设运动时间为t，△CPQ的面积为S．（1）求S关于t的函数关系式；（2）求出S的最大值；（3）t为何值时，将△CPQ以它的一边为轴翻折，翻折前后的两个三角形所组成的四边形为菱形．2.几何最值：相似构造二次函数：24．如图，在平面直角坐标系中，是坐标原点，点A 、B 的坐标分别为和，连结．（1）现将绕点按逆时针方向旋转90°，得到，（点A 落到点C 处），请画出，并求经过、、三点的抛物线对应的函数关系式；（2）将（1）中抛物线向右平移两个单位，点的对应点为点，平移后的抛物线与原抛物线相交于点．为平移后的抛物线对称轴上一个动点，连结，当取得最大值时，求点P 的坐标；（3）在（2）的条件下，当点在抛物线对称轴上运动时，是否存在点使为直角三角形？如果存在，请求出点的坐标；如果不存在，请说明理由．周长最小：2５．已知抛物线经过点A （1，3）和点B （2，1）． （1）求此抛物线解析式；（2）点C 、D 分别是轴和轴上的动点，求四边形ABCD 周长的最小值； （3）过点B 作轴的垂线，垂足为E 点．点P 从抛物线的顶点出发，先沿抛物线的对称轴到达F 点,再沿FE 到达E 点，若P 点在对称轴上的运动速度是它在直线FE倍,试确定点F 的位置,使得点P 按照上述要求到达E 点所用的时间最短．（要求：简述确定F 点位置的方法，但不要求证明）O )3,0(A )0,5(B AB AOB △O COD ∆COD ∆B C D B E F P PF PE 、PF PE -P P EPF ∆P 21y ax bx =++x y x二．直线平分平行四边形面积24．如图，在平面直角坐标系中，A （0），B （2）.把矩形OABC 逆时针旋转30︒得到矩形111OA B C .（1）求1B 点的坐标；（2）求过点（2，0）且平分矩形111OA B C 面积的直线l 方程；（3）设（2）中直线l 交y 轴于点P ，直接写出1PC O ∆与11PB A ∆的面积和的值及1POA∆与11PBC ∆的面积差的值.三．交点问题23. 已知抛物线C 1：22y x x =-的图象如图所示，把C 1的图象沿y 轴翻折，得到抛物线C 2的图象，抛物线C 1与抛物线C 2的图象合称图象C 3． （1）求抛物线C 1的顶点A 坐标，并画出抛物线C 2（2）若直线y kx b =+与抛物线2(0)y ax bx c a =++≠且只有一个交点时,称直线与抛物线相切. 若直线y x b =+与抛物线C 1相切，求b 的值；（3）结合图象回答，当直线y x b =+与图象C 3 点时，b 的取值范围． 四．圆23．已知一元二次方程的一根为 2． （1）求关于的函数关系式；（2）求证：抛物线与轴有两个交点；（3）设抛物线与x 轴交于A 、B 两点（A 、B 不重合），且以AB 为直径的圆正好经过该抛物线的顶点．求的值．210x px q +++=q p 2 y x px q =++x 21y x px q =+++,p q五．规律25.已知：如图，在平面直角坐标系中，点0P 的坐标为(1，0)，将线段0OP 按逆时针方向旋转︒45，再将其长度伸长为0OP 的2倍，得到线段1OP ；又将线段1OP 按逆时针方向旋转︒45，长度伸长为1OP 的2倍，得到线段2OP ；如此下去，得到线段3OP ，4OP ，…，n OP （n 为正整数）（1）求点6P 的坐标； （2）求65OP P ∆的面积；（3）我们规定：把点n P （n x ，n y ）（ ,3,2,1,0=n ）的横坐标n x ，纵坐标n y ，都取绝对值后得到的新坐标（||n x ，||n y ），称之为n P 的“绝对坐标”。

初三数学奥赛代数最值问题
姓名：
求最值问题的方法归纳起来有如下几点：
1、运用配方法求最值
例1、实数x、y满足2- 6x+=0，则++2x的最大值是
例2、m=的最小值为（简单分式函数求最值的基本方法）练习：1、若实数x、y满足++3xy=35，则xy的最大值是
2、（1）求函数y=在3≦x≦5时的最值；
（2）求y=的最大值；
3、设、是关于x的一元二次方程+ax+a=2的两个实数根，则（- 2）（- 2）的最大值为
例3、求y=+的最大值和最小值；（与二次根式相关的最值问题）练习：已知y=+，那么y的最大值与最小值的差为；
2、构造一元二次方程，在方程有解的条件下，利用判别式求最值
例1、实数x、y、z满足x+y+z=5，xy+yz+zx=3，求z的最大值；
例2、设a、b为实数，求代数式+ab+-a-2b的最小值；
练习：1、已知实数a、b、c满足a+b+c=0，++=6, 则a的最大值是
2、已知实数a、b满足+ab+=1,且t=ab - -，则t的最大值是，最小值是
3、建立函数模型求最值（略）
4、利用基本不等式求最值
例、设x、y、z为正数，且xyz（x+y+z）=4，则（x+y）（y+z）的最小值为；
练习：函数y=-x- +18（x﹥0）的最大值为；
5、利用不等分析法求最值
例、已知x、y、z为三个非负实数，且满足3x+2y+z=5，x+y –z=2，若s=2x+y –z，则s的最大值与最小值的和为；
练习：1、已知a﹤3，b﹥3,且a+b=k -1，ab=3，则k的最小整数值为；
2、若、都满足条件︱2x-1︱+︱2x+3︱=4，且﹤，则-的取值范围
是。

年初三数学竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. 1C. 2D. -12. 一个长方体的长、宽、高分别是8cm、6cm和5cm，其体积是多少立方厘米？A. 240B. 180C. 120D. 1003. 一个数的60%加上它的40%等于这个数的：A. 100%B. 80%C. 60%D. 40%4. 下列哪个分数是最接近1的？A. 1/2B. 3/4C. 4/5D. 9/105. 一个数除以3的商是15，这个数是多少？A. 45B. 54C. 60D. 406. 一个正方形的面积是64平方厘米，它的周长是多少厘米？A. 32B. 48C. 64D. 167. 一个班级有21个男生和9个女生，男生人数占全班的百分比是多少？A. 70%B. 75%C. 80%D. 85%8. 一本书的价格是35元，如果打8折，那么现价是多少元？A. 28B. 30C. 35D. 429. 一个数的1/3加上它的1/4等于7/12，这个数是多少？A. 12B. 3C. 4D. 910. 一个长方体的长是15cm，宽是10cm，如果高增加5cm，体积将增加多少立方厘米？A. 750B. 500C. 375D. 250二、填空题（每题4分，共20分）11. 一个数的1/2与它的1/3的和是5/6，这个数是_________。

12. 一本书的原价是x元，打7折后售价为0.7x元，如果售价是21元，那么原价是_________元。

13. 一个长方形的长是14cm，宽是长的1/2，这个长方形的面积是_________平方厘米。

14. 一个数的3倍加上这个数的2倍等于36，这个数是_________。

15. 一个数的75%是45，那么这个数的50%是_________。

三、解答题（共两题，每题25分）16. 一个长方体的长、宽、高分别是12cm、10cm和8cm，求这个长方体的表面积和体积。

全国初中数学竞赛 试题参考答案及评分标准一、选择题（共5小题，每小题7分，满分35分） （1）设x =，则代数式(1)(2)(3)x x x x +++的值为( ). （A ）0 （B ）1 （C ）﹣1 （D ）2【答】C ．解：由已知得2310x x ++=， 于是2222(1)(2)(3)(3)(32)(31)1 1.x x x x x x x x x x +++=+++=++-=-（2）已知x y z ，，为实数，且满足253x y z +-=，25x y z --=-，则222x y z ++的最小值为( ).（A ）111（B ）0 （C ）5 （D ）5411【答】D ．解：由 25325x y z x y z +-=⎧⎨--=-⎩，， 可得 312.x z y z =-⎧⎨=+⎩，于是 22221125x y z z z ++=-+．因此，当111z =时，222x y z ++的最小值为5411． （3）若1x >，0y >，且满足3y y xxy x x y==，，则x y +的值为( ).（A ）1 （B ）2 （C ）92（D ）112【答】C ．解：由题设可知1y y x -=，于是 341y y x yx x -==，所以411y -=．故12y =，从而4=x ．于是92x y +=．（4）设333311111232011S =++++，则4S 的整数部分等于( ). （A ）4 （B ）5 （C ）6 （D ）7【答】A ．解：当2 3 2011k =，，，，因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦， 所以333111111511123201122201120124S ⎛⎫<=++++<+-< ⎪⨯⎝⎭． 于是有445S <<，故4S 的整数部分等于4．（5）点D E ，分别在△ABC 的边AB AC ，上，BE CD ，相交于点F ，设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形，，，，则13S S 与24S S 的大小关系为( ).（A ）1324S S S S < （B ）1324S S S S = （C ）1324S S S S > （D ）不能确定 【答】C ．解：如图，连接DE ，设1DEF S S ∆'=， 则1423S S EF S BF S '==，从而有1324S S S S '=．因为11S S '>，所以1324S SSS >．二、填空题（共5小题，每小题7分，共35分）（6）两条直角边长分别是整数a b ，（其中2011b <），斜边长是1b +的直角三角形的个数为 .【答】31．解：由勾股定理,得 12)1(222+=-+=b b b a ．因为b 是整数，2011<b ，所以2a 是1到4023之间的奇数，而且是完全平方数，这样的数共有31个，即2223 5 63，，，．因此a 一定是3，5，…，63，故满足条件的直角三角形的个数为31．（7）一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，2，3，3，4；另一枚质地均匀的正方体骰子的六个面上的数字分别是1，3，4，5，6，8. 同时掷这两枚骰子，则其朝上的面两数之和为7的概率是 .【答】16．解： 在36对可能出现的结果中，有6对：（1，6）， （2，5）， （2，5）， （3，4），（3，4），（4，3）的和为7，所以朝上的面两数字之和为7的概率是61366=.（8）若y =的最大值为a ，最小值为b ，则22a b +的值为 .【答】32．解：由1x -≥0，且12x -≥0，得12≤x ≤1．21122y =+=+ 由于13124<<，所以当34x =时，2y 取到最大值1，故1a =．当12x =或1时，2y 取到最小值12，故2b =．所以，2232a b +=．（9）如图，双曲线xy 2=（x ＞0）与矩形OABC 的边CB ， BA 分别交于点E ，F ，且AF=BF ，连接EF ，则△OEF 的面积为 .【答】32．解：如图，设点B 的坐标为a b （,）,则点F 的坐标为2ba （，）.因为点F 在双曲线2y x=上，所以 4.ab = 又点E 在双曲线上，且纵坐标为b ，所以点E 的坐标为2(,)b b.于是11212222221312.22OEF OEC FBEOFBC S S S S b b b a b a b b ab ∆∆∆=--=+-⨯⨯-⨯⨯-=+-=梯形（）（）（） （10）如图，在Rt △ABC 中，斜边AB 的长为35，正方形CDEF 内接于△ABC ，且其边长为12，则△ABC 的周长为 .【答】84．解：如图，设BC ＝a，AC ＝b ， 则22235a b +=＝1225． ① 又Rt △AFE ∽Rt △ACB ， 所以FE AF CB AC =，即1212b a b-=， 故12()a b ab +=． ②由①②得 2222122524a b a b ab a b +=++=++（）（），解得a ＋b ＝49（另一个解－25舍去），所以 493584a b c ++=+=．三、解答题（共4题，每题20分，共80分）（11）已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1，求a b c ++的值.解：设方程20x ax b ++=的两个根为αβ，，其中αβ，为整数，且α≤β，则方程20x cx a ++=的两根为11αβ++，，由题意得()()11a a αβαβ+=-++=，， ………………………………5分两式相加，得2210αβαβ+++=，即 (2)(2)3αβ++=， 所以，2123αβ+=⎧⎨+=⎩，；或232 1.αβ+=-⎧⎨+=-⎩，………………………………10分 解得 11αβ=-⎧⎨=⎩，； 或53.αβ=-⎧⎨=-⎩，又因为[11]a b c αβαβαβ=-+==-+++（），，（）（）， 所以012a b c ==-=-，，；或者8156a b c ===，，， 故3a b c ++=-，或29. ………………………………………………20分（12）如图，点H 为△ABC 的垂心，以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ，延长AD 交CH 于点P ，求证：点P 为CH 的中点.证明：如图，延长AP 交⊙2O 于点Q ， 连接 AH BD QB QC QH ，，，，.因为AB 为⊙1O 的直径，所以∠ADB =∠90=︒BDQ ．…………5分 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥，. ……………………………………………………10分又因为点H 为△ABC 的垂心，所以.AH BC BH AC ⊥⊥，所以AH ∥CQ ，AC ∥HQ ， 四边形ACQH为平行四边形. ………………………………………………15分所以点P 为CH 的中点. ………………………………………………20分（13） 如图，点A 为y 轴正半轴上一点，A B ，两点关于x 轴对称，过点A 任作直线交抛物线223y x =于P ，Q 两点. （Ⅰ）求证：∠ABP =∠ABQ ； （Ⅱ）若点A 的坐标为（0，1）， 且∠PBQ =60º，试求所有满足条件的 直线PQ 的函数解析式.解：（Ⅰ）如图，分别过点P Q ，　作y. 设点A 的坐标为（0，t ），则点B 的坐标为（0，-t ）. 设直线PQ 的函数解析式为y kx t =+,并设P Q ，的坐标分别为 P P x y （，）,Q Q x y （，）.由223y kx t y x =+⎧⎪⎨=⎪⎩，， 得2203x kx t --=，于是 32P Q x x t =-，即 23P Q t x x =-.于是，222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- …………5分又因为P Q x PC QD x =-，所以BC PCBD QD=. 因为∠BCP =∠90BDQ =︒，所以△BCP ∽△BDQ . 故∠ABP =∠ABQ . …………………………………………………………10分（Ⅱ）解法一 设PC a =，DQ b =，不妨设a ≥b >0， 由（Ⅰ）可知∠ABP =∠30ABQ =︒，BC，BD， 所以 AC2-，AD=2. 因为PC ∥DQ ，所以△ACP ∽△ADQ . 于是PC ACDQ AD=，即a b．所以a b +=． 由（Ⅰ）中32P Q x x t =-，即32ab -=-，所以322ab a b =+=，于是，可求得2==a b将2b =代入223y x =，得到点Q 的坐标，12）. …………………15分再将点Q 的坐标代入1y kx =+，求得=k .所以直线PQ 的函数解析式为13y x =-+. 根据对称性知，所求直线PQ 的函数解析式为1y =+，或1y x =+. ………………20分解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由（Ⅰ）可知，∠ABP =∠30ABQ =︒，所以2BQ DQ =.故 2Q x =将223Q Q y x =代入上式，平方并整理得 4241590Q Q x x -+=，即22(43)(3)0Q Q x x --=.所以 2Q x =. 又由（Ⅰ），得3322P Q x x t =-=-，32P Q x x k +=.若2Q x =代入上式得 P x = 从而 2()3P Q k x x =+=.同理，若Q x = 可得2P x =-从而 2()33P Q k x x =+=.所以，直线PQ 的函数解析式为1y x =+，或1y x =+. ………………………………………20分（14）已知0122011i a i >=，，　，　，　，且122011a a a <<<，证明：122011a a a ，，，中一定存在两个数i j a a i j <，（），使得(1)(1)2010i j j i a a a a ++-<．证明：令20101 2 20111i ix i a ==+，，，，， ……………………………………5分则20112010102010x x x <<<<<. …………………………………10分故一定存在1≤k ≤2010， 使得11k k x x +-<，从而120102010111k k a a +-<++． …………………………………15分即11(1)(1)2010k k k k a a a a ++++-<． …………………………………………20分。

中考数学最值问题总结考查知识点：1、“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。

（2、代数计算最值问题 3、二次函数中最值问题） 问题原型：饮马问题 造桥选址问题 （完全平方公式 配方求多项式取值 二次函数顶点） 出题背景变式：角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。

解题总思路：找点关于线的对称点实现“折”转“直” 几何基本模型： 条件：如下左图，A 、B 是直线l 同旁的两个定点． 问题：在直线l 上确定一点P ，使PA PB +的值最小． 方法：作点A 关于直线l 的对称点A '，连结A B '交l 于 点P ，则PA PB A B '+=的值最小例1、如图，四边形ABCD 是正方形，△ABE 是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM ．（1）求证：△AMB ≌△ENB ；（2）①当M 点在何处时，AM+CM 的值最小；②当M 点在何处时，AM+BM+CM 的值最小，并说明理由；（3）当AM+BM+CM 的最小值为 时，求正方形的边长。

AB A '′Pl例2、如图13，抛物线y=ax2＋bx＋c(a≠0)的顶点为（1,4），交x轴于A、B，交y轴于D，其中B点的坐标为（3,0）（1）求抛物线的解析式（2）如图14，过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，若直线PQ为抛物线的对称轴，点G为PQ上一动点，则x轴上是否存在一点H，使D、G、F、H四点围成的四边形周长最小.若存在，求出这个最小值及G、H的坐标；若不存在，请说明理由.（3）如图15，抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线M N∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD，若存在，求出点T的坐标；若不存在，说明理由.例3、如图1，四边形AEFG与ABCD都是正方形，它们的边长分别为a,b(b≥2a),且点F在AD上（以下问题的结果可用a,b表示）（1）求S△DBF;(2) 把正方形AEFG绕点A逆时针方向旋转450得图2,求图2中的S△DBF;(3) 把正方形AEFG绕点A旋转任意角度,在旋转过程中,S△DBF是否存在最大值,最小值?如果存在,试求出最大值、最小值；如果不存在，请说明理由。

专题33 最值问题在中学数学题中，最值题是常见题型，围绕最大（小）值所出的数学题是各种各样，就其解法，主要为以下几种：二次函数y ax bx c =++2（a 、b 、c 为常数且a ≠0）其性质中有①若a >0当x b a =-2时，y 有最小值。

y ac b a min =-442；②若a <0当x b a =-2时，y 有最大值。

y ac b amax =-442。

一次函数y kx b k =+≠()0的自变量x 的取值X 围是全体实数，图象是一条直线，因而没有最大（小）值；但当m x n ≤≤时，则一次函数的图象是一条线段，根据一次函数的增减性，就有最大（小）值。

3. 判别式法根据题意构造一个关于未知数x 的一元二次方程；再根据x 是实数，推得∆≥0，进而求出y 的取值X 围，并由此得出y 的最值。

“最值”问题中一般都存在某些变量变化的过程，因此它们的解往往离不开函数。

5. 利用非负数的性质在实数X 围内，显然有a b k k 22++≥，当且仅当a b ==0时，等号成立，即a b k 22++的最小值为k 。

6. 零点区间讨论法用“零点区间讨论法”消去函数y 中绝对值符号，然后求出y 在各个区间上的最大值，再加以比较，从中确定出整个定义域上的最大值。

7. 利用不等式与判别式求解在不等式x a ≤中，x a =是最大值，在不等式x b ≥中，x b =是最小值。

8. “夹逼法”求最值在解某些数学问题时，通过转化、变形和估计，将有关的量限制在某一数值X 围内，再通过解不等式专题知识回顾获取问题的答案，这一方法称为“夹逼法”。

【例题1】（经典题）二次函数y=2（x﹣3）2﹣4的最小值为．【答案】﹣4．【解析】题中所给的解析式为顶点式，可直接得到顶点坐标，从而得出解答．二次函数y=2（x﹣3）2﹣4的开口向上，顶点坐标为（3，﹣4），所以最小值为﹣4．【例题2】（2018某某）如图，AB是⊙O的弦，AB=5，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、AC的中点，则MN长的最大值是．【答案】．【解析】根据中位线定理得到MN的最大时，BC最大，当BC最大时是直径，从而求得直径后就可以求得最大值．如图，∵点M，N分别是AB，AC的中点，∴MN=BC，∴当BC取得最大值时，MN就取得最大值，当BC是直径时，BC最大，连接BO并延长交⊙O于点C′，连接AC′，∵BC′是⊙O的直径，专题典型题考法及解析∴∠BAC ′=90°． ∵∠ACB=45°，AB=5， ∴∠AC ′B=45°，∴BC ′===5，∴MN 最大=．【例题3】（2019某某某某）已知抛物线y ＝ax 2＋bx ＋c （a ≠0）过点A (1，0)，B (3，0)两点，与y 轴交于点C ，OC ＝3．（1）求抛物线的解析式及顶点D 的坐标；（2）过点A 作AM ⊥BC ，垂足为M ，求证：四边形ADBM 为正方形；（3）点P 为抛物线在直线BC 下方图形上的一动点，当△PBC 面积最大时，求P 点坐标及最大面积的值； （4）若点Q 为线段OC 上的一动点，问AQ ＋12QC 是否存在最小值?若存在，求岀这个最小值；若不存在，请说明理由．【思路分析】（1）将A 、B 、C 三点坐标代入抛物线的解析式即可求出a 、b 、c 的值（当然用两根式做更方便）；（2）先证四边形AMBD 为矩形，再证该矩形有一组邻边相等，即可证明该四边形为正方形；（3）如答图2，过点P 作PF ⊥AB 于点F ，交BC 于点E ，令P (m ，m 2－4m ＋3)，易知直线BC 的解析式为y ＝－x ＋3，则E (m ，－m ＋3)，PE ＝(－m ＋3)－(m 2－4m ＋3)＝－m 2＋3m ．再由S △PBC ＝S △PBE ＋S △CPE ，转化为12PE •OB ＝12×3×(－m 2＋3m )，最后将二次函数化为顶点式即可锁定S △PBC 的最大值与点P 坐标；（4）解决本问按两步走：一找（如答图3，设OQ ＝t ，则CQ ＝3－t ，AQ ＋12QC 1(3)2t -，取CQ 的中点G ，以点Q 为圆心，QG 的长为半径作⊙Q ，则当⊙Q 过点A 时，AQ ＋12QC ＝⊙Q 的直径最小）、二求（由 AQ ＝12QC ，解关于t 的方程即可）．【解题过程】（1）∵抛物线y ＝ax 2＋bx ＋c （a ≠0）过点A (1，0)，B (3，0)两点， ∴令抛物线解析为y ＝a (x －1)(x －3)． ∵该抛物线过点C (0，3)，∴3＝a ×(0－1)×(0－3)，解得a ＝1．∴抛物线的解析式为y ＝(x －1)(x －3)，即y ＝x 2－4x ＋3． ∵y ＝x 2－4x ＋3＝(x －2)2－1， ∴抛物线的顶点D 的坐标为(2，－1)．综上，所求抛物线的解析式为y ＝x 2－4x ＋3，顶点坐标为(2，－1)． （2）如答图1，连接AD 、BD ，易知DA ＝DB ． ∵OB ＝OC ，∠BOC ＝90°， ∴∠MBA ＝45°． ∵D (2，－1)，A (3，0)， ∴∠DBA ＝45°． ∴∠DBM ＝90°． 同理，∠DAM ＝90°． 又∵AM ⊥BC ，∴四边形ADBM 为矩形． 又∵DA ＝DB ，∴四边形ADBM 为正方形．（3）如答图2，过点P 作PF ⊥AB 于点F ，交BC 于点E ，令P (m ，m 2－4m ＋3)，易知直线BC 的解析式为y ＝－x ＋3，则E (m ，－m ＋3)，PE ＝(－m ＋3)－(m 2－4m ＋3)＝－m 2＋3m ．∵S △PBC ＝S △PBE ＋S △CPE ＝12PE •BF ＋12PE •OF ＝12PE •OB ＝12×3×(－m 2＋3m ) ＝－32 (m －32)2＋278，∴当m ＝32时，S △PBC 有最大值为278，此时P 点的坐标为(32，－34)．（4）如答图3，设OQ ＝t ，则CQ ＝3－t ，AQ ＋12QC 1(3)2t -， 取CQ 的中点G ，以点Q 为圆心，QG 的长为半径作⊙Q ，则当⊙Q 过点A 时，AQ ＋12QC ＝⊙Q 的直径最小，此时，√t 2+1=12(3−t )，解得t ＝2√63－1，于是AQ ＋12QC 的最小值为3－t ＝3－(2√63－1)＝4－2√63．专题典型训练题1.（2018某某）要使代数式√2−3t 有意义，则x 的（ ）2323 3232【答案】A.【解析】要使代数式√2−3t 有意义，必须使2-3x ≥0，即x ≤23，所以x 的最大值为23。

初中数学竞赛专题选讲(初三.20)最大 最小值一、内容提要1. 求二次函数y=ax 2+bx+c(a ≠0)，的最大、最小值常用两种方法：①配方法：原函数可化为y=a(x+ab 2)2+a b ac 442-.∵在实数范围内(x+ab 2)2≥0， ∴若a>0时，当x=－a b2 时， y 最小值=a b ac 442-；若a<0时，当x=－ab2 时， y 最大值=a b ac 442-.②判别式法：原函数可化为关于x 的二次方程ax 2+bx+c －y=0. ∵x 在全体实数取值时， ∴ △≥0即b 2－4a(c －y)≥0， 4ay ≥4ac －b 2.若a>0，y ≥a b ac 442-，这时取等号，则y 为最小值a b ac 442-；若a<0，y ≤a b ac 442-，这时取等号，则y 为最大值ab ac 442-.有时自变量x 定在某个区间内取值，求最大、最小值时，要用到临界点，一般用配方法方便.2. 用上述两种方法，可推出如下两个定理：定理一：两个正数的和为定值时，当两数相等时，其积最大. 最大值是定值平方的四分之一.例如：两正数x 和y ， 如果x+y=10, 那么xy 的积有最大值，最大值是25. 定理二：两个正数的积为定值时，当两数相等时，其和最小. 最小值是定值的算术平方根的2倍.例如：两正数x 和y ，如果xy=16, 那么 x+y 有最小值，最小值是8. 证明定理一，可用配方法，也叫构造函数法.设a>0, b>0, a+b=k . (k 为定值).那么ab=a(k －a)=－a 2+ka=－(a －21k)2+42k .当a=2k时，ab 有最大值42k .证明定理二，用判别式法，也叫构造方程法. 设a>0, b>0, ab=k (k 为定值)，再设 y=a+b. 那么y=a+ak , a 2－ya+k=0.（这是关于a 的二次议程方程） ∵ a 为正实数，∴△≥0. 即(－y)2－4k ≥0， y 2－4k ≥0. ∴y ≤－2k (不合题意舍去)； y ≥2k . ∴ y 最小值=2k . 解方程组⎩⎨⎧==+.2k ab k b a ， 得a=b=k .∴当a=b=k 时，a+b 有最小值 2 k . 3. 在几何中，求最大、最小值还有下列定理：定理三：一条边和它的对角都有定值的三角形，其他两边的和有最大值. 当这两边相等时，其和的值最大.定理四：一条边和这边上的高都有定值的三角形，其他两边的和有最小值. 当这两边相等时，其和的值最小.定理五：周长相等的正多边形，边数较多的面积较大；任何正多边形的面积都小于同周长的圆面积.二、例题例1. 已知：3x 2+2y 2=6x, x 和y 都是实数，求：x 2+y 2的最大、最小值.解：由已知y 2=2362x x -, ∵y 是实数， ∴y 2≥0.即2362x x -≥0， 6x －3x 2 ≥0， x 2－2x ≤0.解得 0≤x ≤2.这是在区间内求最大、最小值，一般用配方法，x 2+y 2=x 2+2362x x -=－21( x －3)2+29在区间0≤x ≤2中，当x=2 时，x 2+y 2有最大值 4. ∴当x=0时，x 2+y 2=0是最小值 .例2. 已知：一个矩形周长的数值与它面积的数值相等. 求：这个矩形周长、面积的最小值. 解：用构造方程法.设矩形的长，宽分别为 a, b 其周长、面积的数值为k. 那么2(a+b)=ab=k.即 ⎪⎩⎪⎨⎧==+.21k ab k b a ，∴a 和b 是方程 x 2－21kx+k=0 的两个实数根. ∵a, b 都是正实数，∴△≥0. 即(－2k )2－4k ≥0. 解得k ≥16；或k ≤0 . k ≤0不合题意舍去. ∴当k ≥16取等号时，a+b, ab 的值最小，最小值是16. 即这个矩形周长、面积的最小值是16.例3. 如图△ABC 的边BC=a, 高AD=h, 要剪下一个 矩形EFGH ，问EH 取多少长时，矩形的面积最大？ 最大面积是多少？解：用构造函数法 设EH=x, S 矩形=y, 则GH=xy . ∵△AHG ∽△ABC ，∴hxh a x y-= . ∴ y=4)2()(2ahh x h a h x h ax +--=-. aCEF∴当x=2h 时，y 最大值 =4ah . 即当EH=2h 时，矩形面积的最大值是4ah.例4. 如图已知：直线m ∥n ，A ，B ，C 都是定点，AB=a, AC=b, 点P 在AC 上，BP 的延长线交直线m 于D.问：点P 在什么位置时，S △PAB +S △PCD 最小？ 解：设∠BAC=α，PA=x, 则PC=b －x.∵m ∥n ，∴PA PCAB CD ＝. ∴CD=x x b a )(-S △PAB +S △PCD =21axSin α+21xx b a )(-(b －x) Sin α=21aSin α()222x x bx b x +-+=21aSin α(2x+)22b x b -. ∵2x ×x b 2=2b 2(定值)， 根据定理二，2x +x b 2有最小值.∴ 当2x =x b 2， x=b 221时，S △PAB +S △PCD 的最小值是 (2－1)abSin α. 例5.已知：Rt △ABC 中, 内切圆O 的半径 r=1. 求：S △ABC 的最小值.解：∵S △ABC =21ab ∴ab ＝2S △.∵2r=a+b －c, ∴c=a+b －2r. ∴a+b －2r=22b a + .两边平方，得 a 2+b 2+4r 2+2ab －4(a+b)r= a 2+b 2. 4r 2+2ab －4(a+b)r=0. 用r=1, ab=2S △ 代入， 得 4+4S △－4(a+b) =0. a+b=S △+1. ∵ab=2S △ 且a+b=S △+1.∴a, b 是方程x 2－(S △+1)x+2S △=0 的两个根.nmDa∵a,b 是正实数， ∴△≥0，即 [－(S △+1)]2－4×2S △ ≥0， S △2－6S △+1≥0 .解得 S △≥3+22或S △≤3－22. S △≤3－22不合题意舍去. ∴S △ABC 的最小值是3+22. 例6.已知：.如图△ABC 中，AB=26+，∠C=30 . 求：a+b 的最大值.解：设 a+b=y , 则b=y －a. 根据余弦定理，得 (26+)2=a 2+(y －a)2－2a(y －a)Cos30写成关于a 的二次方程： (2+3)a 2－(2+3)ya+y 2－(8+43)=0.∵a 是实数， ∴△≥0.即(2+3)2y 2－4(2+3)[y 2－(8+43)]≥0，y 2－(8+43)2≤0 .∴ －(8+43)≤y ≤(8+43). ∴a+b 的最大值是8+43.又解：根据定理三 ∵AB 和∠C 都有定值. ∴当a=b 时，a+b 的值最大.由余弦定理，(26+)2=a 2＋b 2－2abCos30可求出 a=b=4+23. ……… 三、练习1. x 1,x 2,x 3,x 4,x 5 满足. x 1+x 2+x 3+x 4+x 5=. x 1x 2x 3x 4x 5，那么. x 5的最大值是＿＿＿＿＿＿.2. 若矩形周长是定值20cm,那么当长和宽分别为____，____时，其面积最大，最大面积是______.3. 面积为100cm 2的矩形周长的最大值是＿＿＿＿＿＿＿＿. 4. a, b 均为正数且a+b=ab,那么 a+b 的最小值 是________.5. 若x>0, 则x+x9的最小值是________. 6.如图直线上有A 、B 、C 、D 四个点.那么到A ，B ，C ，D 距离之和为最小值的点，位于＿＿＿＿＿＿＿＿＿，其和的最小值等于定线段＿＿＿＿＿＿＿＿＿＿＿..7. 如右图△ABC 中，AB=2，AC=3，Ⅰ，Ⅱ，Ⅲ是 以AB ，BC ，CA 为边的正方形，则阴影部份的面积的和的最大值是＿＿＿＿＿＿＿＿＿＿＿＿. 8. 下列四个数中最大的是 ( )（A ） tan48 +cot48 ..(B)sin48 +cos48 . (C) tan48 +cos48 . (D)cot48 +sin48 .9.已知抛物线y=－x 2+2x+8与横轴交于B ，C 两点，点D 平分BC ，若在横轴上侧的点A 为抛物线上的动点，且∠BAC 为锐角，则AD 的取值范围是__________10. 如图△ABC 中，∠C=Rt ∠，CA=CB=1，点P 在AB 上，PQ ⊥BC 于Q.问当P 在AB 上什么位置时，S △APQ 最大？ 11. △ABC 中，AB=AC=a ，以BC 为边向外作等边 三角形BDC ，问当∠BAC 取什么度数时AD 最长？12. 已知x 2+2y 2=1, x,y 都是实数，求2x+5y 2的最大值、最小值. 13. △ABC 中∠B=60，AC=1，求BA+BC 的最大值及这时三角形的形状. 14. 直角三角形的面积有定值k,求它的内切圆半径的最大值.15. D ，E ，F 分别在△ABC 的边BC 、AC 、AB 上，若BD ∶DC=CE ∶EA=AF ∶FA =k ∶(1－k) (0<k<1). 问k 取何值时，S △DEF 的值最小？16.△ABC 中，BC=2，高AD=1，点P ，E ，F 分别在边BC ，AC ，AB 上，且四边形PEAF 是平行四边形.问点P 在BC 的什么位置时，S PEAF 的值最大？C DA B AB参考答案1. 5.2. 5，5 25.3. 40cm4. 45. 66.BC 上，BC+AD.7. 最大值是9，∵S △=21×3×2×SinBAC, ∠BAC=90度时值最大. 8. (A). 9. 3<AD ≤9 10. P 在AB 中点时，S △最大值=81， S △=222x x -⋅x 与2－x 的和有定值， 当x=2－x 时，S △值最大.11. 当∠BAC=120度时，AD 最大，在△ABD 中，设∠BAD=α由正弦定理a Sin ain 230)30180(S AD ==--α，当150 －α=90 时， AD 最大. 12. 当x=52时，有最大值1029；当x=－1时，有最小值－2 (仿例3). 13. 当a=c 时，a+c 有最大值2，这时是等边三角形. 14. 内切圆半径的最大值r=(2－1)△S (仿例6).15. 当 k=21时，S △DEF =41S △ABC ，16.当PB=1时，S 有最大值21. 16. 当点P 是BC 中点时，面积最大值是12.。