2019-2020学年高中数学 正弦函数y=sinx的图像及图像变换课后练习二 新人教A版必修4.doc

（同步复习精讲辅导）北京市2014-2015学年高中数学 正弦函数y=sinx 的图像及图像变换课后练习一 新人教A 版必修4题一题面：在同一个坐标系内画,sin y x y x =-=的图题二题面：在同一个坐标系内画sin ,2x y x y ==的图.题三题面：将函数x y 4sin =的图象向左平移12π个单位，得到)4sin(ϕ+=x y 的图象， 则ϕ等于( )A ．12π- B ．3π- C ．3π D ．12π 题四 题面：在同一个坐标系内画1()sin ,()f x x g x x ==的图 题五题面：函数()yg x =过点(2，1)，则函数1()2y g x =的图像必过的点是 . 题六 题面：试述如何由y =31sin(2x +3π)的图象得到y =sin x 的图象. 题七题面：函数2)62cos(-+=πx y 的图像F 按向量a 平移到F ’，F ’的解析式y =f (x )，当y =f (x )为奇函数时，向量a 可以等于( ) A.)2,6(-π B.)2,6(π C.)2,6(--π D.)2,6(π- 题八题面：已知电流I 与时间t 的关系式为sin()I A t ωϕ=+.(1)下图是sin()I A t ωϕ=+(ω＞0，||2πϕ<)在一个周期内的图象，根据图中数据求sin()I A t ωϕ=+的解析式；(2)如果t 在任意一段1150秒的时间内，电流sin()I A t ωϕ=+都能取得最大值和最小值，那么ω的最小正整数值是多少？课后练习详解题一答案：见详解详解：题二答案：见详解详解：题三答案：C详解：函数x y 4sin =的图象向左平移12π个单位，得到)12(4sin π+=x y 的图象，故3πϕ= 题四答案：见详解详解： 题五答案：(4，1)详解：由题意: (2)1g =， 则1()2yg x =的图像必过的点是(4，1) 题六答案：见详解.详解： y =31sin(2x +3π)）（纵坐标不变倍横坐标扩大为原来的3πsin 312+=−−−−−−−−−→−x y 题七答案：D详解：∵cos(2)26y x π=+-，所以将函数cos(2)26y x π=+-向左平移6π个单位 得到cos 2()2cos(2)2sin 221262y x x x πππ=++-=+-=--，再向上平移2个单位 得到 y =sin2x ，是奇函数，所以由平面向量平行规律可知，(,2)6a π=-，故选D.题八 答案：(1)300sin(150)6I t ππ=+(2)ω＝943详解： (1)由图可知 A ＝300 设t 1＝－1900，t 2＝1180， 则周期T ＝2(t 2－t 1)＝2(1180＋1900)＝175∴ ω＝2Tπ＝150π 又当t ＝1180时，I ＝0，即sin (150π·1180＋ϕ)＝0， 而||2πϕ<， ∴ ϕ＝6π. 故所求的解析式为300sin(150)6I t ππ=+. (2)依题意，周期T ≤1150，即2πω≤1150，(ω>0) ∴ ω≥300π＞942，又ω∈N *，故最小正整数ω＝943.。

正弦函数测试题及答案高中1. 正弦函数的定义是什么？2. 正弦函数的周期是多少？3. 正弦函数的图像有什么特点？4. 正弦函数的奇偶性如何？5. 正弦函数的值域是什么？6. 写出正弦函数的基本公式。

7. 解释正弦函数在三角恒等式中的作用。

8. 给定一个角度，如何计算其正弦值？9. 解释正弦函数在实际问题中的应用。

10. 给出一个正弦函数的图像，判断其振幅、周期和相位。

答案1. 正弦函数的定义是：对于任意角度 \( \theta \)，正弦函数 \( y = \sin(\theta) \) 表示在直角三角形中，对应角度 \( \theta \)的对边与斜边的比值。

2. 正弦函数的周期是 \( 2\pi \) 弧度，或者 \( 360^\circ \)。

3. 正弦函数的图像是一个周期性的波动曲线，它在 \( -1 \) 和\( 1 \) 之间波动，并且关于原点对称。

4. 正弦函数是奇函数，即 \( \sin(-\theta) = -\sin(\theta) \)。

5. 正弦函数的值域是 \( [-1, 1] \)。

6. 正弦函数的基本公式包括：\( \sin(\theta) =\cos(\frac{\pi}{2} - \theta) \) 和 \( \sin(2\theta) =2\sin(\theta)\cos(\theta) \)。

7. 在三角恒等式中，正弦函数用于表达角度之间的关系，如和角公式、差角公式等。

8. 给定角度的正弦值可以通过查找三角函数表、使用计算器或利用单位圆来计算。

9. 正弦函数在实际问题中应用广泛，如物理学中的振动问题、电子学中的交流电问题等。

10. 正弦函数的图像可以通过振幅 \( A \)，周期 \( T \) 和相位\( \phi \) 来描述，公式为 \( y = A\sin(\omega x + \phi) \)，其中 \( A \) 是振幅，\( T = \frac{2\pi}{\omega} \) 是周期，\( \omega \) 是角频率，\( \phi \) 是相位。

y=sinx 的图像及图像变换讲义 新人教A 版必修4重难点易错点解析在恰当的坐标系中画正弦函数的图题一题面：在同一个坐标系内画,sin y x y x ==的图题二题面：在同一个坐标系内画sin ,lg y x y x ==的图真正理解图像变换题三题面：把曲线y cos x +2y －1=0先沿x 轴向右平移2π个单位，再沿y 轴向下平移1个单位，得到的曲线方程是( )A.(1－y )sin x +2y －3=0B.(y －1)sin x +2y －3=0C.(y +1)sin x +2y +1=0D.－(y +1)sin x +2y +1=0金题精讲题一 题面：在同一个坐标系内画sin ,100x y x y ==的图题二题面：函数)4(x f y =过点(3，1)，则函数)22(+=x f y 的图像必过的点是 . 题三题面：如何由函数x y sin =的图象变换得到)42sin(π+=x y 的图象.下面三条路，你选哪条？为什么？ sin sin 2sin(2)4y x y x y x π=→=→=+ sin sin()sin(2)84y x y x y x ππ=→=+→=+ sin sin()sin(2)44y x y x y x ππ=→=+→=+ 题四题面：如何由函数x y sin =的图象变换得到2sin(2)14y x π=++的图象. 思维拓展题一题面：已知函数()()()22sin 122x f x x x x π=+-+. (1)那么方程()0f x =在区间[100,100]-上的根的个数是__________．(2)对于下列命题：①函数()f x 是周期函数；②函数()f x 既有最大值又有最小值；③函数()f x 的定义域是R ，且其图象有对称轴；④函数()f x 在(1,0)-上是减函数.其中真命题的序号是 ．(填写出所有真命题的序号)讲义参考答案重难点易错点解析题一答案：题二答案：题三答案：C金题精讲题一答案：草图供参考图略，一共有63个交点。

正弦函数、余弦函数的图像(附答案)海黄和紫檀哪个更有价值怕上当受骗，我们教你如何鉴别小叶紫檀的真伪！点击访问：木缘鸿官网北京十里河古玩市场，美不胜收的各类手串让记者美不胜收。

“黄花梨和紫檀是数一数二的好料，市场认可度又高，所以我们这里专注做这两种木料的手串。

”端木轩的尚女士向记者引见说。

海黄紫檀领风骚手串是源于串珠与手镯的串饰品，今天曾经演化为集装饰、把玩、鉴赏于一体的特征珍藏品。

怕上当受骗，我们教你如何鉴别小叶紫檀的真伪！点击访问：木缘鸿官网“目前珍藏、把玩木质手串的人越来越多，特别是海黄和印度小叶檀最受藏家追捧，有人把黄花梨材质的手串叫做腕中黄金。

”纵观海南黄花梨近十年的价钱行情，不难置信尚女士所言非虚。

一位从事黄花梨买卖多年的店主夏先生通知记者，在他的记忆中，2000年左右黄花梨上等老料的价钱仅为60元/公斤，2002年大量收购时，价格也仅为2万元/吨左右，而往常，普通价钱坚持在7000-8000元/公斤，好点的1公斤料就能过万。

“你看这10年间海南黄花梨价钱涨了百余倍，都说水涨船高，这海黄手串的价钱自然也是一路飙升。

”“这串最低卖8000元，能够说是我们这里海黄、小叶檀里的一级品了，普通这种带鬼脸的海黄就是这个价位。

”檀梨总汇的李女士说着取出手串让记者感受一下，托盘里一串直径2.5mm的海南黄花梨手串熠熠生辉，亦真亦幻的自然纹路令人入迷。

当问到这里最贵的海黄手串的价钱时，李女士和记者打起了“太极”，几经追问才通知记者，“有10万左右的，普通不拿出来”。

同海南黄花梨并排摆放的是印度小叶檀手串，价位从一串三四百元到几千元不等。

李女士引见说，目前市场上印度小叶檀原料售价在1700元/公斤左右，带金星的老料售价更高，固然印度小叶檀手串的整体售价不如海黄手串高，但近年来有的也翻了数十倍，随着老料越来越少，未来印度小叶檀的升值空间很大。

“和海黄手串比起来，印度小叶檀的价钱相对低一些，普通买家能消费得起。

2019-2020年高中数学第一章三角函数1.5正弦函数的图像与性质课后导练北师大版必修基础达标1.sin600°的值是（）A. B.- C. D.解析：利用诱导公式2kπ+α，将sin600°化为sin(600°-2×360°).sin600°=sin(600°-720°)=sin(-120°)=.答案：D2.若sin（π-α）=，则sin（-5π+α）的值为（）A. B. C.± D.0解析:化简已知和结论，易找出条件和结论的关系.由sin（π-α）=，知sinα=，而sin（-5π+α）=sin（-6π+π+α）=sin（π+α）=-sinα.∴sin(-5π+α)=.答案：B3.角α终边有一点P（t,t）(t≠0),则sinα的值是（）A. B. C.± D.1解析：因P（t,t）,∴P在第一或第三象限的角平分线上，∴sinα=±.答案：C4.函数y=的定义域是（）A.［kπ-,kπ+］，(k∈Z)B.［2kπ+,2kπ+π］，(k∈Z)C.［kπ+,(k+1)π］，(k∈Z)D.［2kπ,2kπ+π］，(k∈Z)解析：由sinx≥0知2kπ≤α≤2kπ+π(k∈Z).答案：D5.y=属于（）A.{1，-1}B.{1}C.{-1}D.{1，0，-1}解析：当sinx＞0时，y=1;当sinx＜0时，y=-1,故y∈{-1,1}.答案：A6.已知角θ的终边落在y=2x上，则sinα=_________.解析：取y=2x上的点（1，2），则r=,∴sinα=,同理取点（-1,-2），得sinα=.答案：±7.若x∈［-π，π］，且sinx=，则x等于…（）A.或B.-或C.或D.或-解析:考虑到是特殊值，因此角x必为特殊角，可先确定出符合条件的最小正角.由于sinx=，所以x的终边落在第三或第四象限.在［-π，π］内，只有-和.答案：D8.设sinx=t-3，则t的取值范围是（）A.RB.（2，4）C.（-2，2）D.［2，4］解析：当x∈R时,-1≤sinx≤1,∴-1≤t-3≤1,∴2≤t≤4.答案：D9.判断下列函数的奇偶性.(1)f(x)=xsin(π+x)；(2)f(x)=.解析：(1)函数的定义域为R，关于原点对称.f(x)=xsin(π+x)=-xsinx,f(-x)=-(-x)sin(-x)=-xsinx=f(x)∴f(x)是偶函数.(2)∵sinx-1≥0,∴sinx=1,x=2kπ+,(k∈Z),函数定义域是不关于原点对称的区间，故为非奇非偶函数.10.求下列函数的周期.(1)y=sinx；(2)y=2sin().解析：(1)如果令m=x,则sinx=sinm是周期函数，且周期为2π.∴sin(x+2π)=sinx,即sin［(x+4π)］=sinx,∴sin12x的周期4π.(2)∵2sin(+2π)=2sin(),即2sin［(x+6π)-］=2sin(),∴2sin()的周期是6π.综合运用11.若sinx＞，则x满足（）A.k·360°+60°＜x＜k·360°+120°B.60°＜x＜120°C.k·360°+15°＜x＜k·360°+75°D.k·180°+30°＜x＜k·180°+150°解析:可借助于单位圆中的正弦线或三角函数图象来解决.画出单位圆或正弦曲线草图，可确定满足sinx＞的x应是k·360°+60°＜x＜k·360°+120°.答案：A12.下列函数中，周期为π、图象关于直线x=对称的函数是（）A.y=2sin(+)B.y=2sin(-)C.y=sin(2x+)D.y=sin(2x-)解析:sin(ωx+φ)的周期是，对称轴方程是ωx+φ=kπ+(k∈Z),由周期为π,排除A、B.将x=代入2x+得,将x=代入2x-得，故选D.答案：D13.用五点法作y=2sin2x的图象时，首先应描出的五点的横坐标可以是（）A.0，，π，，2πB.0，，，，πC.0，π，2π，3π，4πD.0，，，，解析：先写出y=sinx五点的横坐标.0，π,,2π.当2x=0时，x=0;当2x=时，x=;当2x=π时，x=;当2x=时，x=;当2x=2π时，x=π,故选B.答案：B14.y=|sinx|+sinx的值域是________.解析：当sinx≥0时，y=2sinx,这时0≤y≤2;当sinx＜0时，y=0,∴函数的值域是［0，2］.答案：［0,2］15.以一年为一个周期调查某商品出厂价及该商品在商店的销售价格时发现：该商品的出厂价是在6元的基础上按月份随正弦曲线波动的.已知3月份出厂价最高为8元，7月份出厂价最低为4元；而该商品在商店内的销售价格是在9元的基础上也是按月份随正弦曲线波动的，并且已知3月份价格最高为10元，7月份价格最低为8元.假设某商店每月购进这种商品m件，且当月能售完，请估计哪个月份赢利最大，并说明理由.解析：由条件得：出厂价格函数是y1=2sin(x-)+6；销售价格函数为y2=sin(x-)+9.则利润函数为y=m(y2-y1).=m［sin(x-)+9-2sin(x-)-6］=m［3-sin(x-)］.所以当x=7时,y=4m.所以7月份赢利最大.拓展探究16.烟筒弯头是由两个圆柱形的烟筒焊在一起做成的，现在要用长方形铁皮做成一个直角烟筒弯头（两个圆柱呈垂直状），如右图，若烟筒的直径为12 cm，最短母线为6 cm，应将铁皮如何剪裁，才能既省工又省料？解析：如下图（2）所示，两个圆柱形烟筒的截面与水平面成45°角，设O是圆柱的轴与截面的交点，过O作水平面，它与截面的交线为CD，它与圆柱的交线是以O为圆心的圆，CD 是此圆的直径.又设B是这个圆上任意一点，过B作BE垂直CD于E，作圆柱的母线AB，交截平面与圆柱的交线于A，易知∠AEB=45°，所以AB=BE.设BD弧长为x，它所取的圆心角∠DOB=α，根据弧长公式，知α=.又设AB=y，在Rt△BOE 中，sinα=，故BE=6sinα，从而y=AB=BE=6sinα，即y=6sin.所以，铁皮在接口处的轮廓线是正弦曲线y=6sin(0≤x≤12π)，其图象如下图（4）.因为将两个圆柱形铁皮上的曲线对拼起来，正好可以完全吻合，所以最节约且最省工的裁剪方式如下图（5）.。

7．3.2 正弦型函数的性质与图像［课程目标］1。

了解正弦型函数y＝A sin（ωx＋φ)的实际意义及各参数对图像变化的影响，会求其周期、最值、单调区间等．2．会用“五点法”及“图像变换法”作正弦型函数y＝A sin(ωx＋φ)的图像．［填一填］1．正弦型函数（1）形如y＝A sin(ωx＋φ)（其中A，ω,φ都是常数,且A≠0，ω≠0)的函数，通常叫做正弦型函数．（2）函数y＝A sin（ωx＋φ)(其中A≠0，ω>0，x∈R）的周期T＝错误!,频率f＝错误!，初相为φ，值域为[－｜A|，|A｜］，｜A|也称为振幅,|A|的大小反映了y＝A sin（ωx＋φ）的波动幅度的大小．2．正弦型函数的性质正弦型函数y＝A sin（ωx＋φ)( A〉0,ω〉0）有如下性质．(1）定义域:R。

(2)值域：［－A，A]．(3）周期:T＝错误!。

(4)单调区间：单调增区间由2kπ－错误!≤ωx＋φ≤2kπ＋错误!(k∈Z）求得，单调减区间由2kπ＋π2≤ωx＋φ≤2kπ＋32π(k∈Z）求得．3．利用图像变换法作y＝A sin（ωx＋φ)＋b的图像［答一答] 1．怎样得到y＝A sin（ωx＋φ)的图像？提示:(1)“五点法”画函数y＝A sin(ωx＋φ)的图像：画函数y＝A sin(ωx＋φ）的简图,主要是先找出确定曲线形状时起关键作用的五个点．这五个点应该是使函数取得最大值、最小值及曲线与x轴相交的点，找出它们的方法是作变量代换．设X＝ωx＋φ，由X取0，错误!，π，错误!，2π来确定对应的x 值．(2）由函数y＝sin x图像变换到y＝A sin(ωx＋φ)的图像:步骤1:画出正弦曲线在长度为2π的某闭区间上的简图．步骤2：沿x轴平行移动，得到y＝sin(x＋φ）在长度为2π的某闭区间上的简图．步骤3：横坐标伸长或缩短，得到y＝sin（ωx＋φ)在长度为一个周期的闭区间上的简图．步骤4：纵坐标伸长或缩短,得到y＝A sin(ωx＋φ)在长度为一个周期的闭区间上的简图．步骤5：沿x轴伸展,得到y＝A sin（ωx＋φ），x∈R的简图．上述变换步骤概括如下：步骤1错误!步骤2错误!步骤3错误!步骤4―→步骤5其中相位变换中平移量为｜φ|单位,φ>0时向左移，φ<0时向右移;周期变换中的纵坐标不变,横坐标变为原来的错误!倍；振幅变换中，横坐标不变，而纵坐标变为原来的A倍．2．三角函数图像的平移变换和伸缩变换的规律是什么?提示：(1）平移变换：①沿x轴平移，按“左加右减"规律；②沿y轴平移，按“上加下减"规律．（2）伸缩变换:①沿x轴伸缩：ω>1时,横坐标缩短到原来的错误!倍，0<ω〈1时,横坐标伸长到原来的1ω倍，纵坐标保持不变；②沿y轴伸缩：当A>1时，把纵坐标伸长到原来的A倍,当0〈A〈1时，纵坐标缩短到原来的A倍，横坐标保持不变．3．怎样由图像或部分图像求正弦函数y＝A sin（ωx＋φ）的解析式？提示：关键在于确定参数A，ω，φ。

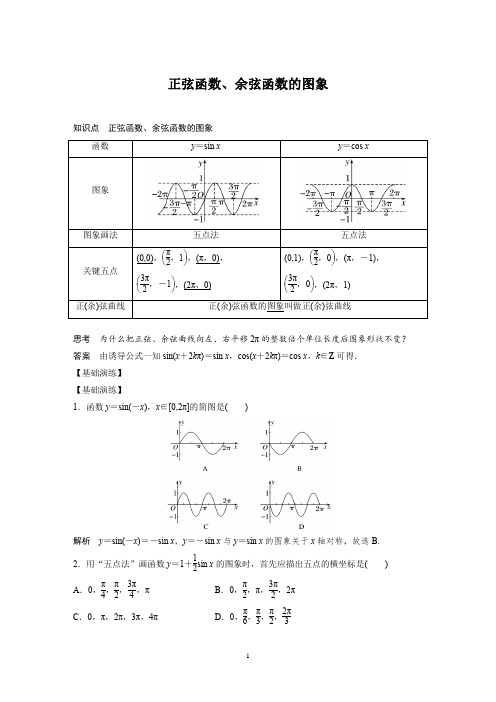
正弦函数、余弦函数的图象知识点正弦函数、余弦函数的图象五点法五点法思考为什么把正弦、余弦曲线向左、右平移2π的整数倍个单位长度后图象形状不变？答案由诱导公式一知sin(x＋2kπ)＝sin x，cos(x＋2kπ)＝cos x，k∈Z可得．【基础演练】【基础演练】1．函数y＝sin(－x)，x∈[0,2π]的简图是()解析y＝sin(－x)＝－sin x，y＝－sin x与y＝sin x的图象关于x轴对称，故选B.2．用“五点法”画函数y＝1＋12sin x的图象时，首先应描出五点的横坐标是() A．0，π4，π2，3π4，π B．0，π2，π，3π2，2πC．0，π，2π，3π，4π D．0，π6，π3，π2，2π3解析 所描出的五点的横坐标与函数y ＝sin x 的五点的横坐标相同，即0，π2，π，3π2，2π，故选B.3．在同一平面直角坐标系内，函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象( ) A ．重合 B ．形状相同，位置不同 C ．关于y 轴对称 D ．形状不同，位置不同答案 B解析 根据正弦曲线的作法可知函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象只是位置不同，形状相同． 4．在[0,2π]内，不等式sin x <－32的解集是( ) A ．(0，π) B.⎝⎛⎭⎫π3，4π3 C.⎝⎛⎭⎫4π3，5π3 D.⎝⎛⎭⎫5π3，2π 解析 画出y ＝sin x ，x ∈[0,2π]的草图如下．当sin x ＝－32时，x ＝4π3或x ＝5π3， 可知不等式sin x <－32在[0,2π]上的解集是⎝⎛⎭⎫4π3，5π3.故选C. 5．函数y ＝cos x ＋4，x ∈[0,2π]的图象与直线y ＝4的交点的坐标为________．解析 由⎩⎪⎨⎪⎧y ＝cos x ＋4，y ＝4得cos x ＝0，当x ∈[0,2π]时，x ＝π2或3π2，∴交点坐标为⎝⎛⎭⎫π2，4，⎝⎛⎭⎫3π2，4.【典型例题】考点一：正弦函数、余弦函数图象的初步认识 例1 (1)下列叙述正确的个数为( )①y ＝sin x ，x ∈[0,2π]的图象关于点P (π，0)成中心对称； ②y ＝cos x ，x ∈[0,2π]的图象关于直线x ＝π成轴对称；③正弦、余弦函数的图象不超过直线y ＝1和y ＝－1所夹的范围． A ．0 B ．1 C ．2 D ．3解析 分别画出函数y ＝sin x ，x ∈[0,2π]和y ＝cos x ，x ∈[0,2π]的图象，由图象(略)观察可知①②③均正确．答案 D(2)函数y ＝sin |x |的图象是( )答案 B解析 y ＝sin |x |＝⎩⎪⎨⎪⎧sin x ，x ≥0，－sin x ，x <0，结合选项可知选B.反思感悟 解决正弦、余弦函数图象的注意点对于正弦、余弦函数的图象问题，要画出正确的正弦曲线、余弦曲线，掌握两者的形状相同，只是在坐标系中的位置不同，可以通过相互平移得到．跟踪训练1 下列关于正弦函数、余弦函数的图象的描述，不正确的是( ) A ．都可由[0,2π]内的图象向上、向下无限延展得到 B ．都是对称图形 C ．都与x 轴有无数个交点D ．y ＝sin(－x )的图象与y ＝sin x 的图象关于x 轴对称 答案 A解析 由正弦、余弦函数图象知，B ，C ，D 正确．考点二：用“五点法”作三角函数的图象 例2 用“五点法”作出下列函数的简图： (1)y ＝sin x －1，x ∈[0,2π]； (2)y ＝－2cos x ＋3，x ∈[0,2π]． 解 (1)列表：描点并将它们用光滑的曲线连接起来，如图．(2)列表：描点、连线得出函数y＝－2cos x＋3，x∈[0,2π]的图象．反思感悟作形如y＝a sin x＋b(或y＝a cos x＋b)，x∈[0,2π]的图象的三个步骤跟踪训练2利用“五点法”作出函数y＝2＋cos x(0≤x≤2π)的简图．解列表：描点并将它们用光滑的曲线连接起来，如图．考点三：正弦函数、余弦函数图象的应用 例3 不等式2sin x －1≥0，x ∈[0,2π]解集为( ) A.⎣⎡⎦⎤0，π6 B.⎣⎡⎦⎤0，π4 C.⎣⎡⎦⎤π6，π D.⎣⎡⎦⎤π6，5π6答案 D解析 因为2sin x －1≥0，所以sin x ≥12.在同一直角坐标系下，作函数y ＝sin x ，x ∈[0,2π]以及直线y ＝12的图象．由函数的图象知，sin π6＝sin 5π6＝12.所以根据图象可知，sin x ≥12的解集为⎣⎡⎦⎤π6，5π6. 延伸探究1．在本例中把“x ∈[0,2π]”改为“x ∈R ”，求不等式2sin x －1≥0的解集． 解 在x ∈[0,2π]上的解集为⎣⎡⎦⎤π6，5π6.所以x ∈R 时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6＋2k π≤x ≤5π6＋2k π，k ∈Z . 2．试求关于x 的不等式12<sin x ≤32.解 作出正弦函数y ＝sin x 在[0,2π]上的图象，作出直线y ＝12和y ＝32，如图所示．由图可知，在[0,2π]上当π6<x ≤π3或2π3≤x <5π6时，不等式12<sin x ≤32成立，所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6＋2k π<x ≤π3＋2k π或2π3＋2k π≤x <5π6＋2k π，k ∈Z . 反思感悟 利用三角函数图象解三角不等式sin x >a (cos x >a )的步骤 (1)作出相应的正弦函数或余弦函数在[0,2π]上的图象． (2)确定在[0,2π]上sin x ＝a (cos x ＝a )的x 值． (3)写出不等式在区间[0,2π]上的解集． (4)根据公式一写出定义域内的解集．跟踪训练3 求函数y ＝1－2cos x 的定义域． 解 依题意有1－2cos x ≥0，即cos x ≤12.作出余弦函数y ＝cos x ，x ∈[0,2π]以及直线y ＝12的图象，如图所示，由图象可以得到满足条件的x 的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪π3＋2k π≤x ≤5π3＋2k π，k ∈Z .根据函数图象求范围典例 函数f (x )＝sin x ＋2|sin x |，x ∈[0,2π]的图象与直线y ＝k 有且仅有两个不同的交点，则k 的取值范围是________． 答案 (1,3)解析 f (x )＝⎩⎪⎨⎪⎧3sin x ，0≤x ≤π，－sin x ，π<x ≤2π.图象如图所示．结合图象可知1<k <3.[素养提升] 关于方程根的个数问题，往往运用数形结合的方法构造函数，转化为函数图象交点的个数问题来解决，体现了直观想象的核心素养．1．(多选)用五点法画y ＝3sin x ，x ∈[0,2π]的图象时，下列哪个点不是关键点( ) A.⎝⎛⎭⎫π6，32 B.⎝⎛⎭⎫π2，3 C ．(π，0) D ．(2π，3) 答案 AD解析 五个关键点的横坐标依次是0，π2，π，3π2，2π.代入计算得B ，C 是关键点．2．已知函数f (x )＝sin ⎝⎛⎭⎫x ＋π2，g (x )＝cos ⎝⎛⎭⎫x －π2，则f (x )的图象( ) A ．与g (x )的图象相同 B ．与g (x )的图象关于y 轴对称C ．向左平移π2个单位长度，得g (x )的图象D ．向右平移π2个单位长度，得g (x )的图象答案 D解析 f (x )＝sin ⎝⎛⎭⎫x ＋π2，g (x )＝cos ⎝⎛⎭⎫x －π2＝cos ⎝⎛⎭⎫π2－x ＝sin x ， f (x )的图象向右平移π2个单位长度得到g (x )的图象．3．在[0,2π]上，函数y ＝2sin x －2的定义域是( ) A.⎣⎡⎦⎤0，π4 B.⎣⎡⎦⎤π4，3π4 C.⎣⎡⎦⎤π4，π2D.⎣⎡⎦⎤3π4，π解析 依题意得2sin x －2≥0，即sin x ≥22.作出y ＝sin x 在[0,2π]上的图象及直线y ＝22，如图所示．由图象可知，满足sin x ≥22的x 的取值范围是⎣⎡⎦⎤π4，3π4，故选B. 4．函数y ＝1＋sin x ，x ∈[0,2π]的图象与直线y ＝12交点的个数是( )A ．0B ．1C ．2D ．3 答案 C解析 由函数y ＝1＋sin x ，x ∈[0,2π]的图象(如图所示)，可知其与直线y ＝12有2个交点．5．函数f (x )＝sin x －1，x ∈[0,2π]的零点为________． 答案 π2解析 令f (x )＝0，∴sin x ＝1，∴又x ∈[0,2π]，∴x ＝π2.6．已知函数f (x )＝2cos x ＋1，若f (x )的图象过点⎝⎛⎭⎫π2，m ，则m ＝________；若f (x )<0，则x 的取值集合为________．答案 1 ⎩⎨⎧⎭⎬⎫x ⎪⎪2π3＋2k π<x <4π3＋2k π，k ∈Z 解析 当x ＝π2时，f (x )＝2cos π2＋1＝1，∴m ＝1.f (x )<0，即cos x <－12，作出y ＝cos x 在x ∈[0,2π]上的图象，如图所示．由图知x 的取值集合为⎩⎨⎧⎭⎬⎫x ⎪⎪2π3＋2k π<x <4π3＋2k π，k ∈Z . 7．根据y ＝cos x 的图象解不等式：－32≤cos x ≤12，x ∈[0，2π]． 解 函数y ＝cos x ，x ∈[0,2π]的图象如图所示：根据图象可得不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3≤x ≤5π6或7π6≤x ≤5π3.8．(多选)函数y ＝sin x －1，x ∈[0,2π]与y ＝a 有一个交点，则a 的值为( ) A ．－1 B ．0 C ．1 D ．－2 答案 BD解析 画出y ＝sin x －1的图象．如图．依题意a ＝0或a ＝－2.9．函数y ＝cos x ＋|cos x |，x ∈[0,2π]的大致图象为( )答案 D解析 由题意得y ＝⎩⎨⎧2cos x ，0≤x ≤π2或3π2≤x ≤2π，0，π2<x <3π2.10．函数f (x )＝lg cos x ＋25－x 2的定义域为________________． 答案 ⎣⎡⎭⎫－5，－3π2∪⎝⎛⎭⎫－π2，π2∪⎝⎛⎦⎤3π2，5 解析 由题意，得x 满足不等式组⎩⎪⎨⎪⎧ cos x >0，25－x 2≥0，即⎩⎪⎨⎪⎧cos x >0，－5≤x ≤5，作出y ＝cos x 的图象，如图所示．结合图象可得x ∈⎣⎡⎭⎫－5，－3π2∪⎝⎛⎭⎫－π2，π2∪⎝⎛⎦⎤3π2，5.11．函数y ＝2cos x ，x ∈[0,2π]的图象和直线y ＝2围成的一个封闭的平面图形的面积是________． 答案 4π解析 如图所示，将余弦函数的图象在x 轴下方的部分补到x 轴的上方，可得一个矩形，其面积为2π×2＝4π.12．若方程sin x ＝1－a 2在x ∈⎣⎡⎦⎤π3，π上有两个实数根，求a 的取值范围． 解 在同一直角坐标系中作出y ＝sin x ，x ∈⎣⎡⎦⎤π3，π的图象，y ＝1－a2的图象，由图象可知，当32≤1－a2<1，即当－1<a ≤1－3时，y ＝sin x ，x ∈⎣⎡⎦⎤π3，π的图象与y ＝1－a 2的图象有两个交点，即方程sin x ＝1－a 2在x ∈⎣⎡⎦⎤π3，π上有两个实数根．。

7.3三角函数的性质与图像7.3.1正弦函数的性质与图像学习目标核心素养1.理解正弦函数的性质，会求正弦函数的定义域和值域、最小正周期、奇偶性、单调区间及函数的零点．(重点)2.能正确使用“五点法”作出正弦函数的图像．(难点)1.借助正弦函数图像和性质的应用，培养学生的直观想象、逻辑推理及数学运算核心素养．2.通过正弦函数图像和性质的学习，培养学生的直观想象核心素养.1.正弦函数的性质(1)函数的周期性①周期函数：对于函数f(x)，如果存在一个非零常数T，使得对定义域内的每一个x，都满足f(x＋T)＝f(x)，那么就称函数f(x)为周期函数，非零常数T称为这个函数的周期．②最小正周期：对于一个周期函数f(x)，如果在它的所有周期中存在一个最小的正数，那么这个最小的正数就称为f(x)的最小正周期．(2)正弦函数的性质函数y＝sin x定义域R值域[－1,1]奇偶性奇函数周期性最小正周期：2π单调性在⎣⎢⎡⎦⎥⎤2kπ－π2，2kπ＋π2(k∈Z)上递增；在⎣⎢⎡⎦⎥⎤2kπ＋π2，2kπ＋32π(k∈Z)上递减最值x ＝2k π＋π2 ，(k ∈Z )时，y 最大值＝1； x ＝2k π－π2(k ∈Z )时，y 最小值＝－1(1)利用正弦线可以作出y ＝sin x ，x ∈[0,2π]的图像，要想得到y ＝sin x (x ∈R )的图像，只需将y ＝sin x ，x ∈[0,2π]的图像沿x 轴平移±2π，±4π，…即可，此时的图像叫做正弦曲线．(2)“ 五点法” 作y ＝sin x ，x ∈[0,2π]的图像时，所取的五点分别是(0,0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，和⎝ ⎛⎭⎪⎫32π，－1和(2π，0)． 思考：观察正弦函数的图像是否具有对称性，它的对称性是怎样的？ [提示] 由图(图略)可以看出，正弦函数的图像关于原点成中心对称，除了原点这个对称点外，对于正弦函数图像，点(π，0)，点(2π，0)… ，点(k π，0)也是它的对称中心，由此正弦函数图像有无数个对称中心，且为(k π，0)(k ∈Z )，即图像与x 轴的交点，正弦函数的图像还具有轴对称性，对称轴是x ＝k π＋π2 ，(k ∈Z )，是过图像的最高或最低点，且与x 轴垂直的直线．1.函数y ＝x sin x 是( ) A ．奇函数，不是偶函数 B ．偶函数，不是奇函数 C ．奇函数，也是偶函数D ．非奇非偶函数B [f (－x )＝－x sin(－x )＝－x (－sin x )＝x sin x ＝f (x )，∴y ＝x sin x 为偶函数，不是奇函数．]2.下列图像中，符合y ＝－sin x 在[0,2π]上的图像的是( )D [把y ＝sin x ，x ∈[0,2π]上的图像关于x 轴对称，即可得到y ＝－sin x ，x ∈[0,2π]上的图像，故选D ．]3.点M ⎝ ⎛⎭⎪⎫π2，－m 在函数y ＝sin x 的图像上，则m 等于( )A ．0B ．1C ．－1D ．2C [由题意－m ＝sin π2，∴－m ＝1， ∴m ＝－1.]三角函数奇偶性的判定(1)f (x )＝sin ⎝ ⎛⎭⎪⎫－12x ＋π2；(2)f (x )＝lg(1－sin x )－lg(1＋sin x )． [解](1)显然x ∈R ，f (x )＝cos 12x ， ∵f (－x )＝cos ⎝ ⎛⎭⎪⎫－12x ＝cos 12x ＝f (x )，∴f (x )是偶函数．(2)由⎩⎪⎨⎪⎧1－sin x >0，1＋sin x >0，得－1<sin x <1.解得定义域为⎩⎨⎧⎭⎬⎫x |x ∈R 且x ≠k π＋π2，k ∈Z . ∴f (x )的定义域关于原点对称． 又∵ f (x )＝lg(1－sin x )－lg(1＋sin x )，∴ f (－x )＝lg[1－sin(－x )]－lg[1＋sin(－x )] ＝lg(1＋sin x )－lg(1－sin x )＝－f (x )． ∴f (x )为奇函数．判断函数奇偶性应把握好两个关键点： 关键点一：看函数的定义域是否关于原点对称； 关键点二：看f (x )与f (－x )的关系.对于三角函数奇偶性的判断，有时可根据诱导公式先将函数式化简后再判断.1.判断函数f (x )＝cos ⎝ ⎛⎭⎪⎫3π2＋2x ＋x 2sin x 的奇偶性．[解] 原式＝sin 2x ＋x 2sin x ，又∵x ∈R ，f (－x )＝sin(－2x )＋(－x )2sin(－x ) ＝－sin 2x －x 2sin x ＝－f (x )， ∴f (x )是奇函数.正弦函数的单调性及应用(1)sin 194°和cos 160°； (2)sin 74和cos 53.[思路探究] 先化为同一单调区间上的同名函数，然后利用单调性来比较函数值的大小．[解](1)sin 194°＝sin(180°＋14°)＝－sin 14°. cos 160°＝cos(180°－20°)＝－cos 20°＝－sin 70°. ∵0°<14°<70°<90°，∴sin 14°<sin 70°.从而－sin 14°>－sin 70°，即sin 194°>cos 160°. (2)∵cos 53＝sin ⎝ ⎛⎭⎪⎫π2＋53，又π2<74<π<π2＋53<32π，y ＝sin x 在⎣⎢⎡⎦⎥⎤π2，32π上是减函数，∴sin 74>sin ⎝ ⎛⎭⎪⎫π2＋53＝cos 53，即sin 74>cos 53.比较三角函数值的大小时，需要把角化为同一单调区间上的同名三角函数，然后用三角函数的单调性即可，如果角不在同一单调区间上，一般用诱导公式进行转化，然后再比较.2.比较大小：(1)sin 250°与sin 260°； (2)sin ⎝ ⎛⎭⎪⎫－235π与sin ⎝ ⎛⎭⎪⎫－174π.[解](1)sin 250°＝sin(180°＋70°)＝－sin 70°，sin 260°＝sin(180°＋80°)＝－sin 80°，因为0°＜70°＜80°＜90°，且函数y ＝sin x ，x ∈⎣⎢⎡⎦⎥⎤0，π2是增函数，所以sin 70°＜sin 80°，所以－sin 70°＞－sin 80°，即sin 250°＞sin 260°. (2)sin ⎝ ⎛⎭⎪⎫－23π5＝－sin 23π5＝－sin 3π5＝－sin ⎝ ⎛⎭⎪⎫π－2π5＝－sin 2π5.sin ⎝ ⎛⎭⎪⎫－17π4＝－sin 17π4＝－sin π4. 因为0＜π4＜2π5＜π2，且函数y ＝sin x ，x ∈⎣⎢⎡⎦⎥⎤0，π2是增函数，所以sin π4＜sin 2π5，－sin π4>－sin 2π5， 即sin ⎝ ⎛⎭⎪⎫－23π5＜sin ⎝ ⎛⎭⎪⎫－17π4.正弦函数的值域与最值问题(1)y ＝3＋2sin ⎝ ⎛⎭⎪⎫2x －π3；(2)y ＝1－2sin 2x ＋sin x .[思路探究](1)用|sin α|≤1构建关于y 的不等式，从而求得y 的取值范围． (2)用t 代替sin x ，然后写出关于t 的函数，再利用二次函数的性质及|t |≤1即可求出y 的取值范围．[解](1)∵－1≤sin ⎝ ⎛⎭⎪⎫2x －π3≤1，∴－2≤2sin ⎝ ⎛⎭⎪⎫2x －π3≤2，∴1≤2sin ⎝ ⎛⎭⎪⎫2x －π3＋3≤5， ∴1≤y ≤5，即函数y ＝3＋2sin ⎝ ⎛⎭⎪⎫2x －π3的值域为[1,5]．(2)y ＝1－2sin 2x ＋sin x ， 令sin x ＝t ，则－1≤t ≤1， y ＝－2t 2＋t ＋1＝－2⎝ ⎛⎭⎪⎫t －142＋98.由二次函数y ＝－2t 2＋t ＋1的图像可知－2≤y ≤98，即函数y ＝1－2sin 2x ＋sin x 的值域为⎣⎢⎡⎦⎥⎤－2，98.1.换元法，旨在三角问题代数化，要防止破坏等价性．2.转化成同一函数，要注意不要一见sin x 就得出－1≤sin x ≤1，要根据x 的范围确定．3.设|x |≤π4，求函数f (x )＝cos 2x ＋sin x 的最小值．[解] f (x )＝cos 2x ＋sin x ＝1－sin 2x ＋sin x ＝－⎝ ⎛⎭⎪⎫sin x －122＋54.∵|x |≤π4，∴－22≤sin x ≤22，∴当sin x ＝－22时取最小值为1－22.正弦函数的图像答下列问题：(1)观察函数图像，写出满足下列条件的x 的区间． ①y >1；②y <1.(2)若直线y ＝a 与y ＝1－2sin x 有两个交点，求a 的取值范围； (3)求函数y ＝1－2sin x 的最大值，最小值及相应的自变量的值． [解] 按五个关键点列表：x －π －π2 0 π2 π sin x 0 －1 0 1 0 y ＝1－131－112sin x描点连线得：(1)由图像可知图像在y＝1上方部分y>1，在y＝1下方部分y<1，∴当x∈(－π，0)时，y>1，当x∈(0，π)时，y<1.(2)如图，当直线y＝a与y＝1－2sin x有两个交点时，1<a<3或－1<a<1，∴a 的取值范围是{a|1<a<3或－1<a<1}．(3)由图像可知y最大值为3，此时x＝－π2；y最小值为－1，此时x＝π2.1.解答本题的关键是要抓住五个关键点，使函数中x取－π，－π2，0，π2，π，然后相应求出y值，作出图像．2.“五点法”作图是画三角函数的简图的常用方法，这五点主要指函数的零点及最大值、最小值点，连线要保持光滑，注意凸凹方向．3.仔细观察图像，找出函数图像y＝1与y＝a的交点及最大值，最小值点正确解答问题．4．用“五点法”画出函数y＝12＋sin x，x∈[0,2π]上的图像．[解]取值列表如下：x 0π2π3π22πsin x 010－10y＝12＋sin x 123212－1212描点，并将它们用光滑的曲线连接起来．(如图)1.正弦函数周期性的释疑由正弦函数的图像和周期函数的定义可得：正弦函数是周期函数，2kπ(k∈Z 且k≠0)都是它的周期，最小正周期为2π.2.正弦函数的奇偶性(1)正弦函数是奇函数，反映在图像上，正弦曲线关于原点O对称．(2)正弦曲线既是中心对称图形又是轴对称图形．3.正弦函数单调性的说明(1)正弦函数在定义域R上不是单调函数，但存在单调区间．(2)求解(或判断)正弦函数的单调区间(或单调性)是求值域(或最值)的关键一步．(3)确定含有正弦函数的较复杂的函数单调性时，要注意使用复合函数的判断方法来判断．4．正弦函数最值的释疑(1)明确正弦函数的有界性，即|sin x|≤1.(2)对有些正弦函数，其最值不一定是1或－1，要依赖函数定义域来决定．(3)形如y＝A sin(ωx＋φ)(A>0，ω>0)的函数的最值通常利用“整体代换”，即令ωx＋φ＝z，将函数转化为y＝A sin z的形式求最值．5．“五点法”画正弦函数图像“五点法”是画三角函数图像的基本方法，在要求精度不高的情况下常用此法．1.以下对于正弦函数y＝sin x的图像描述不正确的是()A ．在x ∈[2k π，2k π＋2π]，k ∈Z 上的图像形状相同，只是位置不同B ．关于x 轴对称C ．介于直线y ＝1和y ＝－1之间D ．与y 轴仅有一个交点B [观察y ＝sin x 图像可知A ，C ，D 项正确，且关于原点中心对称，故选B ．]2.函数y ＝－sin x ，x ∈⎣⎢⎡⎦⎥⎤－π2，3π2的简图是( )D [可以用特殊点来验证．当x ＝0时，y ＝－sin 0＝0，排除A ，C ；当x ＝3π2时，y ＝－sin 3π2＝1，排除B ．]3.若sin x ＝2m ＋1且x ∈R ，则m 的取值范围是________． [－1,0] [因为－1≤sin x ≤1，sin x ＝2m ＋1， 所以－1≤2m ＋1≤1， 解得－1≤m ≤0.]4．用五点法画出函数y ＝－2sin x 在区间[0,2π]上的简图． [解] 列表：x 0 π2 π 3π2 2π sin x1－1y＝－2sin x 0－202011/11。

正弦函数、余弦函数的图像(附答案)正弦函数、余弦函数的图象[学习目标]“五点法”画正弦曲线和余弦曲线的步骤和方法，能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系．知识点一正弦曲线正弦函数y＝sin x(x∈R)的图象叫正弦曲线．利用几何法作正弦函数y＝sin x，x∈[0,2π]的图象的过程如下：①作直角坐标系，并在直角坐标系y轴的左侧画单位圆，如图所示．②把单位圆分成12等份(等份越多，画出的图象越精确)．过单位圆上的各分点作x轴的垂线，可以得到对应于0，π6，π3，π2，…，2π等角的正弦线．③找横坐标：把x 轴上从0到2π(2π≈6.28)这一段分成12等份．④平移：把角x 的正弦线向右平移，使它的起点与x 轴上的点x 重合．⑤连线：用光滑的曲线将这些正弦线的终点依次从左到右连接起来，即得y ＝sin x ，x ∈[0,2π]的图象．在精度要求不太高时，y ＝sin x ，x ∈[0,2π]可以通过找出(0,0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0)五个关键点，再用光滑曲线将它们连接起来，就可得正弦函数的简图．思考 在所给的坐标系中如何画出y ＝sin x ，x∈[0,2π]的图象？如何得到y ＝sin x ，x ∈R 的图象？答案 y ＝sin x ，x ∈[0,2π]的图象(借助五点法得)如下：只要将函数y ＝sin x ，x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度)，就可以得到正弦函数y ＝sin x ，x ∈R 的图象．知识点二 余弦曲线余弦函数y ＝cos x (x ∈R)的图象叫余弦曲线． 根据诱导公式sin ⎝⎛⎭⎪⎪⎫x ＋π2＝cos x ，x ∈R.只需把正弦函数y ＝sin x ，x ∈R 的图象向左平移π2个单位长度即可得到余弦函数图象(如图)．要画出y ＝cos x ，x ∈[0,2π]的图象，可以通过描出(0,1)，⎝⎛⎭⎪⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎪⎫32π，0，(2π，1)五个关键点，再用光滑曲线将它们连接起来，就可以得到余弦函数y ＝cos x ，x ∈[0,2π]的图象． 思考 在下面所给的坐标系中如何画出y ＝cos x ，x ∈[0,2π]的图象？答案题型一“五点法”作图的应用例1利用“五点法”作出函数y＝1－sin x(0≤x≤2π)的简图．解(1)取值列表：x 0π2π3π22πsin x 010－11－sin x1012 1 (2)描点连线，如图所示：跟踪训练1作函数y＝sin x，x∈[0,2π]与函数y ＝－1＋sin x，x∈[0,2π]的简图，并研究它们之间的关系．解按五个关键点列表：x 0π2π3π22πsin x 010－1－1＋sin x－1－1－2－1利用正弦函数的性质描点作图：由图象可以发现，把y＝sin x，x∈[0,2π]的图象向下平移1个单位长度即可得y＝－1＋sin x，x ∈[0,2π]的图象．题型二 利用正弦、余弦函数图象求定义域 例2 求函数f (x )＝lg sin x ＋16－x 2的定义域．解 由题意得，x 满足不等式组⎩⎨⎧sin x >0，16－x 2≥0， 即⎩⎨⎧－4≤x ≤4，sin x >0，作出y ＝sin x 的图象，如图所示．结合图象可得定义域：x ∈[－4，－π)∪(0，π)．跟踪训练2 求函数f (x )＝lg cos x ＋25－x 2的定义域．解 由题意得，x 满足不等式组⎩⎨⎧cos x >025－x 2≥0， 即⎩⎨⎧cos x >0－5≤x ≤5，作出y ＝cos x 的图象，如图所示．结合图象可得定义域： x ∈⎣⎢⎢⎡⎭⎪⎪⎫－5，－32π∪⎝⎛⎭⎪⎪⎫－π2，π2∪⎝⎛⎦⎥⎥⎤32π，5.题型三 利用正弦、余弦函数图象判断零点个数 例3 在同一坐标系中，作函数y ＝sin x 和y ＝lg x 的图象，根据图象判断出方程sin x ＝lg x 的解的个数．解建立坐标系xOy，先用五点法画出函数y＝sin x，x∈[0,2π]的图象，再依次向左、右连续平移2π个单位，得到y＝sin x的图象．描出点(1,0)，(10,1)并用光滑曲线连接得到y＝lg x的图象，如图所示．由图象可知方程sin x＝lg x的解有3个．跟踪训练3方程x2－cos x＝0的实数解的个数是．答案 2解析作函数y＝cos x与y＝x2的图象，如图所示，由图象，可知原方程有两个实数解．数形结合思想在三角函数中的应用例4 函数f (x )＝sin x ＋2|sin x |，x ∈[0,2π]的图象与直线y ＝k 有且仅有两个不同的交点，求k 的取值范围． 解f (x )＝sinx ＋2|sinx |＝⎩⎨⎧3sin x ，x ∈[0，π]，－sin x ，x ∈π，2π].图象如图，若使f (x )的图象与直线y ＝k 有且仅有两个不同的交点，根据图可得k 的取值范围是(1,3)．1．函数y ＝sin x (x ∈R)图象的一条对称轴是( ) A ．x 轴 B ．y 轴 C ．直线y ＝xD ．直线x ＝π22．用五点法画y ＝sin x ，x ∈[0,2π]的图象时，下列哪个点不是关键点( ) A ．(π6，12)B ．(π2，1)C ．(π，0)D ．(2π，0)3．函数y ＝sin x ，x ∈[0,2π]的图象与直线y ＝－12的交点为A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝ .4．利用“五点法”画出函数y ＝2－sin x ，x ∈[0,2π]的简图．5．已知0≤x≤2π，试探索sin x与cos x的大小关系．一、选择题1．函数y ＝－sin x ，x ∈⎣⎢⎢⎡⎦⎥⎥⎤－π2，3π2的简图是( )2．在同一平面直角坐标系内，函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象( ) A ．重合B ．形状相同，位置不同C ．关于y 轴对称D ．形状不同，位置不同3．方程sin x ＝x10的根的个数是( )A ．7B ．8C ．9D ．104．函数y ＝cos x ＋|cos x |，x ∈[0,2π]的大致图象为( )5．如图所示，函数y ＝cos x |tan x |(0≤x <3π2且x ≠π2)的图象是( )6．若函数y ＝2cos x (0≤x ≤2π)的图象和直线y ＝2围成一个封闭的平面图形，则这个封闭图形的面积是( )A ．4B ．8C ．2πD ．4π 二、填空题 7．函数y ＝log 12sin x 的定义域是 ．8．函数y ＝2cos x ＋1的定义域是 ． 9．函数f (x )＝sin x ＋116－x2的定义域为 ．10．设0≤x≤2π，且|cos x－sin x|＝sin x－cos x，则x的取值范围为．三、解答题11．用“五点法”画出函数y＝12＋sin x，x∈[0,2π]的简图．12．根据y＝cos x的图象解不等式：－32≤cos x≤12，x∈[0,2π]．13．分别作出下列函数的图象． (1)y ＝|sin x |，x ∈R ； (2)y ＝sin|x |，x ∈R.当堂检测答案1．答案 D 2．答案 A 3．答案 3π 解析 如图所示， x 1＋x 2＝2×3π2＝3π.4．解 (1)取值列表如下：x0 π2 π 3π22πsin x 010－1y＝2－sin x2123 2(2)描点连线，图象如图所示：5．解用“五点法”作出y＝sin x，y＝cos x(0≤x≤2π)的简图．由图象可知①当x＝π4或x＝5π4时，sin x＝cos x；②当π4<x<5π4时，sin x>cos x；③当0≤x <π4或5π4<x ≤2π时，sin x <cos x .课时精炼答案一、选择题 1．答案 D 2．答案 B解析 根据正弦曲线的作法可知函数y ＝sin x ，x ∈[0,2π]与y ＝sin x ，x ∈[2π，4π]的图象只是位置不同，形状相同． 3．答案 A解析 在同一坐标系内画出y ＝x10和y ＝sin x 的图象如图所示：根据图象可知方程有7个根．4．答案 D 解析 由题意得y ＝⎩⎪⎨⎪⎧2cos x ，0≤x ≤π2或32π≤x ≤2π，0，π2<x <32π.显然只有D 合适．5．答案 C解析 当0≤x <π2时，y ＝cos x ·|tan x |＝sin x ；当π2<x ≤π时，y ＝cos x ·|tan x |＝－sin x ； 当π<x <3π2时，y ＝cos x ·|tan x |＝sin x ，故其图象为C.6．答案 D解析 作出函数y ＝2cos x ，x ∈[0,2π]的图象，函数y ＝2cos x ，x ∈[0,2π]的图象与直线y ＝2围成的平面图形为如图所示的阴影部分．利用图象的对称性可知该阴影部分的面积等于矩形OABC 的面积，又∵OA ＝2，OC ＝2π， ∴S 阴影部分＝S 矩形OABC ＝2×2π＝4π. 二、填空题7．答案 {x |2k π<x <2k π＋π，k ∈Z}解析 由log 12sin x ≥0知0<sin x ≤1，由正弦函数图象知2k π<x <2k π＋π，k ∈Z. 8．答案 ⎣⎢⎢⎡⎦⎥⎥⎤2k π－23π，2k π＋23π，k ∈Z解析 2cos x ＋1≥0，cos x ≥－12，结合图象知x ∈⎣⎢⎢⎡⎦⎥⎥⎤2k π－23π，2k π＋23π，k ∈Z. 9．答案 (－4，－π]∪[0，π]解析 ⎩⎨⎧ sin x ≥0，16－x 2>0⇒⎩⎨⎧2k π≤x ≤2k π＋π，－4<x <4⇒－4<x ≤－π或0≤x ≤π. 10．答案 ⎣⎢⎢⎡⎦⎥⎥⎤π4，5π4解析 由题意知sin x －cos x ≥0，即cos x ≤sin x ，在同一坐标系画出y ＝sin x ，x ∈[0,2π]与y ＝cos x ，x ∈[0,2π]的图象，如图所示：观察图象知x ∈⎣⎢⎢⎡⎦⎥⎥⎤π4，5π4.三、解答题11．解 (1)取值列表如下：x 0π2π32π2πsin x 010－112＋sin x123212－1212(2)描点、连线，如图所示．12．解函数y＝cos x，x∈[0,2π]的图象如图所示：根据图象可得不等式的解集为{x |π3≤x ≤5π6或7π6≤x ≤5π3}． 13．解(1)y＝|sinx |＝⎩⎨⎧sin x (2k π≤x ≤2k π＋π)，－sin x (2k π＋π<x ≤2k π＋2π)(k ∈Z)．其图象如图所示，(2)y ＝sin|x |＝⎩⎨⎧sin x (x ≥0)，－sin x (x <0).其图象如图所示，。

高三数学三角函数图象变换试题答案及解析1.将函数图象上各点的横坐标伸长到原来的2倍，再向左平移个单位，纵坐标不变，所得函数图象的一条对称轴的方程是A．B．C．D．【答案】A【解析】由已知，横坐标伸长到原来的2倍，则x变为2x，，向左平移个单位，x变为，，即，对称轴，化简得，当k取1时，故选：A．【考点】三角函数的图象变换．2.若把函数的图象向右平移m个单位（m＞0）后，所得到的图象关于轴对称，则m的最小值是（）A．B．C．D．【答案】D【解析】，图象向右平移m个单位（m＞0）后，得到，其图象关于轴对称，即是偶函数，所以，解得m的最小值是，选D.【考点】三角函数辅助角公式，三角函数图象的变换.3.将函数图象所有的点向右移动个单位长度，再将所得各点的横坐标缩短到原来的倍（纵坐标不变），所得图象的函数解析式为（）A．B．C．D．【答案】C【解析】将函数图象所有的点向右移动个单位长度后所得图象的函数解析式为，再将所得各点的横坐标缩短到原来的倍（纵坐标不变），所得图象的函数解析式为.故C正确.【考点】三角函数的伸缩平移变换.4.已知函数y=cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则()A．ω=1,φ=B．ω=1,φ=-C．ω=2,φ=D．ω=2,φ=-【答案】D【解析】因为=-=,所以T=π,所以ω=2,又×2+φ=,所以φ=-.5.将函数的图像向右平移个单位，再将图像上每一点横坐标缩短到原来的倍，所得图像关于直线对称，则的最小正值为．【答案】【解析】由题意得：函数变为，因为所得图像关于直线对称，所以的最小正值为.【考点】三角函数图像变换6.函数的图像与轴的交点的横坐标构成一个公差为的等差数列，要得到函数的图像只需将的图像（）A．向左平移B．向右平移C．向左平移D．向右平移【答案】A【解析】由题意知函数的周期为，即；将向右平移个单位，得到.【考点】三角函数的图像平移变换.7.要得到函数的图象，只需将函数的图象上所有的点（）A．横坐标缩短到原来的倍（纵坐标不变）,再向左平行移动个单位长度B．横坐标缩短到原来的倍（纵坐标不变），再向右平行移动个单位长度C．横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动个单位长度D．横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动个单位长度【答案】C【解析】将函数的图象上所有的点横坐标伸长到原来的2倍（纵坐标不变），得到，然后向左平移个单位得到函数，选C.8.把函数y＝cos2x＋1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是【答案】B【解析】把函数的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得：，向左平移1个单位长度得：，再向下平移1个单位长度得：．令x＝0，得：；x＝，得：；观察即得答案．9.将函数的图象向右平移个单位，再向上平移1个单位后得到的函数对应的表达式为，则函数的表达式可以是A．B．C．D．【答案】D【解析】由题意，选D．【考点】图象变换．10.函数的图像经过下列平移，可以得到偶函数图像的是（）A．向右平移个单位B．向左平移个单位C．向右平移个单位D．向左平移个单位【答案】C【解析】由题意，假设向左平移个单位得到偶函数，即为偶函数，则，解得，由选项可知，当时，，即向右平移个单位，故选C.【考点】1.三角函数的平移；2.三角函数的奇偶性.11.将函数的图象向右平移个单位，再向上平移1个单位，所得函数图象对应的解析式为 ( )A．B．C．D．【答案】C【解析】将函数的图象向右平移个单位，得到，再向上平移1个单位，得到，故选C.【考点】三角函数图象变换12.已知函数的图象经过点.（1）求实数的值；（2）设，求函数的最小正周期与单调递增区间.【答案】（1）；（2）最小正周期为，单调递增区间为.【解析】（1）将点代入函数的解析式即可求出实数的值；（2）根据（1）中的结果，先将函数的解析式进行化简，化简为或，再根据周期公式计算函数的最小正周期，再利用整体法对施加相应的限制条件，解出的取值范围，即可求出函数的单调递增区间.试题解析：（1）由于函数的图象经过点，因此，解得，所以；（2），因此函数的最小正周期，由，解得，故函数的单调递增区间为.【考点】1.二倍角公式；2.三角函数的周期性与单调性13.若ω>0，函数y＝cosωx＋的图像向右平移个单位长度后与原图像重合，则ω的最小值为()A．B．C．3D．4【答案】C【解析】由题意，得＝k (k∈N*)，所以ω＝3k(k∈N*)，所以ω的最小值为3.14.将函数y＝cos x＋sin x(x∈R) 的图象向左平移m(m＞0)个单位长度后，所得到的图象关于y轴对称，则m的最小值是________．【答案】【解析】y＝cos x＋sin x＝2sin ，向左平移m个单位长度后得到y＝2sin ，由它关于y轴对称可得sin(＋m)＝±1，∴＋m＝kπ＋，k∈Z，∴m＝kπ＋，k∈Z又m>0，∴m的最小值为.15.为了得到函数y＝sin 的图象，只需把函数y＝sin 的图象()．A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度【答案】B【解析】注意到把y＝sin 的图象向右平移个单位长度得到y＝sin [2(x－)＋]＝sin 的图象，故选B.16.函数f(x)＝A sin (ωx＋φ)(其中A>0，|φ|<)的图象如图所示，为了得到g(x)＝sin 3x的图象，只需将f(x)的图象()．A．向右平移个单位长度B．向左平移个单位长度C．向右平移个单位长度D．向左平移个单位长度【答案】C【解析】由图象可知A＝1，，即T＝＝，所以ω＝3，所以f(x)＝sin (3x＋φ)，又f＝sin ＝sin ＝－1，所以＋φ＝＋2kπ，k∈Z，即φ＝＋2kπ，k∈Z，又|φ|<所以φ＝，即f(x)＝sin，又g(x)＝sin 3x＝sin＝sin ，所以只需将f(x)的图象向右平移个单位长度，即可得到g(x)＝sin 3x的图象．17.已知的图像与的图像的两个相邻交点间的距离为，要得到的图像，只须把的图像 ( )A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【答案】A【解析】由于函数的最大值为1，又函数的图像与的图像的两个相邻交点间的距离为，所以函数的周期为.所以.所以函数的解析式为.所以要得到函数只需要将向左平移各单位即可.故选A.【考点】1.三角函数的图像.2.三角函数图像的平移.3.三函数的诱导公式.18.定义＝a1a4－a2a3,若函数f(x)＝，则将f(x)的图象向右平移个单位所得曲线的一条对称轴的方程是()．A．x＝B．x＝C．x＝D．x＝π【答案】A【解析】由定义可知，f(x)＝sin 2x－cos 2x＝2sin，将f(x)的图象向右平移个单位得到y＝2sin ＝2sin，由2x－＝＋kπ，k∈Z.得对称轴为x＝，k∈Z，当k＝－1时，对称轴为x＝.19.将函数的图像分别向左、右平移个单位，所得的图像关于y轴对称，则的最小值分别是（）A．B．C．D．【答案】A【解析】因为将函数的图像向左平移个单位可得函数为.其图像关于y轴对称，则.所以所以最小的.同理可求出向右平移个单位的图像关于y轴对称的的最小值为.故选A.【考点】1.三角函数的左右平移.2.三角函数的奇偶性.3.待定系数方程的解法.20.要得到函数的图象，只要将函数的图象（）A．向左平移2个单位B．向右平移2个单位C．向左平移个单位D．向右平移个单位【答案】D【解析】因为，所以，要得到函数的图象，只要将函数的图象向右平移个单位，选D.【考点】三角函数图象的平移21.为了得到函数的图象，可以将函数的图象( )A．向右平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向左平移个单位长度【答案】B【解析】因为.又因为余弦函数是偶函数.所以.所以为了得到函数的图象可以由函数的图象右平移的单位.即选B.【考点】1.正弦函数与余弦函数的相互转化.2.三角函数的平移问题.22.函数的部分图像如图，其中,且，则f(x)在下列哪个区间中是单调的（）A．B．C．D．【答案】B【解析】当图像过原点时，即时，，在上为减函数，上为增函数当图像的最高点在轴上时，，在上是减函数，上为增函数，所以在上是单调的.【考点】1.三角函数的单调区间；2.三角函数图像.23.函数（其中＞0，＜的图象如图所示，为了得到的图象，只需将的图象A．向右平移个单位长度B．向左平移个单位长度C．向左平移个单位长度D．向右平移个单位长度【答案】D【解析】A=1，，即T=，所以3，由得，所以=sin （3x+）=，所以把函数的图象向右平移个单位长度得到函数的图象，故选D.【考点】1.正弦型函数的性质和图像；2.函数图像的变换规律.24.如果函数的图像关于直线对称，则（）A．B．C．D．【答案】D【解析】由的图像关于直线对称，则在处取得最值，所以，而，所以，故选D.【考点】1.三角函数的性质；2.函数的最值求解.25.要得到一个奇函数，只需将的图象（）A．向右平移个单位B．向右平移个单位C．向左平移个单位D．向左平移个单位【答案】C【解析】，因为是奇函数，所以将的图象向左平移个单位，得到的图象，故答案为：向左平移个单位．【考点】三角函数图像变化，两角和与差的正弦，三角函数的奇偶性．26.将函数y＝f(x)·sinx的图象向右平移个单位后，再作关于x轴的对称变换，得到函数y＝1－2sin2x的图象，则f(x)可以是 ()．A．sinx B．cosx C．2sinx D．2cosx【答案】D【解析】将函数y＝f(x)·sin x的图象向右平移个单位得,再作关于x轴的对称变换得，，即，令则，所以，，故f(x)可以是2cos x，选D.【考点】三角函数图象平移变换、二倍角公式.27.将函数的图象向右平移个单位长度得到图象,若的一个对称中心是，则的一个可能取值是( )A．B．C．D．【答案】【解析】将函数的图象向右平移个单位长度，所得到图象的解析式为：.因为的一个对称中心是，所以，即.取得.【考点】三角函数图象的变换.28.设,函数图像向右平移个单位与原图像重合，则最小值是（）A．B．C．D．3【答案】C【解析】图像向右平移个单位，得到，与图像重合，∴，∴，∴.【考点】1.图像的平移变换；2.三角函数的图像.29.为了得到函数的图象，只需把函数的图象（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位【答案】B【解析】∵，∴只需把函数的图象向右平移个单位，选B.【考点】三角函数的图象.30.将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），再将所得的图象向左平移个单位，得到的图象对应的解析式是（）A．B．C．D．【答案】C【解析】，故选C.【考点】三角函数图象变换31.已知函数，且当时，的最小值为2.（1）求的值，并求的单调增区间；（2）将函数的图象上各点的纵坐标保持不变，横坐标缩短到原来的倍，再把所得图象向右平移个单位，得到函数，求方程在区间上的所有根之和.【答案】（1）0，；（2）.【解析】（1）首先利用三角函数的和差倍半公式，将原三角函数式化简，根据三角函数的性质，确定得到最小值的表达式，求得；（2）遵循三角函数图象的变换规则，得到，利用特殊角的三角函数值，解出方程在区间上的所有根，求和.试题解析：（1） 2分因为，时，的最小值为2，所以，. 4分6分（2） 9分由，. 11分12分【考点】三角函数的和差倍半公式，三角函数图象的变换.32.函数的最小正周期为，为了得到函数的图象，只要将的图象（）.A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度【答案】A【解析】由T=,所以=2，因为，故选A.【考点】正弦型函数的性质和图象的平移.33.将函数的图像向右平移个单位，那么所得的图像所对应的函数解析式是（）A．B．C．D．【答案】D.【解析】由已知得平移后的图像所对应的函数解析式是，故选【考点】三角函数图像变换.34.已知的图象与的图象的两相邻交点间的距离为，要得到的图象，只须把的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【答案】C【解析】，，由于函数的图象与的图象的两相邻交点的距离为，即函数的最小正周期为，，，故得到函数的图象，只需将函数的图象向左平移个单位.【考点】辅助角变换、三角函数周期、三角函数图象变换35.将函数的图像向左平移个单位，得到的图像，则的解析式为 () A．B．C．D．【答案】A【解析】将图像向左平移个单位，得到.【考点】三角函数图像的平移.36.函数的图像向右平移个单位后，与函数的图像重合，则=___________.【答案】【解析】因为原函数解析式为，所以图象平移后的解析式为=，所以，解得.【考点】本小题主要考查诱导公式、三角函数的图象变换等基础知识，这两部分知识都是高考的热点内容之一，几乎年年必考，熟练其基础知识是解答好本类题目的关键.37.将函数的图形按向量平移后得到函数的图形，满足，则向量的一个可能值是（）A．B．C．D．【答案】B【解析】，则关于直线对称，则是奇函数，图像关于对称，，函数变形为，将其向右平移向上平移3个单位可得对称中心在原点，平移向量为【考点】三角函数平移变换点评：在三角函数中，x轴方向的平移与有关，伸缩与有关，Y轴方向的平移与有关，伸缩与有关38.设的最大值为16，则。

1．4三角函数的图象与性质第9课时正弦函数、余弦函数的图象答案B解析由y＝sin x，x∈[0，2π]的图象，作出y＝－sin x，x∈[0，2π]的图象，再画出y＝1－sin x，x∈[0，2π]的图象．A．只关于x轴对称B．关于原点对称C．关于原点、x轴对称D．关于原点、坐标轴对称答案C解析作出函数y＝cos x与函数y＝－cos x的简图(图略)，易知选C．3．函数y＝cos x＋|cos x|，x∈[0，2π]的大致图象为()答案D解析 由题意得y ＝⎩⎪⎨⎪⎧2cos x ，0≤x ≤π2或3π2≤x ≤2π，0，π2<x <3π2.4．函数y ＝－cos x (x >0)的图象中与y 轴距离最近的最高点的坐标为( ) A ．π2，1 B ．(π，1) C ．(0，1) D ．(2π，1) 答案 B解析 作出函数y ＝－cos x (x >0)的图象，如图所示，由图易知与y 轴距离最近的最高点的坐标为(π，1)．A ．π4，3π4B ．π4，π2∪5π4，3π2C ．π4，π2D ．5π4，7π4 答案 A解析 ∵sin x >|cos x |，∴sin x >0，∴x ∈(0，π)，在同一坐标系中画出y ＝sin x ，x ∈(0，π)与y ＝|cos x |，x ∈(0，π)的图象，观察图象易得x ∈π4，3π4．6．用“五点法”作出函数y ＝1－2sin x ，x ∈[－π，π]的简图，并回答下列问题：(1)观察函数图象，写出满足下列条件的x的区间．①y>1，②y<1；(2)若直线y＝a与y＝1－2sin x，x∈[－π，π]的图象有两个交点，求a的取值范围．解列表如下：描点并将它们用光滑的曲线连接起来，如图．(1)由图象可知图象在直线y＝1上方部分时y>1，在直线y＝1下方部位时y<1，所以①当x∈(－π，0)时，y>1；②当x∈(0，π)时，y<1．(2)如图所示，当直线y＝a与y＝1－2sin x，x∈[－π，π]的图象有两个交点时，1<a<3或－1<a<1，所以a的取值范围是(－1，1)∪(1，3)．7．方程sin x＝1－a2在x∈π3，π上有两个实数根，求a的取值范围．解首先作出y＝sin x，x∈π3，π的图象，然后再作出y＝1－a2的图象，如果y ＝sin x ，x ∈π3，π与y ＝1－a 2的图象有两个交点，方程sin x ＝1－a 2，x ∈π3，π就有两个实数根．设y 1＝sin x ，x ∈π3，π，y 2＝1－a 2． y 1＝sin x ，x ∈π3，π的图象如图．由图象可知，当32≤1－a 2<1，即－1<a ≤1－3时，y ＝sin x ，x ∈π3，π的图象与y ＝1－a 2的图象有两个交点，即方程sin x ＝1－a 2在x ∈π3，π上有两个实根，所以a 的取值范围为－1<a ≤1－3．一、选择题1．若sin θ＝1－log 2x ，则实数x 的取值范围是( ) A ．[1，4] B ．14，1 C ．[2，4] D ．14，4 答案 A解析 由正弦函数的图象，可知－1≤sin θ≤1，所以－1≤1－log 2x ≤1，整理得0≤log 2x ≤2，解得1≤x ≤4，故选A ．2．要得到函数y ＝－sin x 的图象，只需将函数y ＝cos x 的图象( ) A ．向右平移π2个单位长度 B ．向右平移π个单位长度 C ．向左平移π2个单位长度 D ．向左平移π个单位长度 答案 C解析 因为y ＝cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，由图象平移变换可知，由y ＝cos x 图象向左平移π2个单位即可得到y ＝－sin x 的图象，故选C ．3．在[0，2π]上，满足sin x ≥32的x 的取值范围是( ) A ．⎣⎢⎡⎦⎥⎤0，π3 B ．⎣⎢⎡⎦⎥⎤π3，5π3C ．⎣⎢⎡⎦⎥⎤π3，2π3D ．⎣⎢⎡⎦⎥⎤5π6，π答案 C解析 y ＝32与y ＝sin x 的两个交点为π3，32，2π3，32，∴x 的取值范围为⎣⎢⎡⎦⎥⎤π3，2π3．4．方程sin x ＝lg x 的解有( ) A ．1个 B ．2个 C ．3个 D ．4个 答案 C解析 如图所示，由于y ＝lg x 的图象过点(10，1)，故两图象有3个公共点，所以方程sin x ＝lg x 有3个解．5．函数y ＝1＋sin x ，x ∈[0，2π]的图象与直线y ＝2交点的个数是( ) A ．0 B ．1 C ．2 D ．3 答案 B解析 由函数y ＝1＋sin x ，x ∈[0，2π]的图象(如图所示)，可知其与直线y ＝2只有1个交点．二、填空题6．关于三角函数的图象，有下列命题：①y ＝sin|x |与y ＝sin x 的图象关于y 轴对称； ②y ＝cos(－x )与y ＝cos|x |的图象相同； ③y ＝|sin x |与y ＝sin(－x )的图象关于x 轴对称； ④y ＝cos x 与y ＝cos(－x )的图象关于y 轴对称． 其中真命题是________．(写出所有真命题的序号) 答案 ②④解析 对于②，y ＝cos(－x )＝cos x ，y ＝cos|x |＝cos x ，故其图象相同；对于④，y ＝cos(－x )＝cos x ，故其图象关于y 轴对称；由图可知①③均不正确．故真命题是②④．7．函数y ＝cos x ＋4，x ∈[0，2π]的图象与直线y ＝4的交点坐标为________． 答案 ⎝ ⎛⎭⎪⎫π2，4，⎝ ⎛⎭⎪⎫3π2，4解析 作出函数y ＝cos x ＋4，x ∈[0，2π]的图象(图略)，容易发现它与直线y ＝4的交点坐标为⎝ ⎛⎭⎪⎫π2，4，⎝ ⎛⎭⎪⎫3π2，4．8．已知函数f (x )＝sin x ＋2|sin x |，x ∈[0，2π]的图象与直线y ＝k 有且仅有两个不同的交点，则k 的取值范围是________．答案 (1，3)解析 f (x )＝sin x ＋2|sin x |＝⎩⎨⎧3sin x ，x ∈[0，π]，－sin x ，x ∈(π，2π]的图象如图．若使f (x )的图象与直线y ＝k 有且仅有两个不同的交点，根据图象可得k 的取值范围是(1，3)．三、解答题9．分别作出下列函数的图象．(1)y ＝|cos x |，x ∈R ； (2)y ＝sin|x |，x ∈R ．解(1)y ＝|cos x |＝⎩⎪⎨⎪⎧cos x 2k π－π2≤x ≤2k π＋π2，－cos x 2k π＋π2<x <2k π＋3π2(k ∈Z )．其图象如图所示．(2)y ＝sin|x |＝⎩⎨⎧sin x (x ≥0)，－sin x (x <0)，其图象如图所示．10．已知0≤x ≤2π，试探索sin x 与cos x 的大小关系． 解 用“五点法”作出y ＝sin x ，y ＝cos x (0≤x ≤2π)的简图． 由图象可知，①当x ＝π4或x ＝5π4时，sin x ＝cos x ； ②当π4<x <5π4时，sin x >cos x ；③当0≤x <π4或5π4<x ≤2π时，sin x <cos x ．。

完整版)正余弦函数图象与性质练习题正弦函数和余弦函数是初中数学中常见的三角函数，它们的图像和性质也是高中数学中必须掌握的内容。

一、选择题1.函数 $y=2\sin(2x+\frac{\pi}{3})$ 的图像关于点（$-\frac{\pi}{6}$，0）对称。

2.函数 $y=2\sin(\frac{\pi}{6}-2x)$ 在区间$[\frac{\pi}{12},\frac{\pi}{2}]$ 上是增函数。

3.设 $a$ 为常数，且 $a>1$，$-\frac{\pi}{2}\leq x\leq 2\pi$，则函数 $f(x)=\cos 2x+2a\sin x-1$ 的最大值为 $2a+1$。

4.函数 $y=\sin(2x+\frac{5}{2}\pi)$ 的一个对称轴方程是$x=\frac{5}{4}\pi$。

5.方程 $\cos(x+\frac{5}{2}\pi)=\frac{1}{2}x$ 在区间$(0,100\pi)$ 中有 $102$ 个解。

6.函数 $y=\sin(2x+\pi)$ 是以 $\pi$ 为周期的偶函数。

7.如果函数 $y=\sin 2x+\alpha\cos 2x$ 的图像关于直线$x=-\frac{\pi}{8}$ 对称，则 $\alpha=-2$。

8.函数 $y=2\cos 2x+1$ 的最小正周期为 $\pi$。

9.已知函数 $f(x)=\sin(\pi x-\frac{\pi}{2})-1$，则命题“$f(x)$ 是周期为 $2$ 的偶函数”是正确的。

10.函数 $y=-\cos x+\frac{\cos x}{\sin x}$ 的定义域为$(2k\pi+\pi,2k\pi+\frac{3}{2}\pi]$。

11.定义在 $\mathbb{R}$ 上的函数 $f(x)$ 既是偶函数又是周期函数，且最小正周期为 $\pi$，当$x\in[\frac{\pi}{2},\pi]$ 时，$f(x)=\sin x$，则$f(\frac{5\pi}{3})=-\frac{1}{2}$。

高二数学三角函数图象变换试题答案及解析1.将奇函数的图象向左平移个单位得到的图象关于原点对称，则的值可以为A．B．C．D．【答案】B【解析】由已知可知f（x）的图象过点，则即，答案选B.【考点】三角函数的图象与变换2.在同一坐标系中，将曲线变为曲线的伸缩变换是（）【答案】C【解析】将曲线y=2sin3x变为曲线y=sinx即y′=sinx′，横坐标变为原来的3倍，纵坐标变为原来的倍，将曲线y=2sin3x变为曲线y=sinx的伸缩变换是：，故选C．【考点】函数y=Asin（ωx+∅）的图象变换.3.为了得到函数的图像，只需把函数的图像（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位【答案】D【解析】三角函数的左右平移就是x的值的变化，相应y值的变化.所以要将函数中的x变为，就可得函数，所以图像是向右平移了个单位.即选D.【考点】三角函数图像的平移.4.要得到函数的导函数的图象，只需将的图象（）A．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）B．向左平移个单位，再把各点的纵坐标缩短到原来的倍（横坐标不变）C．向左平移个单位，再把各点的纵坐标伸长到原来的倍（横坐标不变）D．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）【答案】D【解析】根据题意，由于函数的导函数=2cos(2x+)的图象，那么可以将的图象向左平移个单位，得到2sin（(2（x+)+)，再把各点的纵坐标伸长到原来的2倍（横坐标不变）得到=2cos(2x+)，故答案为D.【考点】三角函数图象的变换点评：主要是考查了三角函数图象的变换，属于基础题。

5.要得到函数的导函数的图象，只需将的图象（）A．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）B．向左平移个单位，再把各点的纵坐标缩短到原来的倍（横坐标不变）C．向左平移个单位，再把各点的纵坐标伸长到原来的倍（横坐标不变）D．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）【答案】D【解析】根据题意，由于=，根据三角函数的变换规律可知只需将的图象向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）得到函数的导函数的图象，故选D【考点】三角函数的图像变换点评：本题主要考查函数y=Asin（ωx+∅）的图象变换，属于基础题．6.根据市气象站对春季某一天气温变化的数据统计显示，气温变化的分布可以用曲线拟合（，单位为小时,表示气温，单位为摄氏度，，），现已知这天气温为4至12摄氏度，并得知在凌晨1时整气温最低，下午13时整气温最高。

个单位 B.向右平移个单位个单位个单位）=sin［2（x，就能得到y=sin（2）的图象.）的图象向右平移，则所得图象的函数解））的图象向右平移个单位，得y=sin［2（x）+］，即，就得到函数y=sin2（2x），即）的振幅为，初期.）的对称轴为=k（k∈）的图象，只需将函数y=sin（2x+）的图象，横坐标保持不变)，x∈个单位长度，再把各点的横坐标缩短到原来的（纵坐标不变）个单位长度，再把各点的横坐标缩短到原来的（纵坐标不变）个单位长度，再把各点的横坐标伸长到原来的3倍（纵坐标不变）个单位长度，再把各点的横坐标伸长到原来的3倍（纵坐标不变）），x∈+),）的图象是（ ）=2为最大值.所以直线x=, B.,, D.,=2.排除A、B.x+满足sin(×1+)=1.×1+x→y=3sin（x x-x-，，作出该函数在一个周期内的草图；，当x=，求-），列出下表：（2）依题意，有∴30分钟训练(巩固类训练，可用于课后)1.已知函数y=Asin（ωx+φ）在同一周期内，当x=时，y=2；当x=最大=-2，那么函数的解析式为（ ）时，y最小A.y=2sin（2x+）B.y=2sin（2x-）C.y=2sin（2x+）D.y=2sin（2x-）解析：由x=时，y=2，知A=2，同一周期内，y取最大与最小值时x相差-最大=.∴=,T=π.∴ω==2.∴y=2sin（2x+φ），代入最大值坐标，得φ=.答案：A2.函数y=sin（2x+）的图象的一条对称轴方程为（ ）A.x=B.x=-C.x=-D.x=解析：依题意，令sin（2x+）=±1，则2x+=kπ+，从而x=kπ-π，k∈Z.显然k=1时，x=，符合题意.答案：C3.已知正弦函数在一个周期内的图象如图1-3-3所示，则它的表达式应为 …（ ）sin（2x+）+ B.y=sin（2x）+sin（2x+）+ D.y=sin（2x）+，周期T=）=sin（2x+，k∈-］ B.［，-≤2x≤x≤，））-个单位，得到的曲线与y=sin（x-）sin（x+）sin（x+）sin（2x）sinx的图象沿x轴向右平移s），再将此函数图象上点的纵坐标不变，横坐标缩短为原来的sin（2x），此即y=f（x）的解析式.，2k］（k∈个单位，得到函数y=sin（2x+）的图象，但sin；对于②，sin2x＞0，2x∈［2k］）=）而不是y=sin（2x+）.，x+++，，k∈.∴所求解析式为y=x+）.x+）］上的最大值是］上为增函数.），即2sin.）+2a+b，x∈［，≤x≤≤）≤·.（30（30+10）=20.x+x+。

正弦函数的性质与图像、余弦函数的图像与性质和正切函数 正弦函数的性质与图像[要点]1．正弦函数的图像(1)掌握正弦函数的图像的画法；(2)会熟练运用五点法画有关正弦函数的简图． 2．对于正弦函数x y sin =要掌握： (1)定义域为R ； (2)值域[-1，1]； (3)最小正周期π2； (4)单调增区间],22,22[ππππ+-k k 单调减区间]232,22[ππππ++k k ，Z k ∈； (5)是奇函数，图像关于原点对称.同时要求会求有关正弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题. [随堂练习]1．sin y x =，[0,2]x π∈的图像与2y =-的交点个数为〔 〕 A ．0B ．1C ．2D ．32．()f x 为奇函数，且在[,0]2π-上为减函数，则()f x 可以为〔 〕A ．()sin f x x =B ．()sin f x x =-C ．()1sin f x x =+D ．()1sin f x x =-3．函数y =的值域是〔 〕A ．1[0,]2B ．C ．D ． 4．下列不等式正确的是〔 〕A ．ππ74sin 75sin >B ．9sin()sin 77ππ-> C ．)6sin()75sin(ππ->-D ．sin()sin 37ππ->5．函数11sin ,2y x x =-∈R 的最大值为，当取得这个最大值时自变量x 的取值的集合是．6．已知02θπ≤<，则满足1sin 2θ≤的θ的范围为__________． 7．构造一个周期为2π，最小值为32-，在[0,]2π上是减函数的奇函数()f x = __ ．8．利用“五点法〞画出函数1sin 2y x =-在长度为一个周期的闭区间的简图．9．求函数2sin sin 1,[,]44y x x x ππ=-++∈-的值域．答案1．C 在同一坐标系内画出sin y x =，[0,2]x π∈的图像与2y =-的图像， 可以看出交点个数为2． 2．B 对于A ，在[,0]2π-上为增函数；C 、D 都既不是奇函数，也不是偶函数．3．D 知311sin 222x -≤-≤，又在根号下，则110sin 22x ≤-≤，则[0,2y ∈． 4．B 5243sin sin sin sin 7777ππππ=<=，92sin()sin sin()777πππ->=-，52sin()sin sin()sin 7766ππππ-=-<-=-，sin()0sin 37ππ-<<，则B 正确． 5．32{2,}2x x k k Z ππ=-∈当sin x 取到最小值1-时，y 取最大值32， 此时{2,}2x x k k Z ππ=-∈．6．5[0,][,2)66πππ⋃画出12y =与sin y x =在[0,2)x π∈上的图像，看图可得． 7．3sin 2x -可以判断()f x =3sin 2x -满足要求．8．解：列表：作图：9．解：由[,]44x ππ∈-222215sin sin 1(sin )24y x x x =-++=--+，当1sin 2x =，即6x π=时，y 取最大值，为54；当sin 2x =-，即4x π=-时，y 取最小值，为12．所以函数的值域为15[,]24．备选题1．函数412sin y x=-+-的最大值是〔 〕A ．35B ．25C ．3D ．5 1．C 12sin 3x ≤-≤，则44432sin x ≤≤-，则133y ≤≤，选C ． 2．已知函数5sin ,[,]22y x x ππ=∈的图像与直线1y =围成一个封闭的平面图形，则该封闭图形的面积为〔 〕 A ．2 B ．4 C ．2π D ．π2．C 如图，由对称性知12S S =，34S S =， 则封闭图形的面积与长为2π，宽为1的矩形的面积相等，则封闭图形的面积为2π．余弦函数的图像与性质 [要点]1．余弦函数的图像(1)掌握余弦函数的图像的画法；(2)会熟练运用五点法画有关余弦函数的简图． 2．对于余弦函数x y cos =要掌握：(1)定义域为R ； (2)值域[-1，1]； (3)最小正周期π2；(4)单调增区间],2,)12[(ππk k -单调减区间])12(,2[ππ+k k Z k ∈； (5)是偶函数，图像关于y 轴对称.同时要求会求有关余弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题. [随堂练习]1．12cos y x =-的值域为〔 〕A ．[1,3]-B ．[1,3]C ．[3,1]-D ．[3,1]--2．函数sin()2y x π=+〔x ∈R 〕〔 〕A ．是奇函数，且在[,]22ππ-上是增函数 B ．是偶函数，且在[,0]π-上是减函数 C ．是偶函数，且在[0,]π上是减函数D ．是奇函数，且在[,]22ππ-上是减函数 3．函数cos y x =-的图像的一条对称轴方程是〔 〕A ．2π-=xB ．4π-=xC ．8π=x D ．x π=4．把函数sin y x =-的图像经过平移可以得到cos y x =的图像，这个平移可以为〔 〕A ．向左平移2π个单位B ．向右平移2π个单位C ．向左平移π个单位D ．向右平移π个单位5．函数y =的定义域为___________________．6．函数12cos y x=+的值域为_______________．7．函数x x y cos sin -+=的定义域是____________________． 8．判断下列函数的奇偶性：〔1〕()cos f x x x x =-； 〔2〕1()sin cos lg1xf x x x x-=⋅+． 9．用五点法作出函数2cos y x =-，[0,2]x π∈的图像，并说明它和函数cos y x =，[0,2]x π∈的图像的关系．答案1．A 因为cos [1,1]x ∈-，则2cos [2,2]x -∈-，则12cos [1,3]x -∈-． 2．C sin()cos 2y x x π=+=，则它是偶函数，且在[0,]π上是减函数．3．D 画出图像可知直线x π=是cos y x =-的图像的一条对称轴． 4．B ∵sin()cos 2y x x π=--=，则把函数sin y x =-的图像向右平移2π个单位 可以得到cos y x =的图像．5．3{2,}4x x k k Z ππ≠±∈ 10x +≠，那么cos 2x ≠-，而cos 2x =-在一个周期[,)ππ-内的x 值为34π±，则定义域为3{2,}4x x k k Z ππ≠±∈．6．1[,1]3 因为1cos 1x -≤≤，则12cos 3x ≤+≤，知值域为1[,1]3．7．])12(,22[πππ++k k ，Z k ∈ 可得sin 0x ≥，cos 0x ≤，由正弦线与余弦线知，22k x k πππ≤≤+且32222k x k ππππ+≤≤+，其中k Z ∈，那么两者的交集 即为定义域，为])12(,22[πππ++k k ，Z k ∈． 8．解：〔1〕()()()cos()cos ()f x x x x x x x f x -=----=-+=-， 所以()f x 是奇函数．〔2〕知函数的定义域为(1,1)-．1()1()sin()cos()lgsin cos lg 1()1x xf x x x x x x x--+-=--⋅=-⋅+--111sin cos lg()sin cos lg ()11x xx x x x f x x x---=-⋅=⋅=++，所以()f x 是偶函数．9．解：在同一坐标系中作出2cos y x =-与cos y x =的图像．可以看出，将函数cos y x =，[0,2]x π∈的图像关于x 轴对称可以得到函数cos y x =-，[0,2]x π∈的图像，再将函数cos y x =-，[0,2]x π∈ 的图像向上平移2个单位即可得到函数2cos y x =-，[0,2]x π∈的图像． 备选题1．若函数()f x 是周期为π的奇函数，且[0,]2x π∈时，()cos f x x =，则7()3f π-=______． 1．12-771()(2)()()cos 333332f f f f ππππππ-=-+=-=-=-=-．2．在△ABC 中，2C π>，若函数()y f x =在[0,1]上为单调递减函数，则下列命题正确的是〔 〕A ．(cos )(cos )f A fB >B ．(sin )(sin )f A f B >C ．(sin )(cos )f A f B >D ．(sin )(cos )f A f B < 2．C 2C π>，则2A B π+<，则022A B ππ<<-<，则0sin sin()cos 12A B B π<<-=<，则(sin )(cos )f A f B >．正切函数 [要点]1．正切函数的定义：αααcos sin tan =〔Z k k R ∈+≠∈,2,ππαα〕. 2．正切函数的图像：掌握正切函数的图像的画法.3．对于正切函数x y tan =要掌握： (1)定义域为},2,{Z k k x R x ∈+≠∈ππ；(2)值域R ；(3)周期是)0,(≠∈k Z k k π，最小正周期π； (4)在每一个开区间)2,2(ππππk k ++-)(Z k ∈是增加的Z k ∈；(5)是奇函数，图像关于原点对称.同时要求会求有关余弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题.4．正切函数的诱导公式，可结合正弦函数与余弦函数的诱导公式的记忆方法去记忆． [随堂练习]1．已知角α的终边经过点(1,2)P -，那么tan α等于〔 〕A ．2B ．2-C ．12 D ．12- 2．若点(tan sin ,sin )P ααα-在第三象限，则角α的终边必在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知1tan()2πα-=，则3tan()2πα+等于〔 〕 A ．2 B ．2-C ．12 D ．12-4．tan y x =图像的一个对称中心为〔 〕A ．(,0)2πB ．(,0)4πC ．(1,0)D ．(0,)π 5．00tan 300cot(405)+-=．6．比较13tan()4π-与17tan()5π-的大小为13tan()4π-17tan()5π-．7．函数y =的定义域为．8．求函数)32tan(π+=x y 的定义域和单调区间．9．求函数2tan 2tan 5y x a x =+⋅+在[,)42x ππ∈时的值域(其中a 为常数)． 答案1．B 可得2tan 21y x α-===-． 2．D 知sin 0α<，且tan sin 0αα-<，则tan sin 0αα<<，则α为第四象限角．3．A 1tan()2πα-=，则1tan 2α=-，则3tan()tan()cot 22ππααα+=+=-12tan α=-=．4．A tan y x =的图像可看出，(,0)2π是tan y x =的图像的一个对称中心．5．1000000tan 300cot(405)tan(36060)cot(36045)+-=-+--0000tan(60)cot(45)tan 60cot 451=-+-=--=．6．>13tan()tan()44ππ-=-，172tan()tan()55ππ-=-，又20254πππ-<-<-<，而tan y x =在(,0)2x π∈-内递增，则2tan()tan()45ππ->-，即可得．7．{,}24x k x k k Z ππππ-<<+∈可得1tan 0x ->，观察tan y x =的图像，注意tan y x =的周期为π，则定义域为{,}24x k x k k Z ππππ-<<+∈．8．解：可得πππk x +≠+232 ，z k ∈，即ππk x 23+≠，z k ∈， 所以函数的定义域是 {2,}3x x k k z ππ≠+∈．由2232x k k πππππ-+<+<+，z k ∈， 解得52233k x k ππππ-+<<+，z k ∈， 则知函数的单调区间为5(2,2)33k k k Z ππππ-++∈，且在其上为增函数．9．解：2tan 2tan 5y x a x =+⋅+22(tan )5x a a =+-+，[,)42x ππ∈，∴tan [1,)x ∈+∞，∴当1a ≤-时，25y a ≥-+，此时tan x a =-，则值域为2[5,)a -+∞； 当1a >-时，26y a ≥+，此时tan 1x =，则值域为[26,)a ++∞．备选题1．设θ是第二象限角，则〔 〕A ．tan12θ>B ．tan12θ<C ．sincos22θθ>D ．sincos22θθ<1．A θ是第二象限角，则222k k ππθππ+<<+，k Z ∈，则422k k πθπππ+<<+．当2,k n n Z =∈时，22422n n πθπππ+<<+，则tan12θ>；当21,k n n Z =+∈时，5322422n n θππππ+<<+，则tan 12θ>．2．函数tan()4y x π=-的定义域是．2．3{,}4x x k k Z ππ≠+∈知,42x k k Z πππ-≠+∈，则3,4x k k Z ππ≠+∈．同步测试题A 组一、选择题1．函数sin y x =的图像的一条对称轴方程是〔 〕A ．8x π=B ．54x π=C ．2x π=-D ．4x π=-2．1sin 、1cos 、1tan 的大小关系为( ) A ．1cos 1sin 1tan >> B ．1cos 1tan 1sin >> C ．1tan 1cos 1sin >> D ．1sin 1cos 1tan >>3．已知函数()sin 2x f x π+=，()tan()g x x π=-，则〔 〕A ．()f x 与()g x 都是奇函数B ．()f x 与()g x 都是偶函数C ．()f x 是奇函数，()g x 是偶函数D ．()f x 是偶函数，()g x 是奇函数4．下列各式中为正值的是〔 〕A ．37(tan1)cot 85ππ-B ．77sin tan88ππC ．cos6tan 6D ．00sin105cos 2305．对于下列四个命题：①sin()sin()1810ππ->-；②2517cos()cos()44ππ->-； ③00tan138tan143>；④00tan 40sin 40>．其中正确命题的序号是〔 〕A ．①③B ．①④C ．②③D ．②④ 6．若α是第一象限角，则ααααα2cos ,2tan ,2cos ,2sin,2sin 中能确定为正值的有〔 〕A ．0个B ．1个C ．2个D ．2个以上二、填空题7．平行于x 轴的直线与tan y x =的图像的相邻两个交点之间的距离为________．8．函数|tan |tan cos |cos ||sin |sin x xx x x x y ++=的值域是________．9．设,,A B C 是ABC ∆的三个内角，有下列4个关系式：①cos()cos B C A +=；②sin()sin A B C +=；③tan()tan A B C +=；④sin sin 22A B C+=．其中不正确的是______________．三、解答题10．已知tan 2α=-．〔1〕求2sin cos sin 2cos αααα+-；〔2〕求22sin 2cos 1αα-+．11．判断以下两个命题是否正确？并加以说明．〔1〕α、β都是第一象限角，若cos cos αβ>，则sin sin αβ>； 〔2〕α、β都是第四象限角，若sin sin αβ>，则tan tan αβ>．12．已知()sin f x a x b =+，5[0,]6x π∈，它的最大值为3，最小值为1．〔1〕求()f x 的表达式；〔2〕求使()2f x =成立的x 的值； 〔3〕求()f x 取最大值时x 的值．B 组一、选择题1．设()f x 是定义域为R ，最小正周期为32π的函数，若cos ,(0),()2sin ,(0).x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩ 则15()4f π-等于〔 〕A . 1B 2．0D ．22．cos cos y x x =-的值域是〔 〕A ．[1,0]-B ．[0,1]C ．[1,1]-D ．[2,0]-3．函数tan cos y x x =的部分图像是〔 〕A ．B ．C ．D ．4．已知14tan()15a π-=，那么14sin()15π-=〔 〕A ．21aa +-B ．21aa + C ．21||aa +D ．211a+-二、填空题5．已知0000cos(720)sin(540)()sin(360)tan(270)x x f x x x --=----，写出满足1()2f x =的一个x 值为_____． 6．在(0,2)π内，使sin cos x x >成立的x 取值范围为_________________．三、解答题7．已知α为第三象限角，且3sin()cos(2)tan()2()cot sin()f παπααπααπα-⋅-⋅-+=⋅+． 〔1〕化简()f α；〔2〕若31cos()25απ-=，求()f α的值．8．设关于x 的函数22cos 2cos (21)y x a x a =--+的最小值为()f a ． 〔1〕写出()f a 的表达式； 〔2〕试确定能使1()2f a =的a 值，并求出此时函数y 的最大值．答案A 组1．C 观察sin y x =的图像可以看出． 2．A tan1tan14π>=，又sin1sincoscos144ππ>=>，则1cos 1sin 1tan >>．3．D ()sin cos 2x f x x π+==，()tan()tan g x x x π=-=-，易判断()f x 是偶函数，()g x 是奇函数． 4．A 3tan tan 184ππ>=，72cot cot 055ππ=>，则37(tan 1)cot85ππ-为正值． 5．B 210182ππππ-<-<-<，则sin()sin()1810ππ->-，则①正确；画出040α=的正弦线和正切线，知④正确．6．C α是第一象限角，则2α在一或三象限，则tan 2α一定为正；2α的终边在x 轴的上方，则sin 2α一定为正．7．π相邻两个交点之间的距离就是tan y x =的图像的最小正周期π．8．{1,3}-知角x 的终边不会落在坐标轴上，分角x 的终边在第一、二、三、四象限内， y 的值分别为3、－1、－1、－1，则值域是{1,3}-．9．①③④ 知A B C π++=，则A B C π+=-，B C A π+=-．可得cos()cos B C A +=-，sin()sin A B C +=，tan()tan A B C +=-，sin cos 22A B C+=．则①③④不正确．10．解：〔1〕2sin cos 2tan 12(2)13sin 2cos tan 2224αααααα++⨯-+===----．〔2〕设角α的终边与单位圆的交点为(,)P x y ，则221x y +=，则sin y α=，cos x α=，那么22sin cos 1αα+=．222222222sin cos sin 2cos 12sin cos sin cos αααααααα--+=-=+222tan 17tan 15αα-==+． 11．解：〔1〕错误，可举例030α=，060β=，满足cos cos αβ>，但sin sin αβ<．〔2〕正确，证明如下：设12k απθ=+，k Z ∈，1(,0)2πθ∈-；22n βπθ=+，n Z ∈，2(,0)2πθ∈-．∵sin sin αβ>，∴12sin sin θθ>，而sin y x =在(,0)2x π∈-上为增函数，则2102πθθ-<<<，又tan y x =在(,0)2x π∈-上为增函数，则12tan tan θθ>，则tan tan αβ>．12．解：〔1〕知sin [0,1]x ∈，由已知可以得0a ≠． 当0a >时，max ()f x a b =+，min ()f x b =，则3a b +=，1b =，那么2,1a b ==，()2sin 1f x x =+．当0a <时，min ()f x a b =+，max ()f x b =，则1a b +=，3b =，那么2,3a b =-=，()2sin 3f x x =-+． 〔2〕若()2f x =，则有1sin 2x =，5[0,]6x π∈，则6x π=，或56x π=． 〔3〕当()2sin 1f x x =+时，由2sin 13x +=，则2x π=；当()2sin 3f x x =-+时，由2sin 33x -+=，则0x =．B 组1．B 1515333()(3)()sin 44244f f f πππππ-=-+⨯===． 2．D 可得0,cos 0,2cos ,cos 0.x y x x ≥⎧=⎨<⎩ 画出图像，则它值域为[2,0]-．3．C 当2x π=无意义，则A 、B 排除，当4x π=，y =，排除D ，知选C ．4．A 知1415π-是第三象限的角，则0a >，可设其终边上一点为(1,)P a --，则r OP ==14sin()15π-=5．030-00cos()sin(180)cos sin ()sin sin()tan(90)sin cot x x x x f x x x x x x --===----，由1sin 2x -=， 知满足它的一个x 值为030-． 6．5(,)44ππ在同一坐标系内画出sin y x =和cos y x =在(0,2)π内的图像，观察图像知使sin cos x x >成立的x 取值范围为5(,)44ππ．7．解：〔1〕sin cos cot ()cos cot (sin )f ααααααα⋅⋅==-⋅-．〔2〕331cos()cos()cos()sin 2225παππααα-=-=--=-=，则1sin 5α=-，则可设α的终边上一点为(1,)y -，得222(1)5y -+=，又0y <，则y =-cos α=，则()f α=． 8．解：〔1〕2222cos 2cos (21)2(cos )2122a a y x a x a x a =--+=----，cos [1,1]x ∈-，当112a-<<，即22a -<<时，2min 212a y a =---； 当12a≥，即2a ≥时，cos 1x =时，min 14y a =-； 当12a≤-，即2a ≤-时，cos 1x =-时，min 1y =．则21,2,1()21,22,214, 2.a f a a a a a a ≤-⎧⎪⎪=----<<⎨⎪-≥⎪⎩〔2〕由1()2f a =，得1a =-， 此时2112(cos )22y x =++，当cos 1x =时，y 有最大值为5．备选题1．下列函数是奇函数的是〔 〕A ．tan y x x =B ．sin tan y x x =C ．cos(sin )y x =D ．sin(tan )y x = 1．D 对于D 中函数，()sin[tan()]sin(tan )sin(tan )()f x x x x f x -=-=-=-=-， 其定义域关于原点对称，则sin(tan )y x =是奇函数．2．若函数2(sin )1y x a ＝－＋在sin 1x =时取最大值，在sin x a =时取得最小值， 则实数a 满足〔 〕A ．01a ≤≤B ．10a -≤≤C ．1a ≤-D ．1a ≥2．B 注意sin [1,1]x ∈-，函数2(sin )1y x a ＝－＋的对称轴为sin x a =， 由题意观察图像，则10a -≤≤．3．函数y =__________________．3．{22,}2x k x k k Z πππ-<≤∈ 可得cos 0x ≥，tan 0x ≤，则函数的图像可得{22,}22x k x k k Z ππππ-≤≤+∈，且{22,}2x k x k k Z πππ-<≤∈，求交集可得函数y ={22,}2x k x k k Z πππ-<≤∈．4．求证:ααααααααsin tan sin tan sin tan sin tan ⋅+=-⋅． 4．证明：设角α的终边上一点为(,)P x y，则r OP ==，则 222222(tan sin )(tan sin )tan sin y y x rαααααα-+=-=-22222222222222222211()tan sin r x y y y y y y x r x r x r x rαα-=-=⋅=⋅=⋅=⋅．∴ααααααααsin tan sin tan sin tan sin tan ⋅+=-⋅．。

（同步复习精讲辅导）北京市2014-2015学年高中数学 正弦函数y=sinx 的图像及图像变换课后练习一 新人教A 版必修4题一题面：在同一个坐标系内画,sin y x y x =-=的图 题二题面：在同一个坐标系内画sin ,2x y x y ==的图. 题三题面：将函数x y 4sin =的图象向左平移12π个单位，得到)4sin(ϕ+=x y 的图象，则ϕ等于( ) A ．12π-B ．3π-C ．3π D ．12π 题四题面：在同一个坐标系内画1()sin ,()f x x g x x==的图 题五题面：函数()y g x =过点(2，1)，则函数1()2y g x =的图像必过的点是 .题六题面：试述如何由y =31sin(2x +3π)的图象得到y =sin x 的图象.题七题面：函数2)62cos(-+=πx y 的图像F 按向量a 平移到F ’，F ’的解析式y =f (x )，当y =f (x )为奇函数时，向量a 可以等于( )A.)2,6(-πB.)2,6(πC.)2,6(--π D.)2,6(π-题八题面：已知电流I 与时间t 的关系式为sin()I A t ωϕ=+. (1)下图是sin()I A t ωϕ=+(ω＞0，||2πϕ<)在一个周期内的图象，根据图中数据求sin()I A t ωϕ=+的解析式；(2)如果t 在任意一段1150秒的时间内，电流sin()I A t ωϕ=+都能取得最大值和最小值，那么ω的最小正整数值是多少？课后练习详解题一答案：见详解 详解：题二答案：见详解 详解：题三 答案：C详解：函数x y 4sin =的图象向左平移12π个单位，得到)12(4sin π+=x y 的图象，故3πϕ= 题四答案：见详解 详解：题五答案：(4，1)详解：由题意: (2)1g =， 则1()2y g x =的图像必过的点是(4，1)题六答案：见详解. 详解：y =31sin(2x +3π)）（纵坐标不变倍横坐标扩大为原来的3πsin 312+=−−−−−−−−−→−x y x y sin 313π=−−−−−−−−→−纵坐标不变个单位图象向右平移x y sin 3=−−−−−−−−−→−横坐标不变倍纵坐标扩大到原来的题七 答案：D详解：∵cos(2)26y x π=+-，所以将函数cos(2)26y x π=+-向左平移6π个单位 得到cos 2()2cos(2)2sin 221262y x x x πππ=++-=+-=--，再向上平移2个单位 得到 y = x ，是奇函数，所以由平面向量平行规律可知，(,2)6a π=-，故选D.题八答案：(1)300sin(150)6I t ππ=+(2)ω＝943详解： (1)由图可知 A ＝300设t 1＝－1900，t 2＝1180， 则周期T ＝2(t 2－t 1)＝2(1180＋1900)＝175∴ ω＝2T π＝150π又当t ＝1180时，I ＝0，即sin(150π·1180＋ϕ)＝0，而||2πϕ<， ∴ ϕ＝6π. 故所求的解析式为300sin(150)6I t ππ=+.(2)依题意，周期T ≤1150，即2πω≤1150，(ω>0) ∴ω≥300π＞942，又ω∈N *，故最小正整数ω＝943.。

高一数学正弦函数图像及性质练习题π1.函数y=sin(4-2x)的单调增区间是〔〕A .[kπ-3π8,k3ππ+8](k∈Z) B.[kππ+8,k5ππ+8](k∈Z)C .[kπ-π8,k3ππ+8](k∈Z) D.[k3ππ+8,k7ππ+8](k∈Z)2.函数1y=5sin (3x-π3)的定义域是__________，值域是________，最小正周期是________，最值是________3.函数y=3sin〔1x－π〕.41〕用“五点法〞作函数的图象；2〕求此函数的最小正周期；3〕求此函数的单调递增区间.用五点法作出以下函数的图像：y 3sinx5.对于函数y=sin(13π-x〕，下面说法中正确的选项是2-----------------------------------------()( A)函数是周期为π的奇函数(B)函数是周期为π的偶函数( C)π(D)函数是周期函数是周期为2的奇函数6 .为2π的偶函数作出函数6.y3sin(2x3R：),x3（1〕求此函数的周期、最值和取最值时X的集合；2〕求此函数的单调区间。

7.函数ysin(2x 5)的图像的单调区间是28.求函数的周期、最值及取得最值时X的集合（9.用五点作图法画出函数图像1〕求函数的周期T=？2〕求函数最值及取最值时X的集合。