三角函数图像及其变换

三角函数图像的变换与特征三角函数图像的变换是数学中一个重要的概念，它描述了三角函数图像相对于原始函数图像的位置、形状和特征的变化。

在本文中，我们将探讨三角函数的变换和它们的特征。

一、平移变换平移是指将函数图像沿着横轴或纵轴方向移动的操作。

对于三角函数而言，平移的规律如下：1. 正弦函数（Sine Function）的平移：a. 沿横轴平移：f(x) = sin(x - a)，其中a为平移的距离，若a > 0，则向右平移；若a < 0，则向左平移。

b. 沿纵轴平移：f(x) = a + sin(x)，其中a为平移的距离，若a > 0，则向上平移；若a < 0，则向下平移。

2. 余弦函数（Cosine Function）的平移：a. 沿横轴平移：f(x) = cos(x - a)，其中a为平移的距离，若a > 0，则向右平移；若a < 0，则向左平移。

b. 沿纵轴平移：f(x) = a + cos(x)，其中a为平移的距离，若a > 0，则向上平移；若a < 0，则向下平移。

二、伸缩变换伸缩是指对函数图像进行拉伸或压缩的操作。

对于三角函数而言，伸缩的规律如下：1. 正弦函数的伸缩：a. 沿横轴伸缩：f(x) = sin(kx)，其中k为伸缩的系数，若k > 1，则图像水平方向收缩；若0 < k < 1，则图像水平方向拉伸。

b. 沿纵轴伸缩：f(x) = a * sin(x)，其中a为伸缩的系数，若a > 1，则图像垂直方向收缩；若0 < a < 1，则图像垂直方向拉伸。

2. 余弦函数的伸缩：a. 沿横轴伸缩：f(x) = cos(kx)，其中k为伸缩的系数，若k > 1，则图像水平方向收缩；若0 < k < 1，则图像水平方向拉伸。

b. 沿纵轴伸缩：f(x) = a * cos(x)，其中a为伸缩的系数，若a > 1，则图像垂直方向收缩；若0 < a < 1，则图像垂直方向拉伸。

三角函数图像的变换一．x y sin =图像的三种变换：①函数x y sin =的图象上所有点向左（右）平移ϕ个单位长度，得到函数()sin y x ϕ=+的图象；再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长（缩短）到原来的1ω倍（纵坐标不变），得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象． ②数sin y x =的图象上所有点的横坐标伸长（缩短）到原来的1ω倍（纵坐标不变），得到函数sin y x ω=的图象；再将函数sin y x ω=的图象上所有点向左（右）平移ϕω个单位长度，得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象． 二．函数()()sin 0,0y x ωϕω=A +A >>的性质： ①振幅：A ；②周期：2πωT =；③频率：12f ωπ==T ；④相位：x ωϕ+；⑤初相：ϕ． 函数()sin y x ωϕ=A ++B ，当1x x =时，取得最小值为min y ；当2x x =时，取得最大值为max y ，则()max min 12y y A =-，()max min 12y y B =+，()21122x x x x T=-<．三．练习1.已知简谐运动()2sin()()32f x x ππϕϕ=+<的图象经过点(0，1)，则该简谐运动的最小正周期T =_________；初相ϕ=__________．2.三角方程2sin(2π－x )=1的解集为_______________________． 3.函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为______________________．{2,}3x x k k Z ππ=±∈ )48sin(4π+π-=x y第3题4.要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象向右平移__________个单位．5.为了得到函数R x x y ∈+=),63sin(2π的图像，只需把函数2sin y x =，x R ∈的图像上所有的点①向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变）；②向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变）；③向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）； ④向右平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）．其中，正确的序号有_____③______． 6.为了得到函数)62sin(π-=x y 的图象，可以将函数x y 2cos =的图象向右平移__3π__个单位长度．7.若函数()2sin()f x x ωϕ=+，x ∈R （其中0ω>，2ϕπ<）的最小正周期是π，且(0)f =ω=______；ϕ=__________．8.下列函数： ①sin 6y x π⎛⎫=+⎪⎝⎭； ②sin 26y x π⎛⎫=-⎪⎝⎭； ③cos 43y x π⎛⎫=-⎪⎝⎭； ④cos 26y x π⎛⎫=-⎪⎝⎭． 其中函数图象的一部分如右图所示的序号有_____④_____． 9.函数y =sin(2x +3π)的图象关于点_______________对称． 10.求下列函数的单调减区间： （1）⎪⎭⎫⎝⎛+=62cos 2πx y （2）⎪⎭⎫ ⎝⎛+-=32sin 2πx y 11. 函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是___________________12. 7．如图，函数π2cos()(00)2y x x >ωθωθ=+∈R ，，≤≤的图象与y轴相交于点(0，且该函数的最小正周期为π．（1）求θ和ω的值；π6第8题（2）已知点π2A⎛⎫⎪⎝⎭，，点P是该函数图象上一点，点00()Q x y，是PA当y=ππ2x⎡⎤∈⎢⎥⎣⎦，时，求x的值．13.设函数)(),()2sin()(xfyxxf=<<-+=ϕπϕ图像的一条对称轴是直线8π=x．（Ⅰ）求ϕ；（Ⅱ）求函数)(xfy=的单调增区间；（Ⅲ）画出函数)(xfy=在区间],0[π上的图像第7题。

三角函数图像与变换一、引言三角函数是高中数学中的重要内容，它们在数学和物理等领域都有广泛的应用。

本文将从三角函数的图像出发，探讨其与变换的关系，并探讨它们在实际问题中的应用。

二、三角函数的基本图像1. 正弦函数的图像正弦函数是最基本的三角函数之一，它的图像呈现周期性的波动形态。

当自变量为0时，正弦函数的值为0；当自变量为90度（或π/2弧度）时，正弦函数的值为1；当自变量为180度（或π弧度）时，正弦函数的值为0；当自变量为270度（或3π/2弧度）时，正弦函数的值为-1；以此类推，正弦函数的图像在每个周期内都呈现出上升、下降、上升、下降的特点。

2. 余弦函数的图像余弦函数与正弦函数非常相似，它们的图像在形态上只有一个平移。

当自变量为0时，余弦函数的值为1；当自变量为90度（或π/2弧度）时，余弦函数的值为0；当自变量为180度（或π弧度）时，余弦函数的值为-1；当自变量为270度（或3π/2弧度）时，余弦函数的值为0；以此类推，余弦函数的图像也呈现出上升、下降、上升、下降的特点。

3. 正切函数的图像正切函数是另一个重要的三角函数，它的图像呈现出周期性的波动形态。

正切函数的图像在每个周期内都有一个渐进线，即在自变量接近90度（或π/2弧度）和270度（或3π/2弧度）时，函数值趋近于无穷大。

三、三角函数的变换1. 平移变换平移变换是指将函数的图像沿x轴或y轴方向移动一定的距离。

对于正弦函数和余弦函数，平移变换可以通过改变自变量的值来实现。

例如，将正弦函数的自变量增加π/4，可以使函数图像向左平移π/4个单位；将正弦函数的自变量减少π/4，可以使函数图像向右平移π/4个单位。

同样的，对于余弦函数，也可以通过改变自变量的值来实现平移变换。

2. 伸缩变换伸缩变换是指将函数的图像在x轴或y轴方向进行拉伸或压缩。

对于正弦函数和余弦函数，伸缩变换可以通过改变自变量的系数来实现。

例如，将正弦函数的自变量乘以2，可以使函数图像在x轴方向压缩一倍；将正弦函数的自变量除以2，可以使函数图像在x轴方向拉伸一倍。

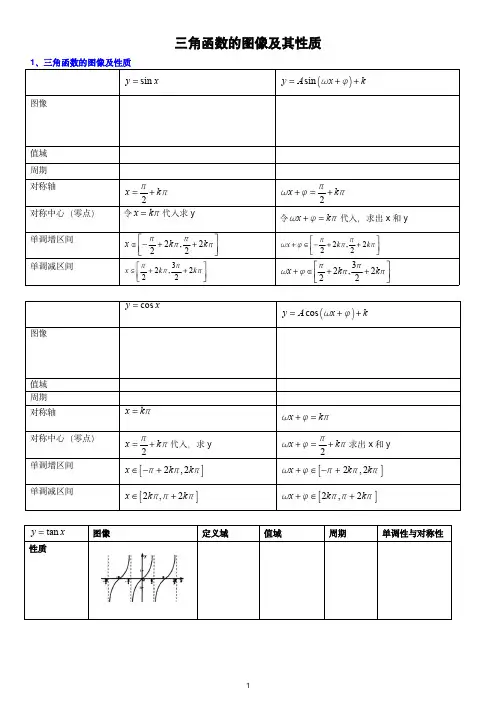
三角函数的图像及其性质1、三角函数的图像及性质sin y xsin y A x k图像值域周期对称轴2x k2x k对称中心（零点）令x k 代入求y令x k 代入，求出x 和y 单调增区间2,222x k k2,222x k k单调减区间32,222x k k32,222x k kcos y xcos y A x k图像值域周期对称轴x kx k 对称中心（零点）2x k代入，求y 2x k求出x 和y 单调增区间 2,2x k k 2,2x k k 单调减区间2,2x k k2,2x k k tan y x图像定义域值域周期单调性与对称性性质【考点分类】考点一：图像变换：1．把函数y ＝sin x 的图象向右平移个单位得到y ＝g （x ）的图象，再把y ＝g （x ）图象上所有点的纵坐标伸长到原来的2倍（横坐标不变），所得到图象的解析式为（）A．B．C．D．2．将函数f （x ）＝sin x 图象上所有点的横坐标变为原来的（ω＞0），纵坐标不变，得到函数g （x ）的图象，若g （x ）的最小正周期为6π，则ω＝（）A．B．6C．D．33．将函数y ＝2sin2x 图象上的所有点向右平移个单位，然后把图象上所有点的横坐标缩短为原来的倍，（纵坐标不变）得到y ＝f （x ）的图象，则f （x ）等于（）A．2sin（x ﹣）B．2sin（x ﹣）C．2sin（4x ﹣）D．2sin（4x ﹣）4．已知曲线C 1：y ＝cos x ，C 2：y ＝sin（2x +），则下面结论正确的是（）A．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再向右平移个单位长度，得到曲线C 2B．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再向左平移个单位长度，得到曲线C 2C．把C 1上各点的横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度，得到曲线C 2D．把C 1上各点的横坐标缩短到原来的，纵坐标不变，再向左平移个单位长度，得到曲线C 25.把函数y ＝cos(3x ＋4)的图象适当变动就可以得到y ＝sin(－3x )的图象，这种变动可以是()A 向右平移4 B 向左平移4 C 向右平移12 D 向左平移126..函数32sin( x y 的图象是由2sin xy 的图象沿x 轴（）得到的。

三角函数b x A y ++=)sin(ϕω的图像变换三角函数的图像变换是历年来高考的重点内容，因此我们有必要对这一问题作一下研究。

下面就三角函数的图像变换的基本题型，做以详细讲析：一、 振幅变换由函数)(x f y =的图像变换为)(x Af y =的图像，其主要的方法是将)(x f y =图像上的各点的纵坐标变为原来的A 倍，即)()(A x Af y x f y =−−−−−−→−=倍纵坐标变为原来的。

例1、要得到)32sin(4π-=x y 的图像，只需将)32sin(π-=x y 的图像( )。

A 、 向上平移4个单位；B 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍； C 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4-倍； D 、 向下平移4个位单位。

分析：由题意可知，将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍，就可以得到)32sin(4π-=x y 的图像。

故选B 。

二、 周期变换由函数)(x f y =的图像变换为)(x f y ω=的图像，其主要的方法是将)(x f y =图像上的各点的横坐标变为原来的ω1倍，即)()(1x f y x f y ωω=−−−−−−→−=倍横坐标变为原来的。

例2、如何由x y sin =的图像得到x y 2sin 2=的图像。

解：由x y sin =的图像上各点的纵坐标伸长到原来的2倍，得到x y sin 2=的图像，再将x y sin 2=的图像各点的横坐标压缩为原来的21倍，得到x y 2sin 2=的图像。

三、 相位变换(左右平移变换)由函数)(x f y =的图像变换为)(ϕ+=x f y 的图像，其主要的方法是将)(x f y =图像上所有点向左或向右平移ϕ个单位。

即)()(0)(ϕϕϕ+=−−−−−−→−=>x f y x f y 个单位向左平移 )()(0)(ϕϕϕ-=−−−−−−→−=>x f y x f y 个单位向右平移 例3、如何由)32sin(31π+=x y 的图像得到x y sin =的图像。