2015秋湘教版九年级数学上册第4章《锐角三角形》检测题及答案
- 格式:doc
- 大小:190.24 KB
- 文档页数:5

【九年级】九年级上册数学第4章锐角三角函数测试(湘教版带答案)来来源第4章锐角三角函数检测题(时间:90分钟,满分:100分)一、(每小题3分,共30分)1.计算:a.b.c.d.2.在△, ∠ = 90°,如果,,那么sin的值是()a.b.c.d.3.在△, ∠ = 90,然后是罪()a.b.c.d.4.在下列陈述中,正确的是()a.b、如果是锐角,那么c.对于锐角,必有D5.在△中,∠=90°,,则sin的值是()a、 b.c.1d。
6.已知在中,,则的值为()a、不列颠哥伦比亚省。
7.如图,一个小球由地面沿着坡度的坡面向上前进了10,此时小球距离地面的高度为()a、 b.2c.4d.8.如图所示,在钻石中,,,Tan的值∠ 是()a.b.2c.d.9.在△,,, 等于()a.b.1c.2d.310.如图所示,已知45°<a<90°,则以下公式为真()a.b.c、 d。
二、题(每小题3分,共24分)11.那么__12.若∠是锐角,cos=,则∠=_________.13.小兰想测量南塔的高度她抬头看了看塔顶,测量了30°的仰角,然后向塔的方向移动了50°,测量了60°的仰角,所以塔的高度大约是___________________14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.15.大坝的横截面为梯形。
坝内坡度和坝外坡度是两个坡度角的总和16.△abc的顶点都在方格纸的格点上,则_.在图中,四边形18.如图,在△中,已知,,,则________.三、回答问题(共46分)19.(8分)计算下列各题:(1);(2).20.(6分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在树前的平地上选择一个点,测量树顶与该点的仰角为35°;(2)在点和大树之间选择一点(、、在同一条直线上),测得由点看大树顶端的仰角恰好为45°;(3)两个测量点之间的距离为4.5请你根据以上数据求出大树的高度.(结果保留3个有效数字)21.(6点)已知:如图所示,在山脚处测得的山顶仰角为,沿坡度前进米,以坡度角到达(即。

第四章 锐角三角函数检测题 (时间:90分钟,满分:100分)一.选择题(每小题3分,共30分) 1.计算:A. B.232+ C.23 D.231+2.在△中,∠=90°,如果,,那么sin 的值是( ). A.21B.55 C.33 D.233.(4分)如图,△ABC 中,∠B =90°,BC =2AB ,则cos A =( ) A. B. C. D.4.下列说法中,正确的是( ) A.B.若为锐角,则C.对于锐角,必有sin cos ββ<D.5.如图,在网格中,小正方形的边长均为1,点A ,B ,C 都在格点上,则∠ABC 的正切值是( )A.2B.C.D.6.已知在Rt ABC △中,390sin 5C A ∠==°,,则tan B 的值为( )A.43B.45C.54D.347.如图,一个小球由地面沿着坡度的坡面向上前进了10 m ,此第7题图A BC第10题图时小球距离地面的高度为( ) A.B.25m C.45m D.310m 8.如图,在菱形ABCD 中,,3cos 5A =,BE =2,则tan ∠DBE 的值是( )A.12B.2C.5D.59.在△中,,,,则等于( )A. B.1 C.2 D.3 10.如图,已知:45°<A <90°,则下列各式成立的是( ) A.sin A =cos AB. sin A ﹥cos AC. sin A ﹥tan AD. sin A ﹤cos A 二.填空题(每小题3分,共24分)11.在Rt ABC △中,90C ∠=,5AC =,4BC =,则tan A =______. 12.如图,△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE ,若BE =9,BC =12,则cos C =___________.13.如图,小兰想测量南塔的高度, 她在A 处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m 至B 处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计,732.13≈) 14.等腰三角形的腰长为2,腰上的高为1,则它的底角等于________ . 15.大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个坡角的和为 .16.如图,△ABC的顶点都在网格纸的格点上,则_ . 17. 如图,在四边形中,,,,,则__________.18. 如图,在△中,已知,,,则________. 三.解答题(共46分) 19.(8分)计算下列各题: (1) ()42460sin 45cos 22+- ; (2)2330tan 3)2(0-+--.20.(6分)如图,AD 是△ABC 的中线,tan B =,cos C =,AC =.求: (1)BC 的长;(2)sin ∠ADC 的值.20题图21.(6分)已知:如图,在山脚的处测得山顶的仰角为,沿着坡角为的斜坡前进m 到达处(即∠,m ),测得的仰角为,求山的高度.22.(6分)如图,为了测量某建筑物CD 的高度,先在地面上用测角仪自A 处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m ,此时自B 处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m ,请你计算出该建筑物的高度.(3≈1.732,结果精确到1 m )23.(6分)如图,在梯形中,∥,,.ABCD第21题图(1)求sin∠DBC的值;(2)若长度为,求梯形的面积.24.(6分)如图,在小山的东侧A处有一热气球,以每分钟30 m的速度沿着仰角为60°的方向上升,20 min后升到B处,这时热气球上的人发现在A的正西方向俯角为45°的C处有一着火点,求热气球的升空点A与着火点C的距离(结果保留根号).25.(8分)如图,平台AB高为12 m,在B处测得楼房CD顶部点D 的仰角为45°,底部点C的俯角为30°,求楼房CD的高度.( 1.7)第24题图BC A 东西45°60°参考答案1.B解析:方法1:∵∴,∴∴ 这个直角三角形的斜边长是3,故选B.方法2:设1x 和2x 是方程22870x x -+=的两个根,由一元二次方程根与系数的关系可得∴22221212127()24292x x x x x x +=+-=-⨯=,∴ 这个直角三角形的斜边长是3,故选B.2.B 解析:∵ 22141411104b ac -=-⨯⨯=-=,∴ 一元二次方程+x +=0有两个相等的实数根. 3.B 解析:设第一块木板的宽是,则第一块木板的长是,第二块木板的长是,第二块木板的宽是.根据题意,得3(22)2108x x x x --⋅=. 整理,得223540x x --=,因式分解,得(6)(29)0x x -+=,解得1296,2x x ==-. ∵ 292x =-不合题意,舍去.∴ 6x =. ∴ 第一块木板长,宽,第二块木板长,宽.4.B 解析:过作的平行线交于,则△∽△.∵ 是的中点,∴ ,,∴A BEF CD第4题答图G∴ AC =AF +FG +GC =4+8+8=20(cm ).故选B. 5.C 解析 :∵ AB AC =,∴ ABC ACB ∠=∠. 又∵ CBD A ∠=∠,∴ △ABC ∽△BCD . 同理可得△ABC ∽△BCD ∽△CDE ∽△DFE , ∴,,AB BC CD DE EF DEBC CD BD CD DE CE===,解得23423,,b b b CD DE EF a a a===.故选C.6. C 解析:根据题意,得AB ⊥PB ,∠ABP =90°,在Rt △ABP 中,∠PAB =55°,PA =2海里,cos AB PAB PA∠=,∴ cos AB PA PAB =⋅∠=2cos 55°海里,故选项C 正确.7.C 解析:平均成绩相同,方差反映数据的稳定性,方差越小成绩越稳定.8.A 解析:如图,过点A作因为22,所以.由勾股定理,得.又53, 所以所以 第8题答图所以所以9.D 解析:如图,过点C 作CD AB ⊥于点D .设AC x =海里.在△ACD 中,∠90ADC =︒,∠102030CAD =︒+︒=︒,第9题答图AC x =海里,∴ C D =12AC =12x 海里,AD =3CD =32x 海里. 在△BCD 中,∠90BDC =︒,∠802060CBD =︒-︒=︒, ∴ BD =33CD =36x 海里. ∵ AD BD AB +=,∴ 32x +36x 20=, 解得103x =,所以救援船航行的速度为2010330360÷=(海里/时). 10.B 解析:因为,,所以,所以A =90°-A ,所以A =45°. 11.2560x x -+= 12.0x =或3x =13.3tan 50° 解析:在Rt △ABC 中,∵∠C =90°,∠A =40°, ∴ ∠B =50°,∴ tan B =tan 50°=BCAC, ∴ AC =BC tan 50°=3 tan 50°.14. 3 4 解析:设方程的另一个根为a ,根据根与系数的关系得到a ×1=3,a +1=m , 解得a =3,m = 4. 15.3 解析:∵ ,∠为△和△的公共角,∴ △∽△,∴.在Rt △中,由勾股定理得,得. 又∵,,,∴,∴.16. 变大 解析:减少木工2名,增加电工.瓦工各1名后,14名员工的工资少了两个6 000,多了一个7 000和一个5 000,调整前后工程队员工月平均工资不变,均是6 000元,但调整后各数据与平均数的差的平方和变大了,所以方差变大了. 17. 135 解析:在Rt △ABD 中,∠BAD =90°,=, ∵ ∠ADB =30°,AB =45 m ,∴ =,∴ AD =45m.在Rt △ADC 中,∠ADC =90°,=, ∵ ∠CAD =60°,AD =45m ,∴=,∴ DC =135 m.18. 6 解析:如图,连接OA ,OB ,OC ,OD ,设DC ,AB 分别交y 轴于点F ,E ,则S △AOB =12OE ·AB =32OE =12a -12b ,S △COD =12OF ·CD =12×OF ×2=12a -12b ,∴ 325,OE OF OE OF ⎧=⎪⎨⎪+=⎩,解得2,3,OE OF =⎧⎨=⎩∴ 12a -12b =3,∴ a -b =6.19.解:(1)55sin 35sin 12145sin 222+++-2222(21)sin 35cos 352⨯--++22.(2)12︒-30tan 3+121-⎪⎭⎫ ⎝⎛-2133332-+⨯-=13-=. 20.解:设矩形猪舍垂直于住房墙的一边长为x m,则矩形猪舍的另一边长为(26-2x )m.根据题意,得x (26-2x )=80. 化简,得-13x +40=0. 解这个方程,得=5,=8.当x =5时,26-2x =16>12(舍去);当x =8时,26-2x =10<12.答:所建矩形猪舍的长为10 m,宽为8 m 时,猪舍面积为80 m 2. 21.解:(1)过点C 作CE ∥OA 交BD 于点E ,则△BCE ∽△BOD . 又C 为OB 的中点,所以BC OC =,所以1122CE OD AD ==. 再由CE ∥OA ,△ECP ∽△DAP ,所以2==CEADPC AP . (2)过C 作CE ∥OA 交BD 于点E ,设AD x =,则4OA OB x ==,3OD x =, 由△BCE ∽△BOD ,得1322CE OD x ==. 再由△ECP ∽△DAP ,得32==CE AD PE PD . 由勾股定理可知5BD x =,52DE x =,则32=-PD DE PD ,可得PD AD x ==, 则∠BPC =∠DPA =∠A ,所以tan ∠BPC =tan ∠A =21=AO CO . 22.(1)证明:AB ∥DC ,∴ ACF CAE =∠∠.在△CFO 和△AEO 中,∴ △≌△CFO AEO ,∴ OF OE =.又 OA OC =,∴ 四边形AECF 是平行四边形. EF AC ⊥,∴ 四边形AECF 是菱形.(2)解: 四边形AECF 是菱形,4EF =,∴ 114222OE EF ==⨯=. 在Rt AEO △中, 2tan 5OE OAE OA ==∠,∴ 5OA =, ∴ 22510AC AO ==⨯=.∴23.解:设B 处距离码头O x km. 在Rt △CAO 中,∠CAO =45°. ∵ tan ∠CAO =∴ CO =AO ·tan ∠CAO =(45×0.1+x )·tan 45°=4.5+x. 在Rt △DBO 中,∠DBO =58°.∵ tan∠DBO=,∴DO=BO·tan∠DBO=x·tan 58°.∵DC=DO CO,∴ 36×0.1= x·tan 58°(4.5+x),∴x=≈=13.5.因此,B处距离码头O大约13.5 km.24.解:(1)10÷25%=40;(2)补全条形统计图如下:第24题答图40×30%=12,40-10-15-12=3.(3)1 200× =90.答:估计全校最喜爱篮球的人数比最喜爱足球的人数多90人. 25.(1)证明:由题意可知∵∥∴∠∠,∠=∠∴△≌△∴.又∥∴四边形是平行四边形.∵,∴平行四边形是菱形.(2)解:∵四边形是菱形,∴.设,∵△的面积为24,△的周长为.(3)解:存在,过点作的垂线,交于点,点就是符合条件的点.证明如下:∵ ∠∠90°,∠∠ ∴ △∽△,∴ AE AO AP AE ,∴ . ∵ 四边形是菱形,∴ ∴∴。
新湘教版九年级数学上册第四章《锐角三角》检测题时间: 120 分钟满分:120 分一、选择题 (本大题共1.如图,在 Rt△ ABC 则 sin∠ACD 的值为 (A 10 个小题,每题 3 分,共 30 分)中,∠ ACB= 90°,CD⊥ AB,垂足为点)D,若AC=5,BC= 2,A.53B.2555C. 22D. 3,第 1题图),第 2题图),第 4题2.如图,在边长为图 )1 的小正方形构成的网格中,第 5 题图),△ ABC 的三个极点均在格点上,则tanA=(D)3 A. 54B. 534D. 33.计算sin30°· tan45°的结果是(A)1 A. 23B. 23C. 6D.244.如图,在Rt△ ABC 中,∠ ACB=90°,BC= 1,AB= 2,则以下结论正确的选项是(D)313A . sinA=2B. tanA= 2C. cosB=2 D .tanB=35.如图,AC 是电杆的一根拉线,测得 BC= 6 米,∠ ACB=52°,则拉线 AC 的长为 ( D )6米 B.6米C. 6·cos52°米 D.6米A.sin52°tan52°cos52°6.(2014·德州 )如图是拦水坝的横断面,斜坡 AB 的水平宽度为12 米,斜面坡度为 1∶2,则斜坡 AB 的长为 ( B )A.4 3米B. 65米C.12 5米D.24 米37.在△ ABC 中,∠ C= 90°, tanA=4,则 cosB 的值是 ( C)4334A. 5B. 4C.5D.38.如图,渔船在 A 处看到灯塔 C 在北偏东 60°方向上,渔船向正东方向航行了12 海里抵达 B 处,在 B 处看到灯塔 C 在正北方向上,这时渔船与灯塔C的距离是 ( D) A.12 3海里 B.6 3海里C.6 海里 D.4 3海里9.如图,为丈量 B 点到河岸 AD 的距离,在 A 点测得∠ BAD=30°,在 C 点测得∠ BCD =60°,又测得 AC= 100 米,则 B 点到河岸 AD 的距离为 ( B )A.100 米 B.50 3米 C.2003米 D.50 米3,第9 题图),第10题图)上走10.(2014·深圳 )小明去登山,在山脚看山顶角度为1300 米,此时小明看山顶的角度为60°,求山高(30°,小明在坡比为B)5∶ 12 的山坡A . (600- 250 3)米B. (6003- 250)米C.(350 + 350 3)米D. 500 3米二、填空题 (本大题共8 个小题,每题 3 分,共 24分 )4 11.在 Rt△ABC 中,∠C= 90°,假如 AC= 3, AB= 5,那么 cosB 的值是 __5__.212.在△ ABC 中,∠ C=90°, BC= 2, sinA=3,则 AC 的长是 __5__.13.如图,在地面上的点 A 处测得树顶 B 的仰角为α度,AC= 7 米,则树高 BC 为 __7tanα__米. (用含α的代数式表示 ),第 13题图),第 14题图),第16题图),第 17题图)14.如图,△ ABC 中,∠C= 90°,BC= 4 cm,tanB=32,则△ ABC 的面积是 __12__cm2.15.在△ ABC 中,若∠ A,∠ B 知足 |cosA-1|+ (sinB-2)2= 0,则∠ C=__75° __.2216.长为 4 m 的梯子搭在墙上与地面成45°角,作业时调整为60°角 (如下图 ),则梯子的顶端沿墙面高升了 __(2 3-2 2)__m.17.(2014·襄阳 )如图,在建筑平台 CD 的顶部 C 处,测得大树 AB 的顶部 A 的仰角为45°,测得大树 AB 的底部 B 的俯角为 30°,已知平台 CD 的高度为 5 m,则大树的高度为__(5+53)__m.(结果保存根号)18.(2014·宜宾 )规定:sin(- x)=- sinx,cos(- x)= cosx,sin(x+ y)= sinx·cosy+ cosx·siny.据此判断以下等式建立的是__②③④ __. (写出全部正确的序号)① cos(- 60°) =-1;②sin75°=6+2;③ sin2x= 2sinx·cosx;④ sin(x- y)= sinx·cosy 24-c osx· siny.三、解答题 (66 分 )19. (8 分) 计算:(1)sin230°+ cos245°+3sin60°· tan45°;9解:422(2)cos 30°+ cos 60°+sin245°.3解:220. (8 分) 在 Rt△ ABC 中,∠ C=90°, a= 10, c=20,解这个直角三角形.解:∠ A =30°,∠B= 60°, b=10321. (8 分 )假如是我国某海疆内的一个小岛,其平面图如图甲所示,小明据此结构出该岛的一个数学模型如图乙所示,此中∠ B=∠ D= 90°,AB= BC= 15 千米,CD= 3 2千米.求∠ACD 的余弦值.解:连结 AC ,在 Rt △ABC 中,AC =AB 2+ BC2= 15 2千米,在 Rt△ ACD 中,cos∠ACD =CD=32 = 1, ∴∠ ACD 的余弦值为 1 AC15 2 5 5122. (10 分 )如图 ,在 Rt △ABC 中, ∠ C = 90°, BC = 8, tanB = 2,点 D 在 BC 上,且 BD =AD.求 AC 的长和 cos ∠ ADC 的值.1解:∵在 Rt △ ABC 中, BC =8, tanB = 2, ∴AC = 4.设 AD = x ,则 BD = x ,CD = 8- x ,由勾股定理 ,得 ( 8- x )2+ 42= x 2.解得 x =5.∴ cos ∠ ADC = DC = 3AD 523. (10 分 )(2014·常德 )如图 , A , B , C 表示修筑在一座山上的三个缆车站的地点,AB , BC 表示连结缆车站的钢缆.已知A ,B ,C 所处地点的海拔 AA 1, BB 1, CC 1 分别为160 米,400 米,1000 米,钢缆 AB ,BC 分别与水平线 AA 2,BB 2 所成的夹角为 30° ,45° ,求钢缆 AB 和 BC 的总长度. (结果精准到 1 米 )解:依据题意知BD = 400- 160= 240 米, CB 2= 1000- 400=600 米,在 Rt △ ADB中,sin30°=BD,∴ AB =BD = 480 米,在 Rt △BB2C 中, °= CB 2,∴BC = CB 2ABsin30°sin45 BC sin45°= 600 2米, AB + BC = (480+ 600 2)米≈ 1329 米24. (10 分 )如图 ,某高速公路建设中需要确立地道AB 的长度.已知在离地面 1500 m的高度 C 处的飞机上 ,丈量人员测得正前面 A ,B 两点处的俯角分别为 60°和 45° .求地道AB 的长. ( 3≈ 1.73)解:∵ OA = 1500× tan30 °= 500 3,OB= OC =1500 ,∴ AB= 1500- 5003≈ 1500-865= 635(m)25. (12 分 )我市某中学在创立“特点校园”的活动中,将本校的办学理念做成宣传牌AB,搁置在教课楼的顶部(如下图 ).小明在操场上的点 D 处,用 1 米高的测角仪CD,从点 C 测得宣传牌的底部 B 的仰角为37°,而后向教课楼正方向走了 4 米抵达点 F 处,又从点 E 测得宣传牌的顶部 A 的仰角为45° .已知教课楼高BM =17 米,且点 A, B, M 在同一直线上,求宣传牌 AB 的高度. (结果精准到0.1 米,参照数据:3≈, sin37°≈,cos37°≈, tan37°≈ 0.75)解:过点 C 作 CN ⊥AM AN = x+(17- 1)= x+ 16(米),在于点 N ,则点 C , E, N 在同向来线上.设AB= x 米,则 Rt △AEN 中,∠ AEN =45°,∴ EN =AN = x+ 16,在 RtBN17- 131△BCN 中,∠ BCN = 37°,BM = 17,∴ tan∠ BCN =CN=,∴x+20=4,解得 x= 13≈1AB 的高度约为 1.3 米1.3.经查验: x= 13是原分式方程的解.答:宣传牌。

第4章锐角三角函数一、选择题1.tan60°的值等于()A. B. C. D.2.在Rt△ABC中,∠C=90o,AC=4,AB=5,则sinB的值是 ( )A. B. C. D.3.如果∠α是等腰直角三角形的一个锐角,则cosα的值是()A. B. C. 1 D.4.如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是()米.A. 1.2B. 1.1C. 0.8D. 2.25.在△ABC中,∠C=90°,AB=15,sinA=,则BC等于()A. 45B. 5C.D.6.王芳同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王芳同学离A地()A. 50mB. 100mC. 150mD. 100m7.计算sin45°的结果是( )A. B. 1 C. D.8.某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:≈1.4)()A. B. C. D.9.如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=()A. B. 1 C. D.10.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为()A. 56米B. 66米C. (56+20)米D. (50+20)米二、填空题11.若,则锐角α=________.12.一条斜坡长4米,高度为2米,那么这条斜坡坡比i=________ .13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=,那么BC=________14.如图,河堤横断面如图所示,迎水坡AB的坡比为1:,则坡角∠A的度数为________15.在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)16.如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是________米(结果保留根号).17.在Rt 中,,,则的值为________.18.在正方形网格中,△ABC的位置如图所示,则tanB的值为________.19.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为________厘米(结果保留根号).三、解答题20.如图,已知∠B=90°,AB=2cm,BC=2cm,CD=3cm,AD=5cm,求四边形ABCD的面积.21.马航MH370 客机“失联”,我国“海巡01号”前往搜寻。

湘教版九年级数学上册第4章锐角三角函数测试题一、选择题。
(每小题只有一个正确答案)1.已知在R t △ABC 中,∠C = 90°,∠A =α,AB = 2,那么BC 的长等于 A .2sin αB .2cos αC .2sin αD .2cos α2.如图,已知Rt △ABC 中,∠C =90°,BC =3, AC =4,则sinA 的值为( ).A .34B .43C .35D .453.如图,在平面直角坐标系中,点A 的坐标为()4,3,那么sin α的值是( )A .34B .43C .45D .354.△ABC 中,∠C=90°,BC=12,AB=13,那么sinA 的值等于( )A .513B .1213C .512D .1255.在△ABC 中,若21cos (1tan )2A B -+-=0,则∠C 的度数是( )A .45°B .60°C .75°D .105°6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC BC=2,则sin∠ACD 的值为()A B C D.2 37.小明沿着坡比为1600m,则他升高了()A.B.C.300 m D.200m8.如图,在菱形ABCD中,DE⊥AB于E,cosA=35,BE=2,则tan∠DBE的值是()A.2 B.12C D9.在△ABC中,若|sinA﹣12|+tanB)2=0,则∠C的度数为()A.30°B.60°C.90°D.120°10.已知α是锐角,且点A(12,a),B(sinα+cosα,b),C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是()A.a<b<c B.a<c< b C.b<c<a D.c<b<a 二、填空题11.ABC中,∠C=90°,AB=8,cosA=34,则BC的长_____.12.如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=____.13.某人沿着坡度为1:3的山坡向上走了200m,则他升高了________米.14.已知α、β是锐角,且cotα<cotβ,则α、β中较小的角是________.15.已知在Rt △ABC 中,∠C=90°,tanA=34, 则sinA=________ .16.小聪家对面新建了一幢图书大厦,他在A 处测得点D 的俯角α为30°,测得点C 的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC 为30米,则图书大厦CD 的高度为________米.17.如图,在△ABC 中,∠C =90°,AC =8,BC =6,点D 是AB 的中点,点E 在边AC 上,将△ADE 沿DE 翻折,使点A 落在点A′处,当A′E ⊥AC 时,A′B =____.18.如图,过锐角△ABC 的顶点A 作DE ∥BC ,AB 恰好平分∠DAC ,AF 平分∠EAC 交BC 的延长线于点F .在AF 上取点M ,使得AM=13AF ,连接CM 并延长交直线DE 于点H .若AC=2,△AMH 的面积是112,则1tan ACH ∠的值是_______.三、解答题19.计算:0112sin 45()2π--︒++.20.如图,为了求某条河的宽度,在它的对岸岸边任意取一点A ,再在河的这边沿河边取两点B 、C ,使得∠ABC=45°,∠ACB=30°,量得BC 的长为40m ,求河的宽度(结果保留根号).21.五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)22.如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,(1)求证:AC=BD;(2)若sinC=1213,BC=36,求AD的长.23.如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区,取MN上另一点B,测得BA方向为南偏东75°,已知MB=400m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?24.如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B 处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考≈1.41≈2.45)25.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:512,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长.(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75).26.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).27.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除.(参考≈1.414)参考答案1.A【分析】根据正弦的定义解答即可.【详解】∵在R t △ABC中,∠C = 90°,∴AB为斜边,BC为∠A所对直角边,∵∠A=α,∴sinα =BC AB,∴BC=AB sinα =2sinα,故选A.【点睛】本题考查三角函数的定义,在直角三角形中,正弦是锐角的对边与斜边的比;余弦是锐角的邻边与斜边的比;正切是锐角的对边与邻边的比;余切是锐角的邻边与对边的比;熟练掌握各三角函数的定义是解题关键.2.C【分析】根据勾股定理求出AB,并根据正弦公式:sinA=BCAB求解即可.【详解】∵∠C=90°,BC=3,AC=4∴5 AB=∴3 sin5BCAAB==故选C.【点睛】本题主要是正弦函数与勾股定理的简单应用,正确理解正弦求值公式即可.3.D【分析】过A作AB⊥x轴于点B,在Rt△AOB中,利用勾股定理求出OA,再根据正弦的定义即可求解.【详解】如图,过A作AB⊥x轴于点B,∵A的坐标为(4,3) ∴OB=4,AB=3,在Rt△AOB中,∴AB3 sin==OA5α故选:D.【点睛】本题考查求正弦值,利用坐标求出直角三角形的边长是解题的关键.4.B【分析】根据正弦的定义:正弦=对边/斜边即可解答.【详解】由题意得sinA=BCAB=1213,故选B.【点睛】掌握正弦公式是解答本题的关键.5.C【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.【详解】由题意,得 cosA=12,tanB=1,∴∠A=60°,∠B=45°,∴∠C=180°-∠A-∠B=180°-60°-45°=75°.故选C.6.A在直角△ABC中,根据勾股定理即可求得AB,而∠B=∠ACD,即可把求sin∠ACD转化为求sin B.【详解】在直角△ABC中,根据勾股定理可得:AB==3.∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,∴∠B=∠ACD,∴sin∠ACD=sin∠BAC==.AB故选A.【点睛】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系,难度适中.7.C【详解】试题分析:首先根据题意画出图形,由坡度为,可求得坡角∠A=30°,又由小明沿着坡度为600m,根据直角三角形中,30°所对的直角边是斜边的一半,即可求得答案解:如图,过点B作BE⊥AC于点E,∵坡度:i=1∴tan∠∴∠A=30°,=1000m,∴BE=1AB=300(m).2∴他升高了300m.故选C考点:解直角三角形的应用点评:此题考查了坡度坡角问题.此题比较简单,注意能构造直角三角形并用解直角三角形的知识求解是解此题的关键,注意数形结合思想的应8.A在直角三角形ADE 中,cosA=35=AE AB BEAD AD -= ,可以求得AB ,再利用勾股定理求得DE ,即可求得tan DEDBE BE∠= . 【详解】解:设菱形的边长为t2BE =2AE t ∴=-352AE AB BE t AD D tco A sA --==== 5t ∴=4DE ∴=4tan 22DE DBE BE ∴∠=== 故选A 【点睛】本题考查了菱形的性质和解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系. 9.D 【详解】试题解析:∵|sinA-12|+)2=0,∴|sinA-12|=0,-tanB )2=0,∴sinA-12=0-tanB=0,sinA=12,∴∠A=30°,∠B=30°, ∴∠C=120°. 故选D .考点:1.特殊角的三角函数值;2.非负数的性质:绝对值;3.非负数的性质:偶次方. 10.D 【分析】先计算对称轴为直线x=12,抛物线开口向下,可知A点为顶点(最高点),a最大;再根据B、C两点与对称轴的远近,比较纵坐标的大小.【详解】抛物线y=-x2+x+3的对称轴是直线x=12,开口向下,点A(12,a)为顶点,即最高点,所以,a最大,A、B错误;又1<sinα+cosα<2,-m2+2m-2=-(m-1)2-1≤-1,可知,B点离对称轴近,C点离对称轴远,由于抛物线开口向下,离对称轴越远,函数值越小,c<b,C错误;故选D.【点睛】比较抛物线上点的纵坐标大小,需要结合对称轴,开口方向,点与对称轴的远近,来比较大小.11.【详解】首先利用余弦函数的定义求得AC的长,然后利用勾股定理即可求得BC的长:∵△ABC中,∠C=90°,AB=8,,∴3AC AB cosA864=⋅=⨯=.∴BC=故答案为12.1 3【详解】解:作EF⊥BC于F,如图,设DE=CE=a,∵△CDE为等腰直角三角形,∴,∠DCE=45°,∵四边形ABCD为正方形,∴,∠BCD=90°,∴∠ECF=45°,∴△CEF为等腰直角三角形,∴,在Rt△BEF中,tan∠EBF=EFBF=13,即∠EBC=13.故答案为13.13.【详解】【分析】根据坡度等于坡角的正切值,以及正切的定义可设升高了xm,则水平距离为3xm,再根据勾股定理求得答案.【详解】设升高了xm,根据坡比为1:3,则可得水平距离为3xm,∴由勾股定理得x2+(3x)2=2002,解得故答案为.【点睛】本题考查了解直角三角形的应用,坡度坡角问题,熟练掌握坡比等于坡角的正切是解题的关键.14.β【分析】锐角三角函数值都是正值,余切值随着角度的增大(或减小)而减小(或增大).【详解】∵α、β是锐角,且cotα<cotβ,∴α>β,故α、β中较小的角是β.故答案为β.【点睛】考查了锐角三角函数的增减性.①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小);④余切值随着角度的增大(或减小)而减小(或增大).15.4 5 .【详解】试题分析:根据正切函数可设tanA=43=BCAC=43aa,根据勾股定理,可得AB=5a,再根据正弦函数可得sinA=BCAB=45aa=45.故答案为4 5 .考点:同角三角函数的关系.16.【分析】作DH⊥AB于H,根据正切的概念分别求出AB、AH,计算即可.【详解】作DH⊥AB于H,则DH=BC=30,在Rt△ADH中,AH=DH×tanα=10 ,在Rt △ABC 中,AB=BC tan30︒ =30 ,则CD=AB ﹣AH=20(米),故答案为20. 【点睛】 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.17【分析】分两种情况:①如图1, 作辅助线, 构建矩形, 先由勾股定理求斜边AB=10, 由中点的定义求出AD 和BD 的长, 证明四边形HFGB 是矩形, 根据同角的三角函数列式可以求DG 和DF 的长,并由翻折的性质得: ∠DA' E=∠A,A' D=AD=5, 由矩形性质和勾股定理可以得出结论②如图2, 作辅助线, 构建矩形A' MNF,同理可以求出A' B 的长.【详解】解:分两种情况:如图1,过D 作DG ⊥BC 与G, 交A' E 与F, 过B 作BH ⊥A' E 与H,D 为AB 的中点,∴BD=12AB=AD,∠C=90o ,AC=8,BC=6,∴AB=10,∴BD=AD=5, sin ∠ABC=DG AC BD AB =,8510DG ∴= ∴DG=4, 由翻折得: ∠DA' E=∠A, A' D=AD=5,∴sin ∠DA' E=sin ∠A=BC DF AB A D='.∴6105DFA=∴DF=3,∴FG=4-3=1,A'E⊥AC,BC⊥AC,∴A'E//BC,∴∠HFG+∠DGB=180o,∠DGB=90o,∴∠HFG=90o,∴∠EHB=90o,∴四边形HFGB是矩形,∴BH=FG=1,同理得: A' E=AE=8 -1=7,∴A'H=A'E-EH=7-6=1,在Rt△AHB中, 由勾股定理得如图2,过D作MN//AC, 交BC与于N,过A' 作A' F//AC, 交BC的延长线于F,延长A' E交直线DN 于M, A'E⊥AC,∴A' M⊥MN, A' E⊥A'F,∴∠M=∠MA'F=90o,∠ACB=90o,∴∠F=∠ACB=90o,∴四边形MA' FN県矩形,∴MN=A'F,FN=A'M,由翻折得: A' D=AD=5,Rt△A'MD中,DM=3,A'M=4,∴FN=A'M=4,Rt△BDN中,BD=5,∴DN=4, BN=3,A' F=MN=DM+DN=3+4=7,BF=BN+FN=3+4=7,Rt△ABF中, 由勾股定理得=综上所述,A'B故答案为或【点睛】本题主要考查三角形翻转后的性质,注意不同的情况需分情况讨论.18..【详解】试题分析:过点H作HG⊥AC于点G,∵AF平分∠CAE,DE∥BF,∴∠HAF=∠AFC=∠CAF,∴AC=CF=2,∵AM=AF,∴,∵DE∥CF,∴△AHM∽△FCM,∴,∴AH=1,设△AHM中,AH边上的高为m,△FCM中CF边上的高为n,∴=,∵△AMH的面积为:,∴=AH•m∴m=,∴n=,设△AHC的面积为S,∴=3,∴S=3S△AHM=,∴AC•HG=,∴HG=,∴由勾股定理可知:AG=,∴CG=AC﹣AG=2﹣,∴==.故答案为.考点:相似三角形的判定与性质;解直角三角形;综合题.19.3.【详解】试题分析:根据二次根式、绝对值意义、特殊角的三角函数值、零指数幂法则、负整数指数幂法则计算即可得到结果.试题解析:原式=212-+=3.考点:1.实数的运算;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.20.20)m .【分析】如图,过A 作AD ⊥BC 于D ,设AD =x m ,通过锐角三角函数可知:BD =x m ,DC m ;根据BC 的长为40m 即可建立方程,解之即可求出河宽.【详解】解:作AD ⊥BC,垂足为D .设AD = x m ,∵∠ABC =45°,∴BD =AD = x m ,∵∠ACB =30°,∴DC =tan 30AD︒m ,∵AD+DC=BC ,且BC =40m ,∴40x =,解得,20x =,答:则河的宽度为20)m.【点睛】本题主要考查解直角三角形的实际应用. 通过添加辅助线构造直角三角形是解题的关键. 21.AB=2.88千米.【详解】试题分析:作OC ⊥AB .在在Rt △AOC 中,求出AC 、OC 的长,从而求出BC 的长,于是将AC 、BC 相加即可.试题解析:作OC ⊥AB .∵AB ∥OF ,∴∠A=72°,∠B=40°,∴在Rt△AOC中,AC=2×cos72°≈2×0.31=0.62(千米),OC=2×sin72°≈2×0.95=1.9(千米),在Rt△BOC中,=tan40°,即≈0.84,BC≈=2.26(千米),∴AB=0.62+2.26=2.88(千米).点睛:本题考查了方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.22.(1)证明见解析(2)8【分析】(1)由于tan B=cos∠DAC,所以根据正切和余弦的概念证明AC=BD;(2)设AD=12k,AC=13k,然后利用题目已知条件解直角三角形即可.【详解】解:(1)∵AD是BC上的高,∴AD⊥BC,∴∠ADB=90°,∠ADC=90°.在Rt△ABD和Rt△ADC中,∵tan B=ADBD,cos∠DAC=ADAC,tan B=cos∠DAC,∴ADBD=ADAC,∴AC=BD.(2)在Rt△ADC中,sin C=1213,故可设AD=12k,AC=13k,∴CD k,∵BC=BD+CD,AC=BD,∴BC=13k+5k=18k.由已知BC=12,∴18k=12,∴k=23,∴AD=12k=12×23=8.点睛:此题考查解直角三角形、直角三角形的性质等知识,也考查逻辑推理能力和运算能力.23.如果不改变方向,输水路线不会穿过居民区【分析】问输水线路是否会穿过居民区,其实就是求A到MN的距离是否大于圆形居民区的半径,如果大于则不会穿过,反之则会.【详解】作AC⊥MN于点C,∵∠AMC=60°-30°=30°,∠ABC=75°-30°=45°,∴设AC为xm,则AC=BC=x,在Rt△ACM中,MC=400+x,∴tan∠AMC=,即=,解得x =200+200>500,∴如果不改变方向,输水路线不会穿过居民区.【点睛】本题考查了解直角三角形的应用,当两个直角三角形有公共的直角边时,利用这条公共边来求解是解决此类题目的基本出发点.24.小岛A与小岛B之间的距离是100km.【分析】先过点C作CP⊥AB于P,根据已知条件求出∠PCB=∠PBC=45°,∠CAP=60°,再根据轮船的速度和航行的时间求出BC的值,在Rt△PCB中,根据勾股定理求出BP=CP的值,再根据特殊角的三角函数值求出AP的值,最后根据AB=AP+PB,即可求出答案.【详解】解:过点C作CP⊥AB于P,∵∠BCF=45°,∠ACE=60°,AB∥EF,∴∠PCB=∠PBC=45°,∠CAP=60°,∵轮船的速度是45km/h ,轮船航行2小时,∴BC=90,∵BC2=BP2+CP2,∴∵∠CAP=60°,∴tan60°=CP AP∴,∴(km ).答:小岛A 与小岛B 之间的距离是100km .【点睛】本题考查解直角三角形的应用-方向角问题.25.(1)改造前坡顶与地面的距离BE 为24米;(2)BF 至少是8米【详解】整体分析:(1)Rt △ABE 中,根据斜坡AB 的坡比为i=1:512,且AB=26米解直角三角形;(2)过点F 作FG ⊥AD 于点G ,用∠FAG 的余切求出AG 即可.解:(1)在Rt △ABE 中,AB=26,i=BE AE =125, 设BE=12k ,AE=5k ,则AB=13k=26,k=2,∴AE=10(米),BE=24(米);(2)过点F 作FG ⊥AD 于点G ,由题意可知:FG=BE=24,∠FAD=53°,在Rt △AFG 中,cot53°=24AG =0.75, ∴AG=18, ∴BF=GE=AG ﹣AE=8米,答:改造前坡顶与地面的距离BE 为24米;BF 至少是8米.26.拦截点D 处到公路的距离是(500+)米.【详解】试题分析:过B 作AB 的垂线,过C 作AB 的平行线,两线交于点E ;过C 作AB 的垂线,过D 作AB 的平行线,两线交于点F ,则∠E=∠F=90°,拦截点D 处到公路的距离DA=BE+CF .解Rt △BCE ,求出BE=BC=×1000=500米;解Rt △CDF ,求出CF=CD=500米,则DA=BE+CF=(500+500)米.试题解析:如图,过B 作AB 的垂线,过C 作AB 的平行线,两线交于点E ;过C 作AB 的垂线,过D 作AB 的平行线,两线交于点F ,则∠E=∠F=90°,拦截点D 处到公路的距离DA=BE+CF .在Rt △BCE 中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE=BC=×1000=500米;在Rt △CDF 中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF=CD=500米,∴DA=BE+CF=(500+500)米,故拦截点D 处到公路的距离是(500+500)米.考点:解直角三角形的应用-方向角问题.27.需要拆除.【分析】由题意得到△ABC为等腰直角三角形,求出AB的长,在Rt△BCD中,根据新坡面的坡度求出∠BDC=30°,得到DC的长,再利用勾股定理求出DB的长,由DB﹣AB求出AD的长,再比较AD+3与10的大小即可.【详解】解:需要拆除,理由为:∵CB⊥AB,∠CAB=45°,∴△ABC为等腰直角三角形,∴AB=BC=10米,在Rt△BCD中,新坡面DC的坡度为3,即∠CDB=30°,∴DC=2BC=20米,=∴AD=BD﹣AB=(10)米≈7.32米,∵3+7.32=10.32>10,∴需要拆除.【点睛】本题考查解直角三角形的应用-坡度坡角问题;属于应用题.。

第四章单元检测卷[时间:90分钟分值:150分]一、选择题(每小题4分,共40分)1.如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是()A.513 B.1213 C.512 D.1352.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m,线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放风筝()A.甲的最高B.乙的最高C.丙的最高D.乙的最低3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=6,BC=2,则sin∠ACD的值为()A.155 B.255 C.52 D.62第3题图第4题图4.如图,△ABC的顶点是正方形网格的格点,则sin B的值为()A.12 B.22 C.32D.15.在Rt△ABC中,∠C=90°,已知cos A=35,那么tan A等于()A.43 B.34 C.45 D.546.如图,为测量河两岸相对的两电线杆A,B之间的距离,在距A点16 m 的C处(AC⊥AB)测得∠ACB=52°,则A,B两点间的距离为()A.16sin 52° m B.16cos 52°m C.16tan 52° m D.16tan 52°m 7.如图,在水平地面上,由点A测得旗杆BC顶点C的仰角为60°,点A 到旗杆的距离AB=12 m,则旗杆的高度为()A.6 3 m B.6 m C.12 3 m D.12 m第7题图第8题图8.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A 处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是()A.2海里B.2sin 55°海里C.2cos 55°海里D.2tan 55°海里9.若α,β都是锐角,且cos α>cos β,则下列式子正确的是()A.α>βB.sin α<sin βC.tan α>tan βD.以上式子都不正确10.如图,在△ABC中,AD⊥BC,垂足为点D,若AC=62,∠C=45°,tan ∠ABC=3,则BD等于()A.2 B.3 C.3 2 D.2 3二、填空题(每小题4分,共32分)11.计算:cos2 45°+tan 30°·sin 60°=_______.12.在△ABC中,∠C=90°,AB=10,BC=6,则sin A=________,tan B=___________.13.如图所示,河堤横断面迎水坡AB的坡比(指坡面的铅直高度BC与水平宽度CA的比)是1∶3,堤高BC=5 m,则坡面AB的长度是_________m.14.如图,已知Rt△ABC中,斜边BC上的高AD=4,cos B=45,则AC=________.15.在Rt△ABC中,∠C=90°,cos B=32,a=3,那么b=______.16.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC,AB于点D,E.如果BC=8,tan A=43,那么BD=________.,)17.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_________海里.,第17题图),第18题图) 18.如图,是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6米,斜坡AB的坡比为1∶2.4,现把图中的货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过________米.三、解答题(共7小题,满分78分)19.(10分)计算:32sin 60°-2cos 45°-33tan 30°·cos 60°.20.(10分)如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫作角α的余切,记作cot α=角α的邻边角α的对边=ACBC.根据上述角的余切的定义,解答下列问题:(1)cot 30°=___________;(5分)(2)如图,已知tan A=34,其中∠A为锐角,试求cot A的值.21.(10分)如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5 m的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22 m,求旗杆CD的高度.(结果精确到0.1,参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)22.(10分)如图,在△ABC中,AD是BC边上的高,∠C=45°,sin B=1 3,AD=1,求BC的长.23.(12分)某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚好在南海巡航的渔政船前往救援.当飞机到达距离海面3 000 m的高空C处时,测得A处渔政船的俯角为60°,测得B处发生险情的渔船的俯角为30°,请问此时渔政船和渔船相距多远?(结果保留根号)24.(12分)如图,AD是△ABC的中线,tan B=13,cos C=22,AC= 2.求:(1)BC的长;(2)sin∠ADC的值.25.(14分)如图所示,建筑物AB后有一座假山,其坡度为i=1∶3,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.参考答案[时间:90分钟分值:150分]一、选择题(每小题4分,共40分)1.A2.B3.A4.B 5.A 6.C7.C 8.C9.B 10.A【解析】∵AC=62,∠C=45°,AD⊥BC,∴AD=AC·sin 45°=62×22=6.∵tan ∠ABC=3,∴ADBD=3,∴BD=AD3=2.二、填空题(每小题4分,共32分)11.1 12.354313.1014.5【解析】∵△ABC为直角三角形,AD⊥BC于点D,∴∠BAD+∠CAD=90°,∠B+∠BAD=90°,∴∠CAD=∠B,∴cos B=cos ∠CAD=ADAC=45.又∵AD=4,∴AC=5.15.1 16.25 417.10 3【解析】根据题意可知∠CAD=30°,∠CBD=60°. ∵∠CBD=∠CAD+∠ACB,∴∠CAD=∠ACB=30°,∴AB=BC=20海里.在Rt△CBD中,∠BDC=90°,∠CBD=60°,∴sin 60°=CD BC,∴CD=BC·sin 60°=20×32=103海里.18.2.4三、解答题(共7小题,满分78分)19.解:原式=32×32-2×22-33×33×12(4分)=34-1-16(8分)=-512.(10分)20(1) 3解:(2)∵tan A=BCAC=34,∴cot A=ACBC=43.(10分)21.解:在Rt△DEB中,∠DEB=90°,BE=AC=22 m,tan 32°=DE BE,(5分)∴DE=BE·tan 32°≈22×0.62=13.64(m).(8分) ∵CE=AB=1.5 m,∴CD=CE+DE≈1.5+13.64≈15.1(m).答:旗杆CD的高度约为15.1 m.(10分)22.解:在Rt△ABD中,∵AD=1,∴sin B=ADAB=13,∴AB=3,(4分)∴BD=AB2-AD2=2 2.(6分)在Rt△ADC中,∵∠C=45°,∴CD=AD=1,(8分)∴BC=BD+CD=22+1.(10分)23.解:在Rt△CDA中,∠ACD=30°,CD=3 000 m,∴AD=CD·tan∠ACD=1 000 3 m.(4分)在Rt△CDB中,∠BCD=60°,∴BD=CD·tan∠BCD=3 000 3 m,(8分)∴AB=BD-AD=2 000 3 m.答:此时渔政船和渔船相距2 000 3 m.(12分)24.答图解:(1)如答图,过点A作AE⊥BC于点E.∵cos C=22,∴∠C=45°.(1分)在Rt△ACE中,CE=AC·cos C=1,∴AE=CE=1.(3分)在Rt△ABE中,tan B=13,即AEBE=13,∴BE=3AE=3,(5分)∴BC=BE+CE=4.(6分) (2)∵AD是△ABC的中线,∴CD=12BC=2,∴DE=CD-CE=1.(8分)∵AE⊥BC,DE=AE,∴∠ADC=45°,(10分)∴sin∠ADC=22.(12分)25.答图解:如答图,过点E作EF⊥BC于点F,EN⊥AB于点N.(2分) ∵假山的坡度为i=1∶3,∴设EF=x米,则FC=3x米.(4分)∵CE=20米,∴x2+(3x)2=400,解得x=10,则FC=103米.(8分)∵BC=25米,∴BF=NE=(25+103)米.(10分)∵∠AEN=45°,∴AN=EN=(25+103)米,(12分)∴AB=AN+BN=NE+EF=25+103+10=(35+103)米.答:建筑物AB的高为(35+103)米.(14分)。
第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如果,那么的范围是()A. B. C. D.2、如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为()A. B. C. D.3、在Rt△ABC中,已知∠B=90°,AC=10,AB=5,则∠A等于()A.45°B.30°C.60°D.50°4、sin30°的值等于()A. B. C. D.15、如图,已知点A(-1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有()A.2个B.3个C.6个D.7个6、如图1是一个手机的支架,由底座、连杆和托架组成(连杆始终在同一平面内),垂直于底座且长度为的长度为的长度可以伸缩调整.如图2,保持不变,转动,使得,假如时为最佳视线状态,则此时的长度为(参考数据:)()A. B. C. D.7、如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是()A. B. C. D.8、在Rt△ABC中,∠C=90°,a=4,b=3,则sinA的值是()A. B. C. D.9、在Rt△ABC中,∠C=90°,BC=4,sinA= ,则AB的长为()A. B.6 C.12 D.810、如图,▱ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )A.﹣4tanαB.﹣2sinαC.﹣4cosαD.﹣2tan11、如图,在RtΔABC中,∠C=90°,∠A=30°, E为AB上一点,且AE︰EB=4︰1,EF ⊥AC于F,连结FB,则tan∠CFB的值等于()A. B. C. D.12、在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA等于()A. B. C. D.13、在Rt△ABC中,∠ACB=90°,BC=1,AC=2,则下列结论正确的是()A.sinA=B.tanA=C.cosB=D.tanB=14、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B.C.D.15、如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为(用含α的代数式表示()A.7sin 米B.7cos 米C.7tan 米D. 米二、填空题(共10题,共计30分)16、如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为________。
湘教版九年级上册数学第4章锐角三角函数含答案一、单选题(共15题,共计45分)1、西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表。
如图是一个根据北京的地理位置设计的圭表,其中,立柱的高为。
已知,冬至时北京的正午日光入射角约为,则立柱根部与圭表的冬至线的距离(即的长)作为()A. B. C. D.2、在正方形网格中,△ABC的位置如图所示,则cosB的值为()A. B. C. D.3、如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于,则sin∠CAB=()A. B. C. D.4、如图,某建筑物上挂着“巴山渝水,魅力重庆”的宣传条幅,王同学利用测倾器在斜坡的底部处测得条幅底部的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡的坡度米,米(点在同平面内,,测倾器的高度忽略不计),则条幅的长度约为()(参考数据:)A.12.5米B.12.8米C.13.1米D.13.4米5、在正方形网格中,如图放置,则等于()A. B. C. D.6、如图所示,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )A. B. C. D.7、如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为()A.16B.16C.20D.208、如图,直线y=x+3与x、y轴分别交于A、B两点,则cos∠BAO的值是( )A. B. C. D.9、若∠A为锐角,且cosA<0.5,则∠A()A.小于30°B.大于30°C.大于60°D.大于60°10、在正方形网格中,∠α的位置如图所示,则tanα的值是()A. B. C. D.211、如图,的三个项点均在格点上,则的值为()A. B. C.2 D.12、勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB(图2).若AD=,tan∠AON=,则正方形MNUV的周长为()A. B.18 C.16 D.13、下列选项错误的是()A. B. C. D.14、如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C 处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是()A.20海里B.40海里C. 海里D. 海里15、在直角三角形中,各边的长度都扩大到原来的3倍,则锐角A的三角函数值()A.都扩大到原来的3倍B.都缩小为原来的3倍C.都保持原来的数值都不变D.有的变大,有的缩小二、填空题(共10题,共计30分)16、如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C 在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为________.17、△ABC中,∠C=90°,AB=8,cosA=,则BC的长________18、如图,把两张宽度都是3cm的纸条交错的叠在一起,相交成角α.则重叠部分的面积为________.19、小颖家住在甲楼,她所居住的楼房前面有一座乙楼。
第4章过关自测卷(90分钟 100分)一.选择题(每题3分,共30分)1.图1,P 是角α的边OA 上一点,点P 的坐标为(12,5),则tanα等于( ) A.135 B.1312 C.125 D.512图1 图2 图32.在直角三角形ABC 中,各边的长度都扩大为原来的2倍,那么锐角A 的正弦值.余弦值和正切值( )A.都扩大为原来的2倍B.都缩小为原来的21C.都不变D.无法确定3.已知在Rt △ABC 中,∠C=90°,AC =BC ,点D 在AC 上,∠CBD =30°,则DC AD 的值为( ) A.3 B.22 C. 3-1 D.不能确定 4.1,则菱形的四个角分别为( )A.30°.150°.30°.150°B.45°.135°.45°.135°C.60°.120°.60°.120°D.不能确定5.如图2,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m .如果在坡度为0.75的山坡上种树,也要求株距为4 m ,那么相邻两树间的坡面距离为( )A.5 mB.6 mC.7 mD.8 m6.已知∠A ,∠B 是Rt △ABC 的两个锐角,则方程tanA ·x ²-2x +tanB =0( )A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.根的情况无法确定7.如图3,一艘轮船由海平面上A 地出发向南偏西40°的方向行驶40 n mile 到达B 地,再由B 地向北偏西20°的方向行驶20 n mile 到达C 地,则A ,C 两地相距( )A.30 n mileB.40 n mileC.203 n mileD.103 n mile8.如图4,某水库堤坝横断面迎水坡AB 的坡度i =1BC=50 m ,则迎水坡面AB 的长度是( ) A.100 m B.1003 m C.150 m D.503m图4 图5 图69.如图5所示,学校的保管室里,有一架5 m 长的梯子OC 斜靠在墙上,此时梯子OC 与地面所成的角为45°,如果梯子底端O 固定不动,顶端C 靠到对面墙上的C ′点,此时梯子OC ′与地面所成的角为60°,则此保管室的宽度AB 为( ) A.25(2+1)m B.25(3+2)mC.32mD.25(3+1)m 10.(2013,广州)如图6所示,四边形ABCD 是梯形,AD ∥BC ,CA 是∠BCD 的平分线,且AB ⊥AC ,AB =4,AD =6,则tanB 等于( ) A.23 B.22 C.411 D.55 二.填空题(每题3分,共24分)11.计算:cos 245°+tan 30°·sin 60°=________.12.在△ABC 中,∠A ,∠B 都是锐角,且(cosA -21)²+|1-tanB |=0,则∠C =__________.13.若tanα=5,则ααααcos 3sin 2cos -sin +=__________. 14.如图7,孔明同学背着一桶水,从山脚A 出发,沿与地面成30°角的山坡向上走,送水到山上因春季受旱缺水的王奶奶家(B 处),AB =80 m ,则孔明从A 到B 上升的高度BC 是________m .图7 图8 图9 图1015.如图8,△ABC 中,∠B =30°,∠A =15°,若BC 边上的高为2,则BC =__________.16.在△ABC 中,∠A ,∠B 都是锐角,且sinA =21,tanB =3,AB =10,则△ABC 的面积为___________.17.全市动员修海堤抗台风,某海堤的横断面是梯形,如图9所示,迎水坡BC 的坡角为30°,背水坡AD 的坡度i =1∶1.2,堤顶宽DC为3 m,堤高DF为10 m,则堤底宽AB约为________m.(精确到0.1 m)18.如图10,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=53,则DE=________. 三.解答题(19题4分,20题6分,24题8分,其余每题7分,共46分)19.(1)计算:121-⎪⎭⎫⎝⎛+8+|1-2|0-2sin60°·tan60°;(2)计算:sin²30°+cos²45°+2sin60°·tan45°.20.小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图11所示).小船从P处出发,沿北偏东60°方向划行200 m到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1 m)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,2≈1.41,3≈1.73)图1121.小明将一副三角尺如图12所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD=2,求AC的长.图1222.在一次综合实践活动中,小明要测某地一座古塔AE的高度,如图13,已知塔基AB的高为4 m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5 m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)(1)求AC的距离;(结果保留根号)(2)求塔高AE.(参考数据:tan50°≈1.2,sin50°≈0.77,cos50°≈0.64,3≈1.73,2≈1.41,结果保留整数)图13 23.如图14,一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10 n mile到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离.(2≈1.4, 3≈1.7,结果保留整数)图1424.某过街天桥的截面图为梯形,如图15所示,其中天桥斜面CD 的坡度i =1∶3,CD 的长为10 m ,天桥另一斜面AB 的坡角∠ABG =︒45.(1)求过街天桥斜面AB 的坡度;(2)求DE 的长;(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF ,试计算此改建需占路面的宽度FB .(结果精确到0.01 m )图1525.阅读下列材料,并解决后面的问题.如图16所示,在锐角三角形ABC 中,设∠BAC ,∠B ,∠C 的对边分别是a ,b ,c .过点A 作AD ⊥BC 于点D ,则sinB =c AD ,sinC =bAD ,即AD =c ·sinB ,AD =b ·sinC .于是c ·sinB =b ·sinC ,即C c B b sin sin =,同理有,sin sin sin sin B b BAC a BAC a C c =∠∠=,所以C c B b BAC a sin sin sin ==∠. 即:在一个锐角三角形中,各边和它所对角的正弦的比相等.图16(1)在锐角三角形中,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,若已知三个元素,a ,b ,∠A ,运用上述结论和有关定理就可以求出其余三个未知元素c ,∠B ,∠C .请你按照下列步骤填空,完成求解过程.第一步:由a ,b ,∠A −−−→−用关系式__________求出∠B ; 第二步:由∠A ,∠B −−−→−用关系式__________求出∠C ; 第三步:由__________−−−→−用关系式__________求出c ; (2)一货轮在C 处测得灯塔A 在货轮北偏西30°方向上,随后货轮以28.4 n mile /h 的速度按北偏东45°的方向航行,0.5 h 后到达B 处, 此时又测得灯塔A 在货轮的北偏西70°方向上(如图17所示),利用上面的结论求此时货轮到灯塔A 的距离AB .(结果精确到0.1 n mile ,参考数据:sin 40°≈0.643,sin 65°≈0.906,sin 70°≈0.940,sin 75°≈0.966)图17参考答案及点拨一.1.C 2.C 3.C4.C 点拨:设较大内角为α,则tan 2α =3,所以2α=60°,所以α=120°.5.A6.B 点拨:因为b 2-4ac =(-2)2-4·tanA ·tanB =4-4×1=0,故方程有两个相等的实数根.7.C 8.A 9.A10.B 点拨:过点D 作AB 的平行线交AC 于点E ,交BC 于点F ,如答图1,易知四边形ABFD 是平行四边形,∴BF =AD =6,DF =AB =4,∵AB ⊥AC ,DF ∥AB ,∴DF ⊥AC ,又∵CA 是∠BCD 的平分线,∴CD =CF ,∠DCA =∠ACB ,又∵AD ∥BC ,∴∠DAC =∠ACB ,∴∠DAC =∠DCA .∴DC =DA =6,∴CF =6,∴BC =BF +CF =12.易求得AC =82,∴tanB =AB AC =428=22. 答图1二.11.1 点拨:cos 245°+tan 30°·sin 60°=222⎪⎪⎭⎫ ⎝⎛+33×23=21+21=1. 12.75° 13.83 点拨:原式=3cos sin 2cos sin +-αααα=3tan 2tan +-αα=3525+-=83.14.40 15.32-2 点拨:设BC 边上的高为AD ,由题意知,AD =2,∠ACD =∠B +∠BAC =45°,∴tan 45°=CD AD =CD 2=1,∴CD =2, ∴tan B =BD AD =22-BC =33,解得BC =23-2. 16.2325 点拨:在该题中,并没有直接指明△ABC 是直角三角形,所以需先判断其为直角三角形,然后才能利用解直角三角形的知识解题.17.32.3 18.415 点拨:由题易证△AED ∽△ABC ,在△ABC 中,BC =6,sin A =53,可求得AB =10,AC =8.利用相似三角形的性质可求得DE 的长. 三.19.解:(1)原式=2+22+1-2×23×3=2+22+1-3=22. (2)原式=221⎪⎭⎫ ⎝⎛+222⎪⎪⎭⎫ ⎝⎛+2×23×1=41+21+26=43+26. 20.解:过P 作PC ⊥AB 于C ,如答图2,在Rt △APC 中,AP =200 m ,∠ACP =︒90,∠PAC =60°.∴PC =200×sin 60°=200×23=1003(m ).∵在Rt △PBC 中,sin ︒37=PB PC ,∴PB =︒37sin PC ≈6.073.1100⨯≈288(m ).答:这时小亮与妈妈相距约288 m .答图221.解:在Rt △BCD 中,∠BCD =45°,CD =2,cos ∠BCD =BC CD ,∴BC = BCD CD ∠cos =︒45cos 2=22.在Rt △ABC 中,∠BAC =60°,sin ∠BAC =AC BC ,∴AC =BAC BC ∠sin =︒60sin 22=2322=364.∴AC 的长为364. 点拨:△ABC 和△BCD 都是有特殊锐角的直角三角形,所以利用特殊角的三角函数值便可求得AC 的长.22.解:(1)在Rt △ABC 中,AB =4 m ,∠BCA =30°,由tan ∠BCA =ACAB ,得AC =BCA AB ∠tan =︒30tan 4=334=43(m ). ∴AC 的距离为43 m .(2)设AE=x m ,在Rt △AED 中,由tan 50°=ADx ,得AD =︒tan50x ≈1.2x (m ),∵CD =AD -AC =5,∴1.2x -43≈5,解得x ≈14, ∴塔高AE 约为14m .23.解:由题意知:∠BAC =53°-23°=30°,∠C =23°+22°=45°.过点B 作BD ⊥AC ,垂足为D ,则CD =BD .∵BC =10 n mile ,∴CD =BD =BC ·cos 45°=10×22=52 (n mile ),∴AD =325332530tan ⨯==︒BD ≈5×1.4×1.7=11.9(nmile ).∴AC =AD +CD ≈11.9+25≈11.9+7.0=18.9≈19(n mile ). 答:此时小船与码头之间的距离约为19 n mile .24.解:(1)在Rt △AGB 中,∠ABG =45°,所以AG =BG .所以AB 的坡度为AG ∶BG =1∶1.(2)在Rt △DEC 中,tanC =33=EC DE ,所以∠C =30°.又因为CD =10 m , 所以DE =CD ·sin 30°=5 m .(3)由(1)(2)知,AG =BG =DE =5 m ,在Rt △AFG 中,∠AFG =30°,tan ∠AFG =FGAG ,即5533-=FB .所以FB =35-5≈3.66 (m ). 答:此改建需占路面的宽度FB 约为3.66 m .25.解:(1)Bb A a sin sin =;∠A +∠B +∠C =180°;a ,∠A ,∠C ;Cc A a sin sin = (2)根据题意,得∠ABC =180°-45°-70°=65°,∠A =180°-(30°+45°+65°)=40°,BC =0.5×28.4=14.2(n mile ).因为︒=︒40sin 2.1475sin AB ,所以AB ≈643.0966.02.14⨯≈21.3(n mile ),所以此时货轮到灯塔A 的距离AB 约为21.3。
湘教版九年级上册数学第4章锐角三角函数含答案一、单选题(共15题,共计45分)1、如图,河坝横断面迎水坡的坡比是(坡比是坡面的铅直高度与水平宽度之比),坝高,则坡面的长度是().A. B. C. D.2、如图,AB是⊙O的弦,OC⊥AB于点H,若∠AOC=60°,OH=1,则弦AB的长为()A.2B.C.2D.43、如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为()(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)A.20mB.15mC.12mD.16m4、如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosA的是()A. B. C. D.5、在Rt△ABC中,∠C=90°,cos A=,则tan A等于()A.2B.C.D.246、如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为.若在坡比为的山坡树,也要求株距为,那么相邻两棵树间的坡面距离()A. B. C. D.7、在△ABC中,∠C=90°,AB=10,cosA=,则BC的长为()A.6B.7.5C.8D.12.58、如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是()A. 米2B. 米2C. 米2 D. 米29、如图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则sin∠EAB的值为()A. B. C. D.10、在Rt△ABC中,∠C=90°,BC=4,AC=3,则cosA的值是()A. B. C. D.11、在中,,,若,则的长为().A. B. C. D.12、如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinA的值越小,梯子越陡B.cosA的值越小,梯子越陡C.tanA 的值越小,梯子越陡D.陡缓程度与∠A的函数值无关13、在平面直角坐标系xOy中,点A在直线上l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E,给出如下定义:若线段OE,⊙A和直线1上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B.C,D顺时针排列),则称矩形ABCD为直线的“理想矩形.例如,图中的矩形ABCD为直线1的“理想矩形”,若点A(3,4),则直线y=kx+1(k≠0)的“理想矩形”的面积为()A.12B.3C.4D.314、如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是()A.tan55°=B.tan55°=C.s in55°=D.cos55°=15、如图⊙O的半径为5,弦AB=,C是圆上一点,则∠ACB的度数是()A.30°B.45°C.60°D.90°二、填空题(共10题,共计30分)16、如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是________.17、一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B处,测得灯塔P在它的东北方向,若灯塔P正南方向4海里的C处是港口,点A,B,C在一条直线上,则这艘货轮由A到B航行的路程为________海里(结果保留根号).18、我们知道,四边形不具有稳定性,容易变形.一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把的值叫做这个平行四边形的变形度.如图,矩形ABCD的面积为5,如果变形后的平行四边形A1B1C1D1的面积为3,那么这个平行四边形的变形度为________.19、如图,方格纸中的每个小方格都是边长为1个单位长度的张方形,每个小正方形的顶点叫各点△ABC的顶点都在方格的格点上,则cosA=________.20、如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,OE=3,∠ABC=60°,则BD=________.21、一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为________海里/小时.22、如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan (α+β)________ tanα+tanβ.(填“>”“=”“<”)23、如图,在Rt△ABC中,∠C=90°,AB= 5,AC= 4,则cosA=________.24、已知均为锐角,且满足I sina- I+ =0,则=________.25、如图Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,E为⊙O上一点,连结CE,过C作CD⊥CE,交BE于点D,已知tanA=,AB=2 ,DE=5,则tan∠ACE=________.三、解答题(共5题,共计25分)26、计算:÷ +8×2﹣1﹣(+1)0+2•sin60°.27、第十一届全国少数民族传统体育运动会于9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会,其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°,此时,两人的水平距离EC为4m,已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.(参考数据:sin53°≈ ,cos53°≈ ,tan53°≈ )28、已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP//AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.(1)求证:△ADE∽△ACB;(2)设CD=x,tan BAE = y,求y关于x的函数解析式,并写出它的定义域;(3)如果△COD与△BEA相似,求CD的值.29、如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,(1)求证:CB//PD;(2)若AB=5,sin∠P=,求BC的长.30、如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:≈1.414,≈1.732)参考答案一、单选题(共15题,共计45分)1、B2、A4、A5、A6、C7、A8、C9、B10、B11、A12、B13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、。
第4章检测题
时间:120分钟 满分:120分
一、选择题(本大题共10个小题,每小题3分,共30分)
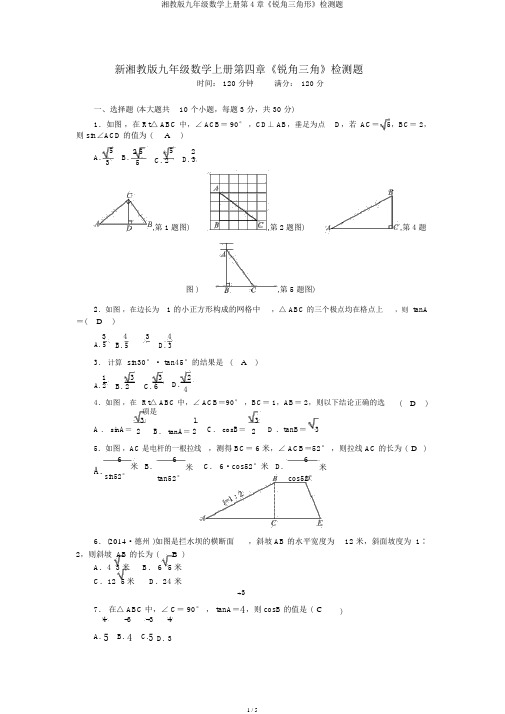
1.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为点D ,若AC =5,BC =2,则sin ∠ACD 的值为( A )
A.
53 B.255 C.52 D.23
,第1题图) ,第2题图) ,第4题
图) ,第5题图)
2.如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,则tan A =( D )
A.35
B.45
C.34
D.43
3.计算sin30°·tan45°的结果是( A ) A.12 B.32 C.36 D.24
4.如图,在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是( D ) A .sin A =
32 B .tan A =12 C .cos B =3
2
D .tan B = 3 5.如图,AC 是电杆的一根拉线,测得BC =6米,∠ACB =52°,则拉线AC 的长为( D ) A.6sin52°米 B.6tan52°米 C .6·cos52°米 D.6
cos52°
米
6.(2014·德州)如图是拦水坝的横断面,斜坡AB 的水平宽度为12米,斜面坡度为1∶2,则斜坡AB 的长为( B )
A .43米
B .65米
C .125米
D .24米
7.在△ABC 中,∠C =90°,tan A =3
4,则cos B 的值是( C )
A.45
B.34
C.35
D.43
8.如图,渔船在A 处看到灯塔C 在北偏东60°方向上,渔船向正东方向航行了12海里到达B 处,在B 处看到灯塔C 在正北方向上,这时渔船与灯塔C 的距离是( D ) A .123海里 B .63海里 C .6海里 D .43海里 9.如图,为测量B 点到河岸AD 的距离,在A 点测得∠BAD =30°,在C 点测得∠BCD =60°,又测得AC =100米,则B 点到河岸AD 的距离为( B )
A .100米
B .503米 C.2003
3
米 D .50米
,第9题图) ,第10题图)
10.(2014·深圳)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( B )
A .(600-2503)米
B .(6003-250)米
C .(350+3503)米
D .5003米
二、填空题(本大题共8个小题,每小题3分,共24分)
11.在Rt △ABC 中,∠C =90°,如果AC =3,AB =5,那么cos B 的值是__4
5__.
12.在△ABC 中,∠C =90°,BC =2,sin A =2
3
,则AC 的长是__5__.
13.如图,在地面上的点A 处测得树顶B 的仰角为α度,AC =7米,则树高BC 为__7tan α__米.(用含α的代数式表示)
,第13题图) ,第14题图) ,第16题图)
,第17题图)
14.如图,△ABC 中,∠C =90°,BC =4 cm ,tan B =3
2
,则△ABC 的面积是__12__cm 2.
15.在△ABC 中,若∠A ,∠B 满足|cos A -12|+(sin B -2
2)2=0,则∠C =__75°__.
16.长为4 m 的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了__(23-22)__m.
17.(2014·襄阳)如图,在建筑平台CD 的顶部C 处,测得大树AB 的顶部A 的仰角为
45°,测得大树AB 的底部B 的俯角为30°,已知平台CD 的高度为5 m ,则大树的高度为__(5+53)__m .(结果保留根号)
18.(2014·宜宾)规定:sin (-x)=-sin x ,cos (-x)=cos x ,sin (x +y)=sin x ·cos y +cos x ·sin y. 据此判断下列等式成立的是__②③④__.(写出所有正确的序号)
①cos(-60°)=-12;②sin75°=6+24;③sin2x =2sin x ·cos x ;④sin(x -y )=sin x ·cos y
-cos x ·sin y .
三、解答题(66分) 19.(8分)计算:
(1)sin 230°+cos 245°+3sin60°·tan45°; 解:94
(2)cos 230°+cos 260°tan60°·tan30°+sin 245°.
解:32
20.(8分)在Rt △ABC 中,∠C =90°,a =10,c =20,解这个直角三角形. 解:∠A =30°,∠B =60°,b =103
21.(8分)如果是我国某海域内的一个小岛,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠B =∠D =90°,AB =BC =15千米,CD =32千米.求∠ACD 的余弦值.
解:连接AC ,在Rt △ABC 中,AC =AB 2+BC 2=152千米,在Rt △ACD 中,cos
∠ACD =CD AC =32152=15,∴∠ACD 的余弦值为1
5
22.(10分)如图,在Rt △ABC 中,∠C =90°,BC =8,tan B =1
2,点D 在BC 上,且
BD =AD .求AC 的长和cos ∠ADC 的值.
解:∵在Rt △ABC 中,BC =8,tanB =1
2,∴AC =4.设AD =x ,则BD =x ,CD =8
-x ,由勾股定理,得(8-x )2+42=x 2.解得x =5.∴cos ∠ADC =DC AD =3
5
23.(10分)(2014·常德)如图,A ,B ,C 表示修建在一座山上的三个缆车站的位置,AB ,BC 表示连接缆车站的钢缆.已知A ,B ,C 所处位置的海拔AA 1,BB 1,CC 1分别为160米,400米,1000米,钢缆AB ,BC 分别与水平线AA 2,BB 2所成的夹角为30°,45°,求钢缆AB 和BC 的总长度.(结果精确到1米)
解:根据题意知BD =400-160=240米,CB 2=1000-400=600米,在Rt △ADB 中,sin30°=BD AB ,∴AB =BD sin30°=480米,在Rt △BB 2C 中,sin45°=CB 2BC ,∴BC =
CB 2
sin45°=6002米,AB +BC =(480+6002)米≈1329米
24.(10分)如图,某高速公路建设中需要确定隧道AB 的长度.已知在离地面1500 m 的高度C 处的飞机上,测量人员测得正前方A ,B 两点处的俯角分别为60°和45°.求隧道AB 的长.(3≈1.73)
解:∵OA =1500×tan30°=5003,OB =OC =1500,∴AB =1500-5003≈1500-865=635(m )
25.(12分)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌AB ,放置在教学楼的顶部(如图所示).小明在操场上的点D 处,用1米高的测角仪CD ,从点C 测得宣传牌的底部B 的仰角为37°,然后向教学楼正方向走了4米到达点F 处,又从点E 测得宣传牌的顶部A 的仰角为45°.已知教学楼高BM =17米,且点A ,B ,M 在同一直线上,求宣传牌AB 的高度.(结果精确到0.1米,参考数据:3≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75)
解:过点C 作CN ⊥AM 于点N ,则点C ,E ,N 在同一直线上.设AB =x 米,则AN =x +(17-1)=x +16(米),在Rt △AEN 中,∠AEN =45°,∴EN =AN =x +16,在Rt
△BCN 中,∠BCN =37°,BM =17,∴tan ∠BCN =BN CN =0.75,∴17-1x +20=34,解得x =11
3≈
1.3.经检验:x =11
3是原分式方程的解.答:宣传牌AB 的高度约为1.3米。