DNA密码研究
- 格式:pdf
- 大小:167.40 KB
- 文档页数:8
遗传密码决定蛋白质中氨基酸顺序的核苷酸顺序,由3个连续的核苷酸组成的密码子所构成。
由于脱氧核糖核酸(DNA)双链中一般只有一条单链(称为有义链或编码链)被转录为信使核糖核酸(mRNA),而另一条单链(称为反义链)则不被转录,所以即使对于以双链DNA作为遗传物质的生物来讲,密码也用核糖核酸(RNA)中的核苷酸顺序而不用DNA 中的脱氧核苷酸顺序表示。
遗传密码是一组规则,将DNA或RNA序列以三个核苷酸为一组的密码子转译为蛋白质的氨基酸序列,以用于蛋白质合成。
几乎所有的生物都使用同样的遗传密码,称为标准遗传密码;即使是非细胞结构的病毒,它们也是使用标准遗传密码。
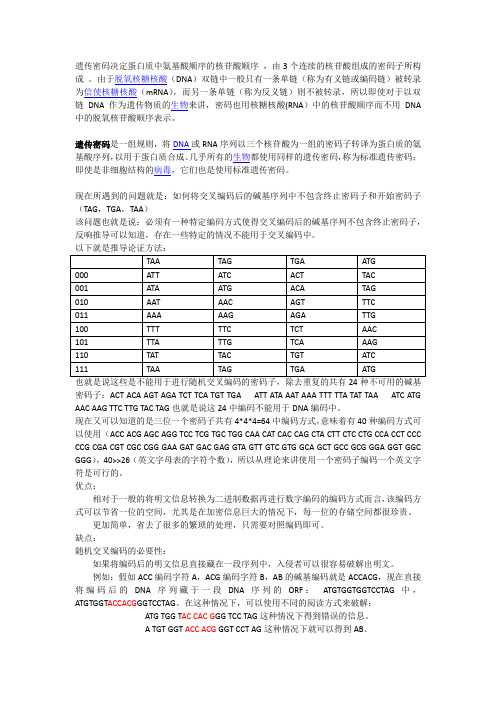
现在所遇到的问题就是:如何将交叉编码后的碱基序列中不包含终止密码子和开始密码子(TAG,TGA,TAA)该问题也就是说:必须有一种特定编码方式使得交叉编码后的碱基序列不包含终止密码子,反响推导可以知道,存在一些特定的情况不能用于交叉编码中。
也就是说这些是不能用于进行随机交叉编码的密码子,除去重复的共有24种不可用的碱基密码子:ACT ACA AGT AGA TCT TCA TGT TGA ATT ATA AAT AAA TTT TTA TAT TAA ATC ATG AAC AAG TTC TTG TAC TAG也就是说这24中编码不能用于DNA编码中。
现在又可以知道的是三位一个密码子共有4*4*4=64中编码方式,意味着有40种编码方式可以使用(ACC ACG AGC AGG TCC TCG TGC TGG CAA CAT CAC CAG CTA CTT CTC CTG CCA CCT CCC CCG CGA CGT CGC CGG GAA GAT GAC GAG GTA GTT GTC GTG GCA GCT GCC GCG GGA GGT GGC GGG),40>>26(英文字母表的字符个数),所以从理论来讲使用一个密码子编码一个英文字符是可行的。

DNA密码的解读DNA是生命的基础,在人类历史中一直是一个神秘的存在。
然而,随着科学技术的飞速发展,我们现在已经可以解读DNA密码,并且开始了对基因组的深度研究。
在这篇文章中,我们将探讨DNA 的结构、功能和解读的意义。
DNA的结构DNA 可以被看做是由四种不同的碱基和一个糖基组成的双螺旋结构。
这四种碱基被简写为 A、T、C 和 G。
糖基和磷酸基片段则被称为核苷酸。
这些碱基通过氢键来结合在一起,并且按照一定的规则被定向排列,形成 DNA 的双螺旋结构。
DNA的功能DNA 的最主要的功能是在细胞的复制和表达中承担重要的作用。
在细胞分裂过程中,每个细胞需要复制其完整的基因组,确保每个孩子都具有完整的基因组。
而在基因表达中,DNA则通过RNA转录来产生各种蛋白质。
这些蛋白质负责各自的生物功能,例如制造酶、激素和结构蛋白等等。
DNA的解读DNA的解读既是一个挑战,也是一个机会。
我们可以通过了解基因组的真实情况来更好地理解人类甚至整个生命的本质。
在基因组研究领域,我们可以探究DNA编码相关的生物学问题,例如遗传疾病、人类进化过程和生物多样性等等。
DNA的解读对于生物医学具有极大的意义。
通过解读基因组,我们现在已经可以检测出许多潜在的遗传疾病,采取更为准确的治疗和预防措施,逐渐减少医疗风险,提高治疗效果。
与此同时,研究发现个体差异导致了药物代谢率的不同,基因组的解读也能帮助医生更好地为患者选择治疗方案和药物。
此外,DNA的解读对于保护生态系统和维护生命多样性也具有重要意义。
通过解读 DNA,我们能够了解不同物种的生态系统互动模式,形成更好的生物多样性保护措施。
同时,DNA测序技术也可以被用来检测野生动物种群,确保他们的健康和繁殖。
结论因此,DNA解读不仅关乎个人健康,也关乎生态系统的健康和维持人类和整个自然世界的平衡和稳定。
DNA解读的研究需要时刻站在人类健康和整个生态系统稳定发展的角度,为人类和自然界的未来奠定一个更可持续的基础。

遗传密码的破译研究在人类历史的长河中,人们一直都致力于探索万物的奥秘。
在现代科学技术高速发展的时代,科学家们的探索之路更加广阔。
人类基因组计划的诞生为人们揭示了人类基因组的秘密,但是遗传密码的破译研究却是人类探索生命奥秘的另一重大突破。
一、遗传密码的基础知识人的基因组来自父母,对于我们来说,父亲和母亲每个人都有26对染色体,其中一对性染色体,即男性为XY,女性为XX。
其中,每个染色体上都有许多基因,而基因是决定我们的外貌、智力以及身体机能的基础单位。
这是我们通常所谓的遗传物质,是由巨大的DNA(脱氧核糖核酸)分子组成。
每个基因都是由DNA中的一条线性片段编码产生的,而且几乎所有的生命都使用类似的DNA编码系统,因此这些编码区被称为通用遗传密码,或者是简称为“遗传密码”。
二、开始解码:从RNA到蛋白质一个基因的特定DNA序列被称为基因型,它只是遗传信息的储存方式。
对于DNA的表现形式,另有一个名为表型的概念。
基因型在实际情况下表现为一个具体的特性,这是由细胞机制通过遗传密码翻译成为蛋白质的。
而翻译的关键是mRNA(信使RNA)分子。
当需要制造特定蛋白质时,基因的DNA信息会转录成一条mRNA,并传到细胞质中的核糖体。
核糖体是一种由蛋白质和RNA分子组成的复合体。
通俗点说,mRNA这条指导蛋白质合成的描述资料在核糖体中被翻译成一条由氨基酸组成的多肽链(即蛋白质)。
氨基酸链的顺序是由基因型中的DNA序列决定的。
三、遗传密码的探索历程破译遗传密码的历史始于1960年代。
当时,计算机刚刚问世,但在计算遗传密码的复杂性上还有一些困难。
Francis Crick和Sydney Brenner利用特殊的分子生物学方法密集地研究了微生物倍数线虫(Nematode)的生命过程,从而发现了三个核苷酸一组所编码的一个氨基酸,建立起遗传密码的框架。
学者们发现,目前为止发现的编码数最少的物种是线虫,只有82个编码。
在降低编码复杂性和提高翻译速度之后,生命系统随着时间的推移变得更加复杂,而核苷酸编码数逐渐增加到了21种。

探索人类基因的遗传密码在探索人类基因的遗传密码的旅程中,我们揭开了生命最深处的秘密。
基因,这些微小的分子,携带着构建和维持我们身体所需的所有信息。
它们是生物体的蓝图,决定了我们的眼睛颜色、身高、甚至我们对某些疾病的易感性。
遗传密码,或者说遗传代码,是由DNA中的四个碱基——腺嘌呤(A)、胸腺嘧啶(T)、胞嘧啶(C)和鸟嘌呤(G)——组成的序列。
这些碱基以特定的顺序排列,形成基因,而基因则编码蛋白质,这些蛋白质执行细胞内的各种功能。
每个基因都是一个由这些碱基组成的长链,它们按照特定的顺序排列,形成了一个独特的遗传密码。
科学家们通过研究这些基因和它们的表达模式,已经能够揭示许多关于人类健康和疾病的信息。
例如,通过比较不同个体的基因序列,研究人员可以识别出与特定疾病相关的遗传变异。
这些发现不仅有助于我们理解疾病的遗传基础,而且还为开发新的治疗方法提供了可能。
然而,遗传密码的探索并不仅仅是关于疾病。
它还涉及到我们对人类进化的理解。
通过比较不同物种的基因组,科学家们可以追踪物种之间的进化关系,了解我们是如何从共同的祖先演化而来的。
这些研究不仅增进了我们对生命多样性的认识,而且还揭示了生命如何在地球上演化和适应。
随着基因编辑技术的发展,如CRISPR-Cas9系统,我们甚至开始有能力直接修改遗传密码。
这为治疗遗传性疾病提供了新的希望,但同时也引发了关于伦理和道德的重要讨论。
我们如何确保这些技术被负责任地使用,以及它们对社会和个体的影响,是我们必须面对的挑战。
总之,探索人类基因的遗传密码是一个不断进步的领域,它不仅推动了我们对生命科学的理解,还对我们的生活方式和未来产生了深远的影响。
随着技术的不断进步,我们可以期待在未来揭开更多关于我们自身的秘密,同时也必须谨慎地考虑这些发现带来的后果。

DNA解密遗传密码中的生命密码DNA(脱氧核糖核酸)是生物体中重要的遗传物质,它承载着生物体的遗传信息。
随着科学技术的进步,人们逐渐揭开了DNA中蕴含的秘密,解密了遗传密码,探索了生命密码。
1. DNA的结构与作用DNA是由两条互补的链构成的双螺旋结构。
每条链由糖和磷酸分子交替组成,而糖的每个分子上连接着一个碱基,包括腺嘌呤(A)、胸腺嘧啶(T)、鸟嘌呤(G)和胞嘧啶(C)四种。
这些碱基的配对规则是A与T相互配对,G与C相互配对。
这种碱基配对决定了DNA 的复制方式。
2. DNA的复制DNA的复制是生物遗传的基础过程之一。
在细胞分裂时,DNA会通过一系列的步骤进行复制。
首先,DNA双链被酶酶解,形成两个互补的单链。
然后,在每条单链上合成新的互补链,形成两个完全相同的DNA分子。
这个过程保证了遗传信息的传递和稳定。
3. 遗传密码的解读DNA中的遗传信息以三个碱基的序列编码的方式存在,称为密码子。
每个密码子对应一个氨基酸,而氨基酸是蛋白质的组成单位。
生物体通过DNA的转录和翻译过程将遗传信息转化为蛋白质。
3.1 DNA的转录转录是指DNA信息转移到RNA分子上的过程。
RNA的结构与DNA类似,但糖的成分是核糖,而不是脱氧核糖。
转录过程中,酶将一条DNA链作为模板,合成与DNA链互补的mRNA分子。
因此,DNA中的A会与mRNA中的U配对。
3.2 RNA的翻译翻译是指mRNA上的遗传信息转化为蛋白质的过程。
遗传信息以三个碱基为一个单位,称为密码子。
对应的氨基酸由特定的tRNA分子携带,并通过蛋白质合成机器将氨基酸连接起来,形成蛋白质链。
4. 基因突变与遗传疾病DNA中的碱基序列决定了遗传信息,但在复制、转录和翻译过程中,有时会发生突变,即碱基序列的改变。
突变可能会导致蛋白质的结构或功能发生异常,从而导致遗传疾病的发生。
例如,突变可能导致酶的活性降低,导致代谢错误和遗传性疾病的发展。
5. DNA解密的应用DNA解密在生物学和医学上有着广泛的应用。

遗传密码的发现和研究进展遗传密码是指DNA分子中编码氨基酸序列信息的规则。
通过遗传密码,人们得以解读每个DNA分子中的基因序列,并确定氨基酸序列的形成。
在人类历史上,发现遗传密码是开启生物学新篇章的重要一步。
下面我们来详细了解遗传密码的发现和研究进展。
一、遗传密码的发现遗传密码的发现是在20世纪50年代初完成的。
当时,孟德尔遗传学的原理已经集成了大量遗传信息,但是科学家们需要更多的数据才能进一步探究这一理论。
于是,从20世纪50年代末开始,分子生物学研究者逐步揭示了DNA的组成和作用,包括碱基对规则、DNA夹带信息到蛋白质的过程等。
1953年,Watson和Crick首次叙述了DNA的双螺旋结构,这项成果成为了遗传密码研究的基石。
几年后,研究者使用DNA和RNA来合成短链肽,从而推断出在蛋白质合成中等位于核苷酸和氨基酸之间的信号分子——纽cleic酸酶。
之后,研究者开始探索DNA和RNA的具体组成,并找到了具体影响DNA和RNA特质的位置。
在研究中,研究者采用了各种方法来产生不同的三个半乳糖和氨基酸基序列,使用不同的同位素标记物来测量所组成的肽链中的氮15基团的位置。
通过比较这些氮5位置的加入,研究者得出了24个不同的三联密码子——遗传代码的基本元素——并将它们与氨基酸级别相关联。
遗传密码的发现为研究生物化学以及遗传学打开了一扇通向新思维的大门。
二、遗传密码的研究进展舌咽神经节的神经元成为了最受欢迎的遗传密码研究对象。
这些神经元排列在一起,形成码字,这些码字可以表示具有功能、性质和形态特征的蛋白质。
研究者发现,在标准遗传密码中的一个密码子变成了另一个仅有一个核苷酸序列的密码子时,这些神经元仍然能够遵守相同的原则——在蛋白质链的同一位置上具有相同的氨基酸。
研究者还发现,在遗传密码内部,同一个氨基酸可以由不同的三联密码子兑现,这被称为遗传密码上的“冗余”。
这种冗余性是生命演化中的结果,它使得产生密码的编码错误率降低了数量级。
DNA编码基因密码的秘密DNA作为生物体中传递遗传信息的核苷酸序列,一直以来都被视为生命的密码。
然而,DNA中最为神秘的一部分是其编码基因密码的机制。
基因密码的解密不仅揭示了生命的本质,还有助于人类理解遗传疾病的发生机制。
本文将探讨DNA编码基因密码的秘密以及相关的重要研究进展。
首先,我们需要了解基因密码是如何工作的。
在DNA分子中,四种不同的碱基(腺嘌呤、鸟嘌呤、胸腺嘧啶和鳗虫胺嘧啶)按照一定的顺序排列,形成了三个碱基的组合,称为密码子。
每个密码子对应着一个特定的氨基酸,而氨基酸则是构建蛋白质的基本单位。
因此,DNA的碱基序列可以看作是特定蛋白质的编码。
DNA编码基因密码的秘密首次被揭示是在上世纪60年代,由美国科学家Marshall Nirenberg和他的团队完成了一系列重要实验。
他们使用人工合成的RNA链和细胞质中的细胞器来揭示不同的细胞密码子与氨基酸之间的对应关系。
这项研究为后续的基因密码研究奠定了基础。
进入21世纪以来,随着高通量测序技术的发展,科学家们能够更加深入地研究基因密码的机制。
最新的研究表明,基因密码的解读并不像我们过去认为的那样简单。
除了主要的Nirenberg编码,还存在一些例外的密码子对氨基酸的编码方式。
这些例外密码子对氨基酸的特定编码可能与生物体的个体差异和疾病的发生密切相关。
了解基因密码的机制对人类的健康具有重要的意义。
许多遗传疾病都与基因密码中的突变相关。
例如,囊性纤维化是一种严重的遗传疾病,患者的CFTR基因存在一个密码子突变,导致蛋白质无法正确折叠和定位,从而引发严重的器官损伤。
对基因密码的深入研究可以帮助我们更好地理解遗传疾病的发生机制,进而寻找治疗和预防的方法。
近年来,科学家们还发现基因密码在其他领域的重要应用。
例如,在合成生物学中,利用基因密码的原理可以定向设计和合成特定的蛋白质,进而用于生物医学和工业应用。
此外,基因密码的研究还为破译古代DNA提供了重要线索,帮助我们了解古代生物和人类进化的过程。
基于DNA计算的密码学技术研究DNA技术是人类历史上的一项伟大发明,它不仅可以在生物学领域中发挥着重要的作用,也在计算机科学领域中展现出惊人的应用价值。
基于DNA计算的密码学技术作为新兴的密码学分支,在安全领域中具有广阔的应用前景。
一、DNA计算的基本原理DNA计算作为一种新兴的计算模型,其基本原理是通过编码DNA序列中的信息,将问题转化为某些特定的DNA序列在反应中的扩增情况,最终输出得到解码后的数据。
由于DNA计算拥有极高的并行性和复杂度,因此可以更准确和高效地解决某些特定的计算问题。
而在密码学技术中,DNA计算不仅能够对传统的密码算法进行优化,还可以进行很多其他领域用途的开发。
二、基于DNA计算的密码学技术1. DNA加密算法对于传统的加密算法而言,破解方法一般是通过暴力破解或者密码学攻击。
而基于DNA加密算法的密码学技术可以更有效地避免这些攻击方式。
具体来说,DNA序列作为独立的密钥进行加密和解密,其安全性远远高于传统的加密算法,同时也难以被破解,这使得DNA加密算法在某些特定领域中得到了广泛应用,例如商业保密、军事保密等领域。
2. DNA隐写术DNA隐写术是指将信息隐藏在DNA序列中,使得外部的人无法发现。
这种密码学技术的应用范围很广,同时也是目前比较热门的一个研究领域。
DNA隐写术不仅可以用于保密和信息传递等方面,还可以用于防伪和授权验证等应用领域。
由于DNA隐写术的安全性极高,因此被广泛应用于金融、法律、医疗等领域。
3. DNA签名技术由于DNA序列具有高度的唯一性和可靠性,因此它可以作为一种有效的签名技术。
DNA签名技术可以帮助人们更好地实现数字签名技术,从而在数字安全领域中起到重要的作用。
同时,DNA签名技术还可以应用到电子票据、契约、证书等领域,从而保证数字签名的安全性和可靠性。
三、基于DNA计算的密码学技术的优势1. 安全性高由于DNA序列作为独立的密钥进行加密和解密,因此其安全性远远高于传统的加密算法。
遗传学中的DNA遗传密码探究DNA遗传密码是我们日常生活中经常听到的一个词汇,它似乎与我们的基因组密不可分。
事实上,DNA遗传密码影响着我们的生长、发育、代谢等方方面面。
本文将探讨遗传学中的DNA遗传密码。
DNA遗传密码概述首先,我们需要了解什么是DNA。
DNA全称为脱氧核糖核酸,是生命活动中最重要的分子之一。
它是一种复杂的聚合物,由四种不同的碱基序列构成:腺嘌呤(A)、胸腺嘧啶(T)、鸟嘌呤(G)和胞嘧啶(C)。
这些碱基在DNA分子中以特定的方式排列,并通过化学键结合在一起,形成一个长链。
DNA遗传密码是由这些碱基序列编码的。
具体来说,一段DNA序列中每三个碱基被称为一个密码子,每个密码子可以翻译成一种氨基酸。
氨基酸是生命活动中构成蛋白质的基本单位。
因此,DNA遗传密码控制着蛋白质的合成过程。
这一过程被称为转录。
转录的过程是通过RNA分子媒介实现的。
RNA分子是由核苷酸组成的聚合物,它们与DNA序列相似,但是缺少胸腺嘧啶,而代之以尿嘧啶(U)。
RNA分子通过与DNA序列互补配对,将DNA序列转录成RNA序列。
RNA序列与DNA序列相比,具有较弱的稳定性。
因此,在转录完成后,RNA分子往往会经过剪接和修饰等过程,形成最终的RNA分子。
这一分子被称为信使RNA(mRNA),它负责将DNA序列中编码的信息传递给蛋白质合成的过程。
这一过程被称为翻译。
翻译的过程是通过核糖体等酶媒介实现的。
在这一过程中,mRNA分子被读取,并翻译成氨基酸序列。
氨基酸序列进一步通过化学键结合在一起,形成一个长链。
这一链经过折叠和修改等过程,最终形成蛋白质。
DNA遗传密码的破译DNA遗传密码的破译是现代生命科学的一个里程碑。
在20世纪50年代,G.Crich和J.D.Watson通过对DNA分子结构的研究,提出了DNA分子具有双螺旋结构的假设。
1961年,美国生物学家M.Nirenberg等人证实了这一假设。
他们利用一种称为光学方法的技术,将RNA分子注入细胞中,观察细胞中是否产生新的蛋白质。
DNA序列与遗传密码解析DNA(脱氧核糖核酸)是生物体内负责遗传信息传递的核酸分子。
它由含有四种碱基(腺嘌呤,胸腺嘧啶,鸟嘌呤和胞嘧啶)的线性链条组成。
DNA序列和遗传密码是生命起源和进化中的核心要素。
本文将探讨DNA序列与遗传密码的意义及其解析方法。
DNA序列是DNA分子中碱基的排列顺序。
这个序列是组成生物体的基本单位,决定了生命体的特征和功能。
通过分析和解读DNA序列,我们能够了解生物体的遗传信息和进化历程。
解析DNA序列是生物学和遗传学研究的重要手段,也是基因工程和生物技术的基础之一。
遗传密码是一种特殊的编码方式,用来将DNA序列中的碱基信息转化为核糖体在蛋白质合成过程中所识别的氨基酸。
遗传密码由三个碱基组成的密码子来表示,每个密码子对应一个氨基酸或终止信号。
在蛋白质合成过程中,mRNA(信使RNA)通过核糖体与tRNA(转运RNA)相互作用,将特定的氨基酸带入蛋白质合成链中,从而合成出特定的蛋白质。
DNA序列的解析主要包括基因识别、密码子译码和蛋白质合成三个方面。
基因识别是指通过比对DNA序列与已知的基因库来寻找和识别潜在基因。
这项工作可以利用计算机算法进行,通过分析DNA序列中的起始和终止密码子以及编码区域来确定基因的位置和可能功能。
密码子译码是将DNA序列中的密码子与相应的氨基酸进行对应,得到相应的蛋白质合成信息。
在密码子表中,有61个密码子对应不同的氨基酸,还有3个密码子用于指示终止蛋白质合成的结束。
研究人员通过构建密码子表和运用分子遗传学和生物化学技术,成功揭示了遗传密码的结构和功能。
蛋白质合成是基于DNA中的密码子进行的,它是将DNA信息转化为蛋白质的过程。
在蛋白质合成过程中,mRNA通过核糖体与tRNA相互作用,在多个步骤中将氨基酸连接成一个多肽链。
通过分析DNA、mRNA和tRNA之间的相互作用以及氨基酸的连接规则,我们可以更好地理解蛋白质的合成过程。
DNA序列和遗传密码的解析在生物科学研究中发挥着重要的作用。
Distribution of Codon Locations in DNA SequenceWu XiaoxiaCollege of Mathematics and Statistics, Wuhan University, Wuhan, 430072, Hubei, ChinaE-mail: wuxiaoxia_1015@ AbstractIn the analysis of DNA sequence, this paper introduces a method: stationary m-order Markov chain to study codon locations, from which the estimators of parameters can be obtained via its MLE. This paper gives a description of the exact distribution of the distance between codon occurrences along a DNA sequence and an asymptotic distribution of codon count through the Gaussian distribution. Keywords: codon; stationary m-order Markov chain; transition matrix. CLC number : O 2121 Introduction of the model in DNA sequenceA biological sequence is either a DNA sequence or a protein sequence, which is a finite sequence of letters either in the 4-letter DNA alphabet {},,,Αa c g t =. To model a biological sequence, we will consider models for random sequences of letters ()i i X X ∈= on a finite alphabet A , where is the set of integers.We consider a good model, the model Mm as an ergodic stationary m-order Markov chain on a finite alphabet A with transition matrix()()()()121121,,,,,m m m m a a a a a a a a Απ++∈Π=such that()()121111,|,,m m i m i m i m a a a a P X a X a X a π++−−====Define ()()12112,m i m i m a a a P X X a a a i µ+−==∀∈ , where µas a stationary distribution satisfy the equation µµ=Π, such that the equation()()()12121121,m m m m b a a a ba a a ba a a a Αµµπ−−∈=∑is satisfied for all 12()mma a a ∈ A .( see Ref.[1])A coding DNA sequence is naturally read as successive non-overlapping 3-letter words called codons. The codons are then translated into amino acids via the genetic code to produce a protein sequence .It is known that there are 64 codons for they are the compositions of three different letters from Α.The codons are used to be translated into amino acids except 3 terminators. And we know there are only20 amino acids. So there are several different codons coding for the same amino acid, and often the first two letters of some codon suffice to determine the corresponding amino acid. Therefore, letters may have different importance depending on their positions with respect to the codon partition. To distinguish the letter probabilities according to their positions modulo of 3 in the coding DNA sequence, we consider a stationary Markov chain with three distinct transition matrices 12,∏Πand3Π, such that for()121,m m a a a a Α+∈ and {}1,2,3k ∈,()()121313131,|,,,k m m j k m j k m j k m a a a a P X a X a X a j π++++−+−====∀∈This is model 3Mm . The index {}1,2,3k ∈is called phase and represents the position of aletter inside a codon. The stationary distribution k µon mΑ is given by()1231312(),k m j k m j k m a a a P X X a a a j µ+−++==∀∈such that the equations()(){}121121121(),,1,2,3k m k m k m m b a a a ba a a ba a a a k µµπ−−−∈Α=∈∑are satisfied for all 12()m m a a a Α∈ .Robin and Daudin [2] obtained the recursive formula for the exact distribution of the distance D between two word occurrences. It was first proposed for independent and uniformly distributed letters by Blom and Thorbum [3] . Similar results are derived in Robin and Daudin [4] and Stefanov [5] for the probability distribution of the distance between any word in a given set. The method of obtaining the exact distribution of the word count presented here generalizes the result that Gentleman and Mullin [6] obtained for case that the sequence is composed of i.i.d. letters, where each letter occurs with equal probability. The martingale and the conditional ones have advantage to provide explicit formulas for the asymptotic variance for the first order markov chain model. They are both due to Prum et al. [7] and to Schbath [8] for higher order models and Phased model. In this article, we consider the location of codon and apply the methods above to obtain its distribution.2 Estimation of the model parametersIn this paper we assume that 12nX X X is a stationary 1-order Markov chain on Αwithtransition matrix ()(),,a b a b π∈ΑΠ=and stationary distribution ()()a a µ∈Αfor simplicity.Generally, a DNA sequence contains a promoter before it starts to read the codons with hereditable information and ends with a terminator in the process of gene transcription. But in some other particular cases, it has not promoter, so the reading frame is not fixed and the results of transcription are distinct. Here we just consider the general case. That is it has a promoter and the reading frames are all fixed. So the sequence 12nX X X starts from the first codon and ends with aterminator. Here we assume that n can be divided by 3, otherwise we take []/33n n ′=×.Modeling a biological sequence, we need choose a probabilistic model and estimate the parameters according to the unique realization that is the biological sequence. We now give an estimator that maximizes the likelihood of 1M model. Assume 12nXX Xis a stationary Markovchain on A with transition matrix ()(),,a b a b π∈ΑΠ=and stationary distribution ()()a a µ∈Α. Thelikelihood L of the model is(){}()()()()()31,1,,,,1,2,3,k N ab k k a b k L a b a b k X a b πµπ∈Α=∈Α∈=∏∏where ()k N ab denotes the number of the 2-letter word ab which ends at301,1,2,33n i k i k +≤≤−=⎛⎞⎜⎟⎝⎠in the random sequence 12nX X X .To find the transition probabilities that maximize the likelihood, one maximizes the log likelihood(){}()()()()31,1log ,,,,1,2,3log log ,k kka b k L a b a b k X N ab a b ΑπΑµπ∈=∈∈=+∑∑We can separately maximize()()31log ,kkk b N ab a b π=∈Α∑∑for a Α∈, keeping in mind that(){},1,1,2,3kb a b k π∈Α=∀∈∑. Leta ∈Αand choose c Α∈, we have()()()()()()333111log ,log ,log 1,kkkkkkk b k b ck b cN ab a b N ab a b N ac a b Απππ=∈=≠=≠⎛⎞=+−⎜⎟⎝⎠∑∑∑∑∑∑ And for b c ≠,()()()()()()()31log ,,,,k k k k k b k k k N ab a b N ab N ac a b a b a c Αππππ=∈∂=−∂∑∑{},1,2,3k ∈.All the partial derivatives equal to zero means that ()()()(),,,k k k k N ab N ac b a b a c Αππ=∀∈. This implies inparticular that()()()()(),.,,kk d kd kkd N ad N ab N ad b a b a d Αππ∈Α∈Α∈Α==∀∈∑∑∑ It follows that ()()()()(){}1ˆ,,1,2,3.k k k kk d N ab N ab a b k N ad N a π−∈Α==∀∈⋅∑For notational convenience, theestimators mainly used in the reminder of the article will be ()()()1ˆ,k k k N ab a b N a π−= since ()()N a N a ⋅=except for the letter of the sequence for which the counts differ by 1.3 Exact distribution of the distance between codon occurrencesHere we are concerned with the length of the gaps between codon occurrences. Now wedescribe how to obtain the exact distribution of the distance between successive occurrences of a codon.Let 123ωωωω=be a word of length 3 on a finite alphabet A , where ωis a codon. We assume that12nX X X is a stationary 1-order Markov chain on A with transitionmatrix ()(),,k k a b a b Απ∈Π=and stationary distribution ()()a a Αµ∈. Here we are interested in the statistical distribution of the distance D between two successive occurrences of ωand more precisely in the probability()()3( occurs at 3i + 3d and there is no occurrence of at 3i + 3k, 0<k<d| occurs at 3i),D f d P D d P ωωω===where d > 0,ωoccurs at 3i means it ends at 3i . If ,3n di >− then ()0D f d =. If 13n d i≤≤−,then the event {}E= occurs at 3i + 3d ω can be decomposed into several disjoint events.{}{}()122E = occurs at 3i + 3d and there is no occurrence of at 3i + 3k, 0<k<d E = occurs at 3i + 3d and there are some occurrence of at 3i + 3k, 0<k<d E h =there is no occurrence of at 3i +3k, 0<k<h<d an ωωωωω{}d occurs at 3i + 3d and 3i+3h ωWe can get()()1| occurs at 3i .D f d PE ω=Moreover,2E can be decomposedas ()1221.d h E E h −==∪So that ()112121d h E E E E E h −===∪∪, therefore,()()()()()()()()()()()()()()()()()112133213313132131111111332332131131111| occurs at 3i | occurs at 3i | occurs at 3i ,,,,,D d h d h d d D h d d d h D h f d P E P E P E h f h f h ωωωµωµωπωωπωωµωµωµωπωωπωωµω−=−−−−=−−−−===−=−⎡⎤=−⎢⎥⎣⎦∑∑∑where 13n di≤≤−, elsewise ()0D f d =.4 Codon count distributionWe know that a codon 123ωωωω=be a word of length 3 on a finite alphabet A and ()i i X X ∈= is a random sequence on Α.This section is devoted to consider the statisticaldistribution of the count ()3N ωof the codon ωin the sequence 12n X X X . In the followingsubsection we will give an asymptotic distribution: the Gaussian regime.We assume that ()i i X X ∈= is a stationary first-order Markov chain on Α with transition probabilities (),k k a b π∈Ζand stationary distribution ()a a µ∈Α.()/331n i i N Y ω==∑, where(){}ends at position 3i in X i i Y Y I ωω==,13n i ≤≤. So we have the expectation and variance of()3N ωbelow()(){}()/3331ends at position 3i in X 3n i nE N P ωωµω===∑ ()()()()()()()()()22222333339n Var N E N E N E N ωωωωµω⎡⎤=−=−⎣⎦ ()()(){}()()()()()()()()()()2/3/3/322311133133233131212323133233212323132 ends at position 3i and 3j 32,,,32,,,33n n n i i i j n i i i j ni j j i ni j i E N E Y E Y YY nP nn n i ωµωωµωµωπωωπωωπωωµωµωπωωπωωπω==≤≠≤≤<≤−−≤<≤−⎛⎞⎛⎞⎜⎟==+⎜⎟⎜⎟⎝⎠⎜⎟⎝⎠=+=+⎛⎞=+−⋅⎜⎟⎝⎠∑∑∑∑∑()1311n i ω−=∑So we can get()()()()()()()()()()()()()231123322333212323131311232231313112,,,3392,339ni i n i i n n n Var N i n n n i ωµωµωπωωπωωπωωµωµωµωπωωµωµω−−=−−=⎛⎞⎜⎟⎝⎠⎛⎞=⎜⎟⎝⎠=+−⋅−+−⋅−∑∑ˆN N ωω− and theasymptotic variance.From section 3, we can get the maximum likelihood estimator ()3ˆN ωof ()()3E N ω: ()()()()212323322ˆN N N N ωωωωωω=Indeed, ()3N ωis a natural estimator of ()()212323,N ωωπωω, and ()()()3212323,N N ωωωπωω−is approximately a martingale as it is shown below.We introduce the martingale ()()/311|n n i i i i M Y E Y −==−∑F with ()132i i X X σ+= F . It is easyto verify that ()311|nnn EMM−=F . Moreover, we have()()(){}{}(){}()1112311223112323| ends at position 3i | ends at position 3i-1 and occurs at 3i | ends at position 3i-1 ends at 3i | ends at position 3i-1,i i i i i E Y P P E I I I ωωωωωωωωωωπωω−−−−====F F F F(){}()()()/3/311232311212323| ends at position 3i-1,,n n ii i i E Y I N ωωπωωωωπωω−====∑∑FTherefore,()()())3212323,M N N ωωωπωω=−.The next step we will establish theasymptotic normality of n M of martingales.Theorem 1: Let (),1,,n i i n ξ= be a triangular array of d-dimensional random vectors such that2,2n iE ξ<∞ , and Vbe a positive d d × matrix.Put (),,1,,,n i n n i σξξ= F ,(),,1|n i n i E ξ−F denotes the conditional expectation vector of ,n i ξand(),,1|n i n i Cov ξ−F denotes the conditional covariance matrix of ,n i ξ. If as n →∞,()(),,11|0nPn in i i i E ξ−=⎯⎯→∑F ,()(),,11|nn in i i ii Cov V ξ−=→∑F ,()(),,110,0nPn in i i iii P εξε−=∀>>⎯⎯→∑F ,Then()1,0,ni n iDN V ξ=⎯⎯→∑. ( see Ref. [9])Theorem 2: Let()()()[]212323323,1,V µωωπωωπωω=−, we have(0,)DMN V⎯⎯→as n→∞.Proof: This is an application of T heorem 1 for one-dimensional random variables()(),1|n i i i iY E Yξ−=−F()iholds for(),1|0n i iEξ−=F. We have to check that()/3,11|nn i iiVar Vξ−=→∑F as n→∞. Since i Y is a 0-1 random variable, we have()()(){}()()[]1112323323221||ends at position 3i-1,1,|i ii i i iY YIVar E E Yωωπωωπωω−−−−=−⎡⎤⎣⎦=F F FWe thus obtain()()()(){}()()[]()()()[]()()()[]/3,11/311/311/3123233231212323323212323323|||ends at position 3i-1,1,,1,,1,111,n1nn i iini i iini iiniVar VarVar Y E YVar YINnnnV asnξωωπωωπωωωωπωωπωωµωωπωωπωω−=−=−==−−−−=→∞=====→∑∑∑∑FFFThe third equation comes from ()()1|i i iE E Y EY−=F and the convergence follows from thelarge numbers:()()212212/N nωωµωω→. Finally,,2n iξ≤, so that ()2,0,4/,0n in Pεεξε∀>∀>>=, establishing condition()iii.()()())3212323,(0,)DN N N Vωωωπωω−⎯⎯→,as n→∞.Theorem 3: As n→∞()()()()()()221232333220,DN NN NNωωωωωσωω−⎞⎯⎯→⎟⎠, where()()()()()()[]()()[]2332232322212222µωσωµωµωωµωµωωµω=−−,()()()()()()321232*********,,,µωµωωπωωµωπωωπωω==,()()()32322323,µωωµωπωω=.Proof: Consider()()())3212323ˆ,nT N Nωωωπωω=−, where()()()32332322ˆ,NNωωπωωω=. We have()()()()()()()()()321232321232332332322323ˆ,,,,nnT N NNN NNωωωπωωωωπωωπωωωωωωωπωω=−−⎤⎡⎤⎦⎣⎦=−⎤⎦′=WherenM′ is the martingale()()()/3232311nn i i iiM Y E Yωωωω−=⎡⎤′=−⎣⎦∑F. We know()110,DMN V⎯⎯→ from Theorem 2, where()()()11212323323,1,V Vµωωπωωπωω⎡⎤==−⎣⎦.Similarly,()220,DnM N V′⎯⎯→, where()()()()()22/32312232332311lim,1,ni iniV Var Ynωωµωπωωπωω−→∞=⎡⎤=⎣⎦−=∑F()()[]()()()()()()(){}()()()()()(){}()()()()()(){}/3/312323111/31232311123231131111n ni j j ji jni i i i i iii i i j j jni jCov M EM M EMn n n nE M Mn nnE Y E Y Y E Yi inE Y E Y Y E YnE Y E Y Y E Ynωωωωωωωωωωωωωωωωωω−−==−−=−−≤≠≤′′′−−′=⎡⎤⎡⎤=−−∑∑⎣⎦⎣⎦⎡⎤⎡⎤=−−+∑⎣⎦⎣⎦⎡⎤⎡⎤−−⎣⎦⎣⎦∑F FF FF F()()()()()(){}/312323111ni i i i i iiE Y E Y Y E Ynωωωωωω−−=⎡⎤⎡⎤=−−∑⎣⎦⎣⎦F FThe last equation comes from()()()()()()()()()()()()()()()() ()()()()12323123231231232323220,i i i j j ji j i j j j i i i ji j i jE Y E Y Y E YE Y Y E Y E Y E Y E Y E Y YE Y Y EY E Yi jωωωωωωωωωωωωωωωωωωωωωωωω−−−−−−=−−+=−=∀≠⎡⎤⎡⎤⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎣⎦⎣⎦F FF FAnd because of()()()23i i i iY Y Y Yωωωω=≡, we have()()()()()(){}()(){}()()()/31232311/3221112/311/3111112211211as n.ni i i i i iini i i i i iini i iini i iiCov E Y E Y Y E YE Y Y E Y E YnE Y E YnVar Y E YnV V V Vωωωωωω−−=−−=−=−=′⎡⎤⎡⎤−−⎣⎦⎣⎦⎡⎤=−−⎣⎦⎡⎤=−⎣⎦=−→===→∞∑∑∑F FF FFFSo we have11122122;n DnV VMNV VM⎛⎞⎛⎞⎞⎛⎞⎯⎯→⎜⎟⎜⎟⎟⎜⎟⎜⎟⎝⎠⎠⎝⎠⎝⎠′.Note that the Law of Large Numbers guarantees that almost surely()()()()2122221222NNωωωµωωµω→as n→∞.From above we can deduce thatnT converges in distribution to ()()230,Nσωwith()()()()()()()()()()()()212212323323222lim31limlim,2222221221221122122222,1,1Var T nnNMnM Mn nn NV V Vσωωωωµωωµωωµωµωµωωµωωπωωπωωµω=→∞=→∞′=→∞=+−−⎛⎞⎫⎪⎬⎪⎪⎩⎭⎛⎞⎜⎟⎝⎠⎛⎡⎤⎜⎣⎦⎝=−()()()()()()()()()()()()()()()()()()21222212323323223222123232232221222323222,1,1,µωωµωµωωπωωπωωµωµωµωµωωπωωµωµωµωµωωµωµωωµω−−⎞⎟⎜⎟⎠⎡⎤⎡⎤⎣⎦⎣⎦⎡⎤⎡⎤⎣⎦⎣⎦⎡⎤⎡⎤⎣⎦⎣⎦=−=−=−−Therefore, we have proved()()()()()()221232333220,DN NN NNωωωωωσωω−⎞⎯⎯→⎟⎠. So the proof of theorem 3 is finished.References[1] Senoussi,R.(1990) Statistique asymptotique Presque-sure de modeles statitiques conves, Ann.Inst.Henri Poincare(26):19-44.[2] Robin S, Daudin JJ (1999). Exact Distribution of word occurrences in a random sequence of letters,J. Appl. Prob(36):179-193.[3] Blom,G. and Thorburn,D.(1982). How many random digits are required until given sequences are obtained?, J.Appl. Probab(19):518-531.[4] Robin S, Daudin J.J (2001). Exact distribution of the distances between any ccurrences of a set of words. Ann. Inst. Statist. Math, 53,(4): 895-905.[5] Stefanov,V.(2003). The intersite distances between pattern occurrences in strings generated by general discrete and continuous time models: an algorithmic approach, J.Appl. Probab.: 40.[6] Gentleman, J. and Mullin, R. (1989). The distribution of the frequency of occurrence of nucleotide subsequences, based on their overlap capability, Biometrics (45): 35-52.[7] Prum,B.,Rodolphe,F., and Turckheim, et.(1995). Finding words with unexpected frequencies in dexoxyribonucleic acid sequences, J.Roy. Statist. Soc. Ser. B, (57):205-220.[8] Schbath, S. ( 1995). Compound Poisson approximation of word counts in DNA sequences, ESAIM Probab. Statist.,(1):1-16.[9] Dacunha-Castelle, D. and Dufflo, M. (1983). Probabilites at statistiques 2. Problems a temps mobile, Masson.。