7.5 用力法计算超静定结构在支座移动和温度变化时的内力

用力法求解超静定结构概述超静定结构是指结构中的支座和约束条件多于结构自由度的情况。

用力法是一种经典的结构分析方法，常用于求解超静定结构。

本文将介绍用力法求解超静定结构的基本原理和步骤，并通过实例加以说明。

一、基本原理用力法的基本原理是根据平衡条件和变形约束，通过假设未知力的大小和方向，建立力的平衡方程和变形方程，解出未知力和结构的变形。

用力法适用于各种类型的结构，包括梁、柱、桁架等。

二、步骤用力法求解超静定结构的步骤如下：1. 选择合适的剖面根据结构的几何形状和约束条件，选择合适的剖面，将结构分割为若干个部分。

2. 假设未知力的方向和大小根据结构的特点和约束条件，假设未知力的方向和大小。

通常，未知力的方向可以根据结构的几何形状和外力的作用方向来确定，而未知力的大小则需要通过力的平衡方程来求解。

3. 建立力的平衡方程根据假设的未知力和结构的几何形状，建立力的平衡方程。

平衡方程包括力的平衡条件和力的矩平衡条件。

4. 建立变形方程根据结构的变形情况和约束条件，建立变形方程。

变形方程可以根据结构的刚度和约束条件来确定。

5. 解方程将力的平衡方程和变形方程联立，解方程组得到未知力和结构的变形。

6. 检验结果将求解得到的未知力和结构的变形代入原平衡方程和变形方程中，检验结果的准确性。

如果结果符合平衡和变形的要求，则求解成功；如果结果不符合要求，则需要重新假设未知力并重新求解。

三、实例分析为了更好地理解用力法求解超静定结构的步骤和原理，下面以一个简单的梁结构为例进行分析。

假设有一根悬臂梁，在梁的自重和外力作用下，需要求解支座反力和梁的变形。

1. 选择合适的剖面选择悬臂梁的剖面，将梁分割为两个部分：悬臂部分和支座部分。

2. 假设未知力的方向和大小假设支座反力的方向向上，大小为R。

3. 建立力的平衡方程根据力的平衡条件，可以得到悬臂部分的平衡方程：R - F = 0，其中F为梁的自重。

4. 建立变形方程根据梁的几何形状和约束条件，可以建立悬臂部分的变形方程，得到悬臂部分的弯矩和挠度。

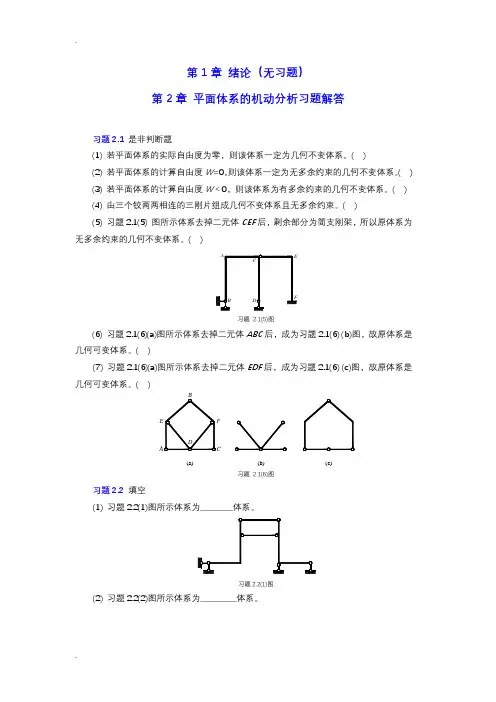
年国家开放大学电大自己《土木工程力学》形成性考核及答案2022年土木工程力学（本）形成性考核册土木工程力学（本）形成性考核册作业一一、选择题（每小题2分，共20分）1．三刚片组成几何不变体系的规则是（B）A三链杆相联，不平行也不相交于一点B三铰两两相联，三铰不在一直线上C三铰三链杆相联，杆不通过铰D一铰一链杆相联，杆不过铰2．在无多余约束的几何不变体系上增加二元体后构成（C）A可变体系B瞬变体系C无多余约束的几何不变体系有多余约束的几何不变体系3．瞬变体系在一般荷载作用下，（C）A产生很小的内力B不产生内力C产生很大的内力D不存在静力解答4．已知某体系的计算自由度W=-3，则体系的（D）A自由度为3B自由度等于0C多余约束数等于3D多余约束数大于等于35．不能作为建筑结构使用的是（D）A无多余约束的几何不变体系B有多余约束的几何不变体系C几何不变体系D几何可变体系6．图示桁架有几根零杆（D）A2C4D6FP7．下图所示结构的弯矩图形状应为（A）FPABCD图1FP8．图示多跨静定梁的基本部分是（B ）AAB部分BBC部分CCD部分DDE部分ABCDE9．荷载作用下产生桁架位移的主要原因是（AA轴向变形B弯曲变形C剪切变形D扭转变形10．三铰拱在集中力作用下其合理拱轴线形状是（D）A折线B圆弧C双曲线D抛物线二、判断题（每小题2分，共20分）1．多余约束是体系中不需要的约束。

（）2．如果体系的计算自由度大于零，那么体系一定是几何可变体系。

（）3．两根链杆的约束作用相当于一个单铰。

（）4．一个体系是有n个自由度的几何可变体系，那么加入n个约束后就成为无多余约束的几何不变体系。

（）5．两刚片用三链杆相联，且三链杆平行不等长，则构成瞬变体系。

（）6．图示两个单跨梁，同跨度同荷载。

但横截面形状不同，故其内力也不相同。

（√）FPFP7．三铰拱的矢高f越大，水平推力也越大。

（）8．求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。

力法、位移法求解超静定结构讲解
超静定结构是指在结构中存在多余的支座或者杆件，使得结构的自由度小于零，即结构无法通过静力学方法求解。

在这种情况下，我们需要采用力法或者位移法来求解结构的内力和位移。

力法是指通过假设结构内力的大小和方向，来求解结构的内力和位移的方法。

在力法中，我们需要假设结构内力的大小和方向，然后通过平衡方程和变形方程来求解结构的内力和位移。

力法的优点是计算简单，适用于简单的结构，但是对于复杂的结构，力法的假设可能会导致误差较大。

位移法是指通过假设结构的位移，来求解结构的内力和位移的方法。

在位移法中，我们需要假设结构的位移，然后通过平衡方程和变形方程来求解结构的内力和位移。

位移法的优点是适用于复杂的结构，可以准确地求解结构的内力和位移，但是计算较为繁琐。

在实际工程中，我们通常采用力法和位移法相结合的方法来求解超静定结构。

首先，我们可以通过力法来确定结构的内力大小和方向，然后再通过位移法来求解结构的位移。

这种方法可以充分利用力法和位移法的优点，减小误差，提高计算精度。

超静定结构的求解需要采用力法和位移法相结合的方法，通过假设结构的内力和位移，来求解结构的内力和位移。

在实际工程中，我们需要根据具体情况选择合适的方法，以保证计算精度和效率。

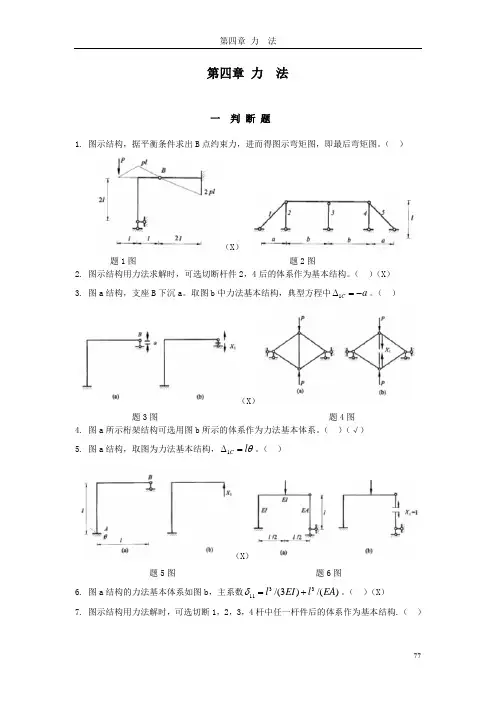
第四章 力 法一 判 断 题1. 图示结构，据平衡条件求出B 点约束力，进而得图示弯矩图，即最后弯矩图。

（ ）（X ）题1图 题2图2. 图示结构用力法求解时，可选切断杆件2，4后的体系作为基本结构。

（ ）（X ）3. 图a 结构，支座B 下沉a 。

取图b 中力法基本结构，典型方程中1C a ∆=-。

（ ） （X ）题3图 题4图4. 图a 所示桁架结构可选用图b 所示的体系作为力法基本体系。

（ ）（√）5. 图a 结构，取图为力法基本结构，1C l θ∆=。

（ ） （X ）题5图 题6图6. 图a 结构的力法基本体系如图b ，主系数3311/(3)/()l EI l EA δ=+。

（ ）（X ）7. 图示结构用力法解时，可选切断1，2，3，4杆中任一杆件后的体系作为基本结构.（ ）（X ）题7图 题9图 8. 图示结构受温度变化作用，已知α，h ，选解除支杆B 为力法基本体系(设B X 向上为正)，典型方程中自由项2121()/(4)t a t t l h ∆=--。

（ ）（X ）9. 图a 结构，力法基本体系如图b ，自由项412/(8)P ql EI ∆=-。

（ ）（X ）题10图 题11图10.图示超静定梁在支座转动1A ϕ=时的杆端弯矩26.310AB M KN m =⨯⋅，22( 6.310)EI KN m =⨯⋅。

（ ）（√） 11. 图a 结构，取图b 为力法基本结构，h 为截面高度，α为线胀系数，典型方程中2121()/(2)t a t t l h ∆=--。

（ ）（X ）题12图 题13图 12. 图a 结构，取力法基本体系如图b 所示，则1/C l ∆=∆（ ）。

（X ）13. 超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。

（ ）（√）14. 图示结构的超静定次数为4。

（ ）（X ）题15图 题16图15. 图示结构，选切断水平杆为力法基本体系时，其3112/(3)h EI δ=。

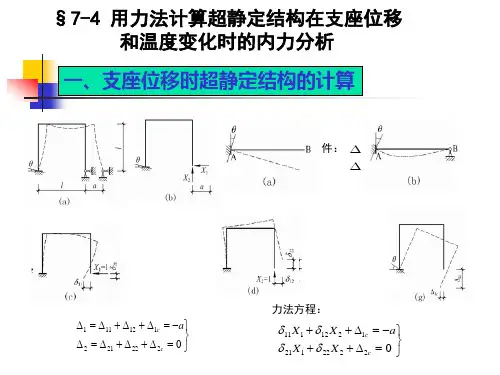
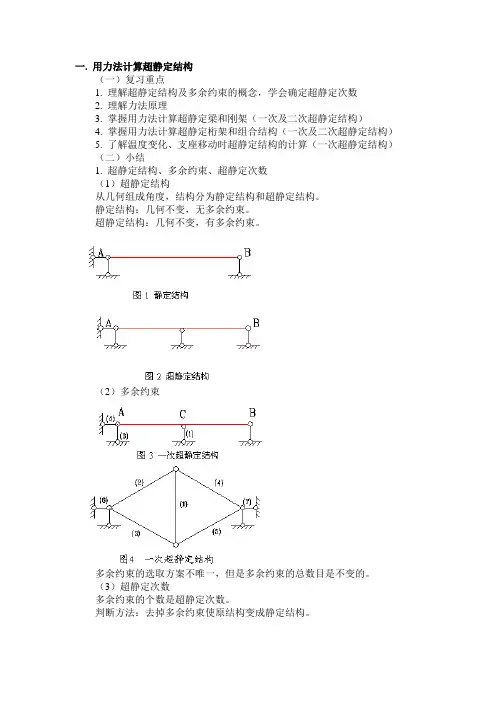
一. 用力法计算超静定结构（一）复习重点1. 理解超静定结构及多余约束的概念，学会确定超静定次数2. 理解力法原理3. 掌握用力法计算超静定梁和刚架（一次及二次超静定结构）4. 掌握用力法计算超静定桁架和组合结构（一次及二次超静定结构）5. 了解温度变化、支座移动时超静定结构的计算（一次超静定结构）（二）小结1. 超静定结构、多余约束、超静定次数（1）超静定结构从几何组成角度，结构分为静定结构和超静定结构。

静定结构：几何不变，无多余约束。

超静定结构：几何不变，有多余约束。

（2）多余约束多余约束的选取方案不唯一，但是多余约束的总数目是不变的。

（3）超静定次数多余约束的个数是超静定次数。

判断方法：去掉多余约束使原结构变成静定结构。

2. 力法原理力法是计算超静定结构最基本的方法（1）将原结构变为基本结构（2）位移条件：（3）建立力法方程3．用力法求解超静定梁和刚架例：二次超静定结构（1）原结构变为基本结构（2）位移条件（3）力法方程（3）绘弯矩图4. 用力法计算超静定桁架和组合结构注意各杆的受力特点：二力杆只有轴力，受弯杆的内力有弯矩、剪力和轴力。

例：超静定组合结构（1）原结构变为基本结构（2）位移条件（3）力法方程（4）绘弯矩图5. 了解温度变化、支座移动时超静定结构的内力计算（1）温度变化时，超静定结构的内力计算原结构变为基本结构位移条件力法方程（2）支座移动时，超静定结构的内力计算原结构变为基本结构位移条件二. 用位移法计算超静定结构（一）复习重点1. 了解位移法基本概念及位移法与力法的区别2. 掌握用位移法计算超静定结构（具有一个及两个结点位移）3. 掌握计算对称结构的简化方法（二）小结1. 了解位移法基本概念及位移法与力法的区别位移法是求解超静定结构的又一基本方法，适用于求解超静定次数较高的连续梁和刚架。

位移法的前提假设：对于受弯的杆件，可略去轴向变形和剪切变形的影响，2. 掌握用位移法求解超静定结构（具有一个及两个结点位移的结构）例：求连续梁的内力解：（1）确定基本未知量及基本体系基本未知量是结点B的角位移。

西工大2020年4月《结构力学》作业机考参考答案
试卷总分:100 得分:100
本作业试题内容相同，只是题目和选项顺序是随机调整的，大家可放心学习使用
一、单选题(共15 道试题,共30 分)
1.单刚节点相当于（）个约束。

A.1
B.2
C.3
D.4
正确答案:C
2.有关力法求解超静定的结构问题，下列说法正确的是（）。

A.力法的基本体系可用是瞬息变体系
B.静定结构可以用力法求解
C.超静定结构可以作为力法的基本体系
D.结构的超静定次数不一定等于多余约束个数
正确答案:D
3.两个刚片之间由四个连杆相连构成的体系是（）。

A.几何可变体系
B.无多余约束的几何不变体系
C.体系的组成不确定
D.有一个多余约束的几何不变体系
正确答案:C
4.超静定结构的计算，下列说法正确的是（）。

A.只需利用平衡条件
B.只需利用变形条件
C.既要考虑平衡条件，又要考虑变形条件
D.是否利用变形条件由荷载和结构构造情况决定
正确答案:C
5.静定结构因支座移动，（）。

A.会产生内力，但无位移
B.会产生位移，但无内力
C.内力和位移都不会产生
D.内力和位移都会产生
正确答案:B。

用 力 法 解 超 静 定 结 构 时 ，可 以 取 超 静 定 结 构 为 基 本 体 系 。

()力 法 只 能 用 于 线 性 变 形 体 系 。

()在 力 法 方 程δij j c i X ∑+=∆∆1 中 ：A B.C. D .;;;.∆∆∆i i i =><000前三种答案都有可能。

()力 法 方 程 是 沿 基 本 未 知 量 方 向 的 ：A ．力 的 平 衡 方 程 ；B ．位 移 为 零 方 程 ；C ．位 移 协 调 方 程 ；D ．力 的 平 衡 及 位 移 为 零 方 程 。

()力 法 方 程 中 柔 度 系 数 δi j 代 表，自由项∆i P代表。

力 法 方 程 等 号 左 侧 各 项 代 表，右 侧 代 表 。

图 b 为 图 a 用 力 法 求 解 时 所 用 基 本 体 系 ，则X 1 一 定 等 于 P /2 。

()X (a)(b)取 图 示 结 构 CD 杆 轴 力 为 力 法 的 基 本 未 知 量X 1 ，则 X 1= P ，各 杆 EA = 常 数 。

()图 a 结 构 取 力 法 基 本 未 知 量 X 1如 图 b ，则 力 法 方 程 中 ∆10P > 。

()D(a)(b)图 示 结 构 中 ，梁 AB 的 截 面 EI 为 常 数，各 链 杆 的E A 1相 同， 当 EI 增 大 时 ，则 梁 截 面 D 弯 矩 代 数 值M D 增 大 。

()C图 示 结 构，设 温 升 t t 12>， 则 支 座 反 力 R A 与R C 方 向 向 上，而 R B 必向 下 。

()+t +t 12B AEIEIC图 a 中 +t 为 温 升 值 ，-t 为 温 降 值 ，则 图 a 刚 架的 弯 矩 图 形 状 为 图 b 。

()(a)(b)-t+t-t图 示 结 构，当 B 支 座 下 沉 时 ，内 力 与 EI 绝 对 值 成 正 比 。

国家开放大学《土木工程力学（本）》章节测试参考答案1.绪论一、选择题1．图示支座形式可简化为（B）A. B. C. D.2．图示支座形式可简化为（D）A. B. C. D.3．刚结点在结构发生变形时的特征是()A.刚结点自身不会转动可任意改变B.结点处各杆端之间的夹角保持不变C.所联结的杆件可绕结点自由转动D.结点处各杆端之间的夹角可任意改变4．（）不允许结构在支承处发生任何方向的移动和转动A.固定支座B.定向支座C.活动铰支座D.固定铰支座5．（）不允许结构在支承处发生转动，也不能沿垂直于支承的方向移动，但可沿平行于支承的方向滑动A.固定铰支座B.活动铰支座C.固定支座D.定向支座6．（）只允许结构在支承处绕铰A转动，而不能发生任何移动A.固定铰支座B.固定支座C.活动铰支座D.定向支座7．（）只约束了支承链杆方向的位移，允许结构绕铰转动，也可沿着垂直于链杆的方向移动A.活动铰支座B.定向支座C.固定支座D.固定铰支座8．根据荷载的不同特征，荷载可分类，（）是指满布在结构或构件某部分面积上的荷载A.集中荷载B.分布荷载C.恒载D.静力荷载2.平面体系的几何组成分析一、选择题1．三刚片组成几何不变体系的规则是（）。

A.三铰三链杆相连，杆不通过铰B.三链杆相连，不平行也不相交于一点C.三铰两两相连，三铰不在一直线上D.一铰一链杆相连，杆不过铰2．在无多余约束的几何不变体系上增加二元体后构成（）。

A.有多余约束的几何不变体系B.无多余约束的几何不变体系C.瞬变体系D.可变体系3．对图示平面体系进行几何组成分析，该体系是（）。

A.瞬变体系B.无多余约束的几何不变体系C.有一个多余约束的几何不变体系D.几何可变体系4．对图示平面体系进行几何组成分析，该体系是（）。

A.有一个多余约束的几何不变体系B.无多余约束的几何不变体系C.瞬变体系D.几何可变体系5．对图示平面体系进行几何组成分析，该体系是（）。

A.瞬变体系C.有两个多余约束的几何不变体系D.有一个多余约束的几何不变体系6．对图2-27所示平面体系进行几何组成分析，该体系是（）。

力法、位移法求解超静定结构讲解超静定结构是指在静力学计算中具有过多约束的结构体系，其问题在于不能通过传统的静力学方法直接计算出结构体系的内力以及位移的分布情况，需要利用力法或者位移法来求解超静定结构。

力法是指将结构体系的内力分配给各个构件，然后根据各个构件的受力情况和变形情况，逐步推导出结构体系的内力和位移分布情况的一种方法。

其基本思想是通过外部荷载作用下的内力分配，将超静定结构分解成多个静定结构分析，同时通过协调各个分析时的界面条件，进行内力和位移的匹配，最终得到了超静定结构的内力和位移分布情况。

具体实现步骤如下：1. 选定一个自由图，并对该自由图进行划分，将超静定结构分成多个静定结构，其中每个静定结构的节点数均满足有一个自由度。

分割完毕后，确定每个静定结构的支座反力，然后由每个静定结构自己采用传统的静力学原理分析，并得到各自的内力和位移。

2. 对于静定结构之间的相互配合，需要根据结构体系的受力变形情况建立相互之间的协调关系。

最常用的协调方法是确定静定结构之间的界面条件，如节点位移和节点荷载的相等，以及弹簧刚度之和等于零。

3. 在确定了静定结构之间的界面条件后，就可以获得超静定结构的结构内力分布，接下来需要计算出结构的位移分布。

这一步可以通过位移影响系数法进行求解，具体来说，先在静定结构中确定一个位移分量，然后根据约束条件求得其余节点的位移分量，最终获得超静定结构的位移分布。

相比于力法，位移法的思路更加简洁明了，具体步骤如下：1. 建立超静定结构的初始刚度方程，包括构件中的整体刚度和节点位移自由度的边界条件等。

2. 将超静定结构受到的外载按照一定的规律进行分配，使得该结构从受力变形的点出发经过一系列刚度修正后，其总体刚度等于原结构的刚度。

这个修正过程是迭代的，一般采用迭代矩阵求逆的方式进行求解。

3. 当总体刚度修正后，结构的总位移就变为了一个已知量。

根据节点位移自由度的边界条件，可以直接解出各节点的位移分量。

一. 用力法计算超静定结构（一）复习重点1. 理解超静定结构及多余约束的概念，学会确定超静定次数2. 理解力法原理3. 掌握用力法计算超静定梁和刚架（一次及二次超静定结构）4. 掌握用力法计算超静定桁架和组合结构（一次及二次超静定结构）5. 了解温度变化、支座移动时超静定结构的计算（一次超静定结构）（二）小结1. 超静定结构、多余约束、超静定次数（1）超静定结构从几何组成角度，结构分为静定结构和超静定结构。

静定结构：几何不变，无多余约束。

超静定结构：几何不变，有多余约束。

（2）多余约束多余约束的选取方案不唯一，但是多余约束的总数目是不变的。

（3）超静定次数多余约束的个数是超静定次数。

判断方法：去掉多余约束使原结构变成静定结构。

2. 力法原理力法是计算超静定结构最基本的方法（1）将原结构变为基本结构（2）位移条件：（3）建立力法方程3．用力法求解超静定梁和刚架例：二次超静定结构（1）原结构变为基本结构（2）位移条件（3）力法方程（3）绘弯矩图4. 用力法计算超静定桁架和组合结构注意各杆的受力特点：二力杆只有轴力，受弯杆的内力有弯矩、剪力和轴力。

例：超静定组合结构（1）原结构变为基本结构（2）位移条件（3）力法方程（4）绘弯矩图5. 了解温度变化、支座移动时超静定结构的内力计算（1）温度变化时，超静定结构的内力计算原结构变为基本结构位移条件力法方程（2）支座移动时，超静定结构的内力计算原结构变为基本结构位移条件二. 用位移法计算超静定结构（一）复习重点1. 了解位移法基本概念及位移法与力法的区别2. 掌握用位移法计算超静定结构（具有一个及两个结点位移）3. 掌握计算对称结构的简化方法（二）小结1. 了解位移法基本概念及位移法与力法的区别位移法是求解超静定结构的又一基本方法，适用于求解超静定次数较高的连续梁和刚架。

位移法的前提假设：对于受弯的杆件，可略去轴向变形和剪切变形的影响，且弯曲变形是微小的，假定受弯杆件两端的距离在变形后保持不变。