超静定计算

1、超静定结构的特性：与静定结构比较，超静定结构有如下特性：内力超静定，约束有多余，是超静定结构区别于静定结构的基本特点。

2、超静定次数的确定：结构的超静定次数为其多余约束的数目，因此上，结构的超静定次数等于将原结构变成静定结构所去掉多余约束的数目。

在超静定结构上去掉多余约束的基本方式，通常有如下几种：（1）断一根链杆、去掉一个支杆、将一刚接处改为单铰联接、将一固定端改为固定铰支座，相当于去掉一个约束。

举例（2）断一根弯杆、去掉一个固定端，相当于去掉三个约束。

举例（3）开一个单铰、去掉一个固定铰支座、去掉一个定向支座，相当于去掉两个约束。

举例返回顶部3、几点注意：①由图10-1结构的分析可得出结论：一个无铰闭合框有三个多余约束，其超静定次数等于三。

对于无铰闭合框结构其超静定次数=3×闭合框数。

如图10-2所示结构的超静定次数为3×5=15次；对于带铰闭合框结构其超静定次数=3×闭合框数－结构中的单铰数（复铰要折算成单铰）如图10-3所示结构的超静定次数为3×5-（1+1+3）=15次。

D点是连接四个刚片的复铰，相当于（4-1）=3个单铰。

②一结构的超静定次数是确定不变的，但去掉多余约束的方式是多种多样的。

如图10-1结构。

③在确定超静定次数时，要将内外多余约束全部去掉。

如图10-4结构外部1次超静定，内部6次超静定，结构的超静定次数是7。

④在支座解除一个约束，用一个相应的约束反力来代替，在结构内部解除约束，用作用力和反作用力一对力来代替。

如图10-1结构所示。

⑤只能去掉多余约束，不能去掉必要的约束，不能将原结构变成瞬变体系或可变体系。

如图10-4结构中A点的水平支杆不能作为多余约束去掉。

如图10-5结构中支杆a,b和链杆c不能作为多余约束去掉，否则就将原结构变成了瞬变体系。

返回顶部1、超静定结构的求解思路：欲求解超静定结构，先选取一个便于计算结构作为基本体系，然后让基本体系与原结构受力一致，变形一致即完全等价，通过这个等价条件去建立求解基本未知量的基本方程。

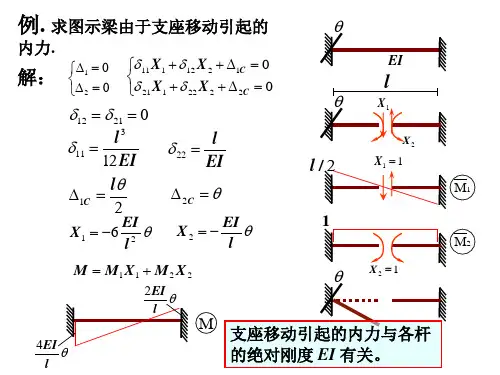
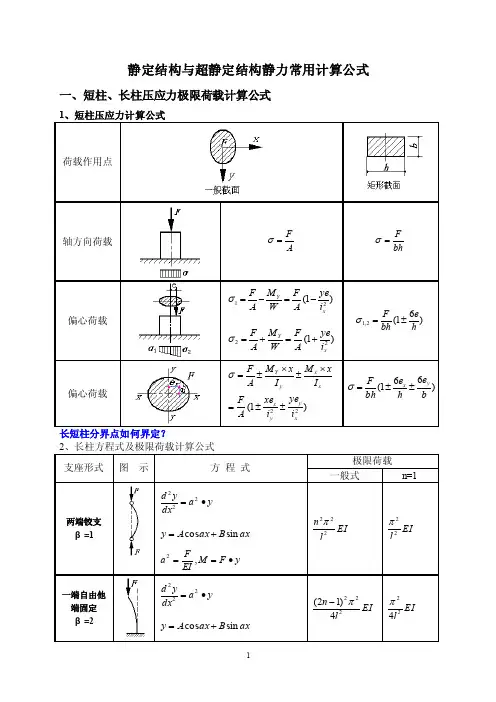
静定结构与超静定结构静力常用计算公式一、短柱、长柱压应力极限荷载计算公式1、短柱压应力计算公式荷载作用点轴方向荷载AF =σ bhF =σ 偏心荷载)1(21xY i ye A F W M A F -=-=σ )1(22xY i ye A F W M A F +=+=σ )61(2,1hebh F ±=σ 偏心荷载)1(22xy y x xx y Y i ye i xe A FI xM I x M A F ±±=⨯±⨯±=σ )661(beh ebh F yx ±±=σ长短柱分界点如何界定？2、长柱方程式及极限荷载计算公式 支座形式图 示方 程 式极限荷载 一般式 n=1两端铰支 β=1y a dxy d ∙=222 ax B ax A y sin cos +=y F M EIFa ∙==,2 EI ln 222π EI l 22π一端自由他端固定β=2y a dxyd ∙=222 ax B ax A y sin cos +=EI l n 2224)12(π-EI l 224πy F M EIFa ∙==,2 两端固定 β=0.50)(22=-+F M y a dxyd A FM ax B ax A y A++=sin cos A M y F M EIFa +∙-==,2 EI l 224π EI l 224π 一端铰支他端固定 β=0.75)(222x l EI Q y a dx y d -=∙+)(sin cos x l FQax B ax A y -++=水平荷载-=Q EIFa ,2 ——EI l227778.1π注：压杆稳定临界承载能力计算公式：EI l P cr 22)(βπ=二、单跨梁的反力、剪力、弯矩、挠度计算公式 1、简支梁的反力、剪力、弯矩、挠度计算公式荷载形式M 图V 图反力 2F R R B A == L Fb R A =L Fa R B =2qL R R B A == 4qL R R B A == 剪力V A =R A V B =-R B V A =R A V B =-R B V A =R A V B =-R BV A =R A V B =-R B弯矩4max FL M =LFabM =max 82maxqL M = 122maxqL M = 挠度EIFL 483max=ω 若a ＞b 时，3)2(932maxab a EIL Fb +=ω（在)2(3b a ax +=处） EIqL 84max=ω EIqL 1204max=ω 注：1、弯矩符号以梁截面下翼缘手拉为正（+），反之为负（—）。

计算结构超静定次数的公式
结构超静定次数（SDOF，即单自由度系统）是一种描述动力学特性的重要工程
物理指标，它是对结构特性的重要衡量指标，也是在设计结构时明确可能受到的外力的一种有用的参考。

由于结构超静定次数的重要性，因此非常重要的就是计算每个结构的SDOF，即计算结构超静定次数的公式。

一般情况下，结构超静定次数的公式可分为定位法和统计法。

定位法的公式是：SDOF= 1/k+1/c+1/m，这里K为模态弹性系数，C为模态阻尼系数，M为模态质量系数。

统计法的公式涉及谱强度概率计算等方法，是一种自动计算方式，该方法可以精确地表达自动除去局部谐振的自激阻尼的系统的超静定次数，从而得出结构超静定次数。

尽管定位法和统计法都具有计算精确、效率高的优势，但由于计算结构超静定
次数时涉及模态参数摸索和较为复杂的反向计算，所以在实施计算过程中往往需要考虑多个利益相关方的功能要求，以便在整个过程中取得最优折中结果。

因此，在实际应用中，一般更合理采用可靠的统计法，以得出满足实际要求的最优超静定次数。

总的来说，结构超静定次数的公式不仅对合理设计结构十分重要，也为了保证
在极端情况下结构的可靠性而设计有重要意义。

因此，在实施结构设计时应首先确定结构超静定次数，以保证结构稳定，安全可靠。

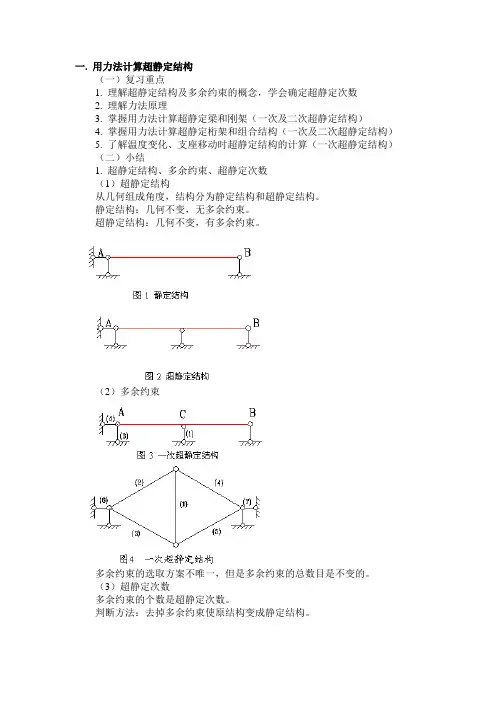
一. 用力法计算超静定结构（一）复习重点1. 理解超静定结构及多余约束的概念，学会确定超静定次数2. 理解力法原理3. 掌握用力法计算超静定梁和刚架（一次及二次超静定结构）4. 掌握用力法计算超静定桁架和组合结构（一次及二次超静定结构）5. 了解温度变化、支座移动时超静定结构的计算（一次超静定结构）（二）小结1. 超静定结构、多余约束、超静定次数（1）超静定结构从几何组成角度，结构分为静定结构和超静定结构。

静定结构：几何不变，无多余约束。

超静定结构：几何不变，有多余约束。

（2）多余约束多余约束的选取方案不唯一，但是多余约束的总数目是不变的。

（3）超静定次数多余约束的个数是超静定次数。

判断方法：去掉多余约束使原结构变成静定结构。

2. 力法原理力法是计算超静定结构最基本的方法（1）将原结构变为基本结构（2）位移条件：（3）建立力法方程3．用力法求解超静定梁和刚架例：二次超静定结构（1）原结构变为基本结构（2）位移条件（3）力法方程（3）绘弯矩图4. 用力法计算超静定桁架和组合结构注意各杆的受力特点：二力杆只有轴力，受弯杆的内力有弯矩、剪力和轴力。

例：超静定组合结构（1）原结构变为基本结构（2）位移条件（3）力法方程（4）绘弯矩图5. 了解温度变化、支座移动时超静定结构的内力计算（1）温度变化时，超静定结构的内力计算原结构变为基本结构位移条件力法方程（2）支座移动时，超静定结构的内力计算原结构变为基本结构位移条件二. 用位移法计算超静定结构（一）复习重点1. 了解位移法基本概念及位移法与力法的区别2. 掌握用位移法计算超静定结构（具有一个及两个结点位移）3. 掌握计算对称结构的简化方法（二）小结1. 了解位移法基本概念及位移法与力法的区别位移法是求解超静定结构的又一基本方法，适用于求解超静定次数较高的连续梁和刚架。

位移法的前提假设：对于受弯的杆件，可略去轴向变形和剪切变形的影响，2. 掌握用位移法求解超静定结构（具有一个及两个结点位移的结构）例：求连续梁的内力解：（1）确定基本未知量及基本体系基本未知量是结点B的角位移。

六超静定结构內力计算1．什么是超静定结构？它和静定结构有何区别？答：单靠静力平衡条件不能确定全部反力和內力的结构为超静定结构。

从几何组成的角度看，静定结构是没有多余约束的几何不变体系。

若去掉其中任何一个约束，静定结构即成为几何可变体系。

也就是说，静定结构的任何一个约束，对维持其几何不变性都是必要的，称为必要约束。

对于超静定结构，若去掉其中一个甚至多个约束后，结构仍可能是几何不变的。

2．什么是超静定结构的超静定次数？答：超静定结构多余约束的数目，或者多余约束力的数目，称为结构的超静定次数。

3．超静定结构的基本结构是否必须是静定结构？答：超静定结构的基本结构必须是静定结构。

4．如何确定超静定结构的超静定次数？答：确定结构超静定次数的方法是：去掉超静定结构的多余约束，使之变为静定结构，则去掉多余约束的个数，即为结构的超静定次数。

5．撤除多余约束的方法有哪几种？答：撤除多余约束常用方法如下：（1）去掉一根支座链杆或切断一根链杆，等于去掉一个约束。

（2）去掉一个固定铰支座或拆去一个单铰，等于去掉两个约束。

（3）去掉一个固定端支座或把刚性连接切开，等于去掉三个约束。

6．用力法计算超静定结构的基本思路是什么？答：用力法计算超静定结构的基本思路是：去掉超静定结构的多于约束，代之以多余未知力，形成静定的基本结构；取多余未知力作为基本未知量，通过基本结构的位移谐调条件建立力法方程，利用这一变形条件求解多余约束力；将已知外荷载和多余约束力所引起的基本结构的内力叠加，即为原超静定结构在荷载作用下产生的内力。

7．什么是力法的基本结构和基本未知量？答：力法的基本结构是：超静定结构去掉多余约束后得到的静定结构。

力法的基本未知量是对应于多余约束的约束反力。

8．简述n次超静定结构的力法方程，及求原结构的全部反力和內力的方法。

答：（1）n次超静定结构的力法方程对于n次超静定结构，撤去n个多余约束后可得到静定的基本结构，在去掉的n个多余约束处代以相应的多余未知力。