下载文档原格式
2019年七年级下册数学单元测试题第七章 分式一、选择题1．小明通常上学时走上坡路，途中的速度为m 千米/时，放学回家时，沿原路返回，速度为n 千米/时，则小明上学和放学路上的平均速度为（ ）A ．2nm +千米/时 B ．n m mn +千米/时 C ．n m mn +2千米/时 D ．mnnm +千米/时 解析：C2．当2x =-时，分式11x+的值为（ ） A ．1B ．-1C ．2D ．-2答案：B3．把分式xx y+（0x ≠，0y ≠）中的分子，分母的x ，y 同时扩大 2倍.那么分式的值（ ） A ．扩大2倍 B ． 缩小2倍 C ． 改变原来的值 D ． 不改变答案：D4．若有m 人，a 天可完成某项工作，则（m n +）人完成此项工作的天数是（ ） A ．a m +B ．amm n+ C ．am n+ D ．m nam+ 答案：B5．x （g ）盐溶解在 a （g ）水中，取这种盐水m （g ），含盐（ ） A ．mxa（g ） B ．amx（g ） C ．amx a+（g ） D ．mxx a+（g ） 答案：D6． 一组学生去春游，预计共需费用 120 元，后来又有 2 个同学参加进来，总费用不 变，于是每人可少分摊 3 元，原来这组学生的人数是（ ） A ．8 人B ．10人C ． 12人D ． 30 人答案：A7．“a 和b 的平方的和除以c ”可表示为（ ）A ．2()a b c+B ．2b ac +C ．22a b c+D ． 2a b c+答案：D8．用x -代替各式中的x ，分式的值不变的是（ ）A ．32xB ．3x-C ．21xx + D ．211x -+ 答案：D9．方程x 3＝22-x 的解的情况是（ ）A ．2=xB ．6=xC ．6-=xD ．无解答案：B10．与分式2xy的值相等的是（ ） A ．222x y ++B ．63x yC ．3(2x)yD ．2x y- 答案：B11． 已知分式11+-x x 的值是零，那么x 的值是（ ） A ．-1B ．0C ．1D ． 1±答案：C12．下列分式中是最简分式的是（ ）A ．122+x x B ．x24C ．112--x xD ．11--x x答案：A13．“5·12”汶川大地震导致某铁路隧道被严重破坏．为抢修其中一段120米的铁路，施工队每天比原计划多修5米，结果提前4天开通了列车．问原计划每天修多少米？设原计划每天修x 米，所列方程正确的是（ ）A ．12012045x x -=+ B ．12012045x x -=+ C ．12012045x x -=-D ．12012045x x -=-解析：B14．1a a a+⋅的结果是（ ） A ．1a +B ．2C ．2aD ．1答案：A15．方程512552x x x+=--的解x 等于（ ） A ．-3B ．-2C ． -1D ．0答案：D16．某种商品在降价x %后，单价为a 元，则降价前它的单价为（ ） A ．%a x B ．%a x ⋅C ．1%ax -D ．(1%)a x -答案：C17．如果分式-23x -的值为负，则x 的取值范围是（ ） A ．x>2B ．x>3C ．x<3D ．x<2答案：B 二、填空题18．若2a a b =+，当a 、b 都扩大到原来的2009倍时，aa b+的值怎样变化？(填“变大”、“变小”或“不变”) . 解析：不变 19．若分式27xx -无意义，则x 的值为 . 解析：3.520． 甲、乙两人分别从相距s(km)的A ，B 两地同时出发，相向而行，已知甲的速度是每小时m(krn)，乙的速度是每小时n(km)，则经过 h 两人相遇.解析：nm s+ 21．当x ________时，分式xx2121-+有意义． 解析：21≠22．轮船在静水中每小时行驶akm ，水流的速度为每小时bkm ，则轮船在逆流中行驶skm 需要 小时. 解答题解析：ba s -23．当x 时，分式12x x --有意义；当x= 时，12x x --的值为零. 解析：2≠ ，124．如果分式211x x -+的值为0，则x= .解析：125．已知关于x 的分式方程4333k x x x-+=--有增根，则k 的值是 ． 解析：1 26．若543222Ax B x x x x x --=-+++，则A= ，B= ． 解析： 1,-327．小舒 t(h)走了 s(km)的路程，则小舒走路的平均速度是 km/h.解析：s t28．将下列代数式按要求分类：a ，1x ，15，223x x --，239x y +，213x x +，234a b π．整式： ； 分式： ．解析：a ，15，239x y +，234a b π；1x ，223x x --，213xx +29．不改变分式的值. 使分子、分母都不含不含负号： (1)23x -= ；(2)x yz -- = ；(3)2ab ---；(4)5yx--- = ．解析： (1)23x -；(2)x yz ；(3)2ab -；(4)5y x+三、解答题30．请观察下列方程和它们的根： 1112x x -=，12x =，212x =-；1223x x -=，13x =，213x =-； 1334x x -=，14x =，214x =-；1445x x -=，15x =，215x =-； …(1)请你猜想第 10 个方程1101011x x -=的根是 ；(2)猜想第n 个方程是什么？它的根是什么？并将你猜想的原方程的根代人方程检验.解析：（1）111x =，2111x =-；（2）11n x n x n -=++，11x n =+，211x n =-+，检验略 31．当 x 取什么值时，下列分式的值为零？ (1)1510x x +-；（2）211x x -+；（3）||22x x --解析： (1)1x =-；（2）1x =；（3）2x =-32．当3x =时，分式301x kx -=-，求k 的值. 9k =解析：9k =33．某校有学生 2500 人，每个学生平均每天用水 a(kg)，在该校提倡“人人节水”之后，如果每个学生平均每天节约用水 1 kg ，那么 A(kg)水可供全校用多少天？当 A=7500000，a=4 时，可供全校用多少天？解析：2500(1)Aa -天，1000 天34．先化简，再求值：(1)21()a a a a-÷-，其中a = (2)22142244a a a a a --⨯--+，其中1a =-．解析： (1)21a，13；(2)22(2)a a +-，16- 35．有这样一道题“计算：2222111x x x x x x x-+-÷--+的值，其中2008x =．”甲同学把“2008x =”错抄成“2080x =”，但他的计算结果也正确，这是怎么回事？解析： 原式的值为 0，与x 值无关 36．计算：(1）22(2)(3)33321x x x x x x x x ----÷⋅--+；（2）2222()(2)x y x y x xy y xy -÷-÷++ (3)222222422x 2x y x y x yx y x xy y x xy-+-÷÷++++解析： (1)3x ；(2)221x y xy +；(3)137．计算：(1)432114212121a a aa a a +----+++；(2)2242n mn m mn m n m n n m ------；(3)22()()()()xy yz x y x z x y z x +----； (4)2b a c b ca b c b a c b a c+-+--+----解析：（1）3；（2）m n -；(3)2yyχ-；(4)-2 38．把甲、乙两种原料按 a ： b 的质量比混合(a>b)，调制成一种混合饮料，要调制4 kg 这种混合饮料，需要的甲原料比乙原料多多少？ (用含 a ，b 的代数式表示) 44a ba b-+ 解析：44a ba b-+ 39．将分式10(2)(1)(2)(1)(1)x x x x x +++-+约分，再讨论x 取哪些整数时，能使分式的值是正整数.解析：101x -，当 x=2或3 或6或 11 40．已知123x x +=，121x x =． (1)求1211x x +的值； (2)求2112x x x x +的值； (3)求2112111+1x x x x ++++的值.解析： (1)3；(2)7；(3)341．先化简，再选择使原式有意义而且你喜欢的数代入求值：22315313695x x x x x x x +-⋅---++.解析：化简结果为1x-，计算结果与代入的x 的值有关，答案不唯42．为了帮助受灾地区重建家园，某中学团委组织学生开展献爱心活动. 已知第一次捐 款为 4800 元，第二次捐款为 5000 元，第二次捐款人数比第一次多 20 人，两次人均捐款教相等. 问第一次有多少人捐款？解析：480人43．某工厂去年赢利 25 万元，按计划这笔赢利额应是去年和今年赢利总额的 20%，设今年的赢利额是x 万元，请你写出 x 满足的方程. 你能写出几个方程？其中哪一个是分式方程？解析： 方程（1）：252025100x =+；方程（2）20(25)25100x +⨯=；方程（3）：252520%x +=÷．方程（1）是分式方程44．为加快西都大开发，某自治区决定新修一条公路，甲、乙两工程队承包此项工程. 如 果甲工程队单独施工，则刚好如期完成；如果乙工程队单独施工就要超过 6 个月才能完成. 现在甲、乙两队先共同施工 4个月，剩下的由乙队单独施工，则刚好如期完成. 问原来规定修好这条公路需多长时间？解析：12 个月45．先化简)11(122xx x x -⋅-+，然后自选一个你喜欢的x 值，求原式的值．解析：化简得：2+x ，但x 不能取0和1． 46．设23111x A B x x ==+--，，当x 为何值时，A 与B 的值相等？解析：当2x =时，A B =．47．有一道题“先化简，再求值：22241244x x x x x -+÷+--（），其中x =时把“x =x =回事？解析：222222241444(4)42444x x x x x x x x x x x --+++÷=⨯-=++---（），因为x =x =2x 的值均为3，原式的计算结果都是7，所以把“x =x =48．甲、乙两工程队分别承担一条2千米公路的维修工作，甲队有一半时间每天维修公路x 千米，另一半时间每天维修公路y 千米．乙队维修前1千米公路时，每天维修x 千米；维修后1千米公路时，每天维修y 千米(x ≠y )．⑴求甲、乙两队完成任务需要的时间(用含x 、y 的代数式表示)； ⑵问甲、乙两队哪队先完成任务？解析：(1)甲、乙两队完成任务需要的时间分别为y x +4与xyyx +； (2) y x +4-xyy x +=0)()(2<+--y x xy y x （x ≠y ）,∴甲队先完成49．城北区在一项市政工程招标时，接到甲、乙工程队的投标书：每施工一天，需付甲工程队工程款为 1.5万元，付乙工程队1. 1万元. 工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：(方案一)甲队单独施工完成此项工程刚好如期完工； (方案二)乙队单独施工完成此项工程要比规定工期多用5天；(方案三)若甲、乙两队合作4天，剩下的工程由乙队独做也正好如期完工. 你认为哪一种施工方案最节省工程款？解析：设甲队单独施工完成此项工程需x 天，则乙需（5x +)天，根据题意，得415xx +=+， 解得20x =，经检验，20x =是原方程的根. 方案一所需工程款为 20×1.5=30(万元)； 方案二需工程款为 25x1.1=27.5(万元)； 方案三所需工程款为 4×1.5+20×1.1=28(万元). 所以方案二最省工程款50．将下面的代数式尽可能化简，再选择一个你喜欢的数代入求值：212(1)1a a a a --++-．解析：2a ，所得的值不唯一。
2019年七年级下册数学单元测试题第七章 分式一、选择题1．如果3x y =，那么分式222xyx y +的值为（ ） A ． 35B ．53C ．6D ． 不能确定答案：A2．用x -代替各式中的x ，分式的值不变的是（ ） A ．32x B ．3x- C ．21xx + D ．211x -+ 答案：D3．把分式xx y+（0x ≠，0y ≠）中的分子，分母的x ，y 同时扩大 2倍.那么分式的值（ ） A ．扩大2倍 B ． 缩小2倍 C ． 改变原来的值 D ． 不改变答案：D4．若有m 人，a 天可完成某项工作，则（m n +）人完成此项工作的天数是（ ） A ．a m +B ．amm n+ C ．am n+ D ．m nam+ 答案：B5．下列各式运算正确的是（ ） A ．0c d c da a-+-= B ．0a ba b b a-=-- C ．33110()()a b b a +=-- D ．22110()()a b b a +=--答案：C6． 已知222220a a b b ++++=，则1ba+的值是（ ）A ．2B ．1C ．0D ．-1答案：A7．某中学八年级甲、乙两班学生参加植树造林，已知甲班每天比乙班多植 5 棵树，甲班植 80 棵树所用的天数与乙班植 70 棵树所用的天数相等.若设甲班每天植树x 棵，则根据题意列出的方程是（ ） A ．80705x x=- B ．80705x x =+ C ．80705x χ=+ D ．80705x x =- 答案：D8．某人往返于A 、B 两地，去时先步行2公里再乘汽车10公里；回来时骑自行车，来去所用时间恰好一样，已知汽车每小时比步行多走16公里，自行车比步行每小时多走8公里，若步行速度为x 公里/小时，则可列出方程（ ） A ．21210816xx x +=++B ．10122168x x x -=++C ．21012168x x x +=++D ．10122168x x x+=++解析：Ｃ9．赵强同学借了一本书，共 280 页，要在两周借期内读完. 当他读了一半时，发现平均每天要多读 21 页才能在借期内读完. 他读前一半时，平均每天读多少页？如果设读前一 半时，平均每天读x 页，则下列方程中，正确的是（ ） A ．1401401421x x +=- B ．2802801421x x +=+ C ．1401401421x x +=+ D ．1010121x x +=+ 答案：C10．若关于x 的方程652mx =-的根为 1，则m 等于（ ） A ． 1B ． 8C ．18D ． 42答案：C11． 一组学生去春游，预计共需费用 120 元，后来又有 2 个同学参加进来，总费用不 变，于是每人可少分摊 3 元，原来这组学生的人数是（ ） A ．8 人B ．10人C ． 12人D ． 30 人答案：A12．已知111a b a b +=+，则b aa b+的值为（ ）A ．1B ．0C ．-1D ．-2解析：Ｃ13．分式方程11888x x x +=+--的根是（ ）A ．x=8B ．x=1C ．无解D ．有无数多个解析：Ｃ 14．解分式方程4223=-+-xxx 时，去分母后得（ ） A ．)2(43-=-x x B ．)2(43-=+x xC ．4)2()2(3=-+-x x xD ．43=-x答案：A15．若关于x 的方程1011--=--m xx x 有增根，则m 的值是（ ） A ．3B ．2C ．1D ．－1答案：B16．下列各式与x yx y-+相等的是（ ） A ．55x y x y -+++B ． 22x y x y-+C ．222()x y x y --（x y ≠）D ．2222x y x y-+ 答案：C17．若分式3242x x +-有意义，则字母x 的取值范围是（ ） A ．12x =B ．23x =-C ．12x ≠23x ≠- 答案：C18．在公式12111R r r =+（120r r +≠）中，用1r ，2r 表示R 的式子是（ ） A ．12R r r =+ B ．12R r r =C ．1212r r R r r +=D ．1212r r R r r =+ 答案：D 二、填空题19．当2x =时，分式301x kx -=+，则2k += . 解析：8 20．代数式1x 、a 、2π、2x 13-、2y x y -中， 是整式，_ 是分式.解析：a ，2π，213x -；1x，2y x y -21．若14-m 表示一个正整数，则整数m 的值为 ． 解析：2，3，522．当x ________时，分式xx2121-+有意义． 解析：21≠23．请选择一组,a b 的值，写出一个关于x 的形如2ab x =-的分式方程，使它的解是0x =，这样的分式方程可以是____________．解析：如212x -=-（答案不唯一）24．一根蜡烛在凸透镜下成一实像，物距u ，像距v 和凸透镜的焦距f 满足关系式：1u ＋1v ＝1f．若f ＝6厘米，v ＝8厘米，则物距u ＝________厘米． 解析：2425．当x=1,2y=-1时，分式3x y xy -的值是 . 解析：-726．下面是一个有规律的数表：上面数表中第 9 行、第 7 列的数是 ，第 (n+1)行、第 (n +2)列的数是 ． 解答题 解析：97，12n n ++ 27．如果543a +与23a -互为倒数，那么a = ． 解析：3 28．若分式方程244x ax x =+--有增根，则a 的值为 ． 解析：429．小舒 t(h)走了 s(km)的路程，则小舒走路的平均速度是 km/h.解析：st30．某工厂要生产 a 个零件，原计划每天生产 x 个，后来由于供货需要，每天多生产 b 个零件，则可提前 天完成.解析：a a x x b-+ 31．已知甲工人每小时能加工零件a 个，现总共有零件A 个.(1)甲工人加工 t(h)能完成 个零件，若全部完成这批零件，则需要 h ；(2)已知乙工人每小时能加工零件 b 个，若乙工人也来加工这批零件，则两人同时开始加工零件，需要 h 才能完成，比甲独做提前 h. 解析：（1） (1)at ，A a ；（2）A a b +，A A a a b-+ 32．在括号内填上适当的代数式，使等式成立. (1)()b a a a +=-；(2)322323()y x x y y x --=-；(3)216()324ab a a =；(4)39()()x x x y x y +=+解答题解析： (1)a b --；(2)32x y -；(3)2b ；(4)23()x y +三、解答题33．化简并求值：22222244x y x y x y x xy y --÷-+++，其中2x =2y =解析：xx y -+，34．先约分，再求值： (1)22444x x x --+，其中3x =． (2) 222x x y xy--，其中2x =-，2y =解析： (1)22x x +-，5 ； (2)x y -，135．下列各个分式中的字母满足什么条件时，分式有意义？ (1)251y -；(2)1|1|a -；(3)1||1b -解析：（1）1y ≠±；（2）1a ≠；（3）1b ≠±36．轮船在静水中每小时航行 a(m)，水流速度是每小时 b(km)，则该轮船在顺水中航行s(km)需要多少时间？ s a b+ 解析：s a b+37．先化简，再求值：(1)21()a a a a-÷-，其中a = (2)22142244a a a a a --⨯--+，其中1a =-．解析： (1)21a，13；(2)22(2)a a +-，16- 38．计算：(1)22x x x x --⋅-；(2)212(8)5xy a y a÷-；(3)2(1)(2)2(1)(1)a a a a a a -+⋅++-；(4)22211444a a a a a --÷-+-； (5)2b c c ax ax x⋅÷；(6)222()a b ab b a b --÷+解析： (1)1；(2)3310x a -；(3)21a a a -+；(4)2(2)(1)a a a +-+；(5)2ba ；(6)b39．计算：(1）22(2)(3)33321x x x x x x x x ----÷⋅--+；（2）2222()(2)x y x y x xy y xy -÷-÷++ (3)222222422x 2x y x y x yx y x xy y x xy-+-÷÷++++解析： (1)3x ；(2)221x y xy +；(3)140．化简下列各分式：(1)236sxy x y-； (2) 22699x x x -+-解析：（1）22y x -；(2)33x x -+41．把甲、乙两种原料按 a ： b 的质量比混合(a>b)，调制成一种混合饮料，要调制4 kg 这种混合饮料，需要的甲原料比乙原料多多少？ (用含 a ，b 的代数式表示) 44a ba b-+解析：44a b a b-+42． 在学完“分式”这一章后，老师布置了这样一道题：“先化简再求值： 22241()244x x x x x -+÷+--，其中2x =-”. 婷婷做题时把“2x =-”错抄成了“2x =”，但她的计算结果是正确的，请你通过计算解释其中的原因.解析：化简结果为24x +，当2x =-或2x =时，代入求得的值都是843．一架飞机从北京到上海一个来回，在有风(顺、逆风)和无风的时候，哪种情况更快？解析： 有风时飞行时间较长 44．请观察下列方程和它们的根： 1112x x -=，12x =，212x =-；1223x x -=，13x =，213x =-； 1334x x -=，14x =，214x =-；1445x x -=，15x =，215x =-； …(1)请你猜想第 10 个方程1101011x x -=的根是 ；(2)猜想第n 个方程是什么？它的根是什么？并将你猜想的原方程的根代人方程检验.解析：（1）111x =，2111x =-；（2）11n x n x n -=++，11x n =+，211x n =-+，检验略 45．某工厂去年赢利 25 万元，按计划这笔赢利额应是去年和今年赢利总额的 20%，设今年的赢利额是x 万元，请你写出 x 满足的方程. 你能写出几个方程？其中哪一个是分式方程？解析： 方程（1）：252025100x =+；方程（2）20(25)25100x +⨯=；方程（3）：252520%x +=÷．方程（1）是分式方程 46．分式方程0111x k x x x x +-=--+有增根x=1，求k 的值．解析：1-=k ． 47．化简： (1）21211x x x ++- (2）1)111(-÷--x xx解析：（1）11x-，（2）1． 48． 请从下列三个代数式中任选两个构成一个分式，并化简该分式. ｘ2－4ｘｙ＋4ｙ2ｘ2－4ｙ2ｘ－2ｙ解析：解:2222444yx y xy x -+- =)2)(2()2(2y x y x y x -+-=y x y x 22+- . (答案不惟一）49．有一道题“先化简，再求值：22241244x x x x x -+÷+--（），其中x =时把“x =x =回事？解析：222222241444(4)42444x x x x xx x x x x x --+++÷=⨯-=++---（），因为x =x =2x 的值均为3，原式的计算结果都是7，所以把“x =x =50．一个长，宽，高分别为 a ，b ，h 的长方体烟盒内装满了高为h 的香烟，共 20 枝. 打开烟盒盖，20 支香烟排成三行(如图所示). 求烟盒的空间利用率. (已知 2.56ab=，π取 3. 14，结果精确到 1%，烟盒纸厚度忽略不计)解析： 约 82%。
1. 一老人60岁时将养老金10万元存入基金会，月利率0.4%， 他每月取1000元作为生活费，建立差分方程计算他每岁末尚有多少钱？多少岁时将基金用完？如果想用到80岁，问60岁时应存入多少钱？分析：(1) 假设k 个月后尚有k A 元，每月取款b 元，月利率为 r ，根据题意，可每月取款，根据题意，建立如下的差分方程：1k k A aA b +=-，其中a = 1 + r (1)每岁末尚有多少钱,即用差分方程给出k A 的值。
(2) 多少岁时将基金用完，何时0k A =由（1）可得：01kkk a A A a br-=-若0n A =，01nnA rab a =-(3) 若想用到 80 岁，即 n ＝(80-60)*12=240 时，2400A =，24002401A ra b a=-利用 MA TLAB 编程序分析计算该差分方程模型，源程序如下： clear all close allclcx0=100000;n=150;b=1000;r=0.004; k=(0:n)';y1=dai(x0,n,r,b); round([k,y1'])function x=dai(x0,n,r,b) a=1+r; x=x0;for k=1:nx(k+1)=a*x(k)-b; end(2)用MA TLAB 计算：A0=250000*(1.004^240-1)/1.004^240思考与深入：(2) 结论：128个月即70岁8个月时将基金用完(3) A0 = 1.5409e+005结论：若想用到80岁，60岁时应存入15.409万元。
2. 某人从银行贷款购房，若他今年初贷款10万元，月利率0.5%，他每月还1000元。
建立差分方程计算他每年末欠银行多少钱，多少时间才能还清？如果要10年还清，每月需还多少？分析：记第k个月末他欠银行的钱为x（k），月利率为r，且a=1+r，b为每月还的钱。
则第k+1个月末欠银行的钱为x(k+1)=a*x(k)+b，a=1+r，b=-1000，k=0，1，2…在r=0.005 及x0=100000 代入，用MA TLAB 计算得结果。
差分方程习题1、对下面的差分方程，求出它们的1X 、2X 、3X 、4X 的值：(a) 1,301=+=+X X X n n (b) 2,35.001=+=+X X X n n (c) 1,02/121=+=+X X X X n n n(d)1),sin(01==+X X X n n （采用弧度）2、 对下面的差分方程进行分类（填入表内）3、 若 47,23,11,5,243210=====X X X X X ，根据以上数据，写出用1+n X 和n X 表示的差分方程。
4、 若每年有%X 的现有的汽车报废，而且每年新购人N 辆汽车，建立反映n 年后汽车总数n C 的差分方程。
5、 一轿车油耗指标是每加仑30英里，建立一个以n 为英里，n X 为汽油加仑数的差分方程。
6、 某种植物第一天长高3cm ，之后每天长的高度是前一天的1/2，建立一个描述n天后植物高度n B 的差分方程。
7、 设某种昆虫在第n 个月的数量n I 与它两个月前成虫产的卵数和孵化出的幼虫第一月的成活率有关，做出求解昆虫在第n 月时数量的差分方程。
8、 某种树10年后可成材，若n P 表示第n 年时植入的树数，n M 表示第n 年时已成材的树数。
做出与n P ，n M 有关的差分方程，如果C 是每年要砍伐的树数，模型应做何修正。
9、 若生产增长速率每年是4%，n P 表示第n 年时的产量，做出描述产量模型的差分方程。
若1990年时的产量是1千万吨，请估计：（a ）什么时候产量可达1千4百万吨；（b ）什么时候其产量低于6百万吨。
10、 某机器的折旧率是每年5%，建立一个描述其折旧值n V 的差分方程，如果新购入时花了10000元，当它的折旧值仅为3000元时，机器将报废，计算：（a ）5年后机器的价值；（b ）机器使用年限。
11、 某公司刚生产出一种新产品，计划每月增产2000件，第一个月共生产了5000件，要求估测在哪一个月产量（1）将超过20000件；（2）将到达N 件。
第7章离散时间系统的Z域分析7.1 学习要求（1）深刻理解z变换的定义、收敛域及基本性质，会根据z变换的定义和性质求解一些常用序列的z变换，能求解z反变换，深刻理解z变换与拉普拉斯变换得关系；（2）正确理解z变换的应用条件；（3）能用z域分析分析系统，求离散系统的零状态响应、零输入响应、完全响应、单位样值响应；（4）深刻理解系统的单位样值响应与系统函数H(z)之间的关系，并能用系统函数H(z)求解频率响应函数，能用系统函数的分析系统的稳定性、因果性。
7.2 本章重点（1）z变换（定义、收敛域、性质、反变换、应用）；（2）z域分析（求解分析系统）；（3）系统的频率响应函数。
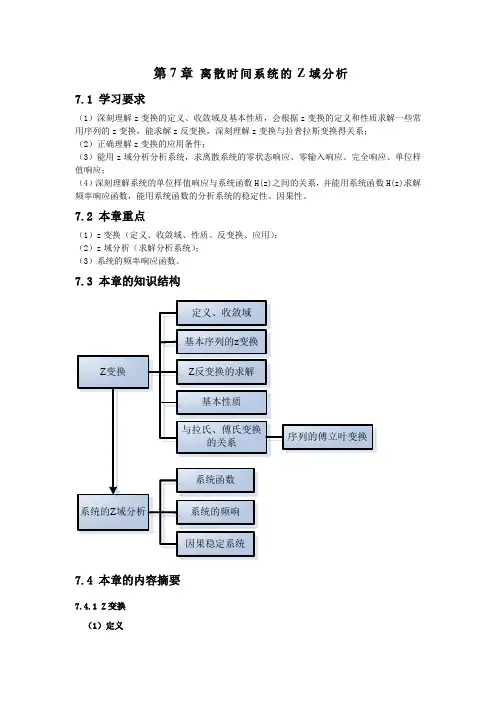
7.3 本章的知识结构7.4 本章的内容摘要7.4.1 Z变换（1）定义∑∞-∞=-=n nzn x z X )()( 表示为：)()]([z X n x Z =。
（2）收敛域 1.有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他 （1）当0,021>>n n 时，n 始终为正，收敛条件为0>z ； （2）当0,021<<n n 时，n 始终为负，收敛条件为∞<z ；（3）当0,021><n n 时，n 既取正值，又取负值，收敛条件为∞<<z 0。
2.右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩ （1）当01>n 时，n 始终为正，由阿贝尔定理可知，其收敛域为1x R z >，1x R 为最小收敛半径；（2）当01<n 时，)(z X 分解为两项级数的和，第一项为有限长序列，其收敛域为∞<z ；第二项为z 的负幂次级数，由阿贝尔定理可知，其收敛域为1x R z >；取其交集得到该右边序列的收敛域为∞<<z R x 1。
3．左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他（1）当02<n ，n 始终为负，收敛域为2x R z <，2x R 为最大收敛半径； （2）当02>n ，)(z X 可分解为两项级数的和，第一项为z 的正幂次级数，根据阿贝尔定理,其收敛域为2x R z <，2x R 为最大收敛半径；第二项为有限长序列，其收敛域为0>z ；取其交集，该左边序列的收敛域为20x R z <<。
