当前位置：文档之家 › 差分方程模型习题+答案

差分方程模型习题+答案

  • 格式：doc
  • 大小：176.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

微分差分方程习题答案(上大)

微分差分方程习题答案(上大)

第七章 微分方程与差分方程习题7－1（A ）1．一阶)1( 二阶)2( 一阶)3( 2. (1) 不是 (2) 是 (3) 是 (4) 是3．25)1(22=-x y x xe y 2)2(= x y c o s)3(-= 4．2)1(x y = 02)2(=+'x y y习题7－1（B ）1．1)1()1(22=+'y y 02)2(=-'+''xy y y x 2．)()1(2为比例系数k TPk dT dP = )()2(21为比例系数k v k t k dtdvm-= 习题7－2（A ）1．xC e y =)1( C x x y ++=325121)2( )1(ln 1)3(x a a C y --+=C x y =+-1010)4( C x y +=a r c s i n a r c s in )5( C x y +--=2212)6( 34121)21()7(x y C -=-C y x =t a n t a n)8( 3)1(t a n )9(-=x e C y C e e y x =-+)1()1()10(2．)1(21)1(2+=xy e e 0c o s 2c o s )2(=-y x 2tan )3(x ey = )1(ln 21)1(ln 2)4(2e e y x +-++=6.3=xy231.4x y =习题7－2（B ）)(10,64.90305.0.123s h t 水流完所需时间约为+-=)/(3.26972500.2s cm v ≈=t e R R 000433.00.3-=t et v 52ln 6)(.4-=t k mt k me v e g kmv --+-=0)1(.51)1(.6--=m axb y31.7xe C y x-=习题7－3（A ）1．1)1(+=x C e x y 222)2(Cx x y y =-+)(ln )3(222Cx x y =2)ln()4(x C x y = )0()5(>=x e x y x C xy sh C x 32)6(= 2．x xyln sin)1(= 2)2(22=++y x y3． C xy =4．C y x y =++22习题7－3（B ）1．331)1(yCy x =- C ye x x y=+2)2( 223)3(x y y -= 1)4(22=++yx y x2*． Cy x y x C x y x y Cx yx y C x y x y =--++=-++-=-+-+=-+--)2(ln 23)4()1()1()3(12arctan])1(4ln[)2()32()34()1(52222 习题7－4（A ）1．)()1(C x e y x +=- )()2(s i n C x e y x+=-)(1)3(2x x e Ce xy +=x x C y 2c o s 2c o s)4(-= 1sin )5(2-+=x Cx y )2()2()6(3-+-=x C x y 2．xxy cos 1)1(--=π xxy cos )2(=15sin )3(cos =+x e x y )4(32)4(3θρ--=e )1(2)5(1132--=xe x y3．)1(2--=x e y x 4．,)1()()2(,)()1(kt e a a t y a y k dtdy--+=--= 量的相对忘记速率。

第八章差分方程模型

第八章差分方程模型

第八章 差分方程模型差分方程是解决离散时间问题的常用的数学方法，本章介绍几个用差分方程建立的实际问题的数学模型。

8.1个人住房抵押贷款随着经济的发展,金融问题正越来越多地进入普通市民的生活，贷款、保险、养老金和信用卡等都涉及金融问题，个人住房抵押贷款是其中最重要的一项。

1998年12月,中国人民银行公布了新的存、贷款利率水平,其中贷款利率如下表所列:表8.1 中国人民银行贷款利率表贷款期限 半年 一年 三年 五年 五年以上 利率﹪ 6.126.396.667.207.56当贷款期处于表中所列相邻年限之间时利率为对应相邻两数中较大者。

其后,上海商业银行对个人住房商业性贷款利率作出相应调整。

表8.2和表8.3分别列出了上海市个人住房商业抵押贷款年利率和商业抵押贷款(万元)还款额的部分数据(仅列出了五年)。

表8.2 上海市商业银行住房抵押贷款利率表贷款期限 一年 二年 三年 四年 五年 利率﹪ 6.12 6.2256.3906.5256.660表8.3 上海市商业银行住房抵押贷款分期付款表贷款期限 一年 二年 三年 四年 五年 月还款（元） 到期一次还清 本息总和（元） 10612.00 444.36 10664.54305.99 11015.63237.26 11388.71196.41 11784.71一个自然的问题是,表8.2和表8.3是如何依据中央人民银行公布的存、贷款利率水平制定的？我们以商业贷款10000元为例,一年期贷款的年利率为 6.12﹪,到期一次还本付息总计10612.00元,这很容易理解。

然而二年期贷款的年利率为6.225﹪,月还款数444.36元为本息和的二十四分之一,这后两个数字究竟是怎样产生的？是根据本息总额算出月还款额，还是恰好相反？让我们稍微仔细一些来进行分析。

由于贷款是逐月归还的,就有必要考察每个月欠款余额的情况。

设贷款后第k 个月时欠款余额为A k 元，月还款m 元,则由A k 变化到A k +1,除了还款额外,还有什么因素呢？无疑就是利息。

差分方程与自回归模型练习解答

差分方程与自回归模型练习解答

差分方程与自回归模型练习解答1差分方程为x t+i =1.5x t -500 (单位：百万；此时，免疫系统仍起作用，但其杀死的病毒相对 于打针吃药被忽略了)。

利用方程平衡点，讨论多久去治病毒可以控制住(此时病毒数做新 的初始值)，多久去到医院也没用来解答。

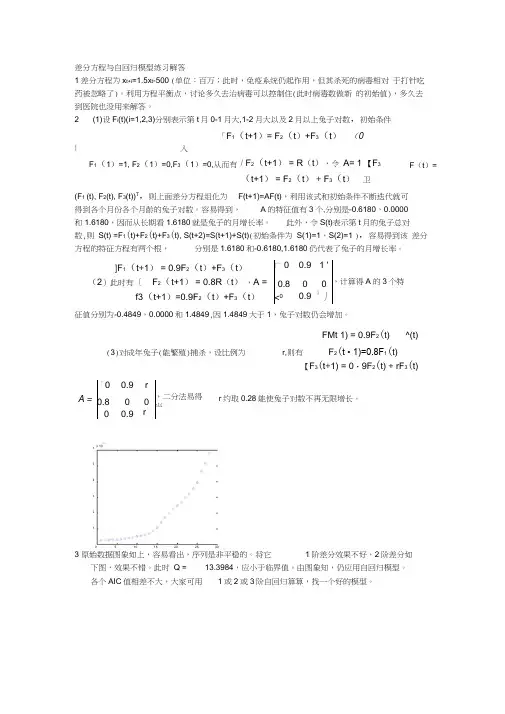
2(1)设F i (t)(i=1,2,3)分别表示第t 月0-1月大,1-2月大以及2月以上兔子对数，初始条件「F 1（t+1）= F 2（t ）+F 3（t ） （0I入/ F 2（t+1） = R （t ），令 A= 1 【F 3（t+1） = F 2（t ） + F 3（t ）卫(F 1 (t), F 2(t), F 3(t))T ，则上面差分方程组化为 F(t+1)=AF(t)，利用该式和初始条件不断迭代就可得到各个月份各个月龄的兔子对数。

容易得到，A 的特征值有3个,分别是-0.6180，0.0000和1.6180，因而从长期看1.6180就是兔子的月增长率。

此外，令S(t)表示第t 月的兔子总对数,则 S(t) =F 1(t)+F 2(t)+F 3(t), S(t+2)=S(t+1)+S(t)(初始条件为 S(1)=1，S(2)=1 )，容易得到该 差分方程的特征方程有两个根，分别是1.6180和-0.6180,1.6180仍代表了兔子的月增长率。

]F 1（t +1） = 0.9F 2（t ）+F 3（t ）广0 0.9 1 '（2）此时有｛ F 2（t+1） = 0.8R （t ） ，A = 0.8 0 0 ，计算得A 的3个特f3（t+1）=0.9F 2（t ）+F 3（t ） <0 0.9 1丿征值分别为-0.4849，0.0000和1.4849,因1.4849大于1，兔子对数仍会增加。

FMt 1) = 0.9F 2(t)^(t)(3)对成年兔子(能繁殖)捕杀，设比例为r,则有F 2(t • 1)=0.8F 1(t)【F 3(t +1) = 0・9F 2(t) + rF 3(t)3 原始数据图象如上，容易看出，序列是非平稳的。

数学模型(差分方程)

数学模型(差分方程)

定义为
X ( z ) Z [ x(k )] x(k ) z k
k 0 k

其中z是复变量，因此级数 x(k ) z 的收敛域为某个圆的外部。
k 0
X ( z)
的Z反变换记作 x(k ) Z 1[ X ( z)]
(k )

1.几个常用离散函数的变换
一部分为当月新生的，而由题设知当月新生的兔子对数等于上上月
兔子对数，所以
h(n) h(n 1) h(n 2), n 3 h(1) h(2) 1
一、常系数线性齐次差分方程的求解方法-解析法 形如
h(n) a1h(n 1) a2h(n 2) ak h(n k ) 0 (n k , k 1,) (1)
h(n) h(n 1) 3h(n 2) 5h(n 3) 2h(n 4) 0 ( n 4,5, )
的特解 . 解：该差分方程对应的特征方程为
x 4 x3 3x 2 5 x 2 0
x 其根为：1 x2 x3 1, x4 2 ，所以
令l k N
特别地 Z[ x(k 1)] z[ X ( z) X (0)] 证 ： Z[ x(k N )] x(k N ) z
k 0 N
l l 0
k

x(l ) z
l N
l N
z
N
=z [ x(l ) z x(l ) z l ] z N [ X ( z ) x(k ) z k ]
差分方程的通解为：
t
mi
重根，则该
h(n) h1 (n) h2 (n) ht (n) hi (n)

11 第十一章 差分方程 习题详解

11 第十一章 差分方程 习题详解

λ − 2 = 0，
特征根为 λ = 2 ．故所求通解为
2
y x = C 2 x ( C 为任意常数).
(2) 方程对应的齐次方程 y x +1 − y x = 0 的特征方程为
λ −1 = 0 ，
其特征根为 λ = 1 .所以齐次方程的通解为 Yx = C ( C 为任意常数). 由于 1 是特征方程的根，所以方程的特解具有形式 y x = bx ，代入方程，并比较两端同
=1
所以，函数 y t = C1 + C 2 2 − t 是差分方程的通解．
t
(2) 由初始条件 y0 = 0 ， y1 = 3 ，得
⎧C1 + C2 = 0 ， ⎨ ⎩C1 + 2C2 − 1 = 3
解之得， C1 = −4 ， C2 = 4 ．故所求特解为 y t = −4 + 2
t+2
−t ．
解
(1) 方程 Δy x − 3 y x = 0 改写为 y x +1 − 4 y x = 0 ，它的特征方程为
λ − 4 = 0，
特征根为 λ = 4 ．故所求通解为
yx = C 4 x ( C 为任意常数).
由 y 0 = 1 ，得 C = 1 ，故原方程满足初始条件的特解为
yx = 4 x .
x
4．已知 y x = e 是方程 y x +1 + ay x −1 = 2e 的一个解，求 a ． 解 因为 y x = e 是方程 y x +1 + ay x −1 = 2e 的一个解，所以 e
x x
x +1
+ ae x −1 = 2e x ，
即 e + a = 2e ，故 a = e( 2 − e) ．

差分方程的动态模型

差分方程的动态模型

差分方程的动态模型当然，请看以下试题：1. 根据差分方程的动态模型，动态模型是指：A. 只包含差分方程的模型B. 随时间变化的数学模型C. 静态的数学模型D. 不包含时间因素的模型2. 差分方程描述的是：_________________ (填空题)3. 差分方程的解法可以通过什么方法求得？请简要描述：_________________ (填空题)4. 差分方程中的“差分”指的是什么？请简要解释：_________________ (填空题)5.在动态模型中，如果一个系统的状态随时间变化，这种变化通常由哪种数学工具描述？ _________________ (填空题)6. 下列哪个不是差分方程的应用领域？A. 经济学B. 物理学C. 生物学D. 静态学7. 差分方程的初始条件是指什么？ _________________ (填空题)8. 差分方程的解可以分为哪两种类型？请简要描述：_________________ (填空题)9. 差分方程在数学建模中的作用是什么？_________________ (填空题)10. 差分方程的核心概念是什么？ _________________ (填空题)11.差分方程模型中，如何确定系统的稳定性？请简要描述：_________________ (填空题)12.差分方程中的“差分”操作类似于微分方程中的哪个操作？_________________ (填空题)13. 在差分方程中，离散变量的意义是什么？_________________ (填空题)14.差分方程与微分方程相比，在描述哪类问题上更加适用？_________________ (填空题)15. 差分方程的阶数指的是什么？请简要解释：_________________ (填空题)16.差分方程模型中，时间步长的选择对模型精度有何影响？请简要描述： _________________ (填空题)17. 差分方程中的递推关系是指什么？ _________________ (填空题)18. 差分方程的数学形式是什么？ _________________ (填空题)19. 差分方程的数学表达中通常包含哪些元素？_________________ (填空题)20.差分方程模型在实际应用中的一个具体例子是什么？请简要描述： _________________ (填空题)这些试题涵盖了差分方程的基本概念、应用和解法，希望能够满足你的需求。

差分方程练习题

差分方程练习题
t
1 5 (4) y t 1 y t . 2 2 7. 求下列差分方程在给定初始条件下的特解：
(1) yt +1- yt =10，且 y0 =3； (2) yt +1-2 yt =2t ，且 y0 =2. 8. 求下列二阶常系数线性齐次差分方程的通解或在给定初始条件下的特解：
(3) yt ln(t 1) ln t ,
2 yt (yt ) ln(t 1) ln t ln(t 2) 2ln(t 1) ln t
(4) yt t 1 3t 1 t 2 3t 3t 2t 2 6t 3 ,
yt 3 1 0 t .

t
(2) 原 方 程 的 通 解 为 yt C 2t t 2t 1 又 有 初 始 条 件 y0 =2 ， 可 知 C 2 , 故 特 解 为
yt 2t 1 t 2t 1 .
8. （1） yt C1 3t C2 2 .
t
（1） yt 2 yt 1 6 yt 0 （2） yt 2 6 yt 1 9 yt 0 （3） yt 2 13 yt 1 12 yt 0 ； y0 1, y1 6 9. 求下列二阶常系数线性非齐次差分方程的通解： （1）yx +2 3yx +1 + 2yx = 2x （2） yt 2 yt 1 6 yt 6 （3） yt 2 6 yt 1 9 yt 8 答案 1. 解：(1) yt ［3 t 1 t 1 ］ 3t 2 t 3 3t 2 +3t 2 ,
yt 9 6t 3t 2 C 2t .
* *
3 5 ( )t ，解得 A . (4) 由 a 1 ，k 1，b 5 ，令原方程有一个特解为 y*t A· 5 2 2 2

差分方程例题

差分方程例题
∞
∑ (3) f3(k) ∗ f4 (k) = f3(i) f4 (k − i) i = −∞
k < 0 时： f (k) = 0 k = 1时： f (k) = −1 k = 2 时： f (k) = 2 k = 3 时： f (k) = −2 k = 4 时： f (k) = −1 k = 5 时： f (k) = −1 k > 5 时： f (k) = 0
f23(k) = {...0,3,5, 6, 6, 6,3,1, 0...}
f13(k) = {...0, 0,3,8,8, 4,1, 0, 0...} f (k) = {...0,3, 2, −2, −图所示系统，若激励 f (k) = (1)k ε (k) ，求系统的零状态响应。 2
k > 3 时： f (k) = 0
6
∞
∑ (2) f2 (k) ∗ f3(k) = f2 (i) f3(k − i) i = −∞
k = −3 时： f (k) = 0 k = −2 时： f (k) = 3 k = −1 时： f (k) = 5 k = 0 时： f (k) = 6 k = 1, 2 时： f (k) = 6 k = 3 时： f (k) = 3 k = 4 时： f (k) = 1 k > 4 时： f (k) = 0
y(k)
f(k) + ∑
D
D
+
3/4
1/8
解：系统的差分方程为：
y(k) = f (k) + 3 y(k −1) − 1 y(k − 2)
(4) h(k) + 4h(k − 2) = δ (k)
λ2
+
4
=
0

差分方程模型

差分方程模型

设特解为 an D 代入 D 0.5D 0.1 得 D 0.2 ， 于是所求通解 an c(0.5) n 0.2 例3 (养老金) 解: 齐次特征方程 设特解 an D
an1 1.01an 1000
1.01 0,
* an c(1.01) n.
代入原方程得 D 100000
例 4 求非齐次差分方程
* 对应齐次方程的通解为 an c1 2n c2 n 2n
的通解
f (n) 2 中, 2 是2 重根, 设特解为
n
an A n 2 2 n
n 2 n1
代入
得 A 1 2 方法2 (化齐) :
故通解为 an c1 2 c2 n 2 n 2
Fn Fn 1 Fn 2 F1 F2 1
解：差分方程的特征方程为 x 2 x 1 0 特征根
x1
n
1 5 1 5 , x2 2 2
n
1 5 1 5 Fn c1 c2 2 2
n
2(an1 4an2 4an3 ) 2 2n1 相减得 an 6an1 12an2 8an3 0 特征方程 3 62 12 8 0 特征根 2 为三重根, 通解为：
an 4an1 4an2 2n
an c1 2n c2 n 2n c3n 2 2n
x k b1 x k 1 b2 x k 2 bk 0
称为差分方程的特征方程，其根称为特征根。 定理1（单根）若特征方程恰有k个相异的特 x1 , x2 ,, x 征根 ， k 则差分方程的通解为
an c x c x ck x

习题详解-第10章 微分方程与差分方程初步

习题详解-第10章 微分方程与差分方程初步

两端分别积分：
2 y 2x +ln2 C1 ,即 2x +2 y C 0( C ln 2 C1 )
这就是方程通解 . (3)这是可分离变量方程，分离变量得
cos y dy cos x dx sin y sin x
两端分别积分：
ln sin y ln sin x ln C , 即 sin y Cesinx
是解，又因为含有两个任意常数 C1,C2 ，且方程是二阶的，故是通解.
4.
已知函数
x=C1coskt+C2sinkt(k≠0)是微分方程
d2x dt 2
k2x
0 的通解,求满足初始条件
x| t0 2 x| t0 0
的特解. 解 ： 上 题 可 知 是 微 分 方 程 通 解 ， 且 x(t) C1k sin kt C2k cos kt, 代 入 初 值 条 件 x |t 0 2, x |t0 0 ，得 C1 2,C2 0 ，所以特解为 x 2coskt(k 0).
x dx
dx
u 1 du dx u
两端分别积分：
u ln u x C 即 y ln y x C xx
这就是方程通解 .
(6)这是齐次方程，化简得
dy
1
y x
dx 1 y
x
令 u y , 则 dy u du , 代入原方程并整理
x dx
dx
u 1 du dx ，两端分别积分： 1 ln 1 2u u2 x 1 C
(3)
y
x
y y2
，
y(2)
1；
(4) y y x y5 ， y(0) 1 .
解 (1)这是一个齐次线性方程,整理得
dy dx

第三章差分方程模型

第三章差分方程模型
例 每月存入3000元，存期５年（年利率3.5%） 累计存入金额180,000元
零存整取
计算器
到期本息总额196,012.50元
勤俭节约、科学理财
单利和复利
按单利计算的业务——零存整取
a~每月存入金额, r ~月利率, n ~ 存期(月) xk ~存入k个月后的本息 x1=a+ar xk= xk-1+a+akr, k＝2,3,…, n xn= na+ar(1+2+…+n)
xk 2 a1xk 1 a2 xk b, x0 , x1已知，k 0,1,2,
• 由x0, x1按照方程递推地计算x2, x3,…
•
k k 求解公式 xk c11 c22
b , k 0,1,2, 1 a1 a2
1, 2～特征根
2 a1 a2 0 ~ 特征方程
=1/8000(kg/kcal)
~代谢系数(因人而异).
w(k 1) w(k ) c(k ) w(k ), k 1,2,
由和吸收热量 c(k)决定体重w(k)的变化规律.
减肥计划的提出
某人身高1.70m, 体重100kg, BMI高达34.6. 目前每周 吸收20000kcal热量,体重长期未变.
建立等额本息还款方式的数学模型, 并作数值计算．
等额本息还款模型 x0 ~贷款总额 r ~月利率 n ~贷款期限(月)
xk ~第k月还款后尚欠金额
a~每月还款金额
本月欠额=上月欠额的本息还款金额 xk= xk-1(1+r)a, k＝1,2,…, n
k=n递推至k=１
n ( 1 r ) 1 n n n1 x ( 1 r ) a xn= x0(1+r) a[1+(1+r)+…+(1+r) ] 0 r

微积分第2版-朱文莉第10章 微分方程与差分方程习题详解(1-3节)

微积分第2版-朱文莉第10章 微分方程与差分方程习题详解(1-3节)

微积分第2版-朱文莉第10章微分方程与差分方程习题详解(1-3节)题10.1(A)1.指出下列微分方程的阶数：1) x(y')-2yy'+x=；2) y^2(4)+10y''-12y'+5y=sin2x；3) (7x-6y)dx+(x+y)dy=S；4) 2d^2S/dt^2+S=0.解：(1) 1阶；(2) 4阶；(3) 1阶；(4) 2阶。

2.判断下列各题中的函数是否为所给微分方程的解？若是解，它是通解还是特解？1) x(dy/dx)=-2y，y=Cx^-2（C为任意常数）；2) 2x(y'')-2y'+y=0，y=xe；3) y''-2/(y'+y)=0，y=C1x+C2/x^2（C1，C2为任意常数）；4) xdx+ydy=R，x+y=const（R为任意常数）。

解：(1) 通解；(2) 否；(3) 通解；(4) 通解。

3.验证：函数y=(C1+C2x)e^-x（C1，C2为任意常数）是方程y''+2y'+y=的通解，并求满足初始条件y(0)=4，y'(0)=-2的特解。

解：由已知得y=C1e^-x+C2xe^-x，y'=C2e^-x-C1e^-x-C2xe^-x。

将y代入方程得(C1-2C2)e^-x=0，因为e^-x不为0，所以C1=2C2.所以通解为y=(C1+C2x)e^-x=(2C2+2C2x)e^-x=(2+2x)e^-x。

将初始条件代入得C1=4，C2=2，所以特解为y=(4+2x)e^-x。

4.已知曲线上任一点(x,y)处的切线斜率等于该点的横坐标与纵坐标的乘积，求该曲线所满足的微分方程。

解：根据题意，设曲线为y=f(x)，则斜率为f'(x)，根据题意得f'(x)=xf(x)，即y'=xy，所以微分方程为dy/dx=xy。

数学建模习题及答案课后习题

数学建模习题及答案课后习题

数学建模习题及答案课后习题第⼀部分课后习题1.学校共1000名学⽣，235⼈住在A宿舍，333⼈住在B宿舍，432⼈住在C宿舍。

学⽣们要组织⼀个10⼈的委员会，试⽤下列办法分配各宿舍的委员数：（1）按⽐例分配取整数的名额后，剩下的名额按惯例分给⼩数部分较⼤者。

（2）节中的Q值⽅法。

（3）d’Hondt⽅法：将A，B，C各宿舍的⼈数⽤正整数n=1，2，3，…相除，其商数如下表：将所得商数从⼤到⼩取前10个（10为席位数），在数字下标以横线，表中A，B，C⾏有横线的数分别为2，3，5，这就是3个宿舍分配的席位。

你能解释这种⽅法的道理吗。

如果委员会从10⼈增⾄15⼈，⽤以上3种⽅法再分配名额。

将3种⽅法两次分配的结果列表⽐较。

（4）你能提出其他的⽅法吗。

⽤你的⽅法分配上⾯的名额。

2.在超市购物时你注意到⼤包装商品⽐⼩包装商品便宜这种现象了吗。

⽐如洁银⽛膏50g装的每⽀元，120g装的元，⼆者单位重量的价格⽐是：1。

试⽤⽐例⽅法构造模型解释这个现象。

（1）分析商品价格C与商品重量w的关系。

价格由⽣产成本、包装成本和其他成本等决定，这些成本中有的与重量w成正⽐，有的与表⾯积成正⽐，还有与w⽆关的因素。

（2）给出单位重量价格c与w的关系，画出它的简图，说明w越⼤c越⼩，但是随着w的增加c减少的程度变⼩。

解释实际意义是什么。

3.⼀垂钓俱乐部⿎励垂钓者将调上的鱼放⽣，打算按照放⽣的鱼的重量给予奖励，俱乐部只准备了⼀把软尺⽤于测量，请你设计按照测量的长度估计鱼的重量的⽅法。

假定鱼池中只有⼀种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼⾝的最⼤周长）：⾝长（cm）重量76548211627374821389652454（g）胸围（cm）先⽤机理分析建⽴模型，再⽤数据确定参数4.⽤宽w的布条缠绕直径d的圆形管道，要求布条不重叠，问布条与管道轴线的夹⾓应多⼤（如图）。

若知道管道长度，需⽤多长布条（可考虑两端的影响）。

如果管道是其他形状呢。

差分方程模型介绍

差分方程模型介绍
function x=zwfz(x0,n,b) c=10;a1=0.5;a2=0.25; p=a1*b1*c; q=a2*b*91-a1)*b*c; x(1)=x0; x(2)=p*x(1); for k=3:n x(k)=p*x(k-1)+q*x(k-2); end
结果分析：Xk= pXk-1 + qXk-2
∗ 以k=0时X0=M代入，递推n次可得n年后本息为
xn = (1 + r ) M
n
∗ 例2 污水处理厂每天可将处理池的污水浓度降低一个固 定比例q，问多长时间才能将污水浓度降低一半？ ∗ 记第k天的污水浓度为Ck,则第k+1天的污水浓度为 Ck+1=(1q)Ck, k=0,1,2,···· 从k=0开始递推n次得
模型及其求解
∗ 记一棵植物春季产种的平均数为C,种子能活过一个冬天的 (1岁种子)比例为b,活过一个冬天没有发芽又活过一个冬天 的（2岁种子）比例仍为b,1岁种子发芽率a1，2岁种子发芽 率a2。 ∗ 设C,a1,a2固定，b是变量，考察能一直繁殖的条件 ∗ 记第k年植物数量为Xk，显然Xk与Xk-1,Xk-2有关，由Xk-1决 定的部分是 a1bCXk-1,由Xk-2决定的部分是 a2b(1-a1)bCXk-2
• 用矩阵表示
x1 (k + 1) 0.6 0.2 0.1 x1 (k ) x2 (k + 1) = 0.3 0.7 0.3 x2 ( k ) x (k + 1) 0.1 0.1 0.6 x ( k ) 3 3
λ1,2 < 1, xk → 0(k → ∞)
λ 1, 2 > 1, x k → ∞ ( k → ∞ )

差分方程模型习题+答案

差分方程模型习题+答案

1. 一老人60岁时将养老金10万元存入基金会，月利率0.4%， 他每月取1000元作为生活费，建立差分方程计算他每岁末尚有多少钱？多少岁时将基金用完？如果想用到80岁，问60岁时应存入多少钱？分析：(1) 假设k 个月后尚有k A 元，每月取款b 元，月利率为 r ，根据题意，可每月取款，根据题意，建立如下的差分方程：1k k A aA b +=-，其中a = 1 + r (1)每岁末尚有多少钱,即用差分方程给出k A 的值。

(2) 多少岁时将基金用完，何时0k A =由（1）可得：01kkk a A A a br-=-若0n A =，01nnA rab a =-(3) 若想用到 80 岁，即 n ＝(80-60)*12=240 时，2400A =，24002401A ra b a=-利用 MA TLAB 编程序分析计算该差分方程模型，源程序如下： clear all close allclcx0=100000;n=150;b=1000;r=0.004; k=(0:n)';y1=dai(x0,n,r,b); round([k,y1'])function x=dai(x0,n,r,b) a=1+r; x=x0;for k=1:nx(k+1)=a*x(k)-b; end(2)用MA TLAB 计算：A0=250000*(1.004^240-1)/1.004^240思考与深入：(2) 结论：128个月即70岁8个月时将基金用完(3) A0 = 1.5409e+005结论：若想用到80岁，60岁时应存入15.409万元。

2. 某人从银行贷款购房，若他今年初贷款10万元，月利率0.5%，他每月还1000元。

建立差分方程计算他每年末欠银行多少钱，多少时间才能还清？如果要10年还清，每月需还多少？分析：记第k个月末他欠银行的钱为x（k），月利率为r，且a=1+r，b为每月还的钱。

则第k+1个月末欠银行的钱为x(k+1)=a*x(k)+b，a=1+r，b=-1000，k=0，1，2…在r=0.005 及x0=100000 代入，用MA TLAB 计算得结果。

差分方程习题

差分方程习题

差分方程习题1、对下面的差分方程，求出它们的1X 、2X 、3X 、4X 的值：(a) 1,301=+=+X X X n n (b) 2,35.001=+=+X X X n n (c) 1,02/121=+=+X X X X n n n(d)1),sin(01==+X X X n n （采用弧度）2、 对下面的差分方程进行分类（填入表内）3、 若 47,23,11,5,243210=====X X X X X ，根据以上数据，写出用1+n X 和n X 表示的差分方程。

4、 若每年有%X 的现有的汽车报废，而且每年新购人N 辆汽车，建立反映n 年后汽车总数n C 的差分方程。

5、 一轿车油耗指标是每加仑30英里，建立一个以n 为英里，n X 为汽油加仑数的差分方程。

6、 某种植物第一天长高3cm ，之后每天长的高度是前一天的1/2，建立一个描述n天后植物高度n B 的差分方程。

7、 设某种昆虫在第n 个月的数量n I 与它两个月前成虫产的卵数和孵化出的幼虫第一月的成活率有关，做出求解昆虫在第n 月时数量的差分方程。

8、 某种树10年后可成材，若n P 表示第n 年时植入的树数，n M 表示第n 年时已成材的树数。

做出与n P ，n M 有关的差分方程，如果C 是每年要砍伐的树数，模型应做何修正。

9、 若生产增长速率每年是4%，n P 表示第n 年时的产量，做出描述产量模型的差分方程。

若1990年时的产量是1千万吨，请估计：（a ）什么时候产量可达1千4百万吨；（b ）什么时候其产量低于6百万吨。

10、 某机器的折旧率是每年5%，建立一个描述其折旧值n V 的差分方程，如果新购入时花了10000元，当它的折旧值仅为3000元时，机器将报废，计算：（a ）5年后机器的价值；（b ）机器使用年限。

11、 某公司刚生产出一种新产品，计划每月增产2000件，第一个月共生产了5000件，要求估测在哪一个月产量（1）将超过20000件；（2）将到达N 件。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1. 一老人60岁时将养老金10万元存入基金会，月利率0.4%， 他每月取1000元作为生活费，建立差分方程计算他每岁末尚有多少钱？多少岁时将基金用完？如果想用到80岁，问60岁时应存入多少钱？分析：(1) 假设k 个月后尚有k A 元，每月取款b 元，月利率为 r ，根据题意，可每月取款，根据题意，建立如下的差分方程：1k k A aA b +=-，其中a = 1 + r (1)每岁末尚有多少钱,即用差分方程给出k A 的值。

(2) 多少岁时将基金用完，何时0k A =由（1）可得：01kkk a A A a br-=-若0n A =，01nnA rab a =-(3) 若想用到 80 岁，即 n ＝(80-60)*12=240 时，2400A =，24002401A ra b a=-利用 MA TLAB 编程序分析计算该差分方程模型，源程序如下： clear all close allclcx0=100000;n=150;b=1000;r=0.004; k=(0:n)';y1=dai(x0,n,r,b); round([k,y1'])function x=dai(x0,n,r,b) a=1+r; x=x0;for k=1:nx(k+1)=a*x(k)-b; end(2)用MA TLAB 计算：A0=250000*(1.004^240-1)/1.004^240思考与深入：(2) 结论：128个月即70岁8个月时将基金用完(3) A0 = 1.5409e+005结论：若想用到80岁，60岁时应存入15.409万元。

2. 某人从银行贷款购房，若他今年初贷款10万元，月利率0.5%，他每月还1000元。

建立差分方程计算他每年末欠银行多少钱，多少时间才能还清？如果要10年还清，每月需还多少？分析：记第k个月末他欠银行的钱为x（k），月利率为r，且a=1+r，b为每月还的钱。

则第k+1个月末欠银行的钱为x(k+1)=a*x(k)+b，a=1+r，b=-1000，k=0，1，2…在r=0.005 及x0=100000 代入，用MA TLAB 计算得结果。

编写M 文件如下:function x=exf11(x0,n,r,b)a=1+r;x=x0;for k=1:nx(k+1)=a*x(k)+b;endMA TLAB计算并作图:k=(1:140)';y=exf11(100000,140,0.0005,-1000);所以如果每月还1000元，则需要11年7个月还清。

如果要10年即n=120 还清，则模型为：r*x0*(1+r)^n/[1-(1+r)^n b=-r*x0*(1+r)^n/[1-(1+r)^n]用MA TLAB 计算如下：>> x0=100000;>> r=0.005;>> n=120;>> b=-r*x0*(1+r)^n/[1-(1+r)^n]b= 1.1102e+003所以如果要10年还清，则每年返还1110.2元。

3. 在某种环境下猫头鹰的主要食物是田鼠，设田鼠的年平均增长率为1r，猫头鹰的存在引起的田鼠增长率的减少与猫头鹰的数量成正比，比例系数为1a；猫头鹰的年平均减少率为2r ；田鼠的存在引起的猫头鹰减少率的增加与田鼠的数量成正比，比例系数为2a 。

建立差分方程模型描述田鼠和猫头鹰共处时的数量变化规律，对以下情况作图给出50年的变化过程。

(1) 设12120.2,0.3,0.001,0.002,r r a a ====开始时有100只田鼠和50只猫头鹰。

（2）1212,,,r r a a 同上，开始时有100只田鼠和200只猫头鹰。

（3）适当改变参数12,a a （初始值同上） （4）求差分方程的平衡点，它们稳定吗？分析：记第k 代田鼠数量为k x ，第k 代猫头鹰数量为k y ，则可列出下列方程：111122()()k k k k k k k k x x r a y x y y r a x y ++=+-⎧⎨=+-+⎩运用matlab 计算，程序如下：function z=disanti(x0,y0,a1,a2,r1,r2) x=x0;y=y0; for k=1:49x(k+1)=x(k)+(r1-y(k)*a1)*x(k); y(k+1)=y(k)+(-r2+x(k)*a2)*y(k); endz=[x',y'];(1)z=disanti(100,50,0.001,0.002,0.2,0.3) plot(1:50,z(:,1)); hold on;plot(1:50,z(:,2),'r')(2)z=disanti(100,200,0.001,0.002,0.2,0.3) plot(1:50,z(:,1)); hold on;plot(1:50,z(:,2),'r')(3)当a1,a2分别取0.002,0.002时，得到如下图像：05101520253035404550可见，当a1,a2参数在一定范围内改变时，猫头鹰与田鼠数量在一定范围内震荡，且不灭绝。

(4)令1k k x x x +==；1k k y y y +== 解方程得到如下结果： x=150y=200经matlab 验证如下：z=disanti(150,200,0.001,0.002,0.2,0.3) plot(1:50,z(:,1)); hold on;plot(1:50,z(:,2),'r')由此可知：平衡点为：x=150 y=2004. 研究将鹿群放入草场后草和鹿两种群的相互作用。

草的生长遵从Logistic 规律，年固有增长率0.8，最大密度为3000（密度单位），在草最茂盛时每只鹿每年可吃掉1.6（密度单位）的草。

若没有草，鹿群的年死亡率高达0.9，而草的存在可使鹿的死亡得以补偿，在草最茂盛时补偿率为1.5。

作一些简化假设，用差分方程模型描述草和鹿两种群数量的变化过程，就以下情况进行讨论：（1）比较将100只鹿放入密度为1000和密度为3000的草场两种情况。

（2）适当改变参数，观察变化趋势。

模型假设：1．草独立生存，独立生存规律遵从Logistic 规律； 2．草场上除了鹿以外，没有其他以草为食的生物；3．鹿无法独立生存。

没有草的情况下，鹿的年死亡率一定； 4．假定草对鹿的补偿率是草场密度的线性函数；5．每只鹿每年的食草能力是草场密度的线性函数。

记草的固有增长率为r ，草的最大密度为N ，鹿独立生存时的年死亡率为d ，草最茂盛时鹿的食草能力为a ，草对鹿的年补偿作用为b ；第k ＋1年草的密度为 1k x +，鹿的数量为1k y +，第k 年草的密度为k x ，鹿的数量为k y 。

草独立生存时，按照Logistic 规律增长，则此时草的增长差分模型为1(1)k k k k x x x r x N+-=-，但是由于鹿对草的捕食作用，草的数量会减少，则满足如下方程：1(1), (0,1,2,)k k kk k k x ax y x x r x k N N+-=--= （1）鹿离开草无法独立生存，因此鹿独立生存时的模型为1k k k y y dy +-=-，但是草的存在会使得鹿的死亡率得到补偿，则满足如下差分方程：1(), (0,1,2,)k k k k bx y y d y k N+-=-+= （2）另外，记初始状态鹿的数量为0y ，草场密度初值为0x ，各个参数值为：，，，，利用MATLAB 编程序分析计算该差分方程模型，源程序如下：%定义函数diwuti ，实现diwuti-Logistic 综合模型的计算，计算结果返回种群量 function B =disiti(x0,y0,r,N,b,a,d,n) % 描述diwuti-Logistic 综合模型的函数 x(1) = x0; % 草场密度赋初值 y(1) = y0; % 鹿群数量赋初值 for k = 1 : n;x(k+1) = x(k) + r*(1-x(k)/N)*x(k) - a*x(k)*y(k)/N; y(k+1) = y(k) + (-d + b*x(k)/N)*y(k); endB = [x;y];%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear allC1 =disiti (1000,100,0.8,3000,1.5,1.6,0.9,50); C2 = disiti(3000,100,0.8,3000,1.5,1.6,0.9,50); k = 0 : 50;plot(k,C1(1,:),'b',k,C1(2,:),'b',k,C2(1,:),'r',k,C2(2,:),'r') axis([0 50 0 3000]);xlabel('时间/年')ylabel('种群量/草场：单位密度，鹿：头') title('图1.草和鹿两种群数量变化对比曲线') gtext('x0=1000') gtext('x0=3000') gtext('草场密度') gtext('鹿群数量')比较将100只鹿放入密度为1000和密度为3000的草场两种情况（绘制曲如图1所示）：由图中可以看到，蓝色曲线代表草场密度的初始值为1000时，两种群变化情况；而红色曲线则代表草场密度的初始值为3000时，两种群的变化情况。

观察两种情况下曲线的演变情况，可以发现大约40-50年左右时间后，两种群的数量将达到稳定。

使用MatLab 计算可以得到，当(,)(1800,600)k k k y y →∞=，即两种群数量的平衡点为（1800，600）。

为进一步验证此结论，下面通过改变相关参数，研究两种群变化情况，找到影响平衡点的因素：（1）改变草场密度初始值；从图2中可以看到，改变草场的初始密度不会对两种群数量的平衡点造成影响。

（2）改变鹿的数量初值由图2可以看到，鹿初始的数量的改变在理论上也不会改变最终种群数量的平衡值。

但是，我们可以看到，y0=2000的那条曲线（紫色曲线），在5－15区间内降低到了非常小的值，这显然是不符合鹿的现实繁殖规律的，因为鹿的种群可持续繁殖的最小数量是存在域值的。

当种群数量低于这个值时，在实际情况下，鹿的种群就要灭绝。

同样道理，草场的密度也存在一个最小量的域值，低于这个阈值，草也将灭绝。