1-第二章第一节容器壳体的应力分析
- 格式:ppt
- 大小:9.78 MB
- 文档页数:55

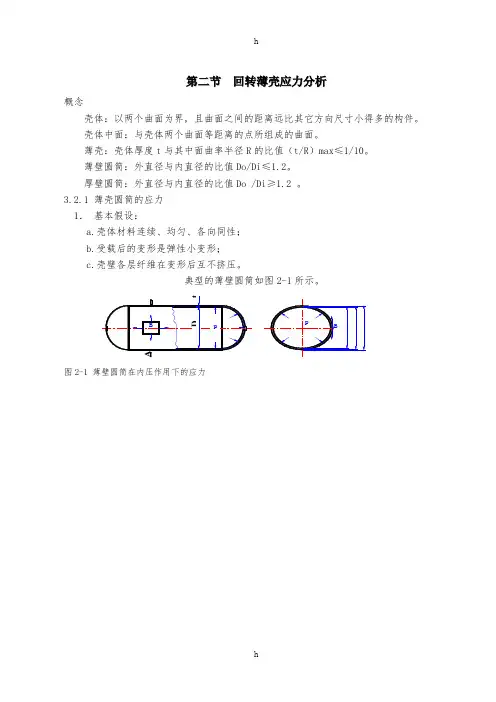
第二节回转薄壳应力分析概念壳体:以两个曲面为界,且曲面之间的距离远比其它方向尺寸小得多的构件。
壳体中面:与壳体两个曲面等距离的点所组成的曲面。
薄壳:壳体厚度t与其中面曲率半径R的比值(t/R)max≤1/10。
薄壁圆筒:外直径与内直径的比值Do/Di≤1.2。
厚壁圆筒:外直径与内直径的比值Do /Di≥1.2 。
3.2.1 薄壳圆筒的应力1.基本假设:a.壳体材料连续、均匀、各向同性;b.受载后的变形是弹性小变形;c.壳壁各层纤维在变形后互不挤压。
图2-12.B 点受力分析:内压P ( B 点):轴向:经向应力或轴向应力σφ圆周的切线方向:周向应力或环向应力σθ 壁厚方向:径向应力σr三向应力状态→(σθ 、σφ >>σr )→二向应力状态因而薄壳圆筒B 点受力简化成二向应力σφ和σθ(见图2-1) 3. 应力求解截面法图2-2 薄壁圆筒在压力作用下的力平衡应力求解 (静定,图2-2)220442sin 222i pDD p Dt tpD pR d t tϕϕπθθθϕππσσαασσσσ=====⎰轴向平衡得 圆周平衡 得 解得 3.2.2 回转薄壳的无力矩理论一、回转薄壳的几何要素:回转薄壳:中面是由一条平面曲线或直线绕同平面内的轴线回转而成。
母线:绕轴线(回转轴)回转形成中面的平面曲线,如OA极点:中面与回转轴的交点。
经线平面:通过回转轴的平面。
经线:经线平面与中面的交线,即OA'平行圆:垂直于回转轴的平面与中面的交线称为平行圆。
中面法线:过中面上的点且垂直于中面的直线,法线必与回转轴相交。
第一主曲率半径R1:经线上点的曲率半径。
第二主曲率半径R2:垂直于经线的平面与中面交线上点的曲率半径(K1B )等于考察点B到该点法线与回转轴交点K2之间长度(K2B)平行圆半径r:平行圆半径。
图2-3 回转薄壳的几何要素同一点的第一与第二主曲率半径都在该点的法线上。
曲率半径的符号判别:曲率半径指向回转轴时,其值为正,反之为负。


压力容器应力分析报告引言压力容器是一种用于储存或者输送气体、液体等介质的设备。
由于容器内的介质压力较高,容器本身需要能够承受这种压力而不发生破裂。
因此,对压力容器进行应力分析是非常重要的,它可以帮助我们判断容器的安全性并提供设计和改进的依据。
本报告旨在对压力容器进行应力分析,以评估其在工作条件下的应力分布情况,并根据分析结果提出相应的建议和改进措施。
1. 压力容器的工作原理和结构在进行应力分析之前,我们首先需要了解压力容器的工作原理和结构。
1.1 工作原理压力容器通过在容器内部创建高压环境来储存或者输送介质。
这种高压状态可以通过液体或气体的压力产生,也可以通过外部作用力施加于容器上。
容器的结构需要能够承受内部或外部压力的作用而不发生破裂。
1.2 结构压力容器通常由壳体、端盖、法兰、密封件等部分组成。
壳体是容器的主要结构部分,可以是圆柱形、球形或者其他形状。
端盖用于封闭壳体的两个端口,而法兰则用于连接不同部分的容器或其他设备。
密封件的选择和设计对于保证容器的密封性和安全性至关重要。
2. 压力容器应力分析方法在进行压力容器应力分析时,我们可以采用不同的方法和工具。
下面将介绍两种常用的应力分析方法。
2.1 解析方法解析方法是一种基于数学模型和理论计算的应力分析方法。
通过建立压力容器的几何模型和材料性质等参数,可以使用解析方程和公式计算容器内部和外部的应力分布情况。
这种方法适用于简单结构和边界条件的容器,具有计算简单、速度快的优点。
2.2 有限元方法有限元方法是一种基于数值计算的应力分析方法。
它将复杂的压力容器分割成有限个小单元,通过求解每个小单元的应力状态,再将它们组合起来得到整个容器的应力分布。
有限元方法可以考虑更多的几何和材料非线性,适用于复杂结构和边界条件的容器,具有更高的精度和可靠性。
3. 压力容器应力分析结果和讨论在进行压力容器应力分析后,我们得到了容器内部和外部的应力分布情况。
根据具体的分析方法和参数,以下是一些可能的结果和讨论。

压力容器壳体的稳定性分析一、引言压力容器壳体是蒸发器、换热器、反应器等化工设备中重要的组成部分,它承受来自内部介质的压力,同时还需要经受外部环境的力作用。
为了保证压力容器壳体能够在工作过程中保持稳定并安全地承受压力,必须对其进行稳定性分析。
本文将介绍压力容器壳体的稳定性分析方法和相关理论知识。
二、压力容器壳体的稳定性分析1. 应力状态在工作过程中,压力容器壳体承受来自内部介质的压力载荷,同时还需要经受外部环境荷载的作用,如风荷载等。
这些外部荷载会导致壳体上出现正应力和剪应力。
在确定压力容器壳体稳定性时需要先了解其压力状态。
在壳体内部,应力状态由压力载荷引起,应力分为径向应力、周向应力和轴向应力,其大小与压力载荷大小有关。
在壳体上,轻荷载下剪应力很小,只有正应力比较大,而在重载荷下,正应力和剪应力都较大。
2. 稳定性分析方法在确定壳体的稳定性时需要考虑其受力情况和力的分布情况,分析其受力状态并选择合适的分析方法。
稳定性分析方法有很多种,其中常用的有力学方法、能量方法、虚功原理和位移法等。
其中,力学方法主要是根据材料力学性质,通过应力计算得出壳体受到的外力大小,在此基础上确定其稳定性;能量方法是将壳体受到的外力转化成内能来研究稳定性;虚功原理是通过计算虚功来判断壳体的稳定性;位移法是通过计算变形、位移来判断壳体的稳定性。
在实际应用中,选取合适的分析方法需要考虑具体情况和要求。
3. 稳定性分析步骤(1)确定受力情况在进行压力容器壳体稳定性分析前,首先需要确定其所受外界荷载的大小和方向,同时还要考虑其内部介质压力的影响。
根据受力情况可以计算出壳体的应力状态。
(2)确定分析方法根据具体情况和要求选取合适的稳定性分析方法,应注意考虑分析的范围、精度和可靠性等因素。
必要时还需进行有限元分析。
(3)建立数学模型在使用分析方法进行计算前,需要建立数学模型来描述压力容器壳体的几何结构、物理性质以及受力情况等。
通常情况下,可以采取二维或三维模型。



《过程设备设计基础》教案2—压力容器应力分析课程名称:过程设备设计基础专业:过程装备与控制工程任课教师:第2章 压力容器应力分析§2-1 回转薄壳应力分析一、回转薄壳的概念薄壳:(t/R )≤0.1 R----中间面曲率半径 薄壁圆筒:(D 0/D i )max ≤1.1~1.2 二、薄壁圆筒的应力图2-1、图2-2 材料力学的“截面法”三、回转薄壳的无力矩理论1、回转薄壳的几何要素(1)回转曲面、回转壳体、中间面、壳体厚度 * 对于薄壳,可用中间面表示壳体的几何特性。
tpD td pR tpD Dt D p i 22sin 24422====⨯⎰θπθϕϕσσαασπσπ(2)母线、经线、法线、纬线、平行圆(3)第一曲率半径R1、第二曲率半径R2、平行圆半径r(4)周向坐标和经向坐标2、无力矩理论和有力矩理论(1)轴对称问题轴对称几何形状----回转壳体载荷----气压或液压应力和变形----对称于回转轴(2)无力矩理论和有力矩理论a、外力(载荷)----主要指沿壳体表面连续分布的、垂直于壳体表面的压力,如气压、液压等。
P Z= P Z(φ)b、内力薄膜内力----Nφ、Nθ(沿壳体厚度均匀分布)弯曲内力---- Qφ、Mφ、Mθ(沿壳体厚度非均匀分布)c、无力矩理论和有力矩理论有力矩理论(弯曲理论)----考虑上述全部内力无力矩理论(薄膜理论)----略去弯曲内力,只考虑薄膜内力●在壳体很薄,形状和载荷连续的情况下,弯曲应力和薄膜应力相比很小,可以忽略,即可采用无力矩理论。
●无力矩理论是一种近似理论,采用无力矩理论可是壳地应力分析大为简化,薄壁容器的应力分析和计算均以无力矩理论为基础。
在无力矩状态下,应力沿厚度均匀分布,壳体材料强度可以得到合理的利用,是最理想的应力状态。
(3)无力矩理论的基本方程a、无力矩理论的基本假设小位移假设----壳体受载后,壳体中各点的位移远小于壁厚。
考虑变形后的平衡状态时壳用变形前的尺寸代替变形后的尺寸直法线假设----变形前垂直于中面的直线变形后仍为直线,且垂直于变形后的中面。

百度文库- 让每个人平等地提升自我东北石油大学课程综合实践(二)课程过程设备设计题目典型局部应力学院机械科学与工程学院专业班级装备12-2班学生姓名李早东学生学号指导教师林玉娟2014年5月11日目录第一章局部应力 (1)1.局部应力的计算方法与概述 (1)WRC方法 (1)介质压力引起的应力计算 (3)强度评定 (3)欧盟的压力容器标准EN13445 (4)有限元法 (4)第二章补强分析 (5)2.降低局部应力的方法与措施 (5)直立容器支承式支座处的强度校核 (5)支座处封头的局部载荷 (5)支座处封头截面上的应力 (6)支座处封头的强度校核条件 (9)补强措施 (10)第三章结束语 (12)第一章局部应力1.局部应力的计算方法与概述压力容器除了承受介质压力载荷外,常常还要受到附件传来的其他外载荷。
通过支座、托架、吊耳等附件传来的载荷,主要是设备的自重及其内部物料等静重;通过接管传来的载荷主要是管道和管系反力、重量以及由于受热膨胀引起的推力和力矩。
这些载荷对壳体的影响虽仅限于附件与壳体连接处附近的局部区域,但常会产生较高的局部应力。
除外载荷产生的局部应力外,介质压力载荷还将在附件与壳体连接区产生另外一些局部应力,如局部薄膜应力、弯曲应力,以及截面尺寸突变的转角处的应力集中。
外载荷应力和介质压力载荷应力的联合作用将会使附件和壳体连接区域成为压力容器发生破坏的主要根源。
因此,计算外载荷作用下附件和壳体中的局部应力就显得十分重要,但是由于问题的非对称性,对局部应力作完整的理论计算过于复杂,对于实际设计往往不便于应用。
目前,对于压力容器壳体上由接管外载荷引起的局部应力的计算,主要有以Bijlaard理论为基础的两种方法:一是美国焊接研究协会(WRC)第107公报和有关补充规定WRC第297公报介绍的方法;二是英国压力容器设计标准BS550附录G建议的方法。
随着压力容器向高参数化发展和分析设计方法的广泛采用,要求进行局部应力计算和采用分析设计法进行强度评定的压力容器会越来越多,故本文在对WRC107方法理解基础上,对一高压反应器底封头上由接管载荷引起的局部应力作了详细计算,并按分析设计原理对接管和封头连接区的应力进行了强度评定,以便对工程中同类结构的局部应力计算、强度评定及压力容器分析设计方法的应用提供一定的参考。


化工容器(壳体、圆筒)应力分析BpBpADt第二节 回转薄壳应力分析概念壳体:以两个曲面为界,且曲面之间的距离远比其它方向尺寸小得多的构件。
壳体中面:与壳体两个曲面等距离的点所组成的曲面。
薄壳:壳体厚度t 与其中面曲率半径R 的比值(t/R )max ≤1/10。
薄壁圆筒:外直径与内直径的比值Do/Di ≤1.2。
厚壁圆筒:外直径与内直径的比值Do /Di ≥1.2 。
3.2.1 薄壳圆筒的应力 1. 基本假设:a.壳体材料连续、均匀、各向同性;b.受载后的变形是弹性小变形;c.壳壁各层纤维在变形后互不挤压。
图2.B 点受力分析:内压P ( B 点):轴向:经向应力或轴向应力σφ圆周的切线方向:周向应力或环向应力σθ 壁厚方向:径向应力σr三向应力状态→(σθ 、σφ >>σr )→二向应力状态因而薄壳圆筒B 点受力简化成二向应力σφ和σθ(见图2-1) 3. 应力求解截面法图2-2 薄壁圆筒在压力作用下的力平衡应力求解 (静定,图2-2)220442sin 222i pDD p Dt tpD pR d t tϕϕπθθθϕππσσαασσσσ=====⎰轴向平衡得 圆周平衡 得 解得 3.2.2 回转薄壳的无力矩理论σ ϕσ ϕσ θσ θppα(a)(b)yxD iθA'A x zyr a. b.R R K 1K 2平行圆经线ξrK 2K 1xO'O ϕϕR R B1212z一、回转薄壳的几何要素:回转薄壳:中面是由一条平面曲线或直线绕同平面内的轴线回转而成。
母 线:绕轴线(回转轴)回转形成中面的平面曲线,如OA 极 点:中面与回转轴的交点。
经线平面:通过回转轴的平面。
经 线:经线平面与中面的交线,即OA '平 行 圆:垂直于回转轴的平面与中面的交线称为平行圆。
中面法线:过中面上的点且垂直于中面的直线,法线必与回转轴相交。
第一主曲率半径R1:经线上点的曲率半径。