第五章 误差传播定律
- 格式:doc
- 大小:1.20 MB
- 文档页数:44




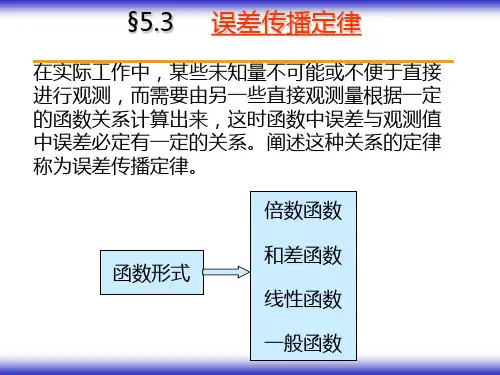
误差传播定律设有形如12(,,,,,)i n Z f x x x x = 的函数,其中12,,,n x x x 为可以直接观测的未知量,Z 为不便于直接观测的未知量。
设(12)i x i n =、、、 的独立观测值为i l ,其相应的真误差为i x ∆ 。
由于i x ∆的存在,使得函数12(,,,,,)i n Z f x x x x =也产生相应的真误差Z ∆ 。
将12(,,,,,)i n Z f x x x x =取全微分,得到:1212i n inf fffdZ dx dx dx dx x x x x ∂∂∂∂=+++++∂∂∂∂ (1.1)因为误差i x ∆ 以及Z ∆ 都很小,所以在上式中,可以近似用i x ∆ 以及Z∆代替来i dx 以及dZ ,于是有:1212i n inf f ffZ x x x x x x x x ∂∂∂∂∆=∆+∆++∆++∆∂∂∂∂(1.2)上式中ifx ∂∂ 为函数f 对各个自变量的偏导数(12)i n =、、、。
将i i x l = 带入各偏导数中,即为确定的常数,设()i i x l i iff x =∂=∂ ,则 1212i n inf f ffZ x x x x x x x x ∂∂∂∂∆=∆+∆++∆++∆∂∂∂∂ (1.3)可以写成: 1122i i n n Z f x f x f x f x ∆=∆+∆++∆++∆(1.4)为了求得函数与观测值之间的中误差的关系式,设对各i x 进行了k 次观测,则可以写出k 个类似于(1.5)的关系式:(1)(1)(1)(1)(1)1122(2)(2)(2)(2)(2)1122()()()()()1122i i n n i i n n k k k k k i i n n Z f x f x f x f x Z f x f x f x f x Z f x f x f x f x ∆=∆+∆++∆++∆∆=∆+∆++∆++∆∆=∆+∆++∆++∆将以上各式等号两边平方后,再相加,得:2222222221122,1[][][][][]2[]ni i n n i j i j i j i jZ f x f x f x f x f f x x =≠∆=∆+∆++∆++∆+∆∆∑(1.4)[ ]表示求和。




误差传播定律
误差传播定律是机器学习领域中一种重要的定理,它定义了损失函数与网络参数之间的关系。
误差传播定律解释了当网络参数发生变化时,损失函数会发生什么变化。
它提供了一种方法来利用梯度下降(Gradient Descent)算法来优化网络参数,从而最小化整个网络的损失函数值。
误差传播定律表明,可以通过计算每个参数的梯度,来调整网络参数,从而减小损失函数的值,从而达到最优参数的目的。
因此,误差传播定律是深度学习算法训练网络和模型参数的核心理论基础。

误差传播定律
一、误差传播定律(Error Backpropagation Law)
误差传播定律(Error Backpropagation Law)是一种重要的人工神经网络算法,它
最早在1986年被Rumelhart等人提出,并在子后学习过程中发挥着重要作用。
利用反向
传播技术,可以实现多层神经网络,也称为反向传播算法。
误差传播算法通过误差的反馈,以自动化的方式改善网络模型的预测结果。
该算法首
先确定一个初始的权重和偏差,然后根据实际情况,不断增加参数和权重,使它们能够更
好地适应训练样本数据。
针对网络输出结果,通过与预期输出比较,计算出一个误差值,
误差值把权重更新的任务传给神经元,得到一个新的权重,让神经元更加敏感的反应输入,以达到优化网络的效果。
误差传播算法是一种利用梯度下降法以及链式法则(Chain Rule)进行反向传播的数
学方法。
误差的反向传播是指,从神经网络的输出端开始,使用链式法则将误差向输入端
传播,并依次更新每个神经元的权重和偏差,以最大程度地减小输出层表示的网络误差。
该过程反复进行,不断减少最终误差,至最小时,说明模型参数已达到最优解。
综上所述,误差传播算法是一种重要的人工神经网络算法,它利用反向传播技术,以
自动化的方式改善网络模型的预测结果,实现多层神经网络,根据误差的反馈不断增加参
数和权重,进而最大程度减小最终误差,达到最优解。
由于该算法不仅比较简单,而且收
敛速度非常快,所以在现今的深度学习研究中具有重要地位。
第五章误差传播定律5.1误差的来源和分类(板书)经过前面几章的学习,我们掌握了测量的基本工作—测角、量距、测高差的理论和方法。
那么在这些工作中,我们通过测量得到的数据是否就是真实值呢?当然不是,因为在测量工作中,误差总是无处不在的。
在我们的每一次观测中,都包含多种误差存在,因此这一章我们来学习测量中误差的特点及其规律。
一、定义:观测值与真值之间的差值,记为:∆X=i-Lix为真值,即能代表某个客观事物真正大小的数值。
Li为观测值,即对某个客观事物观测得到的数值。
i∆为观测误差,即真误差。
二、误差的来源1、测量仪器一是仪器本身的精度是有限的,不论精度多高的仪器,观测结果总是达不到真值的。
二是仪器在装配、使用的过程中,仪器部件老化、松动或装配不到位使得仪器存在着自身的误差,如水准仪的水准管轴不平行视准轴,使得水准管气泡居中后,视线并不水平。
水准尺刻划不均匀使得读数不准确。
又如经纬仪的视准轴误差、横轴误差、竖盘指标差都是仪器本身的误差。
2、观测者是由于观测者自身的因素所带来的误差,如观测者的视力、观测者的经验甚至观测者的责任心都会影响到测量的结果。
如水准尺倾斜、气泡未严格居中、估读不准确、未精确瞄准目标都是观测误差。
3、外界条件测量工作都是在一定的外界环境下进行的。
例如温度、风力、大气折光、地球曲率、仪器下沉都会对观测结果带来影响。
上述三项合称为观测条件a.等精度观测:在若干次观测中,观测条件相同b.不等精度观测测量误差的分类根据测量误差表现形式不同,误差可分为系统误差、偶然误差和粗差。
1、系统误差定义:误差的符号和大小保持不变或者按一定规律变化,则称其为系统误差。
例:钢尺的尺长误差。
一把钢尺的名义长度为30m ,实际长度为30.005m ,那么用这把钢尺量距时每量一个整尺段距离就量短了5mm ,也就是会带来-5mm 的量距误差,而且量取的距离越长,尺长误差就会越大,因此系统误差具有累计性。
又如水准仪的i 角误差(画图),由于水准管轴与视准轴不平行,两者之间形成了夹角i ,使得中丝在水准尺上的读数不准确。
第五章误差传播定律5.1误差的来源和分类(板书)经过前面几章的学习,我们掌握了测量的基本工作—测角、量距、测高差的理论和方法。
那么在这些工作中,我们通过测量得到的数据是否就是真实值呢?当然不是,因为在测量工作中,误差总是无处不在的。
在我们的每一次观测中,都包含多种误差存在,因此这一章我们来学习测量中误差的特点及其规律。
一、定义:观测值与真值之间的差值,记为:∆=XLii-x为真值,即能代表某个客观事物真正大小的数值。
Li为观测值,即对某个客观事物观测得到的数值。
i∆为观测误差,即真误差。
二、误差的来源1、测量仪器一是仪器本身的精度是有限的,不论精度多高的仪器,观测结果总是达不到真值的。
二是仪器在装配、使用的过程中,仪器部件老化、松动或装配不到位使得仪器存在着自身的误差,如水准仪的水准管轴不平行视准轴,使得水准管气泡居中后,视线并不水平。
水准尺刻划不均匀使得读数不准确。
又如经纬仪的视准轴误差、横轴误差、竖盘指标差都是仪器本身的误差。
2、观测者是由于观测者自身的因素所带来的误差,如观测者的视力、观测者的经验甚至观测者的责任心都会影响到测量的结果。
如水准尺倾斜、气泡未严格居中、估读不准确、未精确瞄准目标都是观测误差。
3、外界条件测量工作都是在一定的外界环境下进行的。
例如温度、风力、大气折光、地球曲率、仪器下沉都会对观测结果带来影响。
上述三项合称为观测条件a.等精度观测:在若干次观测中,观测条件相同b.不等精度观测测量误差的分类根据测量误差表现形式不同,误差可分为系统误差、偶然误差和粗差。
1、系统误差定义:误差的符号和大小保持不变或者按一定规律变化,则称其为系统误差。
例:钢尺的尺长误差。
一把钢尺的名义长度为30m ,实际长度为30.005m ,那么用这把钢尺量距时每量一个整尺段距离就量短了5mm ,也就是会带来-5mm 的量距误差,而且量取的距离越长,尺长误差就会越大,因此系统误差具有累计性。
又如水准仪的i 角误差(画图),由于水准管轴与视准轴不平行,两者之间形成了夹角i ,使得中丝在水准尺上的读数不准确。
第五章误差传播定律第五章误差传播定律5.1误差的来源和分类(板书)经过前面几章的学习,我们掌握了测量的基本工作—测角、量距、测高差的理论和方法。
那么在这些工作中,我们通过测量得到的数据是否就是真实值呢?当然不是,因为在测量工作中,误差总是无处不在的。
在我们的每一次观测中,都包含多种误差存在,因此这一章我们来学习测量中误差的特点及其规律。
一、定义:观测值与真值之间的差值,记为:=∆LiXi-x为真值,即能代表某个客观事物真正大小的数值。
Li为观测值,即对某个客观事物观测得到的数值。
i∆为观测误差,即真误差。
二、误差的来源1、测量仪器一是仪器本身的精度是有限的,不论精度多高的仪器,观测结果总是达不到真值的。
二是仪器在装配、使用的过程中,仪器部件老化、松动或装配不到位使得仪器存在着自身的误差,如水准仪的水准管轴不平行视准轴,使得水准管气泡居中后,视线并不水平。
水准尺刻划不均匀使得读数不准确。
又如经纬仪的视准轴误差、横轴误差、竖盘指标差都是仪器本身的误差。
2、观测者是由于观测者自身的因素所带来的误差,如观测者的视力、观测者的经验甚至观测者的责任心都会影响到测量的结果。
如水准尺倾斜、气泡未严格居中、估读不准确、未精确瞄准目标都是观测误差。
3、外界条件测量工作都是在一定的外界环境下进行的。
例如温度、风力、大气折光、地球曲率、仪器下沉都会对观测结果带来影响。
上述三项合称为观测条件a.等精度观测:在若干次观测中,观测条件相同b.不等精度观测测量误差的分类根据测量误差表现形式不同,误差可分为系统误差、偶然误差和粗差。
1、系统误差定义:误差的符号和大小保持不变或者按一定规律变化,则称其为系统误差。
例:钢尺的尺长误差。
一把钢尺的名义长度为30m,实际长度为30.005m,那么用这把钢尺量距时每量一个整尺段距离就量短了5mm,也就是会带来-5mm的量距误差,而且量取的距离越长,尺长误差就会越大,因此系统误差具有累计性。
又如水准仪的i角误差(画图),由于水准管轴与视准轴不平行,两者之间形成了夹角i,使得中丝在水准尺上的读数不准确。
如果水准仪离水准尺越远,i角误差就会越大。
由于i角误差是有规律的,因此它也是系统误差。
正是由于系统误差具有一定的规律性,因此只要找到这种规律性,就可以通过一定的方法来消除或减弱系统误差的影响。
具体方法有:1.采用观测方法消除:比如水准仪安置距前后水准尺等距的地方可以消除i角误差和地球曲率的影响。
通过后前前后的观测顺序可以减弱水准仪下沉的影响。
通过盘左盘右观测水平角和竖直角可以消除经纬仪的横轴误差、视准轴误差、照准部偏心差和竖盘指标差。
2. 加改正数:例如精密钢尺量距中的尺长改正:∆l d = l/ l 0 ×∆l (l 为任意尺段长)、温度改正和高差改正。
三角高程测量中的球气差改正数:R D f 243.0=,光电测距仪的加常数和乘常数的改正:RD K D +=∆3. 检校仪器:将仪器的系统误差降低到最小限度或限制在一个允许的范围内。
措施:用计算方法加以改正;用一定的观测方法加以消除或削弱;检校仪器以限制误差的范围。
2、偶然误差定义:偶然误差的符号和大小是无规律的,具有偶然性。
例如度盘分划不均匀引起的误差就是偶然误差,因为在度盘上有的地方可能分划的密度大一些,有的地方分划的密度要稀疏一些。
又如我们在读数的时候,最后一位要估读,有时可能估读得大一些,有时估读得小一些,这是没有规律的。
另外还有瞄准误差(照准误差)、对中误差也属于偶然误差。
虽然单个的偶然误差没有规律,但大量的偶然误差具有统计规律。
在后面的内容中就是要专门研究偶然误差的这种统计规律,如果没有特别的说明,后面提到的误差都是偶然误差。
3、粗差也称错误,如瞄错目标、读错、记错数据、算错结果等错误,这个错误大家在实验中都是犯过的。
在严格意义上,粗差并不属于误差的范围。
在测量工作中,粗差可以通过检核——包括测站检核、计算检核以及内业工作阶段的检核发现粗差,并从测量成果中予以剔除(如水平角实验中角度闭合差为十几分)。
而系统误差和偶然误差,是同时存在的。
对于系统误差,通过找到其规律性,采用一定的观测方法来消除或减小。
当系统误差很小,而误差的主要组成为偶然误差时,则可以根据其统计规律进行处理——测量上称为“平差”。
偶然误差的特性1.特性根据前面所讲的,单个偶然误差没有规律性,而在相同条件下的重复观测一个量,也就是等精度观测,经过重复观测所出现的大量的偶然误差具有规律性。
例:在相同条件下,对三角形的三内角进行了独立的重复观测,由于每次观测中都含有误差,所以三角性的三个内角的观测值加起来不会等于真值,真值应该是180度。
设三个内角的观测值加起来为 Li=ai+bi+ci ,即Li 即为观测值(板书)则︒-=∆180Li i ,i ∆为真误差。
现在重复观测了358次,将其真误差的大小按一定的区间统计成一个列表(见书上P93):从这个列表中,我们可以看出偶然误差的几个特性:(注:表格中误差的相对个数指的是误差在每39 25 20 12 1913 0.0~0.5 0.5~总数负误差个数正误差个数 误差所在区间个误差区间内出现的次数除以误差的总次数,比如在0-0.2秒的这个区间内,即第一行,负误差的相对个数0.126应该是45除以358得到的,这个相对个数实际上就是误差出现的频率。
)1、在一定观测条件下,偶然误差的绝对值不会超过一定的界限(有界性);2、绝对值较小的误差比绝对值较大的误差出现的概率大(小误差的密集性);3、绝对值相等的正负误差,出现的机会相等(对称性);4、由第3条特性可知,当n→∞时,偶然误差的算术平均值→0(即数学期望), 即0][lim ...lim )(21=∆=∆++∆+∆=∆∞→∞→n n n E n n (抵偿性)。
([]符号表示求和)(数学期望定义:随机变量X 的观察值的算术平均值为随机变量X 的数学期望)2.直方图由统计表格的数据我们可以绘制出一个直方图,其中横坐标为误差的大小,纵坐标为误差在每个区间出现的频率,即以∆=d nk y /,∆d 代表误差区间。
3.正态分布曲线当n→∞,也就是观测的次数趋近无穷多次,并且∆d →0时也就是误差区间无穷小时,直方图中各个小长条矩形组成的折线就会变成一条曲线,这条曲线是一条正态分布曲线,可用正态分布概率密度函数表示:22221)(σσπ∆-=∆=e f y我们回忆一下概率统计中所学的有关正态分布的内容:随机变量X 服从参数为μ、σ的正态分布函数标准形式为: 222)(21)(σμσπ--==x e x f y ,其中μ为随机变量X 的数学期望,σ为随机变量X 的标准差)(x D (均方差),σ2为方差)(x D 。
因此上面的函数中,误差∆为真误差,∆是一个随机变量,因∆是偶然误差。
μ=0,因可化为2)0(-∆的形式,即随机变量∆的数学期望为0,σ为随机变量σ的标准差。
方差的数学意义为:反映随机变量∆与其均值)(∆E ,即与其数学期望的偏离程度。
由于σ2就是∆的方差,显然σ2与观测条件有关,如果观测条件越好,则误差∆就应该越小,就越接近于0,也就是越接近于数学期望,由于∆与数学期望的偏离程度越小,从而σ2越小。
我们再看看有关精度的内容。
5.2 衡量精度的标准一、精度的含义所谓精度,是指误差分布的集中与离散程度。
如误差分布集中(曲线a ),则观测精度高;若误差分布离散(曲线b ),则观测精度就低。
(画图)从我们前面的分析可以知道,误差分布的集中与离散程度可以用方差σ2或标准差σ来表示。
如果σ越小,误差偏离数学期望的程度就越低,则误差集中程度就会越高,即精度越高,反之如果σ越大,则误差的离散程度越高,精度越低,因此我们可以用σ即用标准差来衡量观测的精度。
二、中误差(均方差)在测量工作中,我们就是用标准差来衡量观测精度的,我们称之为中误差,用m 表示。
设在相同的观测条件下,对未知量进行重复独立观测,观测值为:l 1,l 2,…,l n ,其真误差为: ⊿1,⊿2,…,⊿n则真误差的方差:nE E E D n ][lim)()]([)(222∆∆=∆=∆-∆==∆∞→σ式中当n→∞,)(∆E =0,根据数学期望的定义)(2∆E 就是2∆的算术平均值。
[ ]为累加符号,n n ∆∆++∆∆+∆∆=∆∆...][2211真误差的标准差: nD n ][lim)(∆∆±==∆±∞→σ (无穷次)实际工作中,观测次数有限,故取标准差的估值作为中误差:nm ][ˆ∆∆±==σ(有限次)应用时应注意:1、⊿i 可以是对一个量n 次同精度观测,亦可以是对n 个量各进行一次同精度观测的误差(例1:在全站仪测距时有的同学说测出来的距离不断地在变化,这实际上是全站仪在不断地测距,也就是对一个量——这个量就是距离——进行了多次等精度观测,而每次的观测值都有误差存在,误差有时大,有时小,所以测出来的距离值不断在变化。
例2:在前面讲的方向法测水平角时(画图),需要对多个方向观测,先瞄A ,再瞄B ,再瞄C …,这实际上就是对n 个量进行了一次等精度观测);2、中误差m 是衡量一组观测的精度标准,个别误差的大小并不能反映精度的高低;3、n 较大时,m 较可靠;n 有限时,m 仅做参考;4、m 前要冠以±号,并有计量单位。
5、m 为中误差,∆为真误差,不要混淆。
例题1设甲乙两组观测,真误差为: 甲:+4”,+3”,0”,-2”,-4”; 乙:+6”,+1”,0”,-1”,-5” 试比较两组的精度。
解:"0.351640916±+++±=+=甲m"5.35251136±+++±==乙m因此甲组的精度高。
中误差的性质1. 中误差表示误差分布的离散度。
(中误差就是标准差,而标准差就是表示误差分布离散度的。
2. 等精度观测中,中误差表示一组观测值的精度,也表示单个观测值的精度。
(如上例中甲组中误差为±3.0”,同时甲组单个观测值的中误差也为±3.0”) 3. 概率特性。
{}{}6826.0=+<∆<-=+<∆<-σσσμσμP Pμ为误差的数学期望,因此μ=0。
此公式表示真误差在(-σ,+σ)内出现的概率。
这个概率的计算在概率统计那本书中写了其过程。
(在“方差”的那一章节) 我们还可计算得: {}9544.022=+<∆<-σσP{}9974.033=+<∆<-σσP我们可以看到,对于真误差∆来说,它的值落在区间[-3σ,+3σ]几乎是肯定的事。
因此在测量工作中,我们常常取三倍中误差作为偶然误差的容许值(或限差),如果精度要求较高时,就可以取两倍中误差作为限差,即 m m 23或=容∆三、相对误差1.相对中误差假设现在丈量了两段距离: 甲: 100米,=甲m ±0.01m乙: 200米,=乙m ±0.01m到底那组的精度高些呢?如果从中误差来看,两组的精度相等,但这样显然不合理。