协方差传播律当σxy=时表示这两个观测值的误差之间互不影响
- 格式:ppt
- 大小:2.44 MB
- 文档页数:67


平差知识点总结(总10页) -CAL-FENGHAI.-(YICAI)-CompanY One 1-CAL-本页仅作为文档封面,使甬请直接删除测量平差知识点观测误差包括:粗差、系统误差、偶然误差。
粗差:即粗大误差,或者说是一种大量级的误观测差,是由观测过程中的差错造成的。
发现粗差的方法:进行必要的重复测量或多余观测,采用必要而又严格的检核、验算等,发现后舍弃或重测。
系统误差:在相同条件下进行一系列观测,如果误差在大小、符号表现出一致性,或者在观测过程中按一定的规律变化,或者为一常数,这种误差称为系统误差。
消除或削弱的方法:采取合理的操作程序(正、倒镜,中间法,对向观测等);用公式改正,即加改正裁(如钢尺量距时的尺长误差等)。
偶然误差:在相同条件下进行一系列观测,如果误差在大小、符号上表现出偶然性,即就单个误差而言,该误差的大小和符号没有规律性,但就大量误差的总体而言,具有一定的统计规律,这种误差称为偶然误差,或者随机误差。
采臥措施:处理带仔偶然误差的观测值,就是木课程的内容,也叫做测量平差。
偶然谋差又称随机误差,有以I、•四个特性:1)一定观测条件下,误差绝对值有一泄限值(有限性);2)绝对•值较小的课差比绝对值较人的课差出现概率人(渐降性):3)绝对值相等的正负误差出现概率相同(对称性);4)偶然谋差的数学期望为零(抵偿性)。
衡量精度的指标有五个,分别眉中矗、平均矗、或然i灵差、极限i灵差以及相对中谋差。
其中中矗和极限误差以及相对中保差是工程測量中常用的指标。
5、相对谋差颠差、屮促差、极限促差等指标,对于菜些观测结果,有时还•侮全表达观测结果的好坏,例如,分别丈1000m及500⑴的两段距离,它们的中课差均为±2cn】,虽然两者■的中误差相同,但就M位长度而言,两者精度并彳、相同。
显然询耆的郴对蒂度比后者耍高。
一般:而言,一些与长度有关的观测俺或其函数值,单纯用中误苣还不能区分出蒂度的高低,所以常用相对课差。


测量不确定度基本知识培训测验题李正东编姓名一.填空题成绩1.在一定的条件下事物的因果关系是确定的事件被称为事件,而在一定的条件下结果不可预知的事件被称为事件,也称事件。
2.随机变量具有的二个特点是性和性。
3.随机变量的特征值包括、、和等。
4.表示随机变量本身大小的取值中心,也称。
其估计值为一系列测量结果的。
5.测量误差是和之差,测量误差也称之为误差。
6.相对误差是除以所得之商。
7.误差通常按其性质和产生的原因,可分为误差、误差和误差三类。
8.在同一量的多次测量过程中,保持恒定或以可预知方式变化的测量误差的分量,被称之为误差。
9.在同一量的多次测量过程中,以不可预知的方式变化的测量误差分量,被称之为误差。
10.给定条件下,误差明显超出了预期值,被称之为误差,或称误差。
11.为消除或减小测量结果的系统误差,应将值与未修正的测量结果用法相加。
12.在相同的测量条件下,增加测量次数,取其平均值可以减小测量结果的误差,但不能消除误差。
13.测量不确定度是表征合理地赋予被测量之值的,与测量结果相关联的。
14.标准不确定度是以表示的测量不确定度,数学符号为。
15.评定标准不确定度的方法有两类:A类评定是用对一列观测值进行的方法来评定标准不确定度;B类评定是用的方法来评定标准不确定度。
任何一个不确定度分量既可以用A类评定法评定,也可以用B类评定法评定。
16.引起测量不确定度的因素可分为影响和影响两类。
但不要因此把用A类方法评定的不确定度错误地称为不确定度,亦不要把用B类方法评定不确定度错误地称为不确定度。
17.当测量结果是由若干个其它量的值求得时,按其它各量的和算得的标准不确定度,被称之为不确定度,它是测量结果的估计值,数学符号为。
18.计算合成标准不确定度应按定律计算,当各输入量彼此不相关时,协方差u ,式中的被称为灵敏度系数。
项等于,其数学表达式为c该数值的大小反映了对合成标准不确定度的影响程度。
19.为使测量结果以更高的置信概率落在某量值区间内,将合成标准不确定度乘以2~3的数字因子,该因子称之为因子,乘以该因子后的不确定度称之为不确定度,数学符号为。



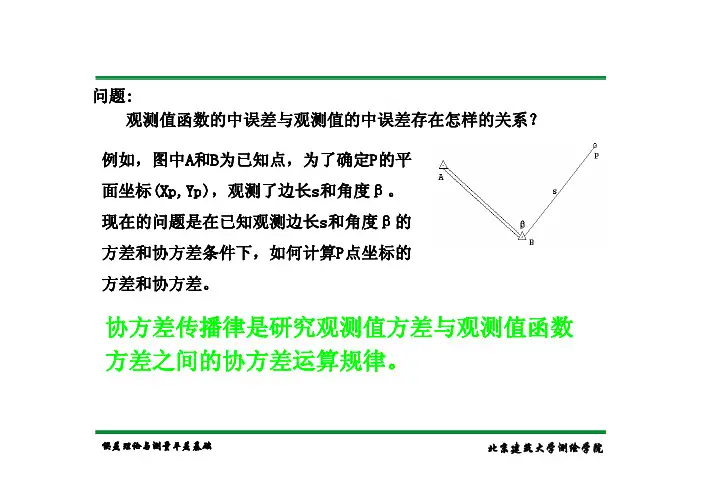


协方差传播律1. 引言协方差是统计学中用来衡量两个随机变量之间关系的指标。
在金融领域,协方差被广泛应用于风险管理和资产组合优化等方面。
协方差传播律(Covariance Propagation Law)是指在多个随机变量之间存在关联时,如何计算它们之间的协方差。
2. 协方差的定义和性质协方差衡量了两个随机变量之间的线性关系程度。
对于两个随机变量X和Y,其协方差定义为:Cov(X,Y)=∑(X i−X‾)ni=1(Y i−Y‾)n−1其中,X i和Y i分别表示第i次观测到的X和Y的取值,X‾和Y‾分别表示X和Y的均值。
协方差具有以下性质:•对称性:Cov(X,Y)=Cov(Y,X)•线性性:Cov(aX+bY,Z)=a Cov(X,Z)+b Cov(Y,Z),其中a和b为常数,X、Y和Z为随机变量。
3. 协方差传播律的推导在实际问题中,我们经常需要计算多个随机变量之间的关系。
假设有n个随机变量X1,X2,...,X n,它们与另一个随机变量Y之间存在关联。
我们希望计算Y与这n个随机变量的协方差。
根据协方差的线性性质,我们可以将Y表示为这n个随机变量的线性组合:Y=a1X1+a2X2+...+a n X n其中a1,a2,...,a n为常数。
现在我们来计算Y与任意两个随机变量X i和X j之间的协方差Cov(Y,X i)和Cov(Y,X j)。
根据协方差的定义:Cov(Y,X i)=∑(Y k−Y‾)mk=1(X ik−X i‾)m−1其中,Y k表示第k次观测到的Y的取值,X ik表示第k次观测到的X i的取值,Y‾和X i‾分别表示Y和X i的均值,m为样本数量。
将Y的表达式代入上述公式:Cov(Y,X i)=∑(a1X1k+a2X2k+...+a n X nk−Y‾)mk=1(X ik−X i‾)m−1展开并整理上式:Cov(Y,X i)=a1∑(X1k−X1‾)mk=1(X ik−X i‾)m−1+a2∑(X2k−X2‾)mk=1(X ik−X i‾)m−1+...+a n∑(X nk−X n‾)mk=1(X ik−X i‾)m−1可以看出,Cov(Y,X i)可以表示为n个随机变量X j与X i之间协方差的线性组合。

协方差传播律协方差传播律指的是在多变量情况下怎么计算协方差。
协方差是衡量两个变量之间关系的统计度量,我们可以通过协方差矩阵分析多个变量之间的相互作用。
在多变量情况下,协方差传播律有很重要的作用,因为很多时候我们需要计算多个变量之间的协方差。
以下是协方差传播律的具体解释:假设有一个由多个变量组成的向量x,对应一个方差-协方差矩阵S,而且还有一个由x组成的函数y = f(x),那么y对应的方差、协方差矩阵可以通过以下方式计算:Var(y) = J*S*J',Cov(y) = J*S其中,J是一个m×n的Jacobian矩阵,m是y的维度,n是x的维度。
J由y对x每个元素的一阶偏导数组成。
这些公式可能看起来比较复杂,但实际上非常简单。
举个例子,如果我们有两个变量x和y,它们之间有一个函数z = x + y,那么z 的协方差矩阵可以通过以下方式求解:⎡ Var(x) Cov(x,y) ⎡⎡⎡⎡ Cov(y,x) Var(y) ⎡其中Var(x)是x的方差,Var(y)是y的方差,Cov(x,y)和Cov(y,x)是x和y之间的协方差。
在实际应用中,协方差传播律可以帮助我们解决很多问题。
比如,假设我们有一个模型,它包含多个变量,我们想要在这个模型的基础上进行优化,那么我们需要知道每个变量对模型的影响。
这时协方差传播律就派上用场了。
我们可以利用这个公式计算每个变量的方差和协方差,从而分析出它们对模型的重要性,并确定优化方向。
总之,协方差传播律是多变量统计分析中不可或缺的工具,通过它,我们可以更加深入地了解变量之间的相互作用,进一步优化我们的统计分析和预测模型。
考试复习重点资料(最新版)资料见第二页封面第1页第一章测量误差理论§1-1正态分布概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。
一、一维正态分布§1-2偶然误差的规律性2.直方图由表2-1、表2-2可以得到直方图2-1和图2-2(注意纵、横坐标各表示什么?),直方图形象地表示了误差分布情况。
3.误差分布曲线(误差的概率分布曲线)在一定的观测条件下得到一组独立的误差,对应着一种确定的误差分布。
当观测值个数的情况下,频率稳定,误差区间间隔无限缩小,图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线,称为误差分布曲线,随着n增大,以正态分布为其极限。
因此,在以后的讨论中,都是以正态分布作为描述偶然误差分布的数学模型。
4.偶然误差的特性第2章协方差传播律在测量实际工作中,往往会遇到某些量的大小并不是直接测定的,而是由观测值通过一定的函数关系间接计算出来的,显然,这些量是观测值的函数。
例如,在一个三角形中同精度观测了3个内角L1,L2和L3,其闭合差w和各角度的平差值分别又如图3—1中用侧方交会求交会点的坐标等。
现在提出这样一个问题:观测值函数的精度如何评定?其中误差与观测值的中误差存在怎样的关系?如何从后者得到前者?这是本章所要讨论的重要内容,阐述这种关系的公式称为协方差传播律。
§2—1数学期望的传播数学期望是描述随机变量的数字特征之一,在以后的公式推导中经常要用到它,因此,首先介绍数学期望的定义和运算公式。
其定义是:§2—2协方差传播律从测量工作的现状可以看出:观测值函数与观测值之间的关系可分为以下3种情况,下面就按这3种情况来讨论两者之间中误差的关系。
第3章最小二乘平差§3-1条件平差原理以条件方程为函数模型的方法称之条件平差。
二、按条件平差求平差值的计算步骤及示例计算步骤:1.列出r=n-t个条件方程;2.组成并解算法方程;3.计算V和的值;4.检核。
协方差计算法则
协方差计算是互联网研究的重要计算统计技术,它可以用来比较多个不同的变量,以便更好地对数据在不同方面的变化进行评估。
协方差计算的基本思想是比较不同的变量的方差,以及两个变量之间的协方差,以更深入地了解这些变量之间的关系。
要正确计算协方差,首先需要计算两个变量x和y之间的平均值μx和μy,
其次计算x和y之间的均方差σx2和σy2,最后计算x和y之间的协方差σxy。
协方差的正负号代表x和y之间的相关性,正的协方差表示x和y的值增加或减少时,x和y的值也会增加或减少,而负的协方差表示x和y的值增加或减少时,x
和y的值会相反地变化。
协方差计算可以帮助互联网研究人员识别数据中可能存在的联系。
例如,研究
人员可以使用协方差计算来分析网站上的用户访问量和搜索走势之间的关系,从而推测出让用户更加满意的网站结构。
除此之外,研究人员还可以使用协方差计算来分析社交媒体用户的表现和其他民意的季节性变化。
这有助于他们更好地判断社交媒体和政治倾向之间的关系。
总而言之,协方差计算是互联网研究的重要计算技术,它有助于我们更深入地
了解网站结构和社交媒体等特定变量之间的关系,并利用此信息来完善系统设计和政策制定。
通过正确地计算协方差,我们将得到更好的互联网应用和政策执行效果。