当前位置：文档之家 › 误差理论与测量平差基础第三章 协方差传播律及权

误差理论与测量平差基础第三章 协方差传播律及权

  • 格式：ppt
  • 大小：466.50 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

测量平差 第三章

测量平差 第三章
可得：
DYY F DXX F
2 Y rr rn nn
T
nr
Y关于Z的互协方差阵：
DYZ E Y EY Z EZ F DXX K
T rt rn nn


T
nt
例3：在一个三角形中，同精度独立观测得到三个内 角L1、L2、L3，其中误差为，将闭合差平均分配后 各角的协方差阵。
2 2 h S km
h S km
其估值公式为
ˆ ˆ ˆ2 ˆ2 h S km h S km
例题
水准测量中若要求每公里观测高差中误差不超过 10mm，水准路线全长高差中误差不超过60mm, 则该 水准路线长度不应超过多少公里？ 解：由公式
2 2 h S km
差的关系。
一、观测值线性函数的方差
设有n维观测向量X，其数学期望μ和协方差阵分别为：
设有n维观测向量X的函数Z为：Z=KX+K0,求DZZ＝？ 式中K为系数阵，K0为常数。 根据方差的定义得：
2 DZZ Z E Z EZ Z EZ

T

2 DZZ Z KDXX K T
应用协方差传播公式得

2 L
2
n L n
例题
已知某台经纬仪一测回的测角中误差为±6'',如 果要使各测回的平均值的中误差不超过±2'',则至少 应测多少测回？ 解：由公式
2 x
2
N
可得
2 62 N 2 2 9 x 2
答：至少应测9测回
三、若干独立误差的联合影响
B
mp
mu ms

A
s

第3章：《误差理论与测量平差基础》 - 山东科技大学泰安校区

第3章：《误差理论与测量平差基础》 - 山东科技大学泰安校区
f k0 f ( X 1 , X 2 , X ) ( )0 X i0 i 1 X i
0 0 0 n n
Z [k 1 , k 2 , kn ] X k0 KX k0
n ,1
DZZ KDXX K
T
例4、根据极坐标法测设P点的坐标，设已知 点无误差，测角中误差为m，边长中误差ms， 试推导P点的点位中误差。
2 j 2 0
Qii为Li的协因数。
Q jj为L j的协因数。
Qij为Li关于L j的协因数 或相关权倒数。
1 ji Qij 2 pi 0
变换形式为：
2 i2 0 Qii 2 2 j 0 Q jj 2 ji 0 Qij
不难得出：
DXX
12 12 1n Q11 Q12 Q1n Q 2 Q22 Q2 n 21 2 2 n 2 21 0 2 Qn1 Qn 2 Qnn n1 n 2 n
山东科技大学山东科技大学资源与土木工程系资源与土木工程系误差理论与测量平差基础第六章附有参数的条件平差第二章误差分布与精度指标第三章协方差传播律及权第五章条件平差第七章间接平差第一章绪论第八章附有限制条件的间接平差第九章概括平差函数模型第十章误差椭圆第四章平差数学模型与最小二乘原理教材内容第十二章近代平差概论第一节协方差传播律第二节协方差传播律的应用第三节权与定权的常用方法第四节第五节协因数传播律第六节由真误差计算中误差及其实际应用直接观测值间接观测值函数关系具有一定精度也应该具有一定精度根据函数关系提出问题
2 (二) 选定了 0 ，即对应一组权。
（三）权是衡量精度的相对指标，为了使权起到比较 精度的作用，一个问题只选一个0。

误差理论与平差基础-第3章 协方差传播率及权

误差理论与平差基础-第3章 协方差传播率及权

2 0 0 2 DLL 0 0 2 0 0
2 0 0 2 / 3 1 / 3 1 / 3 2 / 3 1 / 3 1 / 3 1 / 3 2 / 3 1 / 3 0 2 0 1 / 3 2 / 3 1 / 3 DL ˆL ˆ 2 1 / 3 1 / 3 2 / 3 0 0 1 / 3 1 / 3 2 / 3

106.1 7.8 121 2.6 6.8 244.3
二、协方差传播律
2、线性函数的方差——协方差
[例7] 求等精度观测的三角形三个内角按照闭合差分配后角 度的协方差阵。 三角形闭合差: w 180 L1 L2 L3
1 2 1 1 ˆ L1 L1 W L1 L2 L3 60 3 3 3 3 1 1 2 1 ˆ L2 L2 W L1 L2 L3 60 3 3 3 3 ˆ L 1 W 1 L 1 L 2 L 60 L 3 3 1 2 3 3 3 3 3

a1( X A X s ) b1 (YA YS ) c1 ( Z A Z S ) a3 ( X A X S ) b3 (YA YS ) c3 ( Z A Z S )
a 2 ( X A X s ) b2 (YA YS ) c2 ( Z A Z S ) a3 ( X A X S ) b3 (YA YS ) c3 ( Z A Z S )
XY
XY XY
表示X、Y 间互不相关，对于 正态分布而言，相互独立。
YX XY 0
YX XY 0
表示X、Y 间相关。
二、协方差传播律

第三章协方差传播律及权

第三章协方差传播律及权
= E K ( X − µ X )( X − µ X ) T K T
[
[
]
= KE ( X − µ X )( X − µ X ) T K T
[
]
]
]
协方差传播律
DZZ = σ = KDXX K
2 Z
T
DZZ
的纯量形式：
+ L + 2k1 k nσ 1n + L + 2k n −1 k nσ n −1, n
s = ab
先取对数然后再全微分能简化计算。 先取对数然后再全微分能简化计算。 对函数式取自然对数： 对函数式取自然对数：
σ S = 500σ d = 500 × (±0.2) = ±100mm = ±0.1m
最后写成: 最后写成
S = 11.7 ± 0.1 m
回到首页
二、多个观测值线性函数的协方差阵 推导过程： 推导过程：Z = K X + K 函数：
t ,1 t , n n ,1 0 t ,1
E ( Z ) = E ( KX + K 0 ) = Kµ x + K 0
X 0 = X 10
n ,1
[
0 X2
L
X
0 T n
]
0 0 Z = f ( X 10 , X 2 , L , X n ) + (
∂f 0 +( )0 ( X 2 − X 2 ) + L ∂X 2 ∂f 0 +( ) 0 ( X n − X n ) + (二次以上项） ∂X n
∂f ) 0 ( X 1 − X 10 ) dX = ( dX 1 dX 2 L dX n ) T ∂X 1 0 0 dZ = Z − Z 0 = Z − f (X 10 , X 2 , L , X n )

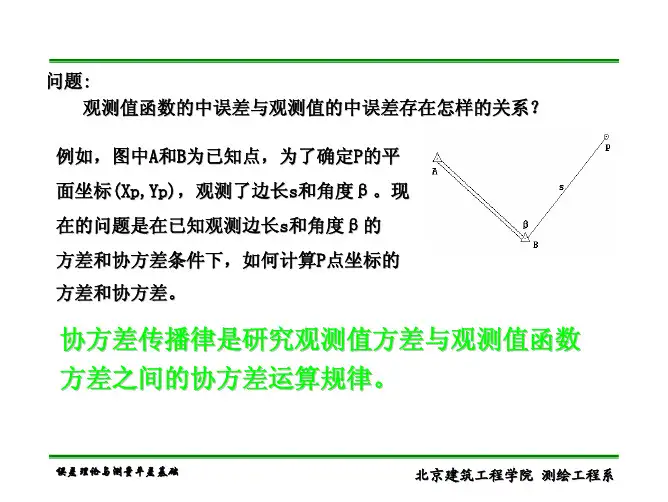
测量平差 第三章 误差传播律与权

测量平差 第三章 误差传播律与权
1 2 n
1
σX X 2 σX
1 2
2
σX X ⎤ ⎥ σX X ⎥
1 n 2 n
1
σX
nX2
2 σX
n
⎥ ⎥ ⎥ ⎦
⎡ μY1 ⎤ ⎡ E (Y1 ) ⎤ ⎡Y1 ⎤ ⎢ ⎥ ⎢ ⎥ ⎢Y ⎥ ⎢ μY2 ⎥ = ⎢ E (Y2 )⎥ Y = ⎢ 2 ⎥ μY = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ μYr ⎥ ⎣ E (Yr ) ⎦ ⎣ ⎦ ⎣Yr ⎦
误差理论与测量平差基础
北京建筑工程学院 测绘工程系
把观测值函数表示为矩阵形式
⎡L ⎤ 1 2 1 1⎤ ⎢ ⎥ ˆ ⎡ L = ⎢ − − ⎥ ⎢L2 ⎥ +60 1 ⎣3 3 3⎦ ⎢L3 ⎥ ⎣ ⎦
⎡2 ˆ ⎡L ⎤ ⎢ 3 1 ⎢ ⎥ ⎢ 1 ˆ ˆ L = ⎢L2 ⎥ = ⎢− ⎢ˆ ⎥ ⎢ 3 ⎢L3 ⎥ ⎢ 1 ⎣ ⎦ ⎢ − ⎢ 3 ⎣
β ，其中误差 β 2
B
A
β1 β2 x
α
C
误差理论与测量平差基础
北京建筑工程学院 测绘工程系
1. 把已知条件写成矩阵、向量形式
⎡ β1 ⎤ β =⎢ ⎥ ⎣ β2 ⎦
⎡ σ 12 σ 12 ⎤ ⎡1.96 −1 ⎤ =⎢ = 2⎥ σ 21 σ 2 ⎦ ⎢ −1 1.96 ⎥ ⎣ ⎦ ⎣
观测量
方差
DXX
⎡1 = σ = KDLL K = ⎢ ⎣7
2 X T
2 7
σ X = 0.84 = 0.9mm
误差理论与测量平差基础
北京建筑工程学院 测绘工程系
协方差计算步骤：
D X X
希望同学们把它记下来

第三章_协方差传播律及权

第三章_协方差传播律及权

(3-2-6)
通常将（ ）、（3-2-5）和（3-2-6）诸式称为协方差传播律。 协方差传播律。 通常将（3-2-4）、（ ）、（ ） ）诸式称为协方差传播律 其中（ 其中（3-2-6）式是（3-2-5）式的特例。 ）式是（ ）式的特例。
的地图上， 【例题1】在1:500的地图上，量得某两点间的距离是d = 23.4 mm，d的量距 例题 】 的地图上 的量距 求两点间的实地距离S和其精度 和其精度σ 误差是 σ d = ±0.2 mm 。求两点间的实地距离 和其精度 S。 解：
第三章
协方差传播律及权
本章学习要点： 本章学习要点： 1、数学期望的传播 、 2、协方差传播定律 、 3、协因数和协因数传播律 、 4、由真误差计算中误差的方法 、 5、系统误差的传播 、
在实际测量工作中，往往有些未知量不是直接测定， 在实际测量工作中，往往有些未知量不是直接测定，而是由观测值 按一定函数关系计算出来的，即某些未知量是直接观测值的函数。 按一定函数关系计算出来的，即某些未知量是直接观测值的函数。
1.96 − 1 − 1 = 1.92( ′′)2 σ = KDββ K = (− 1 − 1) − 1 1.96 − 1
2 x T
σ x = ±1.4 ′′
图3-2
二、多个观测值线性函数的协方差阵 1、 设有观测值 X，它的数学期望 µX与协方差阵DXX ， n1
D XX
σ 12 σ 12 2 σ 21 σ 2 = L L σ n1 σ n 2
L σ 1n L σ 2n L L 2 L σn
(3-2-7)
L k1n k10 L k2n k , K0 = 20 , L L t 1 M L ktn kt 0

《误差理论与测量平差基础》第三章

《误差理论与测量平差基础》第三章

1n 2n 2 n
§3.1 协方差传播律
设有t个 X 的线性函数： n ,1 Z1 k11 X 1 k12 X 2 k1n X n k10 Z 2 k 21 X 1 k 22 X 2 k 2 n X n k 20 Z t k t1 X 1 k t 2 X 2 k tn X n k t 0
E ( Z ) E ( KX k0 ) KE( X ) k0 K X k0
Z的方差为： DZZ E Z E ( Z )Z E ( Z )
E ( KX k 0 K X k 0 )( KX k 0 K X k 0 )
E K ( X X )( X X )T K T
Z K X K0
t ,1 t , n n ,1 t ,1
E ( Z ) E ( KX K 0 ) K x K 0
D ZZ E[( Z E ( Z ))( Z E ( Z )) T ]
t ,t
E[( KX K x )( KX K x ) T ]
KE[( X x )( X x ) T ]K T
T
§3.1 协方差传播律
例3-4 在一个三角形中，同精度独立观测得到
三个内角L1、L2、L3，其中误差均为，将
闭合差平均分配后各角的协方差阵。 例3-5 设有函数： 已知:
Z F1 X F1 Y
t ,1 t , n n ,1
t , r r ,1
DXX、DYY 和DXY DZZ、DZX 和DZY
DYZ E[(Y E (Y ))( Z E (Z )) ]
T r ,t

《测量平差》教案第三章协方差传播律及权(武汉大学版)(中职教育).doc

《测量平差》教案第三章协方差传播律及权(武汉大学版)(中职教育).doc

《测量平差》教案第三章协方差传播律及权第一节数学期望的传播律£(C) = C;E(CX) = CE(X);口/+/+…+ X”)二E(XJ + E(X2)+…+ E(X“)；当X，相互独立时(匸1,2,…,n),E(X“X2,…,XJ = E(XJE(X2)・・・E(XJ第二节协方差传播律协方差传播律是观测值(向量)与其函数(向量)之间精度传递的规律。

一误差的传递1、线性函数课差的传递y = f l x l+f2x2+... + f n x n+f0△F =—\ +/2亠2 + …+推导上述公式，讲解式中符号的含义2、非线性函数误差的传递Y = f(X l X2…兀J+ A A.t+•••+/”△陰2推导上述公式，讲解式中符号的含义3、函数向量误差的传递Y=FX+F0Y=F(X)A Y=F A x讲解式中符号的含义，强调矩阵表达式与纯量表达式之间的相互表式二、协方差的传递1、基木公式函数向量Y=F(X)Z=K(X)其误差向量为A Z=K A X则随机向量与其函数向量间的方差传递公式为Dy = F D X F TDy = K D X K TDy Z = F D X K TD Z y = K D x F1证明第一、第三式，并说明同理可证二、四式。

2独立观测量函数的方差传递/F D x F r= f»f»^f^讲解式中符号的含义，说明公式应用的条件，强调公式的重耍性。

3、分块向量函数向量的方差传递x「Z - 口t+rA ~ Yr,\Dx D X yD z = F t,rDyx Dxr,f r.r证明上式，对阵中元素加以说明，给出两向量不相关时该矩阵的形式。

通过五个典型例题的讲解说明方差■协方差传播公式的应用方法和计算中需注意的问题。

小结：协方差传播律是观测值（向量）与英函数（向量）之间精度传递的规律，用其解决观测值两数（向量）的精度评定问题。

木节重点是利用协方差传播律解题的方法和步骤，以及只有一个观测值函数，且观测值之间不相关时的协方差传播公式的应用。

第3章 协方差传播律及权

第3章 协方差传播律及权
协方差传播律及权
误差理论与测量平差
1 2 3 4 5 6 7 8 9
10
介绍协方差传播律公式及 其应用，权的定义，定权的常用 方法 ，协因数(阵)、权阵的计算 ，协因数传播律公式的应用 ， 利用真误差计算中误差的方法， 需重点掌握。
1 /63
主页
协方差传播律及权
误差理论与测量平差
本章主要内容
1 2 3 4 5 6 7 8 9
2) X、Y表达为同一向量的函数
1 2 3 4 5 6 7 8 9
10
X IX 0Y I
Y 0 X IY 0
X 0 Y
X I Y
由协方差传播律得：
DZX A1 DZY A1 DX A2 DYX DX A2 DYX D XY I A1 D X A2 DYX DY 0 D XY 0 A1 D XY A2 DY DY I
10
解: 1) 将函数式改写为:
Z A 1X A 2Y A 0 A 1 X A2 A0 KU A0 Y
式中
K A 1
X A2 , U Y
由方差阵的定义，即可写出U的方差阵为: 由协方差传播律得：
DX DU DYX DXY DY
10
例 1 设有函数Y=4x1-3x2-60, 已知X(= x1 的方差阵为： 7 2 2
x2
T
)
D
X
2 3
cm
试求Y的方差 。
2 Y
解: 将函数写成矩阵形式，即
Y 4x1 3x2 60 4 3x1 x2 60
T

误差理论与测量平差基础第三章协方差传播律及权

误差理论与测量平差基础第三章协方差传播律及权
参数估计
参数估计可采用最小二乘法或加权最小二乘法。在选择方 法时，需根据实际问题的特点和需求进行权衡。
算法性能评估指标选取
精度指标
精度指标是衡量算法性能的重要指标之一。常用的精度指标包括均方误差、均方根误差、 中误差等，可用于评估算法的估计精度和稳定性。
可靠性指标
可靠性指标用于评估算法在复杂环境和噪声干扰下的性能表现。常用的可靠性指标包括失 败率、误警率、漏警率等。
误差传递规律探讨
误差传递概念
在测量过程中，由于各种因素的影响，观测值会存在一定 的误差。这些误差在传播过程中会遵循一定的规律，即误 差传递规律。
线性函数误差传递
对于线性函数Z=aX+bY（其中a、b为常数），其误差传 递公式为D(Z)=a^2D(X)+b^2D(Y)+2abcov(X,Y)。可以 看出，误差传递与观测值的方差和协方差有关。
的线性相关程度。
对称性
Cov(X,Y) = Cov(Y,X)
加法性
Cov(aX+b, cY+d) = acCov(X,Y)
独立性
若X与Y独立，则Cov(X,Y) = 0
传播律意义与作用
传播律意义
协方差传播律描述了随机变量经过线 性变换后，其协方差矩阵如何变化。 这对于理解和分析复杂系统的误差传 递机制具有重要意义。
权重因子的选择应根据实际情况和测量任务的要求进行，要综合考虑观测值的 精度、稳定性、可靠性等因素。
使用方法
在平差计算中，应根据所选权重因子对观测值进行加权处理，以充分利用观测 值的信息并提高平差结果的精度和可靠性。同时，要注意避免过度加权或欠加 权的情况，以免对结果产生不良影响。
04
基于协方差传播律和权的平差算法设

误差平差：协方差传播定律及权

误差平差：协方差传播定律及权

非线性函数的线性化
如果函数 f ( x) 在 x 0的某一邻域内具有直到n+1阶的导数，则 在该邻域内 f ( x) 的泰勒公式为
f ′′(x0 ) f (x) = f (x0 ) + f ′(x0 )(x − x0 ) + (x − x0 )2 +L 2! f (n) (x0 ) + (x − x0 )n +L +L n!
故：
D = [ F 0] DXX [ 0 K] YZ = FD KT 12
T
协方差传播律小节 求函数（也可是向量）的方差（方差阵）； 求函数（也可是向量）的方差（方差阵）； 适用于各观测为相关观测情况； 适用于各观测为相关观测情况； 定律的通式为： 定律的通式为：
若 则
F = KX + K 0 DFF = KDXX K
L
1
ˆ
L2
ˆ
L3
1 8 00 3（ L1 + L2 + L3 − = L− ） 1 1 8 00 3 ） = L2 − （ L1 + L2 + L3 − 1 1 8 00 3 − （ L + L2 + L3 − 1 3 = L ）
1
试求各函数的方差
ˆ σ L，σ Lˆ ，σ
1 2
ˆ
L 3
DLˆ Lˆ
误差理论与测量平差基础
—协方差传播定律及权
第三章 协方差传播律及权
本章内容包括： 本章内容包括：
§3-1 §3-2 §3-3 §3-4 §3-5 §3-6 数学期望的传播 协方差传播律 协方差传播律的应用 权与定权的常用方法 协因数和协因数传播律 由真误差计算中误差及其实际应用

834误差理论与测量平差基础大纲(2012年版)

834误差理论与测量平差基础大纲(2012年版)

《误差理论与测量平差基础》考研复习大纲（2012年）第一章、绪论（4分）了解系统误差、偶然误差、粗差及其处理方法；掌握测量平差学科的研究对象；理解测量平差任务；了解本课程的任务和内容。

第二章、误差分布与精度指标（6分）理解偶然误差的特性；掌握衡量精度的绝对指标和相对指标，精度、准确度与精确度；理解测量不确定度。

第三章、协方差传播律及权（20分）理解数学期望的传播；掌握方差协方差阵、权、权阵、协因数、协因数阵的概念及其表示方法；掌握协方差传播律及其应用；熟练掌握权与定权的常用方法，协因数、协因数传播律及其应用，理解由观测值函数的真误差估计中误差的方法；了解系统误差的传播。

第四章、平差数学模型与最小二乘原理（10分）掌握各种平差问题必要观测数，多余观测数的确定方法；掌握测量平差的函数模型，函数模型的线性化，掌握参数估计与最小二乘平差准则。

第五章、条件平差（20分）熟练掌握条件数的确定，条件平差原理；掌握各种平差问题条件方程的建立；掌握法方程的组成与解算，精度评定。

第六章、附有参数的条件平差（15分）了解附有参数的条件平差函数模型和随机模型的建立；掌握法方程的组成与解算，精度评定。

第七章、间接平差（20分）掌握间接平差原理，误差方程的建立；掌握法方程的组成与解算，精度评定；掌握间接平差应用（直接平差，三角网坐标平差，导线网间接平差，GPS 网平差）。

第八章、附有限制条件的间接平差（15分）掌握附有限制条件的间接平差原理；掌握误差方程、条件方程列立；掌握法方程的组成与解算，精度评定。

第九章、概括平差函数模型（10分）熟悉基本平差方法的概括函数模型；附有限制条件的条件平差原理，精度评定；熟悉各种平差方法的共性与特征；理解平差结果的统计性质。

第十章、误差椭圆（10分）了解点位中误差概念以及计算方法；掌握任意方向的位差计算；点位误差的极大值和极小值的计算；理解误差曲线的基本概念；掌握误差椭圆要素计算；理解点位落入误差椭圆内的概率；第十一章、平差系统的统计假设检验（10分）熟悉统计假设检验的基本方法；了解误差分布的假设检验；掌握平差模型正确性的统计检验；理解平差参数的统计检验和区间估计；了解粗差检验的数据探测法。

误差理论与测量平差基础CH03

误差理论与测量平差基础CH03

误差理论与测量平差基础 第三章 协防差传播律及权 3-1 协防差传播律
2、多个观测值线性函数的方差阵
t×1
Z 和 Y 为多个观测值线性函数：
r×1 t ×1
Z = K X + K0
t×nn×1
t×1
r ×1
Y = F X + F0
r×nn×1
r×1
数学期望分别为： E (Z ) = K µ X + K 0
1×1
Z = f ( X ) = f ([X1 , X2 , · · · , Xn ]T )
n×1
在近似值X 0 按泰勒(台劳)级数展开(乎略二次以上项)
1×1
Z = k1 X1 + k2 X2 + · · · + kn Xn + k0 = K X + k0
1×nn×1
1×1
∂f ki = ( ∂ Xi )0
20
0 1 0.8 0.6 C 0.4 0.2 0
误差理论与测量平差基础 第三章 协防差传播律及权 3-2 协防差传播律的应用
三、若干独立误差的联合影响
一个观测结果同时受到许多独立误差的联合影响，如测角受 到照准、读数、目标偏心仪器偏心等误差的影响，观测结果真误 差是各独立误差的代数和 ∆Z = ∆1 + ∆2 + · · · + ∆n 它们的方差之间的关系为
2 2 2 2 σZ = σ1 + σ2 + · · · + σn
2 DZZ = σZ = KDXX K = K 2 DXX
变成上一章中所讲的方差的运算规则。
误差理论与测量平差基础 第三章 协防差传播律及权 3-1 协防差传播律
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
f f f dZ X dX 1 X dX 2 X dX n KdX 1 0 2 0 n 0
因此只要对非线性函数求全微分，获得系数矩阵即 可应用协方差传播率
第三章 协方差传播率及权
第三章 协方差传播率及权
令
dZ1 dX1 dZ2 dX 2 dZ , dX , dZ dX t n f1 X 1 f 2 K X 1 f t X 1 f1 X 2 f 2 X 2 f t X 2 f1 X n f 2 X n f t X n
则其方差——协方差矩阵定义为：
第三章 协方差传播率及权
DLL E L E ( L) L E ( L)
nn

T

式中： T E(L) E(l1 ) E(l2 ) E(ln ) 为观测向量的期望； l2 D(li ) E(li E(li ))2 为第i组观测值的方差；
作为衡量精度的指标，中误差可衡量一组观测值的 精度。在实际工作中，我们得到的观测值往往是由多 组观测值所构成的观测向量。比如，在GPS测量中， 基线观测值 L (x y z)T 就是观测向量。 衡量观测向量之精度的指标是方差—协方差矩阵。 一般地，设n维观测向量为
n1
L (l1 l 2 l n ) T
D XX


观测向量线性函数为
T D XX 2 2n n
12 1n 2 2 2n
Z KX k0
式中： K k1 k2 kn , k 0 为常数。
第三章 协方差传播率及权
Z的期望为
E(Z ) E( KX k0 ) KE ( X ) k0
0 1
0 2
0 n



f f 0 0 X n X n 二次以上项 X 2 X 2 X X 2 0 n 0




当X与X0非常接近时，可以略去二次以上小项（影响非常小） 微分以后的系数均为具体数值，将常数提取出来，即得：
Z k1 X1 k2 X 2 kn X n k0
第三章 协方差传播率及权
如果令：
dXi X i X i0
i 1,2,, n
T
dX dX1 dX2 dXn
0 0 dZ Z Z 0 Z f X10 , X 2 ,, X n


也可写为：
6、多个观测向量非线性函数的方差—协方差矩阵
基本思想：a、利用泰勒级数展开，略去二次以上项， 得到函数的线性表达式；b、应用协方差传播律。 设观测向量的t个非线性函数为：
Z1 f1 X 1 , X 2 , , X n Z t f t X 1 , X 2 , , X n Z 2 f 2 X 1 , X 2 , , X n
E( X 1 X 2 X n ) E( X 1 ) E( X 2 ) E( X n )
当随机变量 X 1 , X 2 ,, X n 两两独立时，有
E( X 1 X 2 X n ) E( X 1 ) E( X 2 )E( X n )
X、Y相互独立时：
E( X , Y ) E( X ) E(Y )
Z的方差为
DZZ E[(Z E ( Z ))(Z E ( Z ))T ] E[(KX k0 KE ( X ) k0 )(KX k0 KE ( X ) k0 )T ] KE[( X E ( X ))(X E ( EX ))T ]K T KDXX K T
同理：
T DZY KD XX F T DYZ t r
教材：例 3－4，3－5，P30上角例题
习题：3.2.14
第三章 协方差传播率及权
5、观测向量非线性函数的方差—协方差矩阵
设观测向量 X 的非线性函数为：
n1
Z f X1 , X 2 , , X n
已知X的协方差矩阵DXX，求函数Z的方差DZZ
i
i j
l2l1 lnl1
2 l1
l l l2 l l
12
2

n 2
l1ln l 2l n 2 ln
T
l2l E (li E (li ))(l j E (l j )) 为第i组观测值关于第j组观
第三章 协方差传播率及权
于是，观测向量的多个线性函数可写为 Z KX K 0 故有 DZZ KD XX K T
T 式中：DZZ DZZ为对称方阵。 若还有观测向量的另外r个线性函数 Y1 f11 X 1 f12 X 2 f1n X n f10 Y2 f 21 X 1 f 22 X 2 f 2 n X n f 20 Yr f r1 X 1 f r 2 X 2 f rn X n f r 0 其矩阵形式为： Y FX F0
则令
Z1 k11 Z2 k 21 Z , K t 1 t n Z k t t1 k12 k1n k10 k 22 k 2 n k 20 0 , K1 t k k t 2 k tn t0
第三章 协方差传播率及权
则有：
而
r t
T DYY FDXX F T DYY r r
DYZ E[(Y E (Y ))(Z E ( Z ))T ] E[(FX F0 FE( X ) F0 )(KX k 0 KE ( X ) k 0 ) T ] FE[( X E ( X ))(X E ( EX ))T ]K T FDXX K T
1 Qii pi
2 i 2 0
2 1 j Q jj 2 pj 0
ij Qij 2 0
1 PXX QX第三章 协方差传播率及权
设观测向量的t个非线性函数为：
Z1 f1 X 1 , X 2 , , X n Z t f t X 1 , X 2 , , X n
Z 2 f 2 X 1 , X 2 , , X n
第三章 协方差传播率及权
对上式求全微分，得
f f f dZ1 1 dX1 1 dX 2 1 X X X 1 2 n f f 2 f dX1 2 dX 2 2 dZ2 X X X 1 2 n f f f dZt t dX1 t dX 2 t X X X 1 2 n dX n dX n dX n
第三章 协方差传播率及权
§3-4 权与定权的常用方法
权的概念
表达观测值方差之间比例关系的数字特征 观测值所占的比重，精度越高，比重越大，即与方差大小成反比。
02 pi 2 i
权的定义
权的意义，不在于其数值的大小，重要的是它们之间的比例关系。
单位权中误差的概念
权为1的观测值所对应的中误差，称为单位权中误差。
第三章 协方差传播率及权
3、观测向量线性函数的方差
设观测向量X及其期望和方差为：
X ( X1 X 2 X n )T , E( X ) ( E( X 1 ) E( X 2 ) E( X n ))T
12 12 T E ( X E ( X ))(X E ( X )) 1n
第三章 协方差传播率及权
对上式求全微分，得
f f1 f dX1 1 dX 2 1 dZ1 X X X 1 2 n f 2 f 2 f 2 dZ2 X dX1 X dX 2 X 1 2 n f f t f dX1 t dX 2 t dZt X X X 1 2 n dX n dX n dX n
第三章 协方差传播率及权
第三章 协方差传播律及权
§3-1 观测向量及其方差—协方差矩阵
§3-2 协方差传播率
§3-3 协方差传播律的应用 §3-4 权与定权的常用方法 §3-5 协因数和协因数传律 §3-6 由真误差计算中误差及其实际应用
§3-7 系统误差的传播
第三章 协方差传播率及权
§3-1 观测向量及其方差—协方差矩阵
则由误差传播定律得：
DZZ KD XX K T
由以上推导知，求非线性函数的方差——协方差矩阵 比求线性函数的方差——协方差矩阵只多一个求全微 分的步骤。 教材：例 3－6、3－7 ， P33上角例题
习题：3.2.07(2)，3.2.11(2)，3.2.13
第三章 协方差传播率及权
§3-3 协方差传播率的应用
测值的协方差，协方差用来描述第i个观测值与第j个观 测值之间的相关程度。
第三章 协方差传播率及权
§3-2 协方差传播率
1、协方差传播律的作用 （图3－1示例）
计算观测向量函数的方差—协方差矩阵，从而评定观 测向量函数的精度。
2、预备公式
E(C) C , E(CX ) CE( X ) , E( X Y ) E( X ) E(Y )
定权的常用方法
1、水准测量的权 2、同精度观测值之算术平均值的权
教材：例 3－8，3－9 习题：3.4.35， 3.4.40， 3.4.41， 3.4.43， 3.4.44
第三章 协方差传播率及权