当前位置：文档之家 › §4圆轴扭转横截面上的应力

§4圆轴扭转横截面上的应力

  • 格式：ppt
  • 大小：901.00 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

材料力学 第四章 扭转

材料力学 第四章 扭转
W = Me 2 n
60 外力偶每秒所做的功即为输入的功率
P 1000= Me 2 n
60
明德行远 交通天下
材料力学
P─kW
M e 9549
P n
n─r/min
M e ─N m
或
P─PS(马力）
Me
7024
P
n
n─r/min M e ─N m
明德行远 交通天下
材料力学
二、扭矩及扭矩图
D
2 d
2
2
2
d
32
(D4
d
4)
D4 (1 4 ) 0.1D4 (1 4 )
32
d
( Dd )
O
D
明德行远 交通天下
材料力学
④ 应力分布
（实心截面）
（空心截面）
工程上采用空心截面构件：提高强度，节约材料，重量轻，
结构轻便，应用广泛。
明德行远 交通天下
材料力学
⑤ 确定最大剪应力：
由
Ip—极惯性矩，纯几何量，无物理意义。
Ip A 2dA
单位：mm4，m4。
③ 尽管由实心圆截面杆推出，但同样适用于空心圆截面杆，只是Ip值不同。
明德行远 交通天下
材料力学
对实心圆截面：
D
I p A 2dA
2 2 2 d
0
D4 0.1D4
32
d
O
D
对于空心圆截面：
d
I p A 2dA
A
B
M1 =9.55 103
P1 n
9.55
103
500 300
N
m=15.9kN
m
M 2 =M3 =9.55103

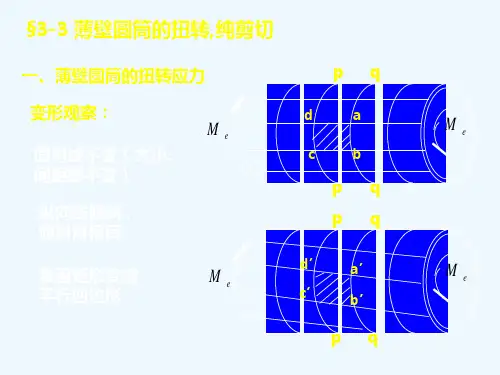
材料力学(第五版)扭转切应力

材料力学(第五版)扭转切应力

p
q
a’ b’
φ 圆轴两端面的
相对扭转角
M
d’
e
M
φ q R
e
c’
qq平面相对于pp的相对扭转 角为： d 圆轴表面的切应变γ 为：
p p
q
d c
p
a a
Rd a a d R ad dx dx
ρ
b
q
d R (a ) dx
b
现研究圆轴内部的切应变

圆轴内部的切应变
作 业
3-1
3-2
3-7
3-8
d G (c ) dx
0
0
d maxGR dx
R
三、静力关系
M
e
T dA ) (
A
T
代入: 得:
d G ( c ) dx
d 2 T G dA dx A
dA
令: 得:
IP dA
D
1
max
D2
扭转时切应力沿半径线性分布，圆心部分的 材料未能充分发挥作用。
例题
已知： P1=14kW,
P2= P3= P1/2=7 kW
n1= n2= 120r/min, z1=36, z3=12; d1=70mm, d 2 =50mm, d3=35mm
求:各轴横截面上的最大切应力。
P1=14kW， P2= P3=7 kW n1= n2= 120r/min
p
q
a’ b’
M
d’
e
M
e
c’
p
q
因为各圆周线大小、形状、间距都不变
2、沿同一圆周线上的切应力 大小相等

扭转—扭转轴的应力及强度计算(建筑力学)

扭转—扭转轴的应力及强度计算(建筑力学)
1.5 10 6


MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同，故两轴的最
大切应力相等，即
'max max 51.4MPa

max
Tmax
Tmax


WP
D23 1 4 16


6
16Tmax
16
变形的能力。单位GPa，其数值可由试验测得。
切应变的其单位是 弧度（rad）
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明，圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象，对圆轴内部的变形可做如下假设：扭转
截面（危险截面） 边缘点处。因此，强度条件也可写成 maxFra bibliotekTmax

[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题，即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴，承受的最大扭矩Tmax=1.5kN•m，轴
的直径d1=53mm。求：（1）该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成，扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下，发生扭转变形，直至破坏。
Q35钢
铸铁

轴的扭转-应力,强度

轴的扭转-应力,强度

T
T Ip
式中 T——所求切应力点的横截面 上的扭矩
B
B' dA

R O
max

——所求切应力点到圆心的距离
Ip=A2dA——横截面对圆心O的极惯性矩
注意：切应力公式的适用范围：max ≤p
3.最大切应力
T
max
即
TR Ip
B
B' dA

R O
T max Wp
´
上述公式可得到如下结论。
0
0
0 0 , 0 max
45 min , 45 0
45 max , 45 0
450
450 0 90
90 0 , 90 max
取 d = 29.7 mm。
可见：此轴的直径是由刚度条件控制的
155 N . m
圆轴扭转斜面上的应力
为什么研究斜截面应力？ ☆ ☆ 逻辑上，正截面——斜截面 实际上，见下面的实验结果，原因？
扭转轴的破坏（想一想：为什么这样？）
途径：1、仿正截面过程；2、用正截面推导斜截面应力
《应力状态理论》对于
2.应力公式推导 (1) 变形几何方面 取微段dx研究
Me
p
q
Me

x A p dx
T p

B q
O

x
d (1) tg dx d ——单位长度扭转角 式中 dx
即：
q R O2 B' d B C' C q dx
T

A
O1 A'

对给定的截面，与成正比

第四章杆件横截面上的剪应力(材料力学课件)

第四章杆件横截面上的剪应力(材料力学课件)



T h b2
T G hb3
1 max
表 5-1 矩形截面杆扭转时的系数
h/b 1.0 1.2 1.5 2.0 2.5 3.0 4.0 6.0 8.0 10.0 ∞ α 0.208 0.219 0.231 0.246 0.258 0.267 0.282 0.299 0.307 0.313 0.333 β 0.141 0.166 0.196 0.229 0.249 0.263 0.281 0.299 0.307 0.313 0.333 γ 1.000 0.930 0.858 0.796 0.767 0.753 0.745 0.743 0.743 0.743 0.743
N ─ kW

n
─
rpm
m ─ N m
N ─ PS

n
─
rpm
m ─ N m
{m}Nm

9549 {N}kW {n} r / min
{m}Nm

7024 {N}PS {n} r / min
GB3101-93中规定的数值方程式表示方法
扭矩和扭矩图:
例： 图示传动轴，主动轮A输入功率 NA=50 马力，从动轮B、C、D输出功率分 别为 NB=NC=15马力 ，ND=20马力，轴的 转速为n=300转/分。作轴的扭矩图。
剪切胡克定律:


CL5TU8
薄壁圆筒的实验, 证实了剪应力与剪应变之间 存在着象拉压胡克定律类似的关系, 即当剪应力 不超过材料的剪切比例极限τp时,剪应力与剪应 变成正比
G
G称为材料的剪切弹性模量。上式关系称为剪切 胡克定律
剪切弹性模量G 材料常数：拉压弹性模量E

第 4 章 圆轴扭转时的强度与刚度计算

第 4 章 圆轴扭转时的强度与刚度计算

基础篇之四第4章 圆轴扭转时的强度与刚度计算杆的两端承受大小相等、方向相反、作用平面垂直于杆件轴线的两个力偶，杆的任意两横截面将绕轴线相对转动，这种受力与变形形式称为扭转（torsion ）。

本章主要分析圆轴扭转时横截面上的剪应力以及两相邻横截面的相对扭转角，同时介绍圆轴扭转时的强度与刚度设计方法。

4－1 外加扭力矩、扭矩与扭矩图作用于构件的外扭矩与机器的转速、功率有关。

在传动轴计算中，通常给出传动功率P 和转递n ，则传动轴所受的外加扭力矩M e 可用下式计算：[][]e kw 9549[N m]r /min P M n =⋅其中P 为功率，单位为千瓦（kW ）；n 为轴的转速，单位为转/分（r/min ）。

如功率P 单位用马力（1马力=735.5 N •m/s ），则e []7024[N m][r /min]P M n =⋅马力 外加扭力矩M e 确定后，应用截面法可以确定横截面上的内力—扭矩，圆轴两端受外加扭力矩M e 作用时，横截面上将产生分布剪应力，这些剪应力将组成对横截面中心的合力矩,称为扭矩（twist moment ），用M x 表示。

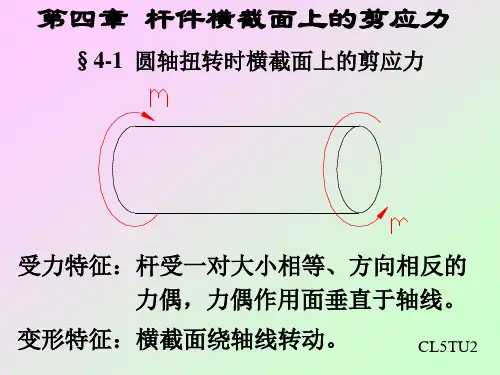
图4－1 受扭转的圆轴用假想截面m －m 将圆轴截成Ⅰ、Ⅱ两部分，考虑其中任意部分的平衡，有M x －M e = 0由此得到图4－3 剪应力互等M x = M e与轴力正负号约定相似，圆轴上同一处两侧横截面上的扭矩必须具有相同的正负号。

因此约定为：按右手定则确定扭矩矢量，如果横截面上的扭矩矢量方向与截面的外法线方向一致，则扭矩为正；相反为负。

据此，图4－1b 和c 中的同一横截面上的扭矩均为正。

当圆轴上作用有多个外加集中力矩或分布力矩时，进行强度计算时需要知道何处扭矩最大，因而有必要用图形描述横截面上扭矩沿轴线的变化，这种图形称为扭矩图。

绘制扭矩图的方法与过程与轴力图类似，故不赘述。

【例题4－1】 变截面传动轴承受外加扭力矩作用，如图4－2a 所示。

材料力学 圆轴扭转内力、应力

材料力学 圆轴扭转内力、应力
dx GIP


T
IP
27
§ 3.4 圆轴扭转时横截面上的应力
Mechanic of Materials


T
Ip
—横截面上距圆心为处任一点切应力计算公式。
4. 公式讨论：
① 仅适用于各向同性、线 弹性材料，在小变形时的 等圆截面直杆。
τ

O
② 式中： —该点到圆心的距离。
T—横截面上的扭矩，由截面法通过外力偶矩求得。 IP—极惯性矩，纯几何量，无物理意义。
重点：扭转内力、应力。 难点：切应力互等定理的证明。 学时安排：2
Mechanic of Materials
第八讲内容目录 第三章 扭 转
§ 3.1 扭转的概念和实例和实例 § 3.2 外力偶的计算 扭矩与扭矩图 § 3.3 纯剪切 § 3.4 圆轴扭转时横截面上的应力
目录
§ 3.1 扭转的概念和实例
§3-4 圆轴扭转时横截面上的应力
约为80GPa。
剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三
个常数。对各向同性材料，这三个弹性常数之间存在下列关系：
G

E 2(1
)
22
Mechanic of Materials
§ 3.4 圆轴扭转时横截面上的应力
一、圆轴扭转时横截面上的应力公式推导思路 （一）几何方面：
扭转时，圆轴的表面 变形和薄壁圆筒表面变形 相似。实验现象：
M
A

9549
36 300
1146N.m
MB

MC

9549
11 300

350N.m
MD

9549

圆轴扭转横截面上的应力

圆轴扭转横截面上的应力
140 N.m，Ip= 3105 mm4，l = 2 m，G = 80 GPa，[] = 0.5 ()/m 。AC=? ，校核轴的刚度。
解：1. 变形分析
T1 MA 180 N m

AB

T1l GIp

1.5010-2
rad
T2 MC 140 N m
BC

T2l GIp
例 5-1 已知 T=1.5 kN . m，[ ] = 50 MPa，试根据强度条 件设计实心圆轴与 = 0.9 的空心圆轴，并进行比较。
解：1. 确定实心圆轴直径
max [ ]
max

T Wp

T πd 3
16
T πd
3

[
]
16
d
3

16T
π[ ]
3

16(1.5103Nm) π(50106Pa)
3. 计算支座约束力偶矩
联立求解方程 (a) 与 (b)
MA

Mb ， ab
MB

Ma ab
总结
• 圆轴扭转强度计算 • 圆轴扭转刚度计算
本章结束！

0.0535
m
取： d 54 mm
2. 确定空心圆轴内、外径
Wp

πdo3 16
14
16T [ ]
π 16
do3
(1

4)
do

3
16T
π(1 4)[
]

76.3
mm
di do 68.7mm
取：do 76 mm， di 68 mm 3. 重量比较

工程力学-圆轴扭转变形分析

工程力学-圆轴扭转变形分析

P=7.5kW,轴的转速n=80r/min。试选择实心圆轴的直径d和空心圆轴的外
径d 2。己知空心圆轴的内外径之比=d 1/d 2=0.8,许用扭转切应力 [τ]=40MPa。
解：（1）外力偶矩为
M e 9550 7.5 N m 895 .3 N m 80
（2）扭矩为 T = Me = 895.3N· m （3）实心圆轴直径 根据强度条件
各点切应力的大小与该点到圆心的距离成正比，其分布 规律如图
圆轴扭转时，最大切应力 max 发生在圆轴表面。当ρ=R 时，其值为：
TR T max Ip IP / R
令 Wp
Ip R
max
T Wp
Wp称为扭转截面系数，它表示截面抵抗扭转破坏的能 力，单位是（mm）3。
工程中承受扭转的圆轴通常采用实心圆轴和空心圆轴两种形
max
T 16T 3 Wp πd
16 T 3 16 895.3 d 3 m 0.048m 48mm 6 [ ] 3.14 40 10
（4）空心圆轴外径
根据强度条件
max
T 16T 3 4 Wp πd 2 (1 )
16 T 16 895.3 3 d2 m 4 6 4 [ ](1 ) 3.14 40 10 (1 0.8 )
3
0.058m 58m m
内径d 1=α×d 2= 0.8×58 mm = 46.4mm
（5）比较重量
在长度相等、材料相同的情况下，空心圆轴与实心圆 轴重量之比等于横截面面积之比，即
四、圆轴扭转时的强度 计算
圆轴的扭转的强度条件
max
Tmax Wp

园轴扭转横截面上剪应力计算

园轴扭转横截面上剪应力计算

于是单元体abcd的ab边相对于cd也发生了微小的相对错 动，引起单元体abcd的剪切变形。
如图所示：ab边对cd 边相对错动的距离是：
m
n aa' Rd
d c
a
a
b
eR e
d
b
m
n
dx
e
e d
m
n
d c
a
a
b
eR e
d
b
m
n
dx
aa' R d 直角abc的角度改变量： ad dx
e
§4-1 扭转的概念
一、引例 F
F
M 二、概念
作用于杆件上的外力，为两个大小相等、方向相反、且作 用平面垂直于杆件轴线的力偶时，杆件中任意两个横截面即会 发生绕杆件轴线相对转动，这种形式的变形就称为扭转变形。
目录
• 受扭转构件的受力特点
——在垂直于杆轴的两平面内分别作用两个 等值，反向的力偶。 m m
处作用有载荷P。求：C点水平及铅垂位移
B
解：
a
A
C
aP a
C/
复习
§4-1 扭转的概念
1 扭转 2 轴
§4-2 外力偶矩的计算 扭矩和扭矩图
1 两个公式
2 扭矩的正负规定
§4-3 薄壁圆筒扭转时的应力 剪切虎克定律 1 应力计算方法和公式 2 剪切虎克定律公式 3 E G μ之间的关系
§4-4 圆轴扭转时的应力和强度条件
e d
—（a）
——圆截面a点处的剪应变，在垂直于半径oa的平面内。
同样道理：在距离圆心为处的剪应变为：
p
d
dx
—（b）
讨论：由图中可看出：（a）(b)两式中的

理论力学第四章扭转

理论力学第四章扭转
由 M x 0, T Me 0 得T＝M e
内力T称为截面n-n上的扭矩。
Me
Me
x T
Me
扭矩的符号规定：按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向，大拇指代表其矢量方向，若 其矢量方向与截面的外法线方向相同，则扭矩规定为正值，反之为 负值。
+
T
-
扭矩图：表示沿杆件轴线各横截面上扭矩变化规律的图线。
4
32 7640180 80109 π 2 1
86.4 103 m 86.4mm
d1 86.4mm
4.直径d2的选取
按强度条件
A M e1 d1
B d2 C
M e2
M e3
3 16T 3 16 4580
②各纵向线均倾斜了同一微小角度 。
③所有矩形网格均歪斜成同样大小的平行四边形。
结论：
0, 0
横截面上
0 0
根据对称性可知切应力沿圆周均匀分布；
t D, 可认为切应力沿壁厚均匀分布, 且方向垂直于其半径方向。
t
D
微小矩形单元体如图所示：
①无正应力
②横截面上各点处，只产生垂 直于半径的均匀分布的剪应力
强度计算三方面：
① ②
校核强度：
max
Tm a x WP
设计截面尺寸：
WP
Tmax
[ ]
[ ]
Wt
实：D3 16 空：1D6（3 1 4）
③ 计算许可载荷： Tmax WP[ ]
例4.2 图示阶梯状圆轴，AB段直径 d1=120mm，BC段直径
d2=100mm 。扭转力偶矩 MA=22 kN•m， MB=36 kN•m， MC=14 kN•m。 材料的许用切应力[t ] = 80MPa ，试校核该轴 的强度。

讨论圆轴扭转时的应力状态

讨论圆轴扭转时的应力状态

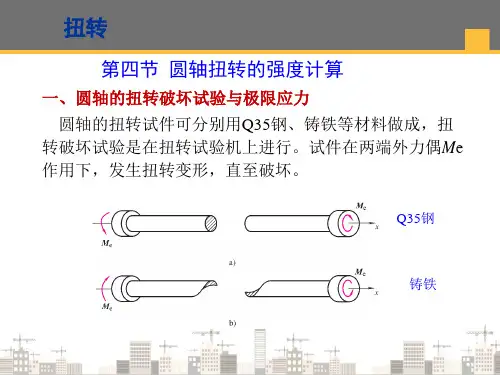
130一、讨论圆轴扭转时的应力状态，并分析铸铁试件受扭时的破坏现象。

解 根据第十九章讨论，圆轴扭转时，在横截面的边缘处剪应力最大，其数值为:n n W M=τ (e )在圆轴的最外层，按图22-5(a )，所示方式取出单元体ABCD ，单元体各面上的应力如图22-5(b )所示。

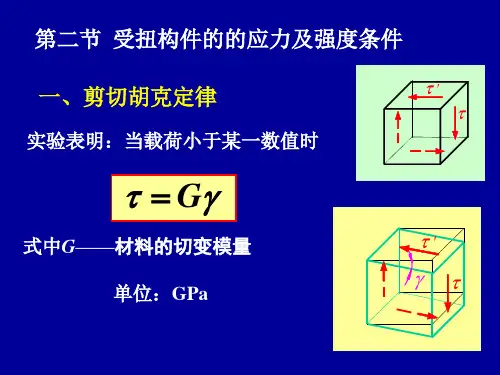
在这种情况下，ττσσ===xy y x ，0 （f ）单元体侧面上只有剪应力作用，而无正应力作用的这种应力状态称为纯剪切应力状态。

把(f )式代入公式(22-6)得:min maxσσ ττσσσσ±=+-±+=22)2(2xy y x y x 由公式（22-5）：yx xytg σστα--=220 →∞-所以 2709020--=或α450-=α 或 1350-=α以上结果表明，从x 轴量起，由 450-=α(顺时针方向)所确定的主平面上的主应力为max σ；而由 1350-=α所确定的主平面上的主应力为min σ。

按照主应力的记号规定：τσσστσσ-=====min 32max 10所以，纯剪切是二向应力状态，两个主应力的绝对值相等，都等于剪应力τ，但一个为拉应力，一个为压应力。

圆截面铸铁试件扭转时，表面各点max σ所在的主平面联成倾角为︒45的螺旋面[图22-5（a ）]。

由于铸铁抗拉强度较低，试件将沿这一螺旋面因拉伸而发生断裂破坏，如(a )(c ) 图22-5131图22-5（c ）所示。

二、 图22-6（a ）所示为一横力弯曲下的梁，求得截面m －n 上的弯矩M 及剪力Q 后，算出截面上一点A 处弯曲正应力和剪应力分别为：MPa MPa 50,70=-=τσ[图22-6（b ）]试确定A 点处的主应力及主平面的方位，并讨论同一横截面上其它点处的应力状态。

解 把从A 点处截取的单元体放大如图22-6（c ）所示。

选定x 轴的方向垂直向上，则0=x σ MPa y 70-=σ MPa xy 50-=τ由公式（22-5）得： 429.1)70(0)50(2220=----=--=yx xytg σστα︒=5520α或︒235 ︒=5.270α或︒5.117从x 轴量起，按逆时针方向量取的角度︒5.27，确定max σ所在主平面，以同一方向量取的角度,5.117︒确定min σ所在的另一主平面。

材料力学 (扭转)(四章 圆轴扭转时的强度与刚度计算)

材料力学 (扭转)(四章 圆轴扭转时的强度与刚度计算)

Mx 0: T1 MA 0
C
T1 MA 7.03KN.m
22
Mx 0: -T2 MC 0
T2 MC 2.32KN.m
X
(4)讨论现在的设计是否合理。
若将A轮与B轮调换， X 则扭矩图如下：
可见轴内的最大扭矩值减小了。10
T(KN.M)
§3.2 薄壁圆筒扭转
在圆筒表面画 上许多纵向线 与圆周线,形成 许多小方格.
G
剪切胡克定律
Ｇ－剪切弹性模量
G E
2(1 )
2021/8/19
17
圆轴扭转时的应力和变形
根据观察到的现象， 经过推理，得出关于圆 轴扭转的基本假设。
m
m
圆轴扭转变形前的横截面，变形后仍保持为平面，
形状和大小不变。且相邻两截面间的距离不变。这就 是圆轴扭转的平面假设。
2021/8/19
18
二. 应力在横截面上的分布
2
而象电动机的主轴，水轮 机的主轴也承受扭转作用， 但这些零件除扭转变形外， 还伴随有其它形式的变形， 属于组合变形。
• 以扭转变形为主要变形形式的构件通常称为轴。 • 工程上应用最广的多为圆截面轴，即圆轴。
2021/8/19
3
• 扭转受力的特点是：
• 在构件的两端作用两个大小相等、方向相反且作 用面垂直于构件轴线的力偶矩。致使构件的任意 两个截面都发生绕构件轴线的相对转动，这种形 式的变形即为扭转变形。
在转矩m作用下，发现圆 周线相对地旋转了一个角 度，但大小、形状和相邻 两圆周线的距离不变。
表明，在圆筒的横截面上没有正应力和径向剪应力。
2021/8/19
11
设圆筒平均半径为r，筒壁厚度为t
因圆筒壁厚很小，可认为剪应力沿

圆截面轴的扭转应力与变形

圆截面轴的扭转应力与变形

对应拉压问题 与轴力图
q
F 3ql
l
l/2 l/2
FN ql
x
2ql
Page 7
第四章 扭转
3. 轴的动力传递
已知传动构件的转速与所传递的 功率，计算轴所承受的扭力矩。
电机
联轴器
A
B
P M
角速度 2 n
60
n : 转速 (r min) 功率：KW 力偶矩：N.m
P 103 M 2 n
60
T1 ( x)
ml
2ml
在AB、BC和CD段分别由三截面 x 切开，考察左（或右）段平衡
D
AB段： T1 x mx
BC段： T2 ml
CD段： T3 2ml
画扭矩图
x
•试与轴力图比较，
考察对应关系。
Page 6
2.扭矩图对应的轴力图
M 3ml
m
A
B
C
D
l
l/2 l/2
T ml
x
2ml
第四章 扭转
R1
R2
O
T
空心轴
O
T
IP
空心圆能用？
思考:同样横截面积S的实心圆与空心圆,哪个强度性能好
实心圆 S D02
4
D 4S
空心圆
D2(12 )
S
4
4S D
12
Page23
实心圆 空心圆
D0
4S
D
4S
1 2
实心圆
Wp
D03
16
S
空心圆 Wp
4 D0
Wp S (1 2 )D
4
第四章 扭转
三、圆轴合理截面与减缓应力集中

工程力学第4节 圆轴扭转时横截面上的应力

工程力学第4节 圆轴扭转时横截面上的应力
解：1）计算外力偶矩
P T M A 9550 742 N m n T 74210103 Pa 5.84 MP 4 IP D 32 T T 742 max Pa 17.5 MP 3 3 WP D 0.060 16 16
平面截面假设：圆轴扭转变形后，横截面仍保持为 平面，且其形状大小不变，横截面上的半径仍保持 为直线，即横截面刚性地绕轴线作相对转动。
圆轴扭转时横截面上 的应力关系
d AA tan R KA dx
K
A A'
L
B B'
BB d tan LB dx
一、扭转切应力的一般公式 1、变形的几何关系 试验观测：取一易变形的 圆形截面直杆，在此圆轴 的表面各画几条相平行的 圆周线和纵向线；在轴的 两端施加一对力偶矩 M 使 其产生扭转变形。
观测结果
1）圆周线的形状和大小不变，两相邻圆周线的间距 保持不变，仅绕轴线作相对转动。
2）纵向线均倾斜了一个角度 。
D
d
空心圆截面 令内外径比为 =d/D，则有：
I p d / 2 2 d 4 D 4 (1 ) 32
D/2 2
D3 WP (1 4 )
16
例7-3 已知实心轴的直径 D 60 mm，轴的转速 n 450 r/min，传递的功率 P 35 kW，试求：距圆 心为 10 mm处的切应力，以及最大切应力。
等直圆轴扭转时横截面上 任一点处切应力的计算公式
max
TR IP
max
I P / R 称为抗扭截面模数
T WP
三、圆截面极惯性矩 及抗扭截面模数 实心A dA 2 d 3 d 4 D WP 32 16
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空心截面比 实心截面好
2. 采用变截面轴与阶梯形轴
若Ro/d 过大
将产生皱褶
注意减缓 应力集中
17
例题
例 5-1 已知 T=1.5 kN .m，[ ] = 50 MPa，试根据强度条 件设计实心圆轴与 = 0.9 的空心圆轴，并进行比较。
解：1. 确定实心圆轴直径
max[]
max
T Wp
T πd3
π4(do2 di2) πd2
39.5%
4
空心轴远比 实心轴轻
19
例 5-2 R0＝50 mm的薄壁圆管，左、右段的壁厚分别
为 d1 5 mm，d2 4 mm，m = 3500 N . m/m，l = 1 m， [] 50 MPa，试校核圆管强度。
解：1. 扭矩分析
20
2. 强度校核 危险截面：截面 A与 B
10
圆截面的 极惯性矩与抗扭截面系数
空心圆截面 d D
Ipπ3D2414
WpIDpπ1D63 14
2
11
圆截面的 极惯性矩与抗扭截面系数
实心圆截面 0
I
p
πd 4 32
Wp
πd 3 16
12
例题
例 4-1 已知MC= 2MA= 2MB=200N·m；AB段，d=20mm； BC段，di=15mm，do=25mm。求各段最大扭转切应力。
max[]
变截面或变扭矩圆轴:
max
T Wp
max
等截面圆轴:
max
Tmax Wp
[ ] u n
u－材料的扭转极限应力
n - 安全因数
危险点处于纯剪切状态，又有
塑性材料：[] =（0.5~0.577）[s] 脆性材料：[] = （0.8~1.0）[st]
16
圆轴合理截面
1. 合理截面形状
16
T πd
3
[
]
16
d
3
16T
π[ ]
31π(61(. 5 511030 60N Pm a))0.503m 5
取 ： d54mm
18
2. 确定空心圆轴内、外径
Wp
πdo3 14
16
16T [ ]
1π6do3(14)
do3π(11T 64)[]76.3mm di do6.87mm
取 d o ： 7m 6， m d i6m 8 m 3. 重量比较
满足刚度条件
27
例 6-2 试求图示轴两端的支座约束力偶矩（静不定问题）
解：1. 问题分析
M x 0 , M A M B M 0 (a)
未知力偶矩－2个，平衡方程－1个，一度静不定 需要建立补充方程，才能求解
28
M x 0 , M A M B M 0 (a)
2. 建立补充方程
A BA CC B 0
max[]
T
Ip
max
G[ ]
TmaxGpI[]
25
例题
例 6-1 已知：MA = 180 N.m， MB = 320 N.m， MC = 140 N.m，Ip= 3105 mm4，l = 2 m，G = 80 GPa，
[] = 0.5 ()/m 。AC=? ，校核轴的刚度。
解：1. 变形分析
T 1M A 18 N m 0
A
TA
2πR02d1
2πm R02d1l4.46MP [a]
ml
B
TB
2πR02d2
2πR202d227.9MPa[]
21
§6 圆轴扭转变形与刚度计算
圆轴扭转变形 圆轴扭转刚度条件 例题
22
圆轴扭转变形
扭转变形一般公式
d
dx
T GI
p
d T dx
GI p
T dx
l GI p
GIp－圆轴截面扭转刚度，简称扭转刚度
AC
T1a GI p
( M A)a GI p
CB
T2b GI p
M Bb GI p
提问
• 切应力互等定理 • 薄壁圆筒横截面上切应力公式 • 剪切胡克定律
1
§4 圆轴扭转横截面上的应力
扭转试验与假设 扭转应力分析 极惯性矩与抗扭截面系数 例题
2
扭转试验与假设
从试验、假设入手,综合考虑几何、物理与静力学三方面 试验现象一
各圆周线的形状不变,仅绕轴线作相对转动 当变形很小时，各圆周线的大小与间距均不改变
3
试验现象二
4
扭转平面假设 各横截面如同刚性平面，仅绕轴线作相对5转动
6
7
dx
d
a
b
a'
c
c'
b'
d
d'
d
dx
G
d
dx
AdAT
8
dx
d
a
b
a'
c
c'
b'
d
d'
T
Ip
Ip
2dA
A
－极惯性矩
9
T
Ip
max
TR T Ip Ip R
max
T Wp
Wp
Ip R
－抗扭截面系数
公式的适用范围：圆截面轴；max≤p
14
扭转失效与极限应力
扭转失效形式
塑性材料
屈服
断裂
脆性材料
断裂
扭转极限应力 圆轴扭转屈服时横截面上的最大切应力－扭转屈服应力 圆轴扭转断裂时横截面上的最大切应力－扭转强度极限
扭转屈服应力s ，扭转强度极限b －扭转极限应力u
15
圆轴扭转强度条件
为保证轴不因强度不够而破坏，要求轴内的 最大扭转切应力不得超过扭转许用切应力
dx
2
T2 GIp
因T1 T2
故d d T1
dxmaxdx1 GpI
d d x m (a 8 1 x 9 P 0 1 0N a 1 8 m 5 1 ) 0 0 - 1 ( m 0 4 2 ) 3 1 π 0 . 8 . 4 0 ( ) 0 / 3 m []
注意单位换算！
常扭矩等截面圆轴
Tl GI p
23
圆轴扭转刚度条件
ddx GTIp
T GIp
m
a
x
[
]
圆轴扭转刚度条件
[ ]－单位长度的许用扭转角
一般传动轴， [ ] = 0.5 ~1 ()/m
注意单位换算:
1ra/dm1π8(0)/m
24
圆轴扭转刚度条件 利用刚度条件可以进行三类计算：
① 校核刚度： ② 设计截面尺寸： ③ 计算许可载荷：
ABG T1lpI1.5010-2rad
T 2 M C 1N 4 m 0
BCG T2lpI1.1710-2rad
26
AC A BBC 1 1 .- 2 5 1 0 . 1 0 1 7 - 2 0 . 3 1 3 - 2 r 0 ad
2. 刚度校核
d T1
dx 1 GIp
d
解：
T1MA
W
p
πd 3 16
1, max
T1 Wp
T2MCΒιβλιοθήκη 2, maxT2 Wp
d i do
Wpπ1d6o3 14
1,max1π6M d3A 6.3 7MaP 2m , ax πd103(61MC 4) 7.4 9MaP 13
§5 圆轴扭转强度与合理设计
扭转失效与扭转极限应力 圆轴扭转强度条件 圆轴合理强度设计 例题