结构力学第3章 多跨静定梁课件
- 格式:ppt
- 大小:3.28 MB
- 文档页数:19


第三节多跨静定梁多跨静定梁是由若干根单跨静定梁(简支梁、悬臂梁和外伸梁)用铰相连,用来跨越几个相连跨度的静定结构。
多跨静定梁在公路桥梁和房屋结构中经常采用。
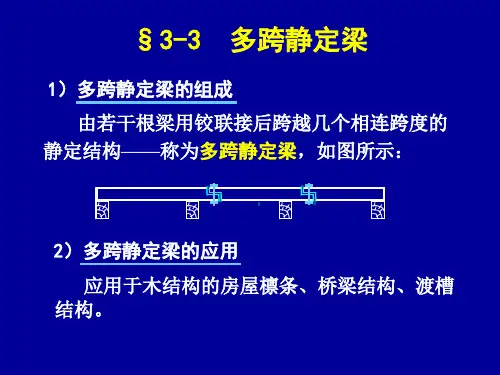
图3-13(a)为常见的屋架木檩条的构造简图,檩条支承在屋架的上弦上,支承处可简化为铰支座。
在檩条接头处采用斜搭接并用螺栓连接,这种结点可看作铰结点,因此它的计算简图如图3-13(b)所示。
它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁(图3-13(c))。
根据几何组成分析,确定其为无多余约束的几何不变体系,故称为多跨静定梁。
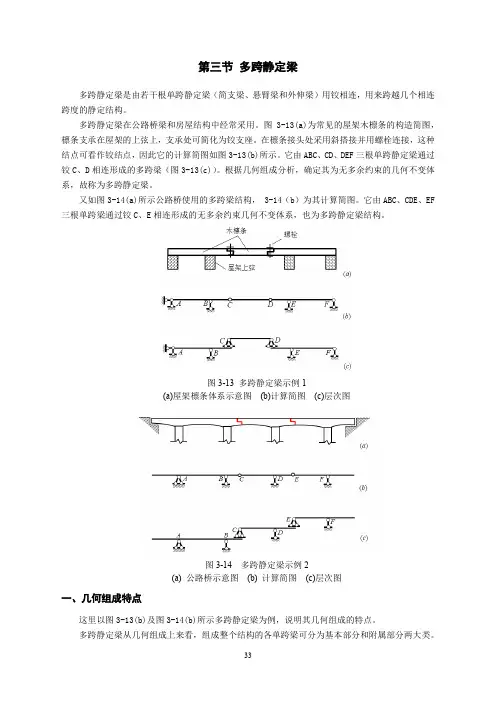
又如图3-14(a)所示公路桥使用的多跨梁结构, 3-14(b)为其计算简图。
它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系,也为多跨静定梁结构。
图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例,说明其几何组成的特点。
多跨静定梁从几何组成上来看,组成整个结构的各单跨梁可分为基本部分和附属部分两大类。
基本部分是指本身能独立维持平衡的部分,而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。
因此,多跨静定梁从几何组成上来看见,是先固定基本部分,再固定附属部分。
如图3-13(b)中多跨静定梁,梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础,它不依赖于其他部分就能独立维持自身的几何不变性;梁段DEF 虽然只有两根链杆与基础相连,但在竖向荷载作用下自身也能维持平衡。
因此,梁段ABC 、梁段DEF 均为基本部分。
而梁段CD 支承于前述两个基本部分上,它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变,所以是附属部分。
为了更清楚地表明多跨静定梁中各梁段之间的支承关系,常把基本部分画在附属部分的下方,附属部分画在基本部分的上方,如图3-13(c)所示,称为层次图。

第3章静定结构的内力计算§3-0 概述§3-1 多跨静定梁的计算§3-2 静定刚架的计算§3-3 三铰拱的计算§3-4 静定桁架的计算§3-5 组合结构的计算§3-6 静定结构的特性12§3-0 概述1 静定结构计算的基本原理——平衡∑X=0∑Y=0∑M=0取脱离体,列平衡方程计算内力,是计算静定结构的捷径,法宝。
当你不会计算静定结构内力的时候,当你冥思苦想的时候,请你取脱离体,正确答案就在前面。
静定结构的任一部分(脱离体)都满足静力平衡方程。
2 静定单跨梁的计算3 内力图几个通俗易懂的规律4 叠加原理1 静定结构计算的基本原理——平衡3内力符号的规定轴力—使杆件产生伸长变形为正,画轴力图要注明正负号。
剪力—使杆微段有顺时针方向转动趋势的为正,画剪力图要注明正负号。
弯矩—弯矩图画在杆件受拉一侧,不注符号。
MMNNQQ4m M 图有一尖点,荷载向下尖点也向下。
Q 图有一突变。
荷载向下, Q 图突变也向下(从左向右看)。
集中力矩作用点M 图有一突变。
荷载向下,M 图向下凸;Q 图为直线。
荷载向下,直线由左向右下斜2 静定单跨梁的计算(要求牢记)qP/2P/2Pl/4ql/28m/2m/25(m 2-m 1)/l注意:内力图阴影线代表了内力的大小!错误画法正确画法mm 1m 2PlPq ql212ql3 内力图几个通俗易懂的规律•1 荷载的指向就是弯矩图的凸向。
反之,弯矩图的凸向就是荷载的指向。
•2 结构有集中力,弯矩图就有尖点。
反之,如果弯矩图有尖点,则结构就有集中力。
•3 弯矩图在铰处的弯矩值一般为零(铰处一般没有弯矩)。
•4 荷载集度q=0,弯矩图为直线。
反之,如果弯矩图为直线,则荷载集度q=0。
•5 两个杆件相交的刚结点,当结点处无外力矩作用时,两根杆件的杆端弯矩大小相等,同为外侧受拉,或同为内侧受拉。
674叠加原理BM M BM BM M 2M=M 1+M 2M B弯矩图画法: (很重要! 贯穿结构力学始终)1.先画两端力矩产生的梯形弯矩图。