03静定梁--习题
- 格式:ppt
- 大小:1.88 MB
- 文档页数:31

第3章 静定梁与静定刚架
3.1 复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁 ★★★★
1.内力
表3-1-1 内力的基本概念
图3-1-1
图3-1-22.内力与外力间的微分关系及积分关系(1)由平衡条件导出的微分关系式
计算简图如图3-1-3所示,微分关系式为
(Ⅰ)
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-()()
图3-1-3
(2)荷载与内力之间的积分关系
如图3-1-4
所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-2。
图3-1-4
表3-1-2 内力的积分公式及几何意义
3.叠加法作弯矩图
表3-1-3 常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁 ★★★★
多跨静定梁是由构造单元(如简支梁、悬臂梁)多次搭接而成的几何不变体系,其计算简图见图3-1-7,几何构造、计算原则、传力关系见表3-1-4。


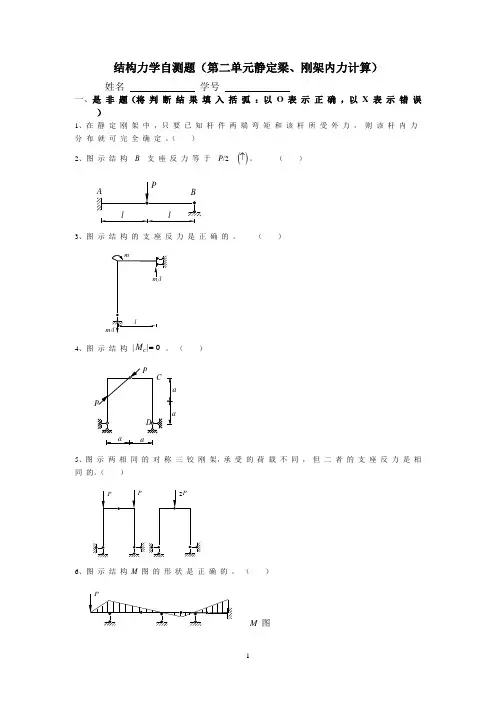
结构力学自测题(第二单元静定梁、刚架内力计算)姓名 学号一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )1、在 静 定 刚 架 中 ,只 要 已 知 杆 件 两 端 弯 矩 和 该 杆 所 受 外 力 , 则 该 杆 内 力 分 布 就 可 完 全 确 定 。
( )2、图 示 结 构 B 支 座 反 力 等 于 P /2 ()↑。
( )3、图 示 结 构 的 支 座 反 力 是 正 确 的 。
( )m 4、图 示 结 构 ||M C =0 。
( )a a5、图 示 两 相 同 的 对 称 三 铰 刚 架,承 受 的 荷 载 不 同 ,但 二 者 的 支 座 反 力 是 相 同 的。
( )6、图 示 结 构 M 图 的形 状 是 正 确 的 。
( )M 图二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )1、对 图 示 的 AB 段 , 采 用 叠 加 法 作 弯 矩 图 是 :A. 可 以 ;B. 在 一 定 条 件 下 可 以 ;C. 不 可 以 ;D. 在 一 定 条 件 下 不 可 以 。
( )2、图 示 两 结 构 及 其 受 载 状 态 , 它 们 的 内 力 符 合 。
A. 弯 矩 相 同 , 剪 力 不 同 ;B. 弯 矩 相 同 , 轴 力 不 同 ;C. 弯 矩 不 同 , 剪 力 相 同 ;D. 弯 矩 不 同 , 轴 力 不 同 。
( )P P ll l3、 图 示 结 构 M K ( 设 下 面 受 拉 为 正 ) 为 :A. qa 22 ; B -qa 22 ;C. 3qa 22 ;D. 2qa 2 。
( )2 a4、图示 结 构 M DC (设 下 侧 受 拉 为 正 )为 :A. - Pa ;B. Pa ;C. -Pa ;D. Pa 2。
()三、填 充 题 ( 将 答 案 写 在 空 格 内 )1、在 图 示 结 构 中, 无 论 跨 度,高 度 如 何 变 化,M CB 永 远 等 于 M BC 的 倍 ,q使 刚 架 侧 受 拉 。


第3章静定梁与静定刚架复习思考题1.用叠加法作弯矩图时,为什么是竖标的叠加,而不是图形的拼合?答:因为有时叠加弯矩图时的基线与杆轴不重合,如果用图形拼合,不能完全保证叠加后弯矩值是实际同一点的两个弯矩相加后的值。
2.为什么直杆上任一区段的弯矩图都可以用简支梁叠加法来作?其步骤如何?答:(1)因为根据内力分析可以求出直杆任一区段两端的内力,所以直杆任一区段两端均可以看成两端有外力(集中力或集中力偶)的简支梁。
(2)设有直杆任一区段简支梁AB,具体步骤如下①分解作用区段AB上的荷载;②分别作出分解荷载下的弯矩图;③求解出区段AB两端的弯矩M A和M B;④将两端弯矩M A和M B绘出并连以直线(虚线);⑤以步骤④中的虚线为基线叠加各个分解荷载下的弯矩图(竖标叠加),得最终弯矩图。
3.试判断图3-1所示刚架中截面A、B、C的弯矩受拉边和剪力、轴力的正负号。
图3-1答:轴力以受压为负,受拉为正;剪力以使截面顺时针旋转为正。
(1)截面A:左边受拉,剪力为负,轴力为负;(2)截面B:右边受拉,剪力为正,轴力为正;(3)截面C:左边受拉,剪力为正,轴力为正。
4.怎样根据静定结构的几何构造情况(与地基按两刚片、三刚片规则组成,或具有基本部分与附属部分等)来确定计算反力的顺序和方法?答:(1)与地基按两刚片,例如简支梁,支座反力只有三个,对某一端点取矩直接解除约束反力。
(2)与地基按三刚片规则组成,例如三铰刚架,支座反力有四个,考虑结构整体的三个平衡方程外,还需再取刚架的左半部(或右半部,一般取外荷载较少部分)为隔离体建立一个平衡方程方可求出全部反力。
(3)具有基本部分与附属部分时,按先附属后基本的计算顺序,求解支座反力。
5.当不求或少求反力而迅速作出弯矩图时,有哪些规律可以利用?答:当不求或少求反力而迅速作出弯矩图时,如下规律可以利用(1)结构上若有悬臂部分及简支梁部分(含两端铰接直杆承受横向荷载)弯矩图可先行绘制出;(2)直杆的无荷区段弯矩图为直线和铰处弯矩为零;(3)刚结点的力矩平衡条件;(4)外力与杆轴重合时不产生弯矩;(5)外力与杆轴平行及外力偶产生的弯矩为常数;(6)对称性的合理利用;(7)区段叠加法作弯矩图。


结构力学静定多跨梁例题一个结构力学静定多跨梁例题如下:假设有一根静定多跨梁,有三个等距的支点,梁长为L,弯矩载荷为M。
梁的截面形状为矩形,宽度为b,高度为h。
梁的材料为钢材,弹性模量为E。
求解该横梁在每个支点的支反力。
解题步骤如下:1. 画出梁的剪力图和弯矩图,在每个支点处标注支反力Ra、Rb和Rc。
2. 针对每个支点,应用力平衡条件,即对于任意截面处的受力情况进行分析。
a) 在支点A处,由于该支点不受水平力的作用,只有垂直支反力Ra。
根据力平衡条件,有:Ra = M/L。
b) 在支点B处,有垂直支反力Rb和水平支反力Hb。
由于该支点不受竖直力的作用,有:Rb = Ra + M/L,Hb = 0。
c) 在支点C处,有垂直支反力Rc和水平支反力Hc。
由于该支点不受竖直力的作用,有:Rc = Rb + M/L,Hc = 0。
3. 再应用弯矩平衡条件,根据剪力图和弯矩图的关系求解支反力。
a) 在悬臂端A处,由于支反力Ra是唯一的垂直力,可以得到弯矩方程:Ma = -M。
b) 在支点B处,可以得到弯矩方程:Ma + Mb = 0,即-M + Rb*(L/2) = 0。
c) 在支点C处,可以得到弯矩方程:Ma + Mb + Mc = 0,即-M + Rb*(L/2) + Rc*L = 0。
4. 将以上三个方程联立求解,即可得到支反力Ra、Rb和Rc的具体数值。
需要注意的是,在实际求解过程中,可能还需要考虑其他因素,如材料的应力和变形等。
此处只给出了一个简化的静定多跨梁的例题。
真实的工程问题可能更为复杂,需要综合考虑不同因素进行分析和计算。

结构力学静定多跨梁例题
静定多跨梁是结构力学中的经典问题之一,它涉及到梁的静力
学分析和梁的内力计算。
静定多跨梁例题通常包括确定多跨梁的支
座反力、梁的内力分布以及梁的变形等内容。
首先,我们需要明确多跨梁的几何形状、材料特性和受力情况。
假设我们有一跨数大于等于3的多跨梁,每个支座处有竖向力和弯
矩作用,梁的自重也需要考虑在内。
在解题过程中,我们通常采用
梁的受力平衡方程和变形方程来进行分析。
通过这些方程,我们可
以求解出支座反力、梁的内力分布和梁的变形情况。
其次,针对静定多跨梁的例题,我们可以采用不同的方法进行
求解,比如方法一般有,图解法、力法、位移法等。
在实际应用中,我们可以根据具体情况选择最合适的方法进行分析。
在解题过程中,我们需要考虑梁的受力特点,比如悬臂梁、悬
臂梁等不同类型的受力情况。
同时,还需要考虑梁的材料特性,比
如弹性模量、截面形状和尺寸等因素对梁的受力性能的影响。
此外,静定多跨梁的例题还涉及到梁的内力分布,包括弯矩和
剪力的计算。
这需要我们对梁的受力特点有深入的理解,同时也需要灵活运用力学知识进行分析。
总之,静定多跨梁的例题是结构力学中重要的内容,通过深入分析和综合运用力学知识,我们可以解决这类问题并且加深对结构力学原理的理解。
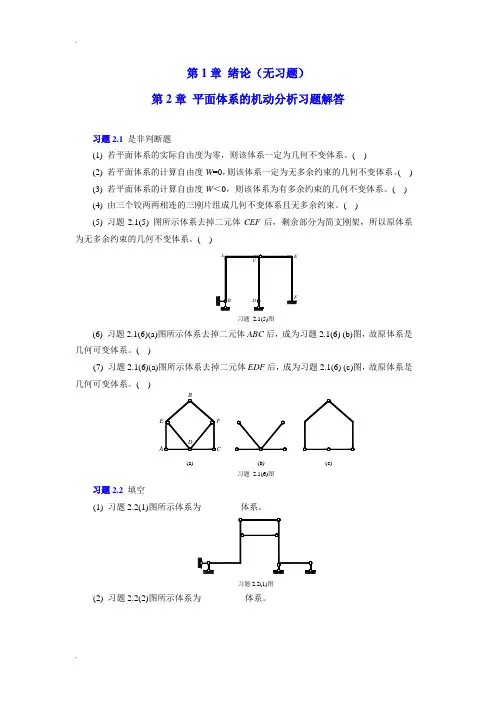

第三章静定结构受力分析3.1判断题,并说明原因。
1.静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
()原因:2.静定结构受外界因素影响均产生内力。
大小与杆件截面尺寸无关。
()原因:3.静定结构的几何特征是几何不变体系。
()原因:4.静定结构在支座移动时,会产生变形。
()原因:5.两个弯矩图的叠加不是指图形的简单拼合,而是指两图对应的弯矩纵矩叠加。
()原因:6.在相同的荷载和跨度下,静定多跨梁的弯距比一串简支梁的弯距要大。
()原因:7.荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
()原因:8.图示为一杆段的M、Q 图,若Q 图是正确的,则M 图一定是错误的。
()M图Q图题8 图题9 图9.图示结构的支座反力是正确的。
()10.在无剪力直杆中,各截面弯矩不一定相等。
()原因:11.图示梁的弯矩分布图是正确的。
()q题10 图题11 图12.图示刚架的弯矩分布图是正确的。
()Al l13.图示结构B 支座反力等于P/2 (↑)。
()题12 图题13 图14.图示梁的弯矩分布图是正确的。
()15.只要已知静定刚架杆件两端弯矩和所受外力,则该杆内力就可完全确定。
()原因:16.图示桁架有9 根零杆。
()17.图示对称桁架中杆1 至8 的轴力等于零。
()d题16 图题17 图题18 图18.图示桁架中,上弦杆的轴力为N = -P 。
()19.三铰拱的弯矩小于相应简支梁的弯矩是因为存在水平支座反力。
()原因:20.在相同跨度及竖向荷载下,拱脚等高的三铰拱,其水平推力随矢高减小而减小。
()原因:21.简支支承的三角形静定桁架,靠近支座处的弦杆的内力最小。
()原因:22.组合结构中,链杆的内力是轴力,梁式杆的内力只有弯矩和剪力。
()原因:23.图示结构中,支座反力为已知值,则由结点D 的平衡条件即可求得N CD 。
()ED aDB C 4 a题23 图题24 图24.图示结构中,CD 杆的内力N1 = -P 。
结构力学静定多跨梁例题
摘要:
一、结构力学与静定多跨梁的基本概念
二、静定多跨梁的受力分析
三、静定多跨梁的弯矩图绘制
四、静定多跨梁的计算方法与步骤
五、结论与思考
正文:
结构力学是力学的一个重要分支,主要研究土木建筑、机械工程等领域中的结构受力、变形、稳定等问题。
在结构力学中,静定多跨梁是一个基本的构件,其受力分析是学习结构力学的重要内容。
静定多跨梁是指在两端固定、中间支撑的情况下,梁的支座反力和梁的弯矩可以通过静力平衡方程求解的多跨梁。
在受力分析时,需要考虑梁所受的外力、内力和温度变化等因素。
绘制静定多跨梁的弯矩图是结构力学中的一个重要任务。
弯矩图反映了梁在受力过程中各点的弯矩变化情况,通过弯矩图可以了解梁的受力状态,为结构设计和分析提供依据。
在计算静定多跨梁时,通常采用力法、位移法等方法。
其中,力法是通过列力平衡方程求解梁的支座反力和弯矩;位移法是通过列位移平衡方程求解梁的支座反力和弯矩。
在实际计算中,还可以采用矩阵法、图形法等方法,以简化计算过程。
总之,结构力学静定多跨梁是结构力学中的一个基本问题,其受力分析、弯矩图绘制和计算方法是学习结构力学必须掌握的内容。
1、杆系结构中梁、刚架、桁架及拱的分类,是根据结构计算简图来划分的。
(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。
(错误)3静力和动力荷载的区别,主要是取决于它随时间变化规律、加载速度的快慢。
其定性指标由结构的自振周期来确定。
(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动,(正确)又不能相对转动。
(错误)5、线弹性结构是指其平衡方程是线性的,(正确)变形微小,(正确)且应力与应变之间服从虎克定律。
(正确)1、学习本课程的主要任务是:研究结构在各种外因作用下结构内力与()计算,荷载作用下的结构反应;研究结构的()规则和()形式等问题。
正确答案:位移,动,组成,合理2、支座计算简图可分为刚性支座与弹性支座,其中刚性支座又可分为()、()、()和()。
正确答案:链杆,固定铰支座,固定支座,滑动支座3、永远作用在结构上的荷载称为固定荷载,暂时作用在结构上的荷载称为()它包括()、()、()、()和()等正确答案:活载,风,雪,人群,车辆,吊车4、刚节点的特性是被连接的杆件载连接处既无()又不能相对();既可传递(),也可传递()正确答案:移动,转动,力,力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。
()O正确答案:正确2、两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必须满足的条件。
()正确答案:正确3、在图示体系中,去掉1-5,3-5,4-5,2-5,四根链杆后,的简支梁12,故该体系具有四个多余约束的几何不变体系。
()12345正确答案:错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
()正确答案:错误5、图示体系是几何不变体系。
()正确答案:错误2-2几何组成分析1.正确答案:几何不变,且无多余联系。
2.(图中未编号的点为交叉点。
)A B CDEF正确答案:铰接三角形BCD视为刚片I,AE视为刚片II,基础视为刚片III;I、II间用链杆AB、EC构成的虚铰(在C点)相连,I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联,II、III 间由链杆AF和E处支杆构成的虚铰相联3.(图中未画圈的点为交叉点。