结构力学 第三章 作业参考答案
- 格式:pdf
- 大小:335.32 KB
- 文档页数:18
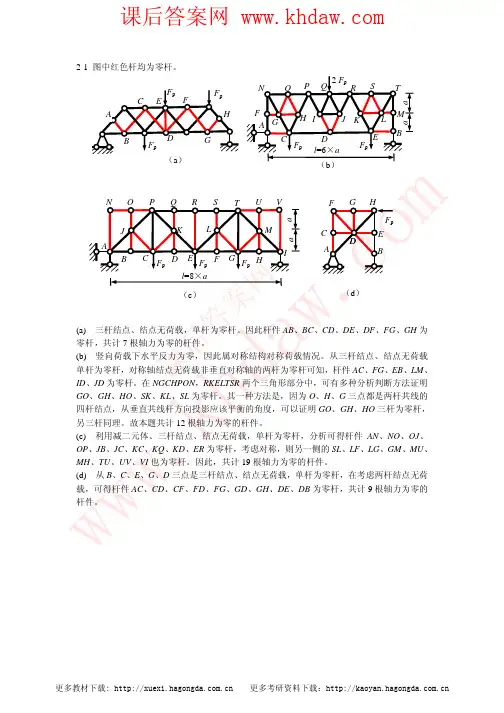
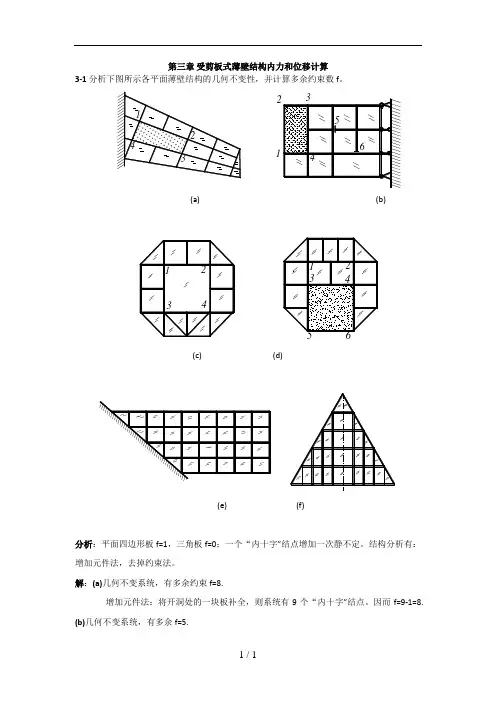
第三章 受剪板式薄壁结构内力和位移计算3-1分析下图所示各平面薄壁结构的几何不变性,并计算多余约束数f 。
1(a)(b)(c) (d)(e) (f)分析:平面四边形板f=1,三角板f=0;一个“内十字”结点增加一次静不定。
结构分析有:增加元件法,去掉约束法。
解:(a)几何不变系统,有多余约束f=8.增加元件法:将开洞处的一块板补全,则系统有9个“内十字”结点。
因而f=9-1=8.(b)几何不变系统,有多余f=5.增加元件法:将开洞处的一块板补全,切开端口杆的杆端处连上,则系统有4个“内十字”结点,外部多余约束数为3,对于端口切开的杆:丁字节点6处为零力杆端切开与否对静不定次数无影响,而处于“内十字”结点处的5处,则解除一次静不定。
因而f=4+3-1-1=5.(c)几何不变系统,有多余约束f=4.有4个“内十字”结点。
因而f=4.(d)几何不变系统,有多余约束f=3.增加元件法:将开洞处的一块板补全,则系统有4个“内十字”结点。
因而f=4-1=3.(e)几何不变系统,有多余约束f=21.有21个“内十字”结点。
因而f=21.(f)几何不变系统,有多余约束f=12.有12个“内十字”结点。
因而f=12.3-2分析下图所示空间薄壁结构的几何不变性,并计算多余约束数f。
(a)(b)(c) (d)(e)(f)(g) (h)6(i)(j)67(k)(l)78(m) (n)(o)分析:三缘条盒段若以四边形面与基础连接则有1次静不定(进行结构分析:视结点为自由体有3个自由度,板和杆各自起一个约束作用),若以三边与基础相连则为无多余约束的静定结构;对于一端固定的一段空心薄壁结构,端框有n个结点,其静不定次数为(n-3),故单边连接的四缘条盒段有1次静不定;对于四缘条盒段若以相邻两面和基础相连则由结构分析可知有3次静不定;对于三缘条盒段若以一边为三角形另一边为四边形和基础相连则由结构分析可知有2次静不定,若以双边四边形形式连接三缘条盒段则静不定次数为3。



第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
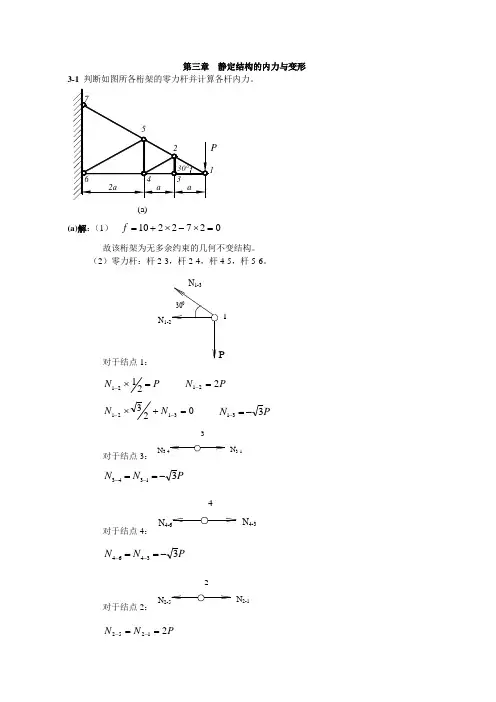
第三章 静定结构的内力与变形3-1 判断如图所各桁架的零力杆并计算各杆内力。
1P(a) (a)解:(1)0272210=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆2-3,杆2-4,杆4-5,杆5-6。
对于结点1:N 1-2PN 1-33001P N =⨯-2121 P N 221=-0233121=+⨯--N N P N 331-=-对于结点3:N 3-43N 3-1P N N 31343-==--对于结点4:N 4-64N 4-3P N N 33464-==--对于结点2:N 2-52N 2-1PN N 21252==--对于结点5:N 5-75N 5-2P N N 22575==--(b)(b)解:(1)082313=⨯-+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆5-4,杆6-4,杆6-7,杆6-8,杆1-5。
对于结点5:P5N 5-8P N -=-85对于结点8:N 7-88N 5-8Fθ05528785=+⨯--N N P N 55287=-对于结点7:N 7-47N 7-8P N 55247=-对于结点4:N 3-44N 7-4P N N 5524743==--对于结点3:N 1-33N 3-4P N N 5524331==--2(c)(c)解:(1)026228=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆4-3,杆4-6。
对于结点1:N 1-61N 1-3Pθ05561=+⨯-P N P N 561-=-05526131=⨯+--N N P N 231=-对于结点3:3N 3-1N 3-5P N N 21353==--(e)(d)解:(1)02112316=⨯-⨯+=f故该结构为无多余约束的几何不变结构。
(2)零力杆:杆4-5,杆5-6,杆4-6,杆7-6,杆2-3,杆2-8,杆2-9,杆1-2,杆9-11,杆8-9,杆9-11.对于结点4:4N 4-7N 3-4450PP N 2243=- P N 2274=-对于结点7:7N 4-7N 3-7N 8-7P N N 22227374=⨯-=-- P N -=-73P N 2278=-对于结点3:3N 3-4N 3-7N 8-7022734332=⨯+=---N N N P N 2283=-对于结点8:022228982=⨯⎪⎭⎫ ⎝⎛+=--N P N运用截面法:N 1-2N 9-10N 9-11PP23456789由对9点的力矩平衡:0222221=⨯⨯-⨯+⨯-P a P a a N 021=-N对于结点9:9N 2-9N 9-11N 9-10N 9-88911910922---=⨯+N N N P N 22109-=-8N 3-8(e)(e)解:(1)024125=⨯-++=f故该结构为无多余约束的几何不变结构。
第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
( )(a)(b)(c)习题 2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题 2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题 2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题 2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。


第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p7、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移∆DV 。
EI = 常数,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数。
l l l /3/3q13、图示结构,EI=常数,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数。
16、求图示刚架中D点的竖向位移。
EI=常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI =常数。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l/219、求图示结构A、B两截面的相对转角,EI =常数。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
l l21、求图示结构B 点的竖向位移,EI =常数。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
第三章静定结构的内力与变形3-1判断如图所各桁架的零力杆并计算各杆内力。
P(a)(a)解:(1)272210=×−×+=f 故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆2-3,杆2-4,杆4-5,杆5-6。
对于结点1:N 1-2PN 1-33001P N =×−2121PN 221=−0233121=+×−−N N PN 331−=−对于结点3:N 3-43N 3-1PN N 31343−==−−对于结点4:N 4-64N 4-3PN N 33464−==−−对于结点2:N 2-52N 2-1PN N 21252==−−对于结点5:N 5-75N 5-2PN N 22575==−−杆件1-21-32-32-42-53-45-45-65-74-6内力P2P3−0P2P3−0P2P3−(b)(b)解:(1)082313=×−+=f 故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆5-4,杆6-4,杆6-7,杆6-8,杆1-5。
对于结点5:P5N 5-8PN −=−85对于结点8:N 7-88N 5-8Fθ5528785=+×−−N N PN 55287=−对于结点7:N 7-47N 7-8PN 55247=−对于结点4:N 3-44N 7-4PN N 5524743==−−对于结点3:N 1-33N 3-4PN N 5524331==−−杆件1-31-21-52-32-43-44-54-65-86-76-87-84-7内力P5520P5520P −0P 552P552(c)(c)解:(1)026228=×−×+=f 故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆4-3,杆4-6。
对于结点1:N 1-61N 1-3Pθ5561=+×−P N PN 561−=−05526131=×+−−N N PN 231=−对于结点3:3N 3-1N 3-5PN N 21353==−−杆件1-21-31-62-32-43-43-54-6内力P2P 5−0P20(e)(d )解:(1)02112316=×−×+=f 故该结构为无多余约束的几何不变结构。
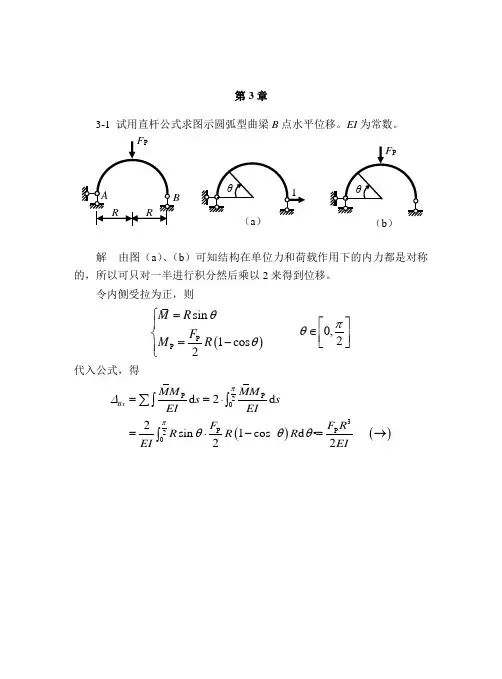
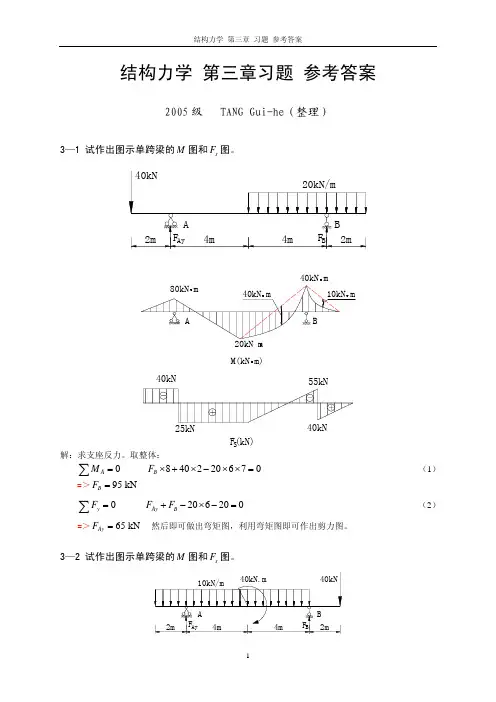
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答:由图(a)、(b)可知结构对称(水平反力为零)荷载对称,因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R(1−cos θ)M P = θ∈[0,π/2];M=R sin θθ∈[0,π/2]2 代入位移计算公式可得M P M 1 π2 M P M 2 π2 F P R(1−cos θ)∆Bx = ∑∫ EI d s = 2⋅EI ∫0 EI R dθ= EI ∫0 2 R sin θR dθ=F P R3 =(→)2EI3-1 (b) 答:如图(a)、(b)可建立如下荷载及单位弯矩方程pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R dθ= qEI 4 ∫0π2 (1−2cosθ+cos 2 θ)R dθqR 4 ⎡ θ 1 ⎡3π ⎡ qR 4= EI ×⎡θ−2sinθ+ 2 + 4sin2θ⎡⎡0 =⎡⎡ 4 − 2⎡⎡ 2EI (→)2 ⎡3-2 答:作M P 图和单位力弯矩图如下图: 由此可得内力方程代入位移公式积分可得2 2 P 0s i n ( ) d (c o s ) (c o s )q M R q R M R θθ α α θ θ − == − = − ∫AqRBα θ( a θ( b )根据题意 EI (x ) = EI (l + x )2l 代入位移公式并积分(查积分表)可得M P M l2 q 0x 4∆Bx =∑∫ EI d x =∫0 6EI (l + x ) d x7 q 0l 4 ql 4= (ln 2− )× =(→)12 3EI EI3-3 答:分别作出荷载引起的轴力和单位力引起的轴力如下图所示:由此可得 C 点的竖向为移为:1 lM 图 x3 0 p x q M M xl= = xP M 图2 0 6q lABl q 05 83 8F NP F N1 F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =6 5kN× ×6 m+2× kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 8 8EA=×10−4 m当求CD 和CE 杆之间的夹角改变使:施加如图所示单位广义力并求作出F N2 图,则F∆=∑∫ F NP EA F N2 ds=∑ NP EA F N2 l2× kN×(−×5 m+(− kN)××6 m =EA=−×10−4 rad ( 夹角减小)3-4 (a)答:先作出M p和M 如右图所示。