量子力学教程-周世勋-第六章散射
- 格式:pdf
- 大小:313.56 KB
- 文档页数:21

量子力学讲义周世勋高等教育出版社目 录第一章 量子理论基础 (1)1.1引言 (1)1.2 普朗克假设 (1)1.3 光电效应与光子 (5)1.4 玻尔理论 (7)1.5 波粒二象性 (9)第二章 波函数和薛定谔方程 (12)2.1 波函数的统计解释与态叠加原量 (12)2.2 狄拉克(Dirae)函数和平面波的归一化 (14)2.3 薛定谔方程 (19)2.4 粒子流密度和粒子数守恒定律 (21)2.5 波函数的标准条件 (22)2.6 定态问题 (24)2.7 求解散定态薛定谔方程的分离变量法 (25)2.8 本征方程 (31)2.9 一维对称方势附 (34)2.10 势垒贯穿 (40)2.11 一维谐振子 (43)2.12 转道角动量符 (47)2.13 类氢离子 (52)2.14 球谐原子 (57)第三章 算符和力学的量算符 (64)3.1 算符概述 (64)3.2 算符的对易关系 (66)3.3 线性厄密算符和力学量算符 (69)3.4 两个力学量同时有确定值的条件和测不准关系 (75)3.5 力学量平均值随时间的变化和守恒定律 (79)第四章 表象理论 (84)4.1 态的表象变换和态的矩阵表示 (84)4.2 算符的表象变换和算符的矩阵表示 (86)4.3 希耳伯特(Hilbert)空间与狄拉克符号 (90)4.4 量子力学公式的矩阵表示 (95)4.5 幺正变换 (97)4.6 薛定谔表象和海森伯表象 (101)4.7 线性谐振子与占有数表象 (105)第五章 近似方法 (111)5.1 非简并定态微扰论 (111)5.2 简并能级的定态微扰论 (117)5.3 氢原子的一级斯塔克(Stark)效应 (119)5.4 变分法 (124)5.5 求氦原子基态能量的变分近似法 (126)5.6 含时微扰论 (129)5.7 跃迁几率的计算 (134)5.8 原子对光的吸收与发射 (143)5.9 选择定则 (148)第六章 散射 (153)6.1 两体碰撞和散射截面 (153)6.2 有心力场中的弹性散射(分波法) (156)6.3 球方势阱和球方势垒对粒子的散射 (161)6.4 平面波玻恩(Born)近似 (165)6.5 质心坐标系与实验室坐标系 (171)第七章 自旋与角动量 (174)7.1 电子的自旋 (174)7.2 角动量 (175)7.3 自旋算符 (179)7.4 自旋为12的粒子的波函数 (182)7.5 带电粒子在电磁场中的运动 (184)7.6 两个角动量的相加 (190)7.7 原子光谱的精细结构 (195)第八章 全同粒子 (200)8.1 全同粒子的特性 (200)8.2 全同粒子的波函数和泡利不相容原理 (202)8.3 两个电子的自旋波函数 (206)8.4 两个全同粒子的弹性弹射 (210)8.5 氦原子 (214)8.6 氢分子 (219)第九章 量子力学回顾与展望 (225)。

1量子力学课后习题详解第一章量子理论基础1.1由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λT=b (常量);并近似计算b 的数值,准确到二位有效数字。
解根据普朗克的黑体辐射公式dv ec hvd kThv vv 11833−⋅=πρ,(1)以及c v =λ,(2)λρρd dv v v −=,(3)有,118)()(5−⋅=⋅=⎟⎠⎞⎜⎝⎛−=−=kT hcv v e hc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:201151186'=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−⋅+−−⋅=−kThc kThce kT hc ehc λλλλλπρ⇒115=−⋅+−−kThc ekThc λλ⇒kThc ekThc λλ=−−)1(5如果令x=kThcλ,则上述方程为xe x =−−)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知Km T m ⋅×=−3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e µ<<动),那么ep E µ22=如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0×,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λ3nmm mE c hc E h e e 71.01071.031051.021024.1229662=×=××××===−−µµ在这里,利用了meV hc ⋅×=−61024.1以及eVc e 621051.0×=µ最后,对Ec hc e 22µλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。


1量子力学课后习题详解第一章量子理论基础1.1由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λT=b (常量);并近似计算b 的数值,准确到二位有效数字。
解根据普朗克的黑体辐射公式dv ec hvd kThv vv 11833−⋅=πρ,(1)以及c v =λ,(2)λρρd dv v v −=,(3)有,118)()(5−⋅=⋅=⎟⎠⎞⎜⎝⎛−=−=kT hcv v e hc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:201151186'=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−⋅+−−⋅=−kThc kThce kT hc ehc λλλλλπρ⇒115=−⋅+−−kThc ekThc λλ⇒kThc ekThc λλ=−−)1(5如果令x=kThcλ,则上述方程为xe x =−−)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知Km T m ⋅×=−3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e µ<<动),那么ep E µ22=如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0×,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λ3nmm mE c hc E h e e 71.01071.031051.021024.1229662=×=××××===−−µµ在这里,利用了meV hc ⋅×=−61024.1以及eVc e 621051.0×=µ最后,对Ec hc e 22µλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。

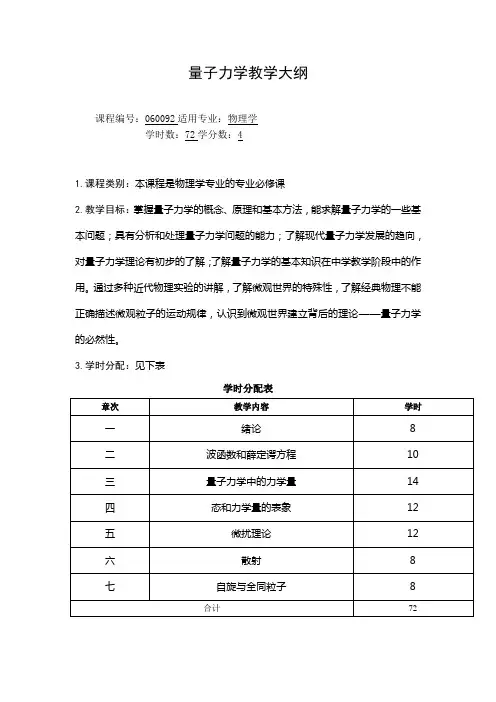
量子力学教学大纲课程编号:060092适用专业:物理学学时数:72学分数:41.课程类别:本课程是物理学专业的专业必修课2.教学目标:掌握量子力学的概念、原理和基本方法,能求解量子力学的一些基本问题;具有分析和处理量子力学问题的能力;了解现代量子力学发展的趋向,对量子力学理论有初步的了解;了解量子力学的基本知识在中学教学阶段中的作用。
通过多种近代物理实验的讲解,了解微观世界的特殊性,了解经典物理不能正确描述微观粒子的运动规律,认识到微观世界建立背后的理论——量子力学的必然性。
3.学时分配:见下表学时分配表第一章绪论教学时数:8学时重点难点:重点:了解经典物理遇到的困难,量子力学的建立过程。
微光粒子的波粒二象性。
难点:波粒二象性矛盾性的解释。
教学要求:了解:经典物理学的困难。
理解:波粒二象性矛盾性的辩证统一解释。
掌握:波粒二象性模型:λhP =的物理意义与它所包括的科学价值。
光的波粒二象性。
原子结构的波尔理论。
微光粒子的波粒二象性。
教学内容:(1)经典物理学的困难(2)光的波粒二象性(3)原子结构的波尔理论(4)微光粒子的波粒二象性第二章波函数和薛定谔方程教学时数:10学时重点难点:重点:波函数的统计解释,薛定谔方程的建立过程,用定态薛定谔方程处理势阱问题和线性谐振子问题。
难点:线性谐振子求解问题。
势垒贯穿。
教学要求:了解:量子力学理论的数学表示方式:薛定谔波动方程;波函数的统计解释。
理解:波粒二象性矛盾性的辩证统一解释——波函数的统计解释。
掌握:波函数的统计解释;定态薛定谔方程;一维无限深势阱的求解问题;定态薛定谔方程处理势阱问题和线性谐振子问题。
教学内容:(1)波函数的统计解释(2)态叠加原理(3)薛定谔方程(4)粒子流密度和粒子数守恒定律(5)定态薛定谔方程(6)一维无限深势阱(7)线性谐振子(8)*势垒贯穿第三章量子力学中的力学量教学时数:14学时重点难点:重点:表示力学量的算符;厄密算符本征函数的正交性;算符与力学量的关系。

量子力学课后习题详解第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。


量子力学教程周世勋_课后答案(共88页)-本页仅作为预览文档封面,使用时请删除本页-量子力学课后习题详解 第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc e kThcλλ⇒ kThcekThcλλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。


量子力学课后习题详解第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。