当前位置：文档之家 › 第六章散射理论

第六章散射理论

  • 格式：ppt
  • 大小：19.95 MB
  • 文档页数：58

下载文档原格式

  / 58

合集下载

第六章_光的吸收、散射与色散

第六章_光的吸收、散射与色散
I I0 (1 cos2 )
是散射光方向与入射光方向之间的夹角。
可见，散射光 强的分布是对 于光的传播方 向及垂直于光 的传播方向是 对称的。
散射光方向
入射光方向
虽然从光源发出的光是自然光，但从正侧方用检偏器检 查发现，散射光是线偏振的，沿着斜侧面观察发现是部 分偏振光，只有正对着入射方向观察时，透射光才是自 然光。
数，其数值由实验数据来确定，当波长变化范围不大
时，科希公式可只取前两项，即
n
A
B
2
则介质的色散率为：
dn
d
2B
3
A、B均为正值，上式表明，折射率和色散率的数值 都随波长的增加而减小，当发生正常色散时，介质的 色散率小于零。
二. 反常色散
对介质有强烈吸收的波段称为吸收带。实验表明，在强 烈吸收的波段，色散曲线的形状与正常色散曲线大不相 同。
当光通过介质时，不仅介质的吸收使透射光强减弱，由于 光的散射也使使射入介质的光强按指数形式衰减，因此， 穿过厚度为l 的介质透射光强为：
I I0e( )
为吸收系数，为散射系数，+就称为衰减系数。在 很多情况下，和中一个往往比另一个小很多，因而可 以忽略。
三. 散射光强的角分布和偏振态
实验表明，散射光的强度随光的方向而变化，自然 光入射时，散射光强满足下式：
假设入射光是线偏振的，传播方向沿着Z轴，如图。设
在各向同性的介质中有一粒子P。
当光与粒子相遇时，使P作
x
受迫振动，所形成的电矢量
也平行于X轴。由此产生的
次波为球面波。光波又是横
波，振动方向与传播方向垂
直。在各个方向的振幅应等 y
于最大振幅在相应方向的投
影。

第六章光的色散吸收散射瑞利散射米氏散射光偏振性

第六章光的色散吸收散射瑞利散射米氏散射光偏振性

米氏散射和瑞利散射的规律不同，它产生的散射与波长的 关系不大，几乎所有波长的光都含有，所以看起来是白色光。 也是是否看到蓝天白云的根本原因。也是人工降雨的理论基础。
8
黄山风景山中的雾气实际上是悬浮在空气中的小液滴，是 一种很理想的散射源。由于液滴的尺寸比光波波长大得多，主 要是米氏散射，散射光呈白色。
10
一幢大楼晚上楼顶上的几束强光刺破夜空，能看到这几 道光束，就是散射的作用。如果城市上空的空气不干净，悬 浮尘埃越多，散射就越强，光束就会显得很亮。反之，光束 就会显得很淡。如果晚上基本上看不到这几道光束了，也许 白天城市就会有蓝色的天空了。 思考：如果没有空气，天空又会是什么样的呢？
11
4 散射光的偏振性
4
3 瑞利散射
把线度小于光的波长的微粒对入射光的散射， 称为瑞利散射（Rayleigh scattering）。 瑞利散射不改变原入射光的频率。 1 I散 4
瑞利散射时，由于蓝光波长较短，其散射强度就比波长 较长的红光强，因此散射光中蓝光的成份较多。
5
注意画面上的香火形成的烟雾呈现出一种浅蓝色这是由于 组成烟雾的碳粒子线度非常小，由这些烟雾产生的散射光符合 瑞利散射的条件，因此散射光中的蓝光成份比红光成份强得多。 我们平时所说的“袅袅青烟。”说是就是这种瑞利散射所产生 的现象。
§6.3 光的散射 问：天空为什么是蓝的？旭日和夕阳为什么是红 的，而中午的太阳看起来又是白的？云为什么是 白的？如果没有空气，天空又会是什么样的呢？
1 光的散射现象
当光束通过均匀的透明介质时，从侧面是难以看到光 的。但当光束通过不均匀的透明介质时，则从各个方向都 可以看到光，这是介质中的不均匀性使光线朝四面八方散 射的结果，这种现象称为光的散射。 例如，当一束太阳光从窗外射进室内时，我们从侧面 可以看到光线的径迹，就是因为太阳光被空气中的灰尘散 射的缘故。

光的吸收、色散和散射

光的吸收、色散和散射
※ 组成物质的原子或分子内的带电粒子（电子或离子）被准弹性力保 持在它的平衡位置并且有一定的固有振动频率
※ 在入射光作用下，原子或分子发生极化，并以入射光频率作受迫振 动，形成振动的电偶极子，从而发出次波
※ 在均匀介质中，这些次波叠加的结果使光只在折射方向继续传播下 去，而在其它方向上次波的干涉而相互抵消，没有出现光
或 dn
d
（6-21） （6-22）
一、正常色散 折射率随波长增加而减小的色散 ---正常色散
正常色散可以用科希（Canchy）公式来描写
n
A
B
2
C
4
（6-23）
通过三个波长实验测量3个n ---即可得A，B，C三个常数
对于波长间隔不太大时，可只取前两项：
n
A
B
2
（6-24）
dn
d
2B
3
（6-8） （6-9）
折射率 n 为复折射率
n2
r
1
1
Ne2
0m
1
02 2
i
同理 n 可写为
n n i
n2 n2 2 i2n
将（6-11）与（6-10）相对照，可得
n2 2 1 Ne2
0m
02 2 02 2 2 22
2n Ne2
0m
02 2 2 22
光束通过不均匀介质所产生的偏离原来传播方向而向四周散射的现象
散射分类： 1、k变化，波长不变
廷德尔散射 分子散射
瑞利散射，米氏散射
2、 k变化，波长也变化
Raman散射 Brillouin散射
廷德尔散射：液体、气体中悬浮粒子（包括尘埃）、大气中气溶胶、 烟雾等产生的散射
瑞利散射：颗粒大小< 1

量子力学-第六章散射(碰撞)

量子力学-第六章散射(碰撞)
r
8
单位时间内穿过半径为R球面上dS的粒子数
其中
dn
jrdS v
f
( , )
2
dS r2
v
f (,) 2 d
jr
i 2m
( 2
r
2
2
r
2
)
v r2
f ( ,) 2 v
k m
由定义式： dn q(,) jd
因为
j
i 2m
(
1
1
z
1
1 )
z
k m
v
所以 dn q(,)vd
故有 q( ,) f ( ,) 2
2
Q 0 0 q( ,)d
粒子被散射到空间各方向上的几率和。 7
2.微分散射截面与散射振幅的关系
设入射粒子： 质量m， 动量 k 波函数 1 eikz
出射粒子：质量m ， 动量 k
波函数
2
fห้องสมุดไป่ตู้
( ,) eikr r
其中f(,)为散射振幅. r→处的波函数：
reikz f ( ,) eikr
l
)
Al
sin(kr l 2
kr
π
l )
12
r
l 0
Al kr
sin(kr
1 2
lπ
l
)Pl
(cos
)
另一方面
eikz eikrcos (2l 1)il jl (kr)Pl (cos ) l0
根据球贝塞耳函数在无穷远处的渐进行为
r
l0
(2l
1)il
1 kr
sin(kr
1 2
lπ)
S
d
6

第六章 散射

第六章 散射

(r , , ) Rl (r )Ylm ( , )
l ,m
若选取粒子入射方向并通过散射中心的轴线为极轴，则 中心力场的散射问题具有轴对称性，波函数及散射振幅都与 无关，即 m 0 ，所以有
(r , , ) Rl (r )Pl (cos )
l
（11）
u l (r ) Rl (r ) r
（13）
d 2 u l (r ) 2 l (l 1) （14） k V ( r ) 2 2 u l ( r ) 0 dr r u 这里， l (r ) 的函数形式尚依赖于U (r ) 的具体形式，考查 r
处的渐进形式，则上式简化为
能只与 r 大小有关，所以
2 [k 2 V (r )] 0
（9）
如前所述，实验上观测散射粒子都是在远离散射中心的地方
进行，所以我们总是关注波函数在 r 时的渐进行为。 • 而在无穷远处，不但有平面波存在，而且有散射波存在， 所以满足（9）式的波函数应具有如下的渐进行为（边界条 件）
•
散射过程实际上是由于空间小区域中的相互作用导 致的粒子从一个自由态到另一自由态的跃迁。但是，这种 跃迁的初末态能量是相同的，并且组成连续谱。本讲主要 讨论的仍属于跃迁概率问题，而中心问题是散射截面。散 射截面的计算，主要通过两种近似方法：分波法和玻恩近 似法。 • 1 散射截面 • 1、1 入射 设自由粒子流沿着 轴向散射中心入射。首先，我 们定义：单位时间内穿过垂直于入射方向的单位面积的入 射粒子数为入射粒子流强度，记为 N 。从波动理论出发， 入射波取为 （1） 1 e ikz
2.分波法 • 2.1薛定谔方程及其边界条件 若入射粒子与散射中心之间的相互作用势能用中心力 场 U (r )表示，并假定 lim U (r ) 0 ，则体系的薛定谔方程写 r 为

第六章 散射和吸收

第六章 散射和吸收

第六章散射和吸收（Scatter and Absorption）§6.1描述衰减的术语（Terms Describing Attenuation）§6.2辐射传输方程Ⅰ（Radiative Transfer EquationⅠ）§6.3大气层和大气窗（Aerosphere & AtmosphericWindows）§6.4辐射传输方程Ⅱ（Radiative Transfer EquationⅡ）§6.1.1复折射率和穿透深度（Complex Index ofRefraction & transmittance depth ）复折射率（complex index of refraction ）的表达式如下它的实部n ′是折射率（refraction index ），它表明电磁波在两介质的界面处传播速度和方向的变化。

n n ′′−′=i n图6-1：折射和反射如图图6-1所示，在海-气界面，反映这种变化的是斯奈尔折射定律（Snell’s Refraction Law ）（6-2）式中n ′是电磁波从空气向海水传播时在海水的折射率，θ1是入射角，θ2是折射角，c 和v 分别是电磁波在空气和海水中传播的相速度（phase speed ），这里v 指复相速度的实部。

斯奈尔折射定律（Snell’s Refraction Law ）•使用测量折射的仪器可测得在可见光范围介质的折射率n ′。

如果已知海水的相对电容率εεr ，则可使用（6-3）来计算复折射率n = n ′−i n 〞•在微波波段里，相对电容率εεr 可从德拜方程获得。

复折射率的虚部表示电磁波在介质中传播的衰减程度。

把（,6-1）和（6-2）代入麦克斯韦方程组的解，可得到（6-4）式中E x （ω, z ）代表电场强度（electric field intensity ），ω= 2πf 代表电磁波的角频率（angular frequency ），z 是沿电磁波传播方向的坐标，E x0是电场强度（electric field intensity ）在传播过程开始点（z = 0）的振幅，脚标x 代表电场强度沿x 轴方向振动，它与电磁波的传播方向z垂直。

第六章 散射

第六章 散射

代入（ ），得径向方程 （3-2）代入（3-1），得径向方程
l (l + 1) 1 d 2 dRl 2 r dr + k − V (r) − r 2 Rl (r) = 0 2 r dr
（3-3）
16
三、分波法 (续2)
Chapter.6 .Scattering
4
一 散射截面 (续3)
Chapter.6 .Scattering
q(θ，ϕ)具有面积的量纲 q(θ
dn 2 [q] = =L NdΩ
为微分散射截面， q(θ 故称q(θ，ϕ)为微分散射截面，简称为截面 或角分布 如果在垂直于入射粒子流的入射方向取截 q(θ 面面积q(θ，ϕ)，则单位时间内通过此截面的 粒子数恰好散射到(θ，ϕ)方向的单位立体角 内。 dn q(θ , ϕ ) N = （2） ） dΩ
dn = q (θ , ϕ ) NdΩ
（ 1）
比例系数q(θ，ϕ)的性质： 比例系数q(θ q( 的性质：
性质， 它们之间的相互作用， 性质 ， 它们之间的相互作用 ， 以及入射粒子 的动能有关， 的动能有关，是θ，ϕ 的函数
q(θ，ϕ)与入射粒子和靶粒子（散射场）的 与入射粒子和靶粒子（散射场） q(θ
ikx
方程（ 方程（8）有两个特解
φ (r,θ ,ϕ ) = f (θ ,ϕ )e
ikr
−ikr
φ ′(r,θ ,ϕ ) = f (θ ,ϕ )e
10
二、散射振幅 (续4)
Chapter.6 .Scattering
r − ikr e ′ ψ 2 (r ,θ , ϕ ) = f (θ , ϕ ) r ψ 2 代表由散射中心向外传播的球面散射波， 代表由散射中心向外传播的球面散射波， ′ 代表向散射中心会聚的球面波， ψ 2 代表向散射中心会聚的球面波 ， 不是散射 应略去。 波，应略去。 在 r → ∞ 处 ， 散射粒子的波函数是入射平 ikz 之和。 面波 ψ 1 = e 和球面散射波 ψ 2 之和。即

量子课件9散射理论

量子课件9散射理论

无关，则：

0
Q
q， sindd
0
2
2
q sind
0
2
（4）
三、q， 的理论计算： （由薛定鄂方程出发）
表示入射粒 U r （在质心系中）取散射中心为坐标原点，用 子与散射中心之间的相互作用势，体系的波函数 满足薛定谔方
jr 2

2
2
r
* 2
f , 2 2 r 2 r r
2
k v 2 2 f , f , r2 r 2
它表示单位时间内穿过半径为r的球面上单位面积上的粒子数。
所以穿过球面上ds面的粒子数为：
将⒁式代入⑵式，并令⑵式与⑾式相等：
1 1 e ikr ( 2l 1)i sin( kr l ) Pl (cos ) f ( , ) kr 2 r l 0 A 1 l sin( kr l l ) Pl (cos ) (15) 2 l 0 kr
（r） r ,， R （ （， ） l r）Ylm
l ,m

因为ψ(r)与φ无关，所以m=0，则上式变为：
（r ） r , Rl ( r ) Pl ( cos )
l 0

( 3)
在这个展开式中，每一项称为一个分波， Rl (r ) Pl (cos ) 是第l个分波，每个分波都是方程⑴的解，通常称l=0,1,2,……的 分波分别是s,p,d,……分波，相应的散射称为s散射，p散射等。
为便于比较，需将平面波 e
ikz

按球面波展开
e
ikz
e
ikr cos
（ 2l 1 ）i l j（ （ l kr）P l cos）

第六章 散射和吸收

第六章 散射和吸收

第六章散射和吸收（Scatter and Absorption）§6.1描述衰减的术语（Terms Describing Attenuation）§6.2辐射传输方程Ⅰ（Radiative Transfer EquationⅠ）§6.3大气层和大气窗（Aerosphere & AtmosphericWindows）§6.4辐射传输方程Ⅱ（Radiative Transfer EquationⅡ）§6.1.1复折射率和穿透深度（Complex Index ofRefraction & transmittance depth ）复折射率（complex index of refraction ）的表达式如下它的实部n ′是折射率（refraction index ），它表明电磁波在两介质的界面处传播速度和方向的变化。

n n ′′−′=i n图6-1：折射和反射如图图6-1所示，在海-气界面，反映这种变化的是斯奈尔折射定律（Snell’s Refraction Law ）（6-2）式中n ′是电磁波从空气向海水传播时在海水的折射率，θ1是入射角，θ2是折射角，c 和v 分别是电磁波在空气和海水中传播的相速度（phase speed ），这里v 指复相速度的实部。

斯奈尔折射定律（Snell’s Refraction Law ）•使用测量折射的仪器可测得在可见光范围介质的折射率n ′。

如果已知海水的相对电容率εεr ，则可使用（6-3）来计算复折射率n = n ′−i n 〞•在微波波段里，相对电容率εεr 可从德拜方程获得。

复折射率的虚部表示电磁波在介质中传播的衰减程度。

把（,6-1）和（6-2）代入麦克斯韦方程组的解，可得到（6-4）式中E x （ω, z ）代表电场强度（electric field intensity ），ω= 2πf 代表电磁波的角频率（angular frequency ），z 是沿电磁波传播方向的坐标，E x0是电场强度（electric field intensity ）在传播过程开始点（z = 0）的振幅，脚标x 代表电场强度沿x 轴方向振动，它与电磁波的传播方向z垂直。

第六章散射

第六章散射

⎧− 3V0 , r ≤ a V r =⎨ r>a ⎩ 0,
()
。
（1’）
解：自旋为 1 2 的二全同粒子体系的总波函数必须是交换反对称的， s 波（ l = 0 ）波函 数是两粒子空间坐标的对称函数，所以自旋波函数必须是反对称的，即为自旋单态，因 此，体系总自旋为 0 ，亦即，
σ 1 ⋅ σ 2 = −3 ，
f (θ ) = −
2u h2 K
2
∫
∞
0
r 'V ( r ' ) sin Kr ' dr ' ， K = 2k sin
4u 2 h4 K 2
θ
2
，
（1） （2）
q (θ ) = f (θ ) =
a
∫
∞
0
r 'V ( r ' ) sin Kr ' dr '
2
，
（a） ∫ r ' ( −V0 ) sin Kr ' dr ' = −
−
亦即：h2 " 来自 + V (r )u = 0 2u
，
（3）
u " + k 02 u = 0 , r ≤ a u" = 0 , r>a
(E → 0 )
，
（3’）
其中：
k 0 = 6uV0 h = 3mV0 h
，
（4）
m 为粒子质量， μ = m 2 为两粒子体系的约化质量。
方程（3’）满足边界条件 u (0 ) = 0 的解为：
r≤a ⎧ A sin k 0 r , ⎪ ⎛ r ⎞ u (r ) = ⎨ C⎜ 1− ⎟ ⎜ ⎟, r >a ⎪ ⎩ ⎝ a0 ⎠

第六章 散射

第六章 散射

第六章 散射§6.1碰撞过程，散射截面散射实验在近代物理学的发展中起了特别重要的作用。

特别是在认识原子、分子、核及粒子的结构性质方面，Rutherford 的粒子散射→原子的结构。

从此揭开了原子结构的新篇章，夫兰克赫兹实验证明了玻尔关于原子有定态的假设，原子很小，很难看到其微观结构，只能通过粒子与其作用，探测其性质，结构,就像用石头探水深，投石问路的方式探测其结构。

散射现象也称为碰撞现象通过散射表现出的宏观现象，研究靶的结构性质Δ散射态是一种非束体态，涉及到体系能谱的连续区部分，人们可以自由地控制入射粒子的能量。

Δ束体态理论主要在于求体系的分立能量本征值，和本征态以及在外界作用下量子态之间的跃迁规律。

Δ散射主要关心散射粒子的角分布及散射过程中粒子各种性质的变化。

Δ散射实验所观测到的都是离靶“很远”地方粒子的行为o r a 因此关心波函数在r →∞的渐近行为。

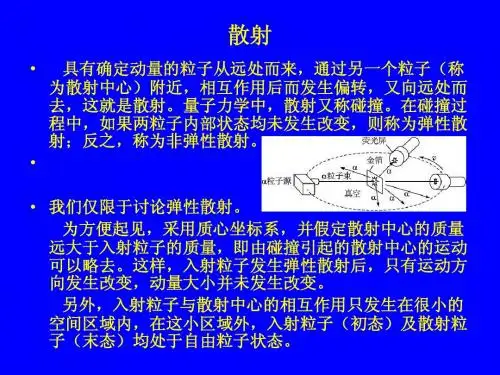
散射过程的一些基本概念①一粒子与另一粒子碰撞的过程中，只有动能变换，粒子内部状态无改变态，则称为弹性碰撞（散射）若碰撞中粒子内部状态有所改变，如原子被激发或电离，则为非弹性碰撞，注意和经典物理中物体碰撞的比较。

②粒子和另一粒子的散射实质是粒子与力场的作用，微观原子为靶时，实质是粒子与原子的作用，场电、电场、核力确定原子、粒子很小靶粒子称为散射中心，当靶A 的质量能入射粒子质量大得多时，可忽略靶的运动。

这样以来入射粒了受A 的作用偏离原来运动方向，发生散射于原来方向的夹解Q ，为散射角，如以极坐标描述，取入射粒子流方向为∂轴，则Q 用就为散射角。

研究dn单位时间内散射到面积元ds 上的粒子数dn ，当r 一定时，取求面上面积元ds 则，dn dx ∞当r 变化时2ds r ∞∴2ds dn d r∞=Ω即与ds 所张的立体角成正比，同时dn 与入射粒子流强度N 成正比N 定义，单位时间穿过单位横截面的粒子数 d n N d ∞Ω一般情下，不同方向(,)θϕ散射到的粒了数不同 (,)d N q N d θϕ=Ω(,)dn q Nd θϕ=Ω 当N 一定时，单位时间散射到(,)θϕ方向立体角ds 内的粒子数dn 由(,)q θϕ确定，(,)q θϕ与入射粒子，散射中心的性质等有关(,)q θϕ的量纲为2L面积 (,)dnq N d θϕ=Ω(,)q θϕ称为微分散射截面一个粒子(,)q d θϕΩ散到(,)θϕ方向d Ω立体内的几率 N 个粒子 (,)q Nd θϕΩ散到(,)θϕ方向d Ω立体内的个数 N 为单位时间入射粒子则(,)q Nd θϕΩ单位时 个数 将(,)q d θϕΩ对所有方向积分2(,)(,)sin ooQ q d q d dp ππθϕθϕθθ=Ω=⎰⎰⎰称为总截面量子力学如何处理散射？取散射中心为坐标原点，用()U r 表示入射粒子与散射中心之间的相互作用势能，则体系的薛方程为222U E ψψψμ-∇+=式中的μ为入射的质量，E 是它的能量为了方便，定交22222E p kμ==pkv μμ==22()()V r U r μ=hp k λ==2p k πλ==方程变为 22(())0k V r ψψ∇++=我们关心r →∞时ψ的行为，假设r →∞时()0U r →在粒子远离散射中心时，作用超于零，()U r 比1r 更快超于零，对电场不适用。

第六章 散射b

第六章 散射b

第六章 散射§6.1 学习指导实验上，人们从微观对象（如原子或原子核）中获取信息的主要渠道有两个：一是微观对象所发出的光或其他射线，二是该微观对象对入射光或其它粒子束的吸收和散射。

原子吸收或者发射光波的频率是离散的，谱线具有线状结构，说明原子具有能级，原子能级与其内部相互作用之间有密切的联系，这部分内容已经在前几章中作了介绍。

本章主要研究入射粒子束被一个作为靶粒子的微观对象所散射的问题，被散射后粒子的能量分布与出射角度分布反映了靶粒子的性质，通过对散射实验数据的分析可以了解靶粒子的内部结构与及其与散射粒子的相互作用。

散射可以分为弹性散射与非弹性散射，在弹性散射过程中入射粒子的能量保持不变，不涉及靶粒子内部状态的变化，相对比较单纯，是散射问题理论研究的基础。

非弹性散射过程可以按出射粒子的能量或者其他性质分为若干个反应道，对各个反应道的理论处理方法与弹性散射类似。

本章的重点是粒子束对中心势场的弹性散射，与粒子在中心势场的能级问题有密切的联系，在学习过程中与第三章相关内容进行比较，有助于我们对量子力学理论的全面理解。

必须注意：当靶粒子的质量为无穷大时，散射中心与靶粒子重合；当靶粒子质量有限时，散射中心为靶粒子和入射粒子的质心，入射粒子的质量应该修正为折合质量，所得到的散射截面也要作相应的变换。

本章的主要知识点有 1. 散射过程的描述 1）实验测量的描述以入射方向为极轴，散射中心为原点，入射粒子流在单位时间内散射到(,)θϕ方向立体角sin d d d θθϕΩ=内的粒子数为dn ，它与入射粒子流的强度N 和立体角的大小d Ω成正比，比例系数(,)/()q dn Nd θϕ=Ω (6-1)具有面积的量纲，称为微分散射截面。

微分散射截面等于单位强度的入射粒子流在单位时间内散射到(,)θϕ方向单位立体角内的粒子数，可以用实验直接测量。

微分散射截面对立体角进行积分后，得到总散射截面20(,)(,)sin Q q d d q d ππθϕϕθϕθθ=Ω=⎰⎰⎰⎰ (6-2)上式给出了散射粒子数与入射粒子数之比。

第六章光的散射

第六章光的散射

色散 Dispersion
同一物质中，光速 和波长 有关的现象叫色散。
dn 色散率D： D d
交叉棱镜装置 1672年 牛顿
n( )
倾斜光带的形状直观地反映了 两种材料色散性能的差异。
一. 正常色散和反常色散 在所取的频段中，若折射率 n 随波长 的增加 而单调下降，则称之为 正常色散。 无色透明材料 ( 例如玻璃 ) 在可见光范围是正常色散。 科希(Cauchy)公式 （1836年）：
三. 复数折射率
~ n 吸收可归并到一个 复折射率 中。在介质中沿z方向
~ E( z) A0 exp( iknz)
(2)
n c /
传播的的平面电磁波中电场强度可写作如下复数形式：
这里n是实数，k是光在真空中的波数, 电磁波不随距 离衰减。
若形式地将其看作复数，并记做
~ n n i
3. 用同种材料（即和R一定）制成的两块厚度不同的玻 璃片来做实验，用同样的入射光强I0，测定透射光强。设 厚度为l的玻璃片的透射光强为I2，厚度为l’的玻璃片的透 射光强为I’2 ，则
I2 2 l 1 R e I0
I 2 l ' 1 R e I0
' 2
二式相除，得
石英的色散曲线
反常色散总是与光的吸收有密切联系，一种物 质在某一波长区域内有反常色散时，则在该区 域内也有强烈的吸收。
固有频率0附近的折射率与吸收（经典电子理论）
M
N
在反常色散区ＭＮ内出现折射率随频率的增 大而减小的现象。
反常色散曲线
特点：折射率随波长的增大而增大，即色散率
dn 0 d
二. 一种物质的全部色散曲线 一般特征：一系列吸收带，两相邻吸收带之间，n 随 的增加而单调下降。每经过一个吸收带，n 显著 增大。曲线总趋势是随 增加而抬高。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

概率（粒子数）守恒（光学定理存在的依据 ）
（光的散射类似）
数学上，对入射粒子正前方向（ ），微分散射截面是有意义 的。但是由于正前方向，有入射与散射波的干涉，这样，就不能 区分究竟是散射粒子还是入射粒子。所以，在入射粒子正前方向 上，微分散射截面是一个没有直接观测意义的物理量。
事实上，在大多数情况下，在
如果总的哈密顿量旋转不变（例如有心力场）， （1）试讨论散射振幅 为什么不依赖于 （2）为什么这个讨论不能推广为 也不依赖于 （3）当入射波能量趋于0时 又如何？
注意：这里的 就是s波相移。因为当
时，函数 形式不变。
屏蔽因子
讨论：两体散射
方法：质心坐标系
理论工作者
附近，散射振幅是边续的，
所以，正前方向的散射振幅是一个完全确定的量。
正前方向的微分散射截面可以用外推法测量，即从 ，但在 附近（即非正前方向）测得微分散射截面，再用外推求出 方向的微分散射截面。
（理论上分波法是解决散射问题的普遍方法 ）
作业题 一个给定势对零自旋粒子的散射量子理论给出如下波函数的渐近 表达式
实验室坐标系 实验工作者
问题：在实验室坐标系
m1
v1
m2
静止

） 目的：找出实验室坐标系和质心坐标系描述两体散射的关系。
一、在静系中看：即实验室坐标系
s：散射角
二、在动系中看：即质心坐标系 质心系散射图
c为质心系散射角
在坐标系中
入射方向
(较好的选择!)
常系数
入射方向
必须有限
连续函数
显然，不同分波已经分离是独立的，各自满足相应的径向方程 。
为了与入射波的分波比较相位差。
各分波是独立地散射，没 有不同分波间的干涉。
入射波；
散射波；
相移 必与 有关。 散射势场的作用是改变第个 分波的径向波函数的渐近行为 即产生一个相移。
数以及在外界作用下的量子跃迁概率。
2、散射态 （Scattering state）： 在无穷远处波函数不为零的状态为散射态 。
（散射态边界条件 ）
散射态波函数不能归一化，能量可以连续取值，组成连续谱。 散射态问题中，势场和粒子的能量是已知的，求散射态的反射 系数、透射系数和相应的波函数以及角分布（散射截面）。
第六章散射理论
2020年4月19日星期日
1、束缚态（Bound state ）：
（束缚态边界条件
把在无限远处波函数为零的状态为束缚态。即粒）子被限制在一
个有限的范围内运动。
一般来说，束缚态体系的波函数可以归一化，能级是分立能级
组成分立谱。
能量量子化是束缚态粒子的共同特性，是微观世界的特有现象 。 束缚态问题中，势场是已知的，求束缚态的能级和相应的波函
注意：在量子力学中，入射粒子的概率流密度的意义是单位 时间内通过垂直入射方向单位面积的概率，它正是当单位时 间内只有一个粒子入射时的入射粒子流强度/密度。 的意义 就是单位时间内散射到 方向 立体角内的概率。
（短程势）
为什么研究散射问题时，通常只限于势场作用范围外的散射波 ？
（1）在势场范围内求出被散射粒子的状态是极其复杂的。而 在势场之外，由于可推知渐近解的形式，比较容易处理。这 样，不必求出势场范围内的解即可求出散射截面。
（2）我们观察散射现象，收集被散射的粒子，由于实验手段 是宏观的，一般必在距离散射中心从微观上是无穷远的地方 ，即在势场作用范围之外。因此计算势场范围以内的解也是 不必要的。散射截面正是势场作用范围外定义的。
散射态的边界条件（从物理上考虑得出
）
代表沿z轴方向入射的粒子。
代表离开散射中心向所有方向出射的粒子 。