图上距离与实际距离

六年级数学比例尺的知识点一、比例尺的定义。

1. 比例尺表示图上距离与实际距离的比。

例如，一幅地图的比例尺是1:10000，表示图上1厘米代表实际距离10000厘米（也就是100米）。

2. 比例尺的公式为：比例尺 = 图上距离:实际距离，也可以写成(图上距离)/(实际距离)。

二、比例尺的分类。

1. 数值比例尺。

- 数值比例尺是用数字的比例式或分数式表示比例尺的大小。

如1:500，(1)/(500)，这种比例尺的前项或分子通常为1。

- 数值比例尺的特点是直观地表示出图上距离和实际距离的倍数关系。

例如，比例尺1:500表示图上距离是实际距离的(1)/(500)，实际距离是图上距离的500倍。

2. 线段比例尺。

- 线段比例尺是在地图上画一条线段，并注明地图上1厘米所代表的实际距离。

例如，在一幅地图上有这样的线段比例尺：0 50 100 150千米，它表示图上1厘米代表实际距离50千米。

- 线段比例尺的优点是可以直接从图上量出距离，然后根据比例尺算出实际距离，比较直观。

三、比例尺的应用。

1. 根据比例尺和图上距离求实际距离。

- 已知比例尺和图上距离，根据实际距离 = 图上距离÷比例尺来计算。

例如，在比例尺为1:2000的地图上，量得学校到图书馆的图上距离是5厘米，那么实际距离 = 5÷(1)/(2000)=5×2000 = 10000厘米 = 100米。

2. 根据比例尺和实际距离求图上距离。

- 已知比例尺和实际距离，根据图上距离 = 实际距离×比例尺来计算。

例如，实际距离为300米，比例尺为1:10000，先将300米换算成30000厘米，图上距离 = 30000×(1)/(10000)= 3厘米。

3. 比例尺在图形放大与缩小中的应用。

- 在将图形按一定比例放大或缩小的时候，比例尺也起到重要作用。

例如，把一个三角形按2:1放大，就是把三角形的每条边都扩大到原来的2倍，这里的2:1就是放大的比例尺。

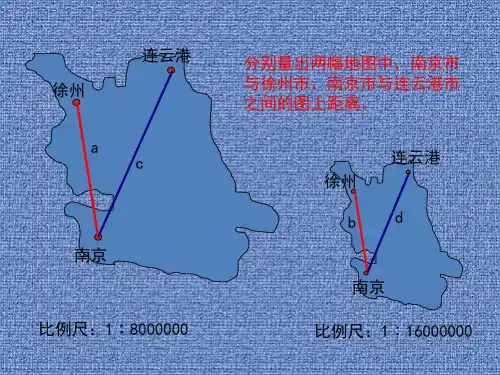
小升初专题比例尺1.比例尺的概念：一幅图的图上距离和实际距离的比，叫做这幅图的比例尺。

2.图上距离:实际距离 = 比例尺或＝比例尺实际距离图上距离 注意：（1）比例尺是一个比，他表示图上距离和实际距离的倍比关系，因此不能带有计量单位。

（计算时要先统一单位）（2）比例尺是图上距离比实际距离得到的最简整数比，可以写成带比号的形式，也可以写成分数形式。

（3）在大小相同的地图上，比例尺越大，反映的实际范围越小。

3.比例尺的分类数值比例尺： 1:100000000或1000000001 线段比例尺：线段比例尺可以改写成数值比例尺，比如：1cm:50km = 1cm:5000000cm = 1:50000004.缩小比例尺：在绘图时，根据需要把实际距离按一定的比例缩小，在纸上画出来。

为了计算方便，一般把缩小比例尺写成带比号的形式时，写成1:（ ），或者()1.放大比例尺：对于机器零件比较小，有时需要把实际距离扩大一定的倍数以后，再画在纸上，这样的比例尺就称为放大比例尺。

如：2:1 为了计算方便，通常把放大比例尺写成( ):1。

图形的放大与缩小的特点是：形状相同，大小不同知识点一：比例尺的概念与分类例1：一幅图的比例尺是 ， 那么图上的1厘米表示实际距离（ ）；实际距离50千米在图上要画（ ）厘米。

把这个线段比例尺改写成数值比例尺是（ ）。

例2：在比例尺是1：4000000的地图上，图上距离1厘米表示实际距离（ ）千米。

也就是图上距离是实际距离的()1，实际距离是图上距离的（ ）倍。

知识点二：比例尺应用题例3：在一幅比例尺是1:3000000的地图上，甲乙两地的距离是7.5厘米，甲乙两地的实际距离是多少千米？例4：一幅地图的线段比例尺是：甲乙两城在这幅地图上相距18厘米，两城间的实际距离是多少千米？丙丁两城相距660千米，在这幅地图上两城之间的距离是多少厘米？知识点三：图形的放大与缩小例5：(1)将下面的平行四边形按3：1放 (2)将下面的三角形按1：2缩小一、填空题1、在一幅比例尺是1:10000000的地图上，量得北京与深圳之间的距离是26厘米。

苏科版数学九年级下册《6.1 图上距离与实际距离》教学设计4一. 教材分析《苏科版数学九年级下册》第六章第一节《图上距离与实际距离》的内容，主要让学生掌握比例尺的概念，以及如何将图上的距离转换为实际距离。

这一节内容是整个初中数学的重要部分，也是学生首次接触比例尺的知识，对于培养学生的空间想象能力和实际问题解决能力具有重要意义。

二. 学情分析九年级的学生已经具备了一定的空间想象能力和实际问题解决能力，但是对于比例尺的概念以及如何应用可能还比较模糊。

因此，在教学过程中，需要引导学生通过实际操作，理解比例尺的含义，并学会如何将图上的距离转换为实际距离。

三. 教学目标1.知识与技能：使学生掌握比例尺的概念，理解比例尺的应用，能够将图上的距离转换为实际距离。

2.过程与方法：通过实际操作，培养学生的空间想象能力和实际问题解决能力。

3.情感态度价值观：激发学生学习数学的兴趣，培养学生的探究精神和合作意识。

四. 教学重难点1.重点：比例尺的概念，以及如何将图上的距离转换为实际距离。

2.难点：比例尺的应用，以及如何将图上的距离转换为实际距离。

五. 教学方法采用“问题驱动”的教学方法，引导学生通过实际操作，理解比例尺的概念，并学会如何将图上的距离转换为实际距离。

同时，运用小组合作的学习方式，培养学生的团队协作能力和实际问题解决能力。

六. 教学准备1.教具准备：比例尺模型，实际距离模型，图上距离模型。

2.教学素材：相关例题，练习题。

七. 教学过程1.导入（5分钟）教师通过展示比例尺模型，引导学生思考比例尺的含义，激发学生的学习兴趣。

2.呈现（10分钟）教师通过PPT或者黑板，呈现比例尺的定义，解释比例尺的概念，让学生理解比例尺的含义。

3.操练（10分钟）教师给出一个实际距离模型，让学生通过图上距离模型，计算出实际距离。

学生分组进行操作，教师巡回指导。

4.巩固（10分钟）教师给出一些练习题，让学生独立完成，巩固比例尺的概念和应用。

苏科版数学九年级下册6.1《图上距离与实际距离》教学设计一. 教材分析《图上距离与实际距离》是苏科版数学九年级下册第六章第一节的内容。

本节课主要让学生学会在实际问题中，将图上的距离转换为实际距离，并理解比例尺的概念及其应用。

教材通过具体的例题和练习，帮助学生掌握图上距离与实际距离的转换方法，培养学生解决实际问题的能力。

二. 学情分析学生在学习本节课之前，已经掌握了相似多边形的性质和坐标与图形的变换等知识。

但是，对于比例尺的概念及其应用，部分学生可能还比较陌生。

因此，在教学过程中，教师需要关注学生的知识基础，针对性地进行教学。

三. 教学目标1.知识与技能目标：让学生理解比例尺的概念，学会将图上的距离转换为实际距离，并能运用比例尺解决实际问题。

2.过程与方法目标：通过合作交流、探究学习，培养学生解决问题的能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的团队合作精神。

四. 教学重难点1.重点：比例尺的概念及其应用。

2.难点：如何将图上的距离转换为实际距离，以及如何运用比例尺解决实际问题。

五. 教学方法1.采用问题驱动的教学方法，引导学生主动探究，发现规律。

2.利用多媒体辅助教学，直观展示比例尺的应用。

3.学生进行小组讨论，培养学生的团队合作精神。

4.注重启发式教学，让学生在思考中掌握知识。

六. 教学准备1.准备相关的教学课件和教学素材。

2.准备比例尺为1:1000的地图和尺子。

3.准备一些实际问题，让学生进行练习。

七. 教学过程1.导入（5分钟）利用多媒体展示一些与比例尺相关的图片，如地图、设计图等，引导学生思考：这些图上的距离与实际距离之间有什么关系？进而引入本节课的主题——图上距离与实际距离。

2.呈现（10分钟）教师展示比例尺为1:1000的地图和尺子，向学生讲解比例尺的概念，并演示如何将地图上的距离转换为实际距离。

同时，让学生进行实际操作，加深对比例尺的理解。

3.操练（10分钟）教师提出一些实际问题，让学生运用比例尺进行解答。

比例尺及比‎例尺缩放比例尺=图上距离/实际距离。

比例尺通常‎有三种表示‎方法。

（1）数字式，用数字的比‎例式或分数‎式表示比例‎尺的大小。

例如地图上‎1厘米代表‎实地距离5‎00千米，可写成：1∶50 000 000或写‎成：五千万分之‎一。

（2）线段式，在地图上画‎一条线段，并注明地图‎上1厘米所‎代表的实际‎距离。

（3）文字式，在地图上用‎文字直接写‎出地图上1‎厘米代表实‎地距离多少‎千米，如图上1厘‎米相当于地‎面距离10‎千米。

三种表示方‎法可以互换‎。

根据地图上‎的比例尺，可以量算图‎上两地之间‎的实地距离‎；根据两地的‎实际距离和‎比例尺，可计算两地‎的图上距离‎；根据两地的‎图上距离和‎实际距离，可以计算比‎例尺。

根据地图的‎用途，所表示地区‎范围的大小‎、图幅的大小‎和表示内容‎的详略等不‎同情况，制图选用的‎比例尺有大‎有小。

地图比例尺‎中的分子通‎常为1，分母越大，比例尺就越‎小。

通常比例尺‎大于二十万‎分之一的地‎图称为大比‎例尺地图；比例尺介于‎二十万分之‎一至一百万‎分之一之间‎的地图，称为中比例‎尺地图；比例尺小于‎一百万分之‎一的地图，称为小比例‎尺地图。

在同样图幅‎上，比例尺越大‎，地图所表示‎的范围越小‎，图内表示的‎内容越详细‎，精度越高；比例尺越小‎，地图上所表‎示的范围越‎大，反映的内容‎越简略，精确度越低‎。

地理课本和‎中学生使用‎的地图册中‎的地图，多数属于小‎比例尺地图‎。

比例尺缩放‎的计算将原比例尺‎放大到n倍‎;原比例Xn‎。

将原比例尺‎放大n倍;原比例X(n+1)。

将原比例尺‎缩小到1/n;原比例X1‎/n。

将原比例尺‎缩小1/n;原比例X(1-1/n)。

比例尺缩放‎后,原面积之比‎变为缩放倍‎数的平方。

1一支特种‎兵小分队，在方圆25‎平方千米的‎范围内执行‎任务，小分队指挥‎员所使用的‎地图，比例尺应当‎为A．1∶1，000，000 B．1∶500，000 C．1∶500 D．1∶10，0002某地图上‎，甲乙两地相‎距11.1厘米，且都位于北‎半球的同一‎条经线上，当夏至日太‎阳位于上中‎天时，测得甲地太‎阳高度为6‎0°，乙地为50‎°,那么该地图‎的比例尺是‎()A.1:24000‎000B.1:30000‎00C.1:50000‎0D.1:10000‎0003将1：10000‎的某幅地图‎，表达的范围‎不变，图幅放大为‎原图的四倍‎，则新图的比‎例尺是（）A．比例尺不变‎B.1：2000 C.1:5000 D.1:40000‎4将1/50000‎的比例尺缩‎小1/4，则新比例尺‎变为( )A.1：50000‎B.1：50000‎00C.1：66500‎D.1：20000‎005将1：10000‎000的地‎图比例尺放‎大到2倍后‎，则新比例尺‎是（）A.1：20000‎000B.1：50000‎00C.1：10000‎000D.1：20000‎001【解题思路】从表面上看‎，题目中没有‎直接提供图‎上距离和实‎际距离，这就需要从‎题目中进行‎挖掘。

比例尺实际距离公式
比例尺=图上距离÷实际距离，这个公式是计算比例尺时常用的公式，它可以
让我们更清楚地了解比例尺的实际意义。

在实际应用中，比例尺的计算公式可以简化为：比例尺=图上距离÷实际距离。

这个公式可以让我们根据地图上的距离和实际距离计算出比例尺，从而更好地理解地图的比例尺含义。

除了比例尺的计算公式外，我们还需要注意单位间的换算，以及在实际应用中要考虑的细节问题，如方向、千米和厘米的换算等。

这些细节问题可能会影响比例尺的计算和地图的使用效果。

因此，在计算比例尺时，我们应结合具体情况灵活应用相关公式。

比例尺怎么算一1比例尺计算1.图上距离÷实际距离=比例尺2.图上距离÷比例尺=实际距离3.比例尺×实际距离=图上距离2比例尺三种形式1.数字式：用数字的比例式或分数式表示比例尺的大小。

例如地图上1厘米代表实地距离500千米，可写成1∶50000000或写成：五千万分之一。

2.线段式，在地图上画一条线段，并注明地图上1厘米所代表的实际距离。

3.文字式，在地图上用文字直接写出地图上1厘米代表实地距离多少千米，如图上1厘米相当于地面距离10千米。

3地图比例尺表示图上距离比实际距离缩小（或放大）的程度，因此也叫缩尺。

如1∶10万，即图上1厘米长度相当于实地1000米。

严格讲，只有在表示小范围的大比例尺地图上，由于不考虑地球的曲率，全图比例尺才是一致的。

通常绘注在地图上的比例尺称为主比例尺。

在地图上，只有某些线或点符合主比例尺。

比例尺与地图内容的详细程度和精度有关。

二比例尺=图上距离/实际距离。

比例尺的概念：比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比。

按照比例尺概念，比例尺的算式为:比例尺=图上距离/实际距离。

比例尺的特点:比例尺实际上是一个“比”；比例尺是图上距离与实际距离的“比”；图上距离和实际距离的单位是统一的（即换算成相同单位再比），所以比例尺没有单位（单位统一被约分了）；比例尺的前项一般为1。

比例尺的换算方法：（1）长度单位换算公式：1公里=1千米。

1000米=1千米。

1米=10分米=100厘米=1000毫米。

1分米=10厘米=100毫米。

1厘米=10毫米。

（2）比例尺的换算：举例说明:“图上一厘米代表实际1公里，比例尺是多少？”解析:长度单位换算公式是孩子原来就掌握的知识，因为比例尺必须统一单位，只需要按长度单位换算公式，将图上距离和实际距离的单位换算成相同单位，然后统一代入比例尺算式，比例尺=1厘米/1公里=1厘米/100000厘米=1/100000。