1平面机构的自由度和速度分析

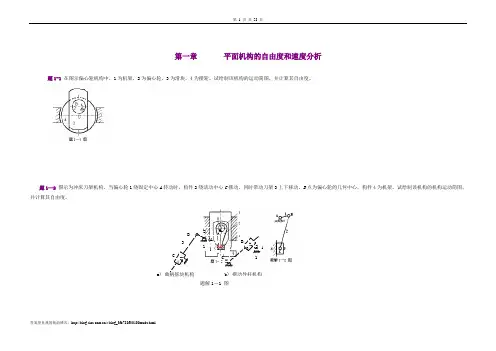
第一章平面机构的自由度和速度分析题1-1在图示偏心轮机构中，1为机架，2为偏心轮，3为滑块，4为摆轮。

试绘制该机构的运动简图，并计算其自由度。

题1—2图示为冲床刀架机构，当偏心轮1绕固定中心A转动时，构件2绕活动中心C摆动，同时带动刀架3上下移动。

B点为偏心轮的几何中心，构件4为机架。

试绘制该机构的机构运动简图，并计算其自由度。

题1—3计算题1－3图a）与图b）所示机构的自由度（若有复合铰链，局部自由度或虚约束应明确指出）。

题1－3图a）题1－3图b）题1—4计算题1—4图a、图b所示机构的自由度（若有复合铰链，局部自由度或虚约束应明确指出），并判断机构的运动是否确定，图中画有箭头的构件为原动件。

题1—5 计算题1—5图所示机构的自由度（若有复合铰链，局部自由度或虚约束应明确指出）,并标出原动件。

题1—5图 题解1—5图题1-6 求出图示的各四杆机构在图示位置时的全部瞬心。

第二章 连杆机构题2-1在图示铰链四杆机构中，已知 l BC =100mm ，l CD =70mm ，l AD =60mm ，AD 为机架。

试问：（1）若此机构为曲柄摇杆机构，且AB 为曲柄，求l AB 的最大值；（2）若此机构为双曲柄机构，求l AB 最小值； （3）若此机构为双摇杆机构，求l AB 的取值范围。

题2-2 如图所示的曲柄滑块机构： （1）曲柄为主动件，滑块朝右运动为工作 行程，试确定曲柄的合理转向，并简述其理由；（2）当曲柄为主动件时，画出极位夹角θ，最小传动角g min ； （3）设滑块为主动件，试用作图法确定该机构的死点位置 。

D题2-1图题2-3图示为偏置曲柄滑块机构，当以曲柄为原动件时，在图中标出传动角的位置，并给出机构传动角的表达式，分析机构的各参数对最小传动角的影响。

题2-4设计一曲柄摇杆机构，已知机构的摇杆DC长度为150mm，摇杆的两极限位置的夹角为45°，行程速比系数K=1.5，机架长度取90mm。

平面机构的自由度与运动分析一、平面机构的自由度平面机构是指机构中的构件只能在一个平面内运动的机构，它由多个连接杆、转动副和滑动副组成。

平面机构的自由度是指机构中能够独立变换位置的最小的连接杆数目，也可以理解为机构中独立的变量的数量。

对于平面机构，其自由度可以通过以下公式计算：自由度=3n-2j-h其中，n表示连接杆的数量，j表示驱动链的数量，h表示外部约束的数量。

根据上述公式可以看出，自由度与平面机构中连接杆的数量和驱动链和外部约束的数量有关。

连接杆的数量越多，机构的自由度就越大，可以实现更复杂的运动。

驱动链的数量越多，机构中的动力驱动器越多，自由度就越小，机构的运动变得更加确定。

外部约束的数量越多，机构中的约束条件就越多，自由度就越小，机构的运动也会变得更加确定。

二、平面机构的运动分析1.闭合链和链架分析：首先需要确定机构中的闭合链和链架，闭合链是指机构中连接杆形成一个封闭的回路，闭合链中的连接杆数目应该为n 或n-1，n是机构中的连接杆数量。

链架是指机构中的连接杆形成一个开放的链路。

通过分析闭合链和链架中的链接关系和约束条件，可以确定机构中构件的位置和运动方式。

2.位置和速度分析：根据机构的连接杆的长度和角度，可以通过几何方法或代数方法确定机构中构件的位置和速度分量。

通过分析连接杆的长度和角度的变化规律，可以推导出机构中构件的位置和速度随时间的变化关系。

3.加速度和动力学分析：根据机构中各个构件的位置和速度，可以通过几何方法或动力学方法计算构件的加速度和动力学特性。

通过分析机构中构件的加速度和动力学特性，可以确定机构中构件的运动稳定性和质量分布。

4.动力分析：对于需要携带负载或进行力学传动的机构，需要进行动力学分析，确定机构中各个构件的受力和承载能力。

通过分析机构中构件的受力情况，可以确定机构的设计参数和强度要求。

总结起来，平面机构的自由度与运动分析是确定机构中构件位置和运动状态的重要方法，通过分析机构中的闭合链和链架、构件的位置和速度、加速度和动力学特性，可以确定机构的运动方式和特性，为机构的设计和优化提供依据。

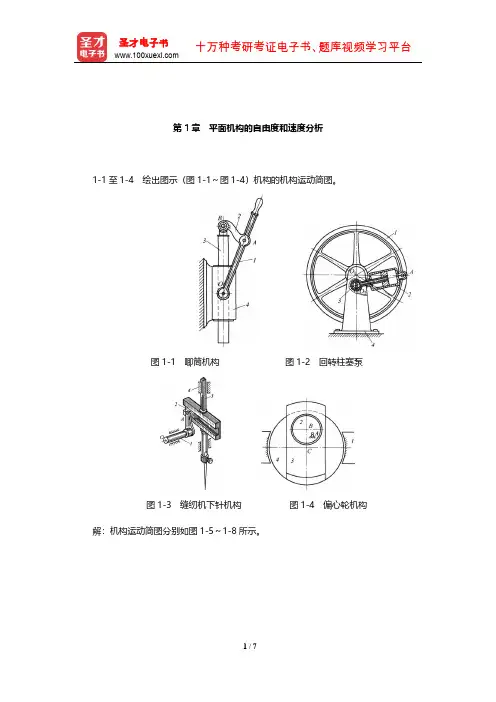
第1章平面机构的自由度和速度分析1-1至1-4 绘出图示（图1-1～图1-4）机构的机构运动简图。

图1-1 唧筒机构图1-2 回转柱塞泵图1-3 缝纫机下针机构图1-4 偏心轮机构解：机构运动简图分别如图1-5～1-8所示。

1-5至1-12 指出（图1-9～图1-16）机构运动简图中的复合铰链、局部自由度和虚约束，计算各机构的自由度。

图1-9 平炉渣口堵塞机构图1-10 锯木机机构图1-11 加药泵加药机构图1-12 测量仪表机构图1-13 缝纫机送布机构图1-14 冲压机构图1-15 差动轮系 图1-16 机械手解：图1-9 滚子处为局部自由度，。

图1-10 滚子处为局部自由度，。

图1-11。

图1-12。

图1-13 滚子处为局部自由度，。

图1-14 滚子处为局部自由度，右方三杆铰接处为复合铰链，下方两导程槽之一为虚约束，。

图1-15 最下方齿轮与机架，杆组成复合铰链，。

图1-16 3233233L H F n P P =--=⨯-⨯=。

1-13 求出图1-17导杆机构的全部瞬心和构件1、3的角速比。

图1-17 导杆机构解：该导杆机构的全部瞬心如图1-18所示。

由1141333413P P P P ωω=可得，杆件1、3的角速度比：3413131413P P P P ωω=。

1-14 求出图1-19正切机构的全部瞬心。

设1ω＝10 rad ／s ，求构件3的速度3ν。

图1-19 正切机构解：该正切机构的全部瞬心如图1-20所示。

由114133P P v ω=可得，构件3的速度：311413102002000v P P ω==⨯=。

1-15 图1-21所示为摩擦行星传动机构，设行星轮2与构件1、4保持纯滚动接触，图试用瞬心法求轮1与轮2的角速比1ω/2ω。

图1-21 摩擦行星传动机构解：确定轮1、轮2和机架4三个构件的三个瞬心121424P P P 、、，如图1-22所示。

由于在行星轮2和构件1的瞬心12P 处，有12v v =，即11222r r ωω=⋅ 因此，轮1和轮2的角速比12212r r ωω=。

第1章平面机构的自由度和速度分析1.1复习笔记【通关提要】本章是本书的基础章节之一，主要介绍了平面机构自由度的计算和平面机构的速度分析。

学习时需要掌握平面机构运动简图的绘制、自由度的计算和速度瞬心的应用等内容。

本章主要以选择题、填空题和计算题的形式考查，复习时需把握其具体内容，重点记忆。

【重点难点归纳】一、运动副及其分类（见表1-1-1）表1-1-1运动副及其分类二、平面机构运动简图机构运动简图指用简单线条和符号来表示构件和运动副，并按比例定出各运动副的位置，来表明机构间相对运动关系的简化图形。

1．机构中运动副表示方法机构运动简图中的运动副的表示方法如图1-1-1所示。

图1-1-1平面运动副的表示方法2．构件的表示方法构件的表示方法如图1-1-2所示。

图1-1-2构件的表示方法3．机构中构件的分类（见表1-1-2）表1-1-2机构中构件的分类三、平面机构的自由度活动构件的自由度总数减去运动副引入的约束总数称为机构自由度，以F表示。

1．平面机构自由度计算公式F＝3n－2P L－P H式中，n为机构中活动构件的数目；P L为低副的个数；P H为高副的个数。

机构具有确定运动的条件是：机构的自由度F＞0且F等于原动件数目。

2．计算平面机构自由度的注意事项（见表1-1-3）表1-1-3计算平面机构自由度的注意事项四、速度瞬心及其在机构速度分析上的应用（见表1-1-4）表1-1-4速度瞬心及其应用1.2课后习题详解1-1至1-4绘出图示（图1-2-1～图1-2-4）的机构运动简图。

图1-2-1唧筒机构图1-2-2回转柱塞泵图1-2-3缝纫机下针机构图1-2-4偏心轮机构答：机构运动简图分别如图1-2-5～图1-2-8所示。

1-5至1-13指出（图1-2-9～图1-2-17）机构运动简图中的复合铰链、局部自由度和虚约束，计算各机构的自由度。

解：（1）图1-2-9所示机构的自由度为F＝3n－2P L－P H＝3×7－2×10－0＝1（2）图1-2-10中，滚子1处有一个局部自由度，则该机构的自由度为F＝3n－2P L－P H＝3×6－2×9－0＝0（3）图1-2-11中，滚子1处有一个局部自由度，则该机构的自由度为F＝3n－2P L－P H＝3×8－2×11－1＝1（4）图1-2-12所示机构的自由度为F＝3n－2P L－P H＝3×8－2×11－0＝2（5）图1-2-13所示机构的自由度为F＝3n－2P L－P H＝3×6－2×8－1＝1（6）图1-2-14中，滚子1处有一个局部自由度，则该机构的自由度为F＝3n－2P L－P H＝3×4－2×5－1＝1（7）图1-2-15中，滚子1处有一个局部自由度，A处为三个构件汇交的复合铰链，移动副B、B′的其中之一为虚约束。

01平面机构的自由度和速度分析平面机构是最基本的机械结构之一，广泛应用于机械工程中。

对于平面机构的自由度和速度分析是研究机构运动特性和设计优化的重要内容之一、本文将对平面机构的自由度和速度分析进行详细阐述。

一、平面机构的自由度分析自由度是指机构中运动自由的独立参数个数，即描述机构运动特性的最小信息单位。

对于平面机构而言，其自由度可以通过分析机构中的运动副个数进行计算。

1.单刚性连杆机构的自由度分析单刚性连杆机构是最简单的平面机构，由若干个刚性连杆组成，连接点上的关节用铰链连接。

在单刚性连杆机构中，关节的个数可以通过Euler公式计算：f = 3n - m - 2，其中f为机构的自由度，n为连杆数目，m为连接关节的个数。

根据Euler公式，当机构中的连杆数目和连接关节的个数已知时，就可以得到机构的自由度。

2.多刚性连杆机构的自由度分析多刚性连杆机构是由多个单刚性连杆机构组成的机构。

通过分析机构中的连杆数目和连接关节的个数，同样可以得到机构的自由度。

与单刚性连杆机构相似，多刚性连杆机构的自由度可以通过Euler公式进行计算。

3.灵活性连杆机构的自由度分析灵活性连杆机构是由柔性杆件构成的机构。

由于柔性杆件的存在，机构的自由度在一定程度上受到限制。

灵活性连杆机构的自由度分析可以通过变分原理进行研究，将柔性杆件的变形引入到计算中，得到机构的自由度。

二、平面机构的速度分析平面机构的速度分析是指研究机构中各点的速度和加速度特性。

根据机构的不同类型和运动特性，速度分析可以采用不同的方法。

1.单刚性连杆机构的速度分析对于单刚性连杆机构，速度分析可以通过运动相对性原理进行计算。

根据运动相对性原理，机构中各点的速度相对于机构中其中一固定点的速度可以通过对机构进行平移和旋转变换得到。

通过变换矩阵的乘积，可以得到机构中各点的速度。

2.多刚性连杆机构的速度分析多刚性连杆机构的速度分析比单刚性连杆机构的速度分析复杂一些。

根据机构的运动特性和几何约束条件，可以通过求解速度方程组得到机构中各点的速度。