2013年北京理工大学附中高考数学二轮复习精品训练平面向量

北京理工大学附中2013届高考数学二轮复习精品训练：选考内容本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．点先后通过矩阵⎪⎪⎭⎫ ⎝⎛=210011M 和⎪⎪⎭⎫ ⎝⎛=310012M 的变换效果相当于另一变换是( ) A ． ⎪⎪⎪⎪⎭⎫ ⎝⎛210031 B ． ⎪⎪⎪⎪⎭⎫ ⎝⎛210061 C ． ⎪⎪⎪⎪⎭⎫ ⎝⎛610021 D ． ⎪⎪⎭⎫ ⎝⎛61001 【答案】D2．在极坐标系中与点4(6,)3A π重合的点是( ) A ．(6,)3π B ．7(6,)3π C ．(6,)3π- D ．2(6,)3π- 【答案】C3．不等式3≤l5 - 2xl<9的解集是( )A ．（一∞，-2)U(7,+co)B ．[1,4]C ．[-2,1】U 【4,7】D ． (2,1][4,7)-【答案】D 4．直线12x ty =-⎧⎪⎨=-⎪⎩(t 为参数)的倾斜角为( ) A ．3π B ．6π C ．23π D ．56π 【答案】A5．若x a h -<，y a h -<，则下面不等式中一定成立的是( )A ．x y h -<B ．x y h -> C ．2x y h ->D ．2x y h -<【答案】D6．直角坐标系xoy 中，以原点为极点，x 轴的正半轴为极轴建极坐标系，设点A,B 分别在曲线13cos :sin x C y θθ=+⎧⎨=⎩ (θ为参数）和曲线2:1C ρ=上，则AB 的最小值为( ) A ．1B ．2C ．3D ．4【答案】A7．若点P(3,m)在以点F 为焦点的抛物线244x t y t ⎧=,⎨=⎩ (t 为参数)上,则|PF|等于( )A ．2B ．3C ．4D ．5【答案】C8．直线)(20cos 20sin 3为参数t t y t x ⎪⎩⎪⎨⎧-=+=︒︒的倾斜角是( )A ．︒20B ． ︒70C ． ︒110D ． ︒160【答案】C9．使|x －4|+|x －5|＜a 有实数解的a 为( )A ．a ＞1B ．1＜a ＜9C ．a ＞1D ．a ≥1【答案】A10．如图，边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D '''，图中阴影部分的面积为( )A．1 BC．1 D ．12【答案】A11．已知关于x y 、的二元一次线性方程组的增广矩阵为111222a b c a b c ⎛⎫⎪⎝⎭，记121212(,),(,),(,)a a a b b b c c c ===，则此线性方程组有无穷多组解的充要条件是( )A ． 0a b c ++=B ． a b c 、、两两平行．C ． a b //．D ． a b c 、、方向都相同．【答案】B12．已知x,y ∈R 且122=+y x ，a,b ∈R 为常数，22222222y a x b y b x a t +++=则( )A ．t 有最大值也有最小值B ．t 有最大值无最小值C ．t 有最小值无最大值D ．t 既无最大值也无最小值【答案】A第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．与曲线401cos πθθρ==+关于直线对称的曲线的极坐标方程是____________【答案】01sin =+θρ14．若关于x 的不等式a x ax 2|1|2++-＜0的解集为∅，则实数a 的取值范围为【答案】)+∞ 15．不等式|2||3|--+x x ≥3的解集为____________.【答案】}1|{≥x x16．函数x x x xe e e e xf --+=11)(在闭区间]21,21[-上的最小值为. 【答案】21e -三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．如下图，AB 、CD 是圆的两条平行弦，BE//AC ，BE 交CD 于E 、交圆于F ，过A 点的切线交DC 的延长线于P ，PC=ED=1，PA=2．(I ）求AC 的长；（II ）求证：BE ＝EF ．【答案】（I ）1,2,2==⋅=PC PA PD PC PA ，4=∴PD ，又2,1=∴==CE ED PC ，,,CAB PCA CBA PAC ∠=∠∠=∠CBA PAC ∆∆∴∽，ABAC AC PC =∴， 22=⋅=∴AB PC AC ，2=∴AC(II ） 2==AC BE ，2=CE ，而EF BE ED CE ⋅=⋅，2212=⋅=∴EF ，BE EF =∴．18．已知函数52)(---=x x x f (1) 证明:3)(3≤≤-x f(2) 求不等式158)(2+-≥x x x f 的解集.【答案】（I ）3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时所以3() 3.f x -≤≤(II ）由（I ）可知，当22,()815x f x x x ≤≥-+时的解集为空集；当225,()815{|55}x f x x x x x <<≥-+-≤<时的解集为； 当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上，不等式2()815{|56}.f x x x x x ≥-+-≤≤的解集为 19．在极坐标系中，直线l 的极坐标方程为()3R πθρ=∈，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，曲线C 的参数方程为2cos ,1cos 2,x y αα=⎧⎨=+⎩（α为参数），求直线l 与曲线C 的交点P 的直角坐标．【答案】因为直线l 的极坐标方程为=()3θρπ∈R ，所以直线l 的普通方程为y =，①又因为曲线C 的参数方程为2cos ,1cos 2x y αα=⎧⎨=+⎩(α为参数)， 所以曲线C 的直角坐标方程为212y x =([2,2])x ∈-，②联立①②解方程组得0,0x y =⎧⎨=⎩ 或 6.x y ⎧=⎪⎨=⎪⎩根据x 的范围应舍去6,x y ⎧=⎪⎨=⎪⎩故P 点的直角坐标为(0，0).20．在极坐标系中，圆C 的方程为)4ρθπ=+，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为,12x t y t =⎧⎨=+⎩（t 为参数），判断直线l 和圆C 的位置关系． 【答案】消去参数t ，得直线l 的直角坐标方程为21y x =+；)4πρθ=+即2(sin cos )ρθθ=+， 两边同乘以ρ得22(sin cos )ρρθρθ=+，得⊙C 的直角坐标方程为：22(1)(1)2x x -+-=,圆心C 到直线l 的距离d ==<， 所以直线l 和⊙C 相交． 21．已知函数f （x ）＝|x －2|，g （x ）＝－|x ＋3|＋m ．(Ⅰ）解关于x 的不等式f （x ）＋a －1>0（a ∈R ）；(Ⅱ）若函数f （x ）的图象恒在函数g （x ）图象的上方，求m 的取值范围．【答案】（1）不等式f （x ）＋a －1>0，即|x －2|＋a －1>0，当a ＝1时，解集为x ≠2，即（－∞，2）∪（2，＋∞）；当a>1时，解集为全体实数R ；当a<1时，∵|x －2|>1－a ，∴x －2>1－a 或x －2<a －1，∴x>3－a 或x<a ＋1，故解集为（－∞，a ＋1）∪（3－a ，＋∞）．(2）f （x ）的图象恒在函数g （x ）图象的上方，即为|x －2|>－|x ＋3|＋m 对任意实数x 恒成立，即|x －2|＋|x ＋3|>m 恒成立．又对任意实数x 恒有|x －2|＋|x ＋3|≥|（x －2）－（x ＋3）|＝5，于是得m<5，即m 的取值范围是（－∞，5）．22．已知n m ,是正数，证明：2233n m mn n m +≥+。

北京理工大学附中2013届高考数学二轮复习精品训练：数列本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知等比数列{n a }的前n 项和为n S ,且317S a =，则数列{}n a 的公比q 的值为( )A ．2B ．3C ．2或-3D ．2或3【答案】C2．等差数列{}n a 中，652,30,a S ==则8S =( )A ．31B ．32C ．33D ．34【答案】B3．“公差为0的等差数列是等比数列”；“公比为21的等比数列一定是递减数列”；“a,b, c 三数成等比数列的充要条件是b 2=ac ”；“a,b,c 三数成等差数列的充要条件是2b=a+c ”，以上四个命题中，正确的有( ) A ．1个 B ．2个C ．3个D ．4个【答案】A4．数列{}n a 中，352,1,a a ==如果数列11n a +⎧⎫⎨⎬⎩⎭是等差数列，则11a =( )A ． 113-B ． 17-C ．0D ．111【答案】C5．设是等差数列的前项和，若则( )A ．B ．C ．D ．【答案】A6．设n S 是公差不为0的等差数列{n a ｝的前n 项和，且124,,S S S 成等比数列，则21a a 等于( ) A ．5 B ．4C ．3D ．2【答案】C7．数列{}n a 是首项41=a 的等比数列，且14a ，5a ，32a -成等差数列，则其公比为( )A ．1B ． 1-C ． 1或1-D ．2【答案】C8．设等比数列{}n a 的公比为q ，前n 项和n S ，若1n S +，n S ，2n S +成等差数列，则公比q 为( )A ．2q =-B ．2q =或1q =-C ．2q =-或1q =D ．1q =【答案】A9．已知{}n a 是等比数列，41252==a a ，，则公比q =( ) A ．21-B ．2-C ．2D ．21【答案】D10．如果－1,a,b,c,－9成等比数列, 那么( )A ． b=3,ac=9B ． b=－3,ac=9C ． b=3,ac=－9D ．b=－3,ac=－9【答案】B11．已知等比数列{}n a 中，各项都是正数，且2312,21,a a a 成等差数列，则8967a a a a ++等于( ) A ．21+ B ． 21- C ． 223+ D ． 223-【答案】C 12．已知()x x x f +=2，则数列()()*1N n n f ∈⎭⎬⎫⎩⎨⎧的前n 项和为( )A ．1+n n B ．21++n n C ．nn 1- D ．11+n 【答案】A第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．设f(x)=221+x ,利用课本中推导等差数列前n 项和的公式的方法,可求得f(－8)+f(－7)+…+f(0)+…+f(8)+f(9)的值为___________________.14．若等比数列{}n a 满足：151,8a a ==，则3a = ；【答案】15．等比数列a+log 23,a+log 43,a+log 83的公比是____________. 【答案】31 16．已知各项均为正数的等比数列{}n a 的前n 项和为4237,3,2,n S S S a a ==若则= 。

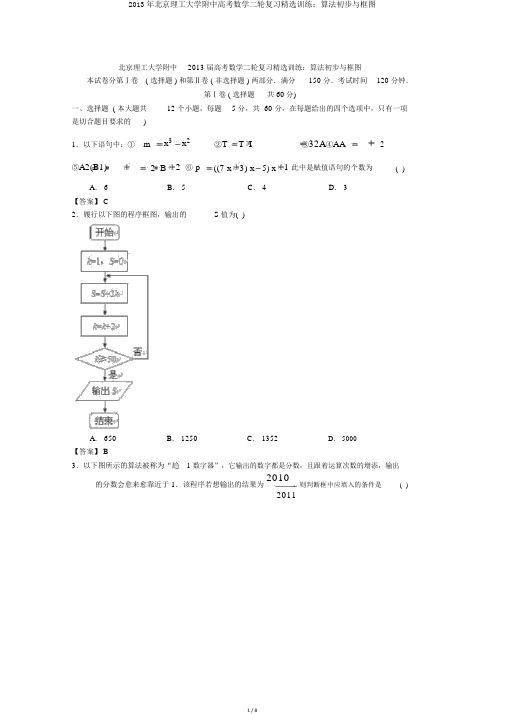
北京理工大学附中2013 届高考数学二轮复习精选训练：算法初步与框图本试卷分第Ⅰ卷( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分．满分150 分．考试时间120 分钟．第Ⅰ卷 ( 选择题共60分)一、选择题 ( 本大题共12 个小题，每题 5 分，共 60 分，在每题给出的四个选项中，只有一项是切合题目要求的)1．以下语句中：①m x3 x2 ②T T I ③32A④AA 2⑤A2(B1) 2 B 2 ⑥ p ((7 x 3) x 5) x 1 此中是赋值语句的个数为( )A． 6 B． 5 C． 4 D． 3【答案】 C2．履行以下图的程序框图，输出的S值为( )A． 650B． 1250C． 1352D． 5000【答案】 B3．以下图所示的算法被称为“趋 1 数字器”，它输出的数字都是分数，且跟着运算次数的增添，输出的分数会愈来愈靠近于1．该程序若想输出的结果为2010，则判断框中应填入的条件是( ) 2011A． i<2011B． i<2010C． i<2009？D． i<2008 ？【答案】 A4．以下程序运转的结果是( )A． 1,2,3B． 2,3,1C． 2,3,2D． 3,2,1【答案】 C5．任何一个算法都离不开的基本构造为( )A．逻辑构造B．条件构造C．循环构造D．次序构造【答案】 D6．赋值语句“x＝ x ＋ 1”的正确解说为( )A． x 的值与 x＋ 1 的值可能相等B．将本来x 的值加上 1 后，获得的值替代本来x 的值C．这是一个错误的语句D．此表达式经过移项后，可与x＝ x－ 1 功能同样【答案】 B7．以下语句中是算法的个数为( )①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎；②兼顾法中“烧水沏茶”的故事；③丈量某棵树的高度，判断其是不是大树；④已知三角形的一部分边长和角，借助正余弦定理求得节余的边角，再利用三角形的面积公式求出该三角形的面积。

北京理工大学附中2013届高考数学二轮复习精品训练：选考内容本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．点先后通过矩阵⎪⎪⎭⎫ ⎝⎛=210011M 和⎪⎪⎭⎫ ⎝⎛=310012M 的变换效果相当于另一变换是( )A ． ⎪⎪⎪⎪⎭⎫ ⎝⎛210031 B ． ⎪⎪⎪⎪⎭⎫⎝⎛210061 C ． ⎪⎪⎪⎪⎭⎫⎝⎛610021 D ． ⎪⎪⎭⎫⎝⎛61001【答案】D2．在极坐标系中与点4(6,)3A π重合的点是( )A ．(6,)3πB ．7(6,)3πC ．(6,)3π- D ．2(6,)3π-【答案】C3．不等式3≤l5 - 2xl<9的解集是( )A ．（一∞，-2)U(7,+co)B ．[1,4]C ．[-2,1】U 【4,7】D ． (2,1][4,7)-U【答案】D4．直线123x ty t =-⎧⎪⎨=--⎪⎩(t 为参数)的倾斜角为( )A ．3πB ．6πC ．23πD ．56π【答案】A5．若x a h -<，y a h -<，则下面不等式中一定成立的是( )A ．x y h -<B ．x y h ->C ．2x y h ->D ．2x y h -<【答案】D6．直角坐标系xoy 中，以原点为极点，x 轴的正半轴为极轴建极坐标系，设点A,B 分别在曲线13cos :sin x C y θθ=+⎧⎨=⎩ (θ为参数）和曲线2:1C ρ=上，则AB 的最小值为( )A ．1B ．2C ．3D ．4【答案】A7．若点P(3,m)在以点F 为焦点的抛物线244x t y t ⎧=,⎨=⎩(t 为参数)上,则|PF|等于( ) A ．2B ．3C ．4D ．5【答案】C 8．直线)(20cos 20sin 3为参数t t y t x ⎪⎩⎪⎨⎧-=+=︒︒的倾斜角是( ) A ．︒20 B ． ︒70 C ． ︒110 D ． ︒160【答案】C9．使|x －4|+|x －5|＜a 有实数解的a 为( )A ．a ＞1B ．1＜a ＜9C ．a ＞1D ．a ≥1【答案】A 10．如图，边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D '''，图中阴影部分的面积为( )A ．313-B ．33C ．314-D ．12【答案】A11．已知关于x y 、的二元一次线性方程组的增广矩阵为111222a b c a b c ⎛⎫ ⎪⎝⎭，记121212(,),(,),(,)a a a b b b c c c ===r r r ，则此线性方程组有无穷多组解的充要条件是( ) A ． 0a b c ++=r r r r B ． a b c r r r 、、两两平行． C ． a b r r //． D ． a b c r r r 、、方向都相同． 【答案】B12．已知x,y ∈R 且122=+y x ，a,b ∈R 为常数，22222222y a x b y b x a t +++=则( )A ．t 有最大值也有最小值B ．t 有最大值无最小值C ．t 有最小值无最大值D ．t 既无最大值也无最小值【答案】A 第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．与曲线401cos πθθρ==+关于直线对称的曲线的极坐标方程是____________【答案】01sin =+θρ14．若关于x 的不等式a x ax 2|1|2++-＜0的解集为∅，则实数a 的取值范围为 【答案】31[,)4++∞ 15．不等式|2||3|--+x x ≥3的解集为____________.【答案】}1|{≥x x16．函数x x x xe e e e xf --+=11)(在闭区间]21,21[-上的最小值为 . 【答案】21e -三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．如下图，AB 、CD 是圆的两条平行弦，BE//AC ，BE 交CD 于E 、交圆于F ，过A 点的切线交DC 的延长线于P ，PC=ED=1，PA=2．(I ）求AC 的长；（II ）求证：BE ＝EF ．【答案】（I ）1,2,2==⋅=PC PA PD PC PA Θ，4=∴PD ，又2,1=∴==CE ED PC Θ，,,CAB PCA CBA PAC ∠=∠∠=∠ΘCBA PAC ∆∆∴∽，ABAC AC PC =∴， 22=⋅=∴AB PC AC ，2=∴AC(II ）Θ2==AC BE ，2=CE ，而EF BE ED CE ⋅=⋅，2212=⋅=∴EF ，BE EF =∴．18．已知函数52)(---=x x x f (1) 证明:3)(3≤≤-x f(2) 求不等式158)(2+-≥x x x f 的解集.【答案】（I ）3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时所以3() 3.f x -≤≤ (I I ）由（I ）可知，当22,()815x f x x x ≤≥-+时的解集为空集；当225,()815{|535}x f x x x x x <<≥-+-≤<时的解集为；当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上，不等式2()815{|536}.f x x x x x ≥-+-≤≤的解集为19．在极坐标系中，直线l 的极坐标方程为()3R πθρ=∈，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，曲线C 的参数方程为2cos ,1cos 2,x y αα=⎧⎨=+⎩（α为参数），求直线l 与曲线C 的交点P 的直角坐标． 【答案】因为直线l 的极坐标方程为=()3θρπ∈R ， 所以直线l 的普通方程为3y x =，①又因为曲线C 的参数方程为2cos ,1cos 2x y αα=⎧⎨=+⎩(α为参数)， 所以曲线C 的直角坐标方程为212y x =([2,2])x ∈-，② 联立①②解方程组得0,0x y =⎧⎨=⎩ 或3,6.x y ⎧=⎪⎨=⎪⎩根据x 的范围应舍去3,6,x y ⎧=⎪⎨=⎪⎩ 故P 点的直角坐标为(0，0).20．在极坐标系中，圆C 的方程为22)4ρθπ=+，以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为,12x t y t=⎧⎨=+⎩（t 为参数），判断直线l 和圆C 的位置关系． 【答案】消去参数t ，得直线l 的直角坐标方程为21y x =+；22(sin )4πρθ=+即2(sin cos )ρθθ=+， 两边同乘以ρ得22(sin cos )ρρθρθ=+，得⊙C 的直角坐标方程为：22(1)(1)2x x -+-=,圆心C 到直线l 的距离2225221d ==<+， 所以直线l 和⊙C 相交．21．已知函数f （x ）＝|x －2|，g （x ）＝－|x ＋3|＋m ．(Ⅰ）解关于x 的不等式f （x ）＋a －1>0（a ∈R ）；(Ⅱ）若函数f （x ）的图象恒在函数g （x ）图象的上方，求m 的取值范围．【答案】（1）不等式f （x ）＋a －1>0，即|x －2|＋a －1>0，当a ＝1时，解集为x ≠2，即（－∞，2）∪（2，＋∞）；当a>1时，解集为全体实数R ；当a<1时，∵|x －2|>1－a ，∴x －2>1－a 或x －2<a －1，∴x>3－a 或x<a ＋1，故解集为（－∞，a ＋1）∪（3－a ，＋∞）．(2）f （x ）的图象恒在函数g （x ）图象的上方，即为|x －2|>－|x ＋3|＋m 对任意实数x 恒成立，即|x －2|＋|x ＋3|>m 恒成立．又对任意实数x 恒有|x －2|＋|x ＋3|≥|（x －2）－（x ＋3）|＝5，于是得m<5，即m 的取值范围是（－∞，5）．22．已知n m ,是正数，证明：2233n m mn n m +≥+。

北京理工大学附中2013届高考数学二轮复习精品训练：集合与逻辑 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．总分值150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每题5分，共60分，在每题给出的四个选项中，只有一项是符合题目要求的)1．集合}5,4,3,2,1,0{=S ，A 是S 的一个子集，当A x ∈时，假设有A x ∉-1，且A x ∉+1，则称x 为A 的一个“孤立元素”，那么S 中无“孤立元素”的4个元素的子集A 的个数是( )A ．4B ．5C ．6D ．7【答案】C2．假设集合{}0,1,2A =，则集合A 的子集共有 ( )A ．3个B ．6个C ．7个D ．8个【答案】D 3．设全集N M C N M U U )(},5,4,3{},5,3,1{},5,4,3,2,1{则集合集合集合===等于( )A ．{4}B ．{2，3，4，5}C ．{1，3，4，5}D ．φ 【答案】A4．命题：∃x 0∈R ，x 20+2x 0+2≤0，该命题的否认是( )A ．∃x 0∈R ，x 20+2x 0+2≥0B ．∀x ∈R ，x 2+2x+2＞0C ．∀x ∈R ，x 2+2x+2≤0D ．假设x 20+2x 0+2≤0，则∃x 0∈R【答案】B5．在空间中，“两条直线没有公共点”是“这两条直线平行的” ( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B6．已知命题p ：m 、n 为直线，α为平面，假设m ∥n ，α⊂n ，则m ∥α；命题q ：假设a ＞b ，则ac ＞bc ，则以下命题为真命题的是( ) A ． p 或q B ． ⌝p 或q C ． ⌝p 且qD ． p 且q【答案】B7．给出以下命题： (1〕“假设1=xy ，则y x ,互为倒数”的逆命题；〔2〕“面积相等的三角形全等”的否命题；(3〕“假设1≤m ，则022=+-m x x 有实根”的逆否命题；(4〕“假设B B A = ，则B A ⊆”的逆否命题.其中为真命题的是( )A ．(1)(2)B ．(2)(3)C ．(1)(2)(3)D ．(3)(4)【答案】C8．已知甲：x ≥0 , 乙：|x-1|<1．则甲是乙的( )A ．必要非充分条件B ．充分非必要条件C ．即不必要也不充分条件D ．充要分条件【答案】A9．设0＜x ＜2π，则“x sin 2x ＜1”是“x sinx ＜1”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件 【答案】B 10．在ABC ∆中“ 30=A ”是“21=SinA ”的( ) A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 11．已知集合{}Z m m x x A ∈-==,12|，{}Z n n x x B ∈==,2|，且A x x ∈21,，B x ∈3，则以下判断不正确的选项是( )A ．A x x ∈⋅21B ．B x x ∈⋅32C ．B x x ∈+21D ．A x x x ∈++321 【答案】D12．“1＜a ＜2”是“对任意的正数x ，2a x x +≥2”的( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A 第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每题5分，共20分，把正确答案填在题中横线上)13．0x ∃<，使得2()lg(21)0f x x x =--≥的否认形式是 .【答案】0x ∀<，有2()lg(21)0f x x x =--<。

4、1 课后测试1. 已知正方形ABCD 的边长为1,AB = a ,=c ,则|a +b +c |=( ) C. 2 D. 222. 设四边形ABCD ，有DC =12AB ,且|AD |=|BC |,则此四边形是( ) A. 等腰梯形 B. 平行四边形 C. 正方形 D. 长方形3. 设a ，b 是任意的两个向量，λ∈R ，给出下面四个结论：①若a 与b 共线，则b ＝λa ;②若b ＝-λa ,则a 与b 共线; ③若a ＝λb ,则a 与b 共线;④当b ≠0时, a 与b 共线的充要条件是有且只有一个实数λ＝λ1,使得a ＝λ1b .其中正确的结论有( ) A. ①② B. ①③ C. ①③④ D. ②③④4. (2011·广州模拟）已知点O ，N 在△ABC 所在平面内，且|OA |=|OB |=|OC |，NA +NB +NC =0,则点O ，N 依次是△ABC 的（ ）A. 重心 外心B. 重心 内心C. 外心 重心D. 外心 内心5. 设P 是△ABC 所在平面内的一点，BC +BA =2BP ,则( )A. P 、A 、B 三点共线B. P 、A 、C 三点共线C. P 、B 、C 三点共线D. 以上均不正确6. (2011·东莞模拟)如图，在平行四边形ABCD 中，E 为DC 边的中心，且AB = a ,AD =b 则BE =( ) A. b -12a B. b +12a C. a +12b D. a-12b7. 设x 为未知向量，a 、b 为已知向量，解方程2x -(5a +3x -4b )+12a -3b =0 得x =___________a +b8. 设1e ,2e 是不共线的向量,已知向量AB =21e +k 2e ,CB =1e +32e ,CD =21e -2e , 若A,B,D 三点共线,则实数k 的值为. ___________-89. 在△ABC 所在的平面上有一点P ，满足PA +PB +PC =AB ,则△PBC 与△ABC 的面积之比是___________. 解：由PA +PB +PC =AB ,得PA +PB +BA +PC =0,得PC =-2AP ,PBC ABC S S =10. (2010·全国改编)△ABC 中，上，CD 平分∠ACB,若 CB =a ,CA =b ,|a|=1,| b |=2,则CD =___________a +1b 11. (创新题)如图所示,点E 、F ABCD 的对角线AC 、BD 的中点,设DA =a , BC =b ,试用a 、b 表示EF .在△ABC 中,EP 是与BC 平行的中位线∴11PE BC a ==.∴112PF AD b ==-. , EF =11EP PF PE PF a b +=-+=-- 1a b =-+（）4、2课后测试1. 若向量a =（1，1），b =（-1,0），c =（6，4），则c =( ) A. 4a -2b B. 4a +2b C. -2 a +4b D. 2 a +4b2. 若平面向量a ，b 满足|a +b |=1, a +b 平行于x 轴，b =(2,-1)，则a =( ) A. (-1,1) B. (-3,1) C. (-1,1)或(-3,1) D. (1,-1)或(-3,1)3. （2011·东莞模拟）已知向量a =(1,1), b =(2,x),若a +b 与4b -2a 平行，则实数x 的值是( )A. -2B. 0C. 1D. 24. 设非零向量a 、b 、c 满足|a |=|b |=|c |，a +b =c ,则〈a ,b 〉=( ) A. 150° B.120° C. 60° D.30°5. (2011·天津模拟)如图所示，向量OA ,OB ,OC 的终点A,B,C 在一条直线上且AC =-3CB ,设OA =p , OB =q , OC =r ,则下列等式成立的是( )A. r =-p +2qB. r =32p -12qC. r =-1p +3qD. r =2p +q 6. 下列各组向量中，能作为基底的组数为( )①a =(-1,2), b =(5,7);②a =(2,-3), b =(4,-6);③a =(2,-3), b =12,-34. A. 0 B. 1 C. 2 D. 37. 在平面直角坐标系xOy 中，四边形ABCD 的边AB ∥DC,AD ∥BC,已知点A(－2，0)， B （6，8），C(8,6),则D 点的坐标为___________.(0,-2)8. 设1e 、2e 是平面内一组基向量，且a ＝1e ＋22e ，b ＝1e ＋2e ，则向量1e ＋2e 可以表示为另一组基向量a 、b 的线性组合，即1e ＋2e ＝___________a ＋___________b .2 -19. （2011·厦门模拟）如图所示的平行四边形ABCD 中，点M 是AB的中点，点N 在BD 上，且BN ＝13BD ，若AB =a ,AD =b , 试用向量a ,b 表示MN 为___________a +13b 10. 已知向量a =(sin θ,cos θ -2sin θ),b =(1,2),若a ∥b ,则2sin 3cos sin 2cos θθθθ-+的值为11. (2011·徐州模拟)已知A,B,C,D 四点的坐标分别为(1,0),(4,3),(2,4),(0,2), 证明：∵AB =(4,3)-(1,0)=(3,3),CD =(0,2)-(2,4)=(-2,-2),∴AB =-32CD . ∴AB ∥CD 且|AB |≠|CD |，即12. △ABC 的三内角A, B,C 所对边的长分别为a,b,c,设向量p =(a+c,b), q =(b-a,c-a),若p∥q ,求角C 的大小. 解：∵p ∥q ,∴(a+c)(c-a)=b(b-a),4、3课后测试 1.（2011·南京模拟）已知向量a =(1,2)，b =(2,-3). 若向量c 满足(c +a )∥b ，c ⊥(a +b )，则c = ( ) A. (79,73) B. (-73,79) C. (73,79 2. （2010·湖南） 若非零向量a ，b 满足|a |=|b |，(2a +b )·b =0,则a 与b 的夹角为( ) A. 30° B. 60° C. 120° D. 150°3. 已知下列命题中： （1）若k ∈R ，且k b =0，则k=0或b =0;（2）若a ·b =0，则a =0或b =0;（3）若不平行的两个非零向量a ,b ，满足|a |=|b |，则(a +b )·(a -b )=0;（4）若a 与b 平行，则a ·b =|a |·|b |.其中真命题的个数是( ) A. 0 B. 1 C. 2 D. 34. 定义运算|a ⊗b |=|a |·|b |·sin θ,其中θ是向量a , b 的夹角，若|x |=2,|y |=5，x ·y =-6,则|x ⊗y |=（ ） A. 8 B. -8 C. 8或-8 D. 6 5. （2010·河北衡水中学仿真试卷）已知向量a =(1,1), b =(2,n)，若|a +b |=a ·b ,则n 为 ( ) A. -3 B. -1 C. 1 D. 36. 已知a =(2,1)与b =(1,2)，要使|a +t b |最小，则实数t 的值为___________57. （2010·浙江）已知平面向量α,β,|α|=1,| β|=2, α⊥(α-2β)，则|2α+β|的值是___________8. 已知i 、j 为互相垂直的单位向量, a =i -2j j ，b =i +λj ，且a 与b 的夹角为锐角，则实数λ的取值范围是___________9. 已知向量a ＝(sin θ ，1)，b ＝(1，cos θ)，-2π＜θ＜2π. （1）若a ⊥b ，则θ=___________; （2）｜a ＋b ｜的最大值为. ___________ :(1) a ⊥b ⇒a ·b =0sin θ(2)| a +b |=|(sin θ+1, cos 2sin (2sin θ=|a +b |有最大值，最大值为10. (2011·大连模拟)已知a ,b ,c 是单位向量，且a ·b =0,求(a -c )·(b -c )的最小值. A=(a -c )·(b -c ),则A=a ·b -c (a +b )+2c .∵a ,b ,c 为单位向量，∴|a |=|b |=|c |=1,又a ·b =0,∴a ⊥b . |a +b |=2.∴A=1-c ·(a +b )=1-|c |·|a +b |cos 〈c , a +b 〉=1-2〈c , a +b 〉.∵〈c , a +b 〉∈ [0,π∴当〈c , a +b 〉=0时，A min =1-2.11.（2010江苏改）在直角坐标系xOy 中，已知点A(－1,－2)、B(2,3)、C(－2,－1).(1)求以线段AB 、AC 为邻边的平行四边形的两条对角线的长；t 满足(AB -t OC 2）由题设知AB =(3,5), AC =(-1,1),则|AB +AC |=(2,6),AB-AC=(4,4).|AB +AC |=2,|AB -AC |=4故所求的两条对角线的长分别为42, 2由题设知：OC =(-2,-1), AB -t OC =(3+2t,5+t).(AB -t OC )·OC ＜t 2-5,+5t+6＞0,-3或t ＞-2.4.4课后测试一、选择题1. 若A （2，-1），B （-1，3），则的坐标是( )A.（1，2）B.（-3，4）C. （3，-4）D. 以上都不对2.与a=（4，5）垂直的向量是( )A.（-5k,4k ）B. (-10，2） D.（5k, -4k ）3. △ABC 中,=a, =b,则等于( )A.a+bB. -(a+b)C.a -bD.b -a4.化简52(a －b)－31(2a+4b)+152(2a+13b)的结果是( ) A.51a ±51b B.0 C. 51a+51b D. 51a －51b 5.已知|p|=22,|q|=3, p 与q 的夹角为4π,则以a=5p+2q,b=p －3q 为邻边的平行四边形的一条对角线长为( ) A.15 B.15 C. 16 D.14 6.已知A(2,-2),B(4,3),向量p 的坐标为(2k -∥,则k 的值为( )A.109-B.109C.1019- 7. 已知△ABC 的三个顶点，A 、B 、C 及平面内一点P 满足PA PB PC AB ++=，则点P 与△ABC 的关系是 ( )A. P 在△ABC 的内部B. P 在△ABC 的外部C. P 是AB 边上的一个三等分点D. P 是AC 边上的一个三等分点8.已知△ABC 的三个顶点，A (1,5)，B(-2,4)，C(-6,-4)，M 是BC 边上一点,且△ABM 的面积是△ABC面积的41,则线段AM 的长度是( ) A.5 C.25 9.设e 1,e 2是夹角为450的两个单位向量,且a=e 1则|a+b|的值 ( )A.23B.9C.2918+10.若⊥a,则a 与b 的夹角为( )A.300 C.600 D.75011.把一个函数的图象按向量a=(3π,-2)平移后，得到的图象对应的函数解析式为y=sin(x+6π)-2,则原函数的解析式为( ) A.y=sinx B.y=cosx C.y=sinx+2 D.y= -cosx12.在△ABC 中，AB =c, BC = a, CA =b,则下列推导中错误的是 ( )A.若a·b<0,则△ABC 为钝角三角形B. 若a·b=0,则△ABC 为直角三角形C. 若a·b=b·c,则△ABC 为等腰三角形D. 若c·( a+b+c)=0,则△ABC 为等腰三角形二、填空题13.在△ABC ,4==且,8=⋅AC AB 14.一艘船从A 点出发以h km /32h km /2，15. 若向量)4,7(),1,2(),2,3(-=-=-=c b a 16.给出下列命题:①若a 2+b 2=0,则②已知A ),,(11y x B ),(22y x ,则);2,2(212121y y x x ++= ③已知a,b,c 是三个非零向量,若a+b=0,则|a·c|=|b·c| ④已知0,021>>λλ,e 1,e 2是一组基底,a=λ1e 1+λ2e 2则a 与e 不共线,a 与e 2也不共线;⑤若a 与b 共线,则a·b=|a|·|b|.三、解答题17.如图,ABCD 是一个梯形,//=, M 、N 分别是,的中点,已知=a,=b,M D C试用a、b表示,DC BC和.MN18.设两个非零向量e1、e2不共线.如果=e1+e2,=2e1+8e2,=3(e1-e2)⑴求证:A、B、D共线;⑵试确定实数k,使ke1+e2和e1+ke2共线.解：⑴∵BD BC CD=+=5e1+5e2=AB5, ∴BDAB//又有公共点B,∴A、B、D共线⑵设存在实数λ使ke1+e2=λ(e1+ke2) ∴k=λ且kλ=1 ∴k=1±19.已知△ABC中,A(2,4),B(-1,-2),C(4,3),BC边上的高为AD.⑴求证:AB⊥AC;⑵求点D与向量的20.已知△ABC的三个顶点为A(1,2),B(4,1),C(3,4).⑴求AB边上的中线CM的长;⑵在AB上取一点求P点的坐标.）2 APQBPQCSAP AB S∆=∴=,3(32)2-=。

北京理工大学附中2013届高考数学二轮复习精品训练：计数原理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．“2012”含有数字0, 1, 2，且有两个数字2，则含有数字0, 1, 2，且有两个相同数字的四位数的个数为( )A ．18B ．24C ．27D ．36【答案】B2．将5名同学分到甲、乙、丙3个小组，若甲组至少两人，乙、丙组至少各一人，则不同的分配方案的种数为( )A ．80B ．120C ．140D ． 50【答案】A3．若},6,5,4,3,2,1{)2,1,0(},1010|{,0122∈=+⨯+⨯=∈i a a a a x x n m i 其中并且606=+n m ，则实数对（m ，n ）表示平面上不同点的个数为( )A ．32个B ．30个C ．62个D ．60个【答案】D4．从5位男实习教师和4位女实习教师中选出3位教师派到3个班实习班主任工作，每班派一名，要求这3位实习教师中男女都要有，则不同的选派方案共有( )A ．210B ．420C ．630D ．840【答案】B5．若2012220120122012(12)x a a x a x a x -=++++,则01122320112012()()()()a a a a a a a a ++++++++=( ) A ．1B ．20122C ．201212-D ．201222-【答案】C 6．()612-x 展开式中2x 的系数为( ) A ．15 B ．60 C ．120 D ．240【答案】B7．体育老师把9个相同的足球放入编号为1,2,3的三个箱中，要求每个箱子放球的个数不少于其编号，则不同的方法有( )A ．28种B ．16种C ．10种D ． 42种【答案】C8．已知复数a bi +，其中,a b 为0，1，2，…，9这10个数字中的两个不同的数，则不同的虚数的个数为( )A ．36B ．72C ．81D ．90【答案】C 9．设函数2221210()(20)(20)(20)f x x x c x x c x x c =-+-+-+，集合M ={|()0}x f x ==1219{,,,}x x x ⊆*N ，设1210c c c ≥≥≥，则110c c -=( )A ．83B ．85C ．79D ． 81 【答案】D10．n ∈N *，则（20-n ）(21-n)……(100-n)等于( )A ．80100n A -B ．n n A --20100C ．81100n A -D ．8120n A - 【答案】C11．一个旅游景区的游览线路如图所示，某人从点P 处进，Q 点处出，沿图中线路游览A 、B 、C 三个景点及沿途风景，则不童复（除交汇点O 外）的不同游览线路有( )种A ．6B ． 8C ． 12D ． 48 【答案】D12．记123n a a a a 为一个n 位正整数，其中12,,,n a a a 都是正整数，119,09(2,3,,)i a a i n ≤≤≤≤=．若对任意的正整数(1)j j n ≤≤，至少存在另一个正整数(1)k k n ≤≤，使得j k a a =，则称这个数为“n 位重复数”．根据上述定义，“四位重复数”的个数为( ) A ．1994个B ．4464个C ．4536个D ．9000个 【答案】B第Ⅱ卷(非选择题 共90分) 二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．已知30sin a xdx π=⎰，则71x x ax ⎛⎫+ ⎪⎝⎭的展开式中的常数项是 (用数字作答）. 【答案】56014．n x )1(+的展开式中，某一项的系数为7，则展开式中第三项的系数是________．【答案】21 15．6()y y x的展开式中3x 的系数等于 【答案】1516．设3(n x x-的展开式的各项系数之和为M ，二项式系数之和为N ，若M+N=16，则展开式中的常数项为 .【答案】4-三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17． 一个盒子装有七张卡片，上面分别写着七个定义域为R 的函数：31)(x x f =，22)(x x f =，x x f =)(3，x x f cos )(4=，x x f sin )(5=，x x f -=2)(6,2)(7+=x x f 。

北京理工大学附中2013届高考数学二轮复习精品训练：平面向量本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．函数tan()42y x ππ=-的部分图像如图1所示，则()OA OB AB +⋅=( )A ．4B ．6C ．1D ．2【答案】B2．已知|p|=22,|q|=3,p 、q 的夹角为4π，如图，若=5p+2q,=p-3q,D 为BC 的中点，则||为()A ．215B ．215C ．7D ．18【答案】A3．若,,a b c 均为单位向量，且0,()()0a b a c b c =--≤，则||a b c +-的最小值为( )A ． 2B ．C ． 1D ． 21【答案】D4．已知平面向量，且∥，则实数的值等于( )A ．或B ．C ．或D ．【答案】C5．设向量,满足:1||=a , 2||=b , 0(=+⋅b)a a , 则与的夹角是A ． 30B ． 60C ． 90D ． 120【答案】D6．已知平面向量，，若，，，则的值为( )A ．B ．C ．D ．【答案】B7．在边长为1的等边ABC ∆中，设,,BC a CA b AB c a b b c c a ===⋅+⋅+⋅=，则( )A ．32- B ．0 C ．32 D ．3【答案】A8．在同一平面内，已知)sin ,(cos ),sin ,(cos ββαα==，且0=⋅，若)sin 2,(cos ),sin 2,(cos ββαα='='B O O ，则B O A ''∆的面积等于( )A ．2B ．1C ．21D ．41【答案】B9．向量(1,2)a =-，(6,3)b =.则a 与b 的夹角是( )A ． 60oB ． 90oC ． 120oD ． 150o【答案】B10．平面向量(,3),(2,1),(1,)a x b c y =-=-=，若(),//()a b c b a c ⊥-+则b 与c 的夹角为( )A ．0B ．4πC ．2πD ．34π【答案】C11．已知向量a b ⊥，向量c 与,a b 的夹角都是60，且||1,||2,||3a b c ===，则2)(c b a ++=( )A ． 6B ． 5C ． 23D ． 8【答案】C12．⊿ABC 中，0)()(=+⋅+BO OC AC AB ,6=⋅,则⊿ABC 的形状为( )A ．直角等腰三角形B ．锐角等腰三角形C ．钝角等腰三角形D ．不等边三角形【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．设a ，b ，c 是单位向量，且a b c =+，则向量a ，b 的夹角等于．【答案】o 6014．设(,3)a x =，(2,1)b =-，若a 、b 夹角为钝角，则x 的取值范围是____________；【答案】3(,6)(6,)2-∞-- 15．已知点)2,1(),1,0(),1,2(),0,1(--D C B A ，则与的夹角大小为____________【答案】π16．已知||2a =，||3b =，,a b 的夹角为60°，则|2|ab -=．【答案】三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．)cos 1,(sin A A a -=→已知)0,2(=→b 且向量→→b a 与所成的角为3π,其中的内角为ABC C B A ∆,, (1)求角A 的值,(2)求C B sin sin +的取值范围【答案】 (1) ∵→→b a 与所成的角为3π,∴ 代入化简得到:01cos 2cos 2=--A A解得:1cos =A (舍去)或21cos -=A ∴32π=A (2) ∵32π=A ∴B C C B -==+3,3ππ即 令)3sin()3sin(sin sin sin ππ+=-+=+=B B B C B y ∵)3,0(π∈B ,∴)32,3(3πππ∈+B ∴123≤<y 18．若直线02:=++y mx l 与线段AB 有交点，其中A （-2，3），B(3,2),求m 的取值范围.【答案】设l 交有向线段AB 于点P （x,y ）且点）时直线过，当A PBAP 00(=≥=λλλ 则可得3425,0435*******-<≥≥+-=⎪⎩⎪⎨⎧++=++-=m m m m l P y x 或得上，故可得点在因λλλλλ 由于设λ时，无形中排除了P,B 重合的情形，要将B 点坐标代入直线方程得3425,34-≤≥-=m m m 或故 19．已知ABC △的面积为1，且满足2≥⋅，设AB 和AC 的夹角为θ．(1）求θ的取值范围；(2）求函数⎪⎭⎫ ⎝⎛+-=4cos 22cos 3)(2πθθθf 的最小值． 【答案】（1）设ABC △中角A B C ，，的对边分别为a b c ，，， 则由1sin 21=θbc ，2cos ≥θbc ， 可得1cot ≥θ，⎥⎦⎤ ⎝⎛∈∴4,0πθ． (2）132sin 24cos 22cos 3)(2-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++=πθπθθθf ⎥⎦⎤ ⎝⎛∈4,0πθ ，⎥⎦⎤ ⎝⎛∈+∴65,332πππθ， 所以，当6532ππθ=+，即4πθ=时，.0)(min =θf20．已知向量=,=，且x ∈。