2020版高考数学理科(人教B版)一轮复习课时规范练55 分类加法计数原理与分步乘法计数原理+Word版含解析

课时规范练(A)课时规范练1集合的概念与运算课时规范练3命题及其关系、充要条件课时规范练5函数及其表示课时规范练7函数的奇偶性与周期性课时规范练9指数与指数函数课时规范练11函数的图象课时规范练13函数模型及其应用课时规范练15利用导数研究函数的单调性课时规范练17定积分与微积分基本定理课时规范练19同角三角函数基本关系式及诱导公式课时规范练21简单的三角恒等变换课时规范练23函数y=A sin(ωx+φ)的图象及三角函数的应用课时规范练25平面向量的概念及线性运算课时规范练27平面向量的数量积及其应用课时规范练29数列的概念课时规范练31等比数列课时规范练33二元一次不等式(组)与简单的线性规划问题课时规范练35合情推理与演绎推理课时规范练37数学归纳法课时规范练39空间几何体的表面积与体积课时规范练41空间直线、平面的平行关系课时规范练43空间向量及其运算课时规范练45直线的倾斜角、斜率与直线的方程课时规范练47圆的方程课时规范练49椭圆课时规范练51抛物线课时规范练53算法初步课时规范练55用样本估计总体课时规范练57分类加法计数原理与分步乘法计数原理课时规范练59二项式定理课时规范练61古典概型与几何概型课时规范练63二项分布与正态分布课时规范练65极坐标方程与参数方程课时规范练67绝对值不等式课时规范练(B)课时规范练2简单不等式的解法课时规范练4简单的逻辑联结词、全称量词与存在量词课时规范练6函数的单调性与最大(小)值课时规范练8幂函数与二次函数课时规范练10对数与对数函数课时规范练12函数与方程课时规范练14导数的概念及运算课时规范练16利用导数研究函数的极值、最大(小)值课时规范练18任意角、弧度制及任意角的三角函数课时规范练20两角和与差的正弦、余弦与正切公式及二倍角公式课时规范练22三角函数的图象与性质课时规范练24余弦定理、正弦定理及应用举例课时规范练26平面向量基本定理及向量坐标运算课时规范练28复数课时规范练30等差数列课时规范练32数列求和课时规范练34基本不等式及其应用课时规范练36直接证明与间接证明课时规范练38空间几何体的结构及其三视图、直观图课时规范练40空间点、直线、平面之间的位置关系课时规范练42空间直线、平面的垂直关系课时规范练44空间几何中的向量方法课时规范练46点与直线、两条直线的位置关系课时规范练48直线与圆、圆与圆的位置关系课时规范练50双曲线课时规范练52直线与圆锥曲线的位置关系课时规范练54随机抽样课时规范练56变量间的相关关系、统计案例课时规范练58排列与组合课时规范练60随机事件的概率课时规范练62离散型随机变量及其分布列课时规范练64离散型随机变量的均值与方差课时规范练66极坐标方程与参数方程的应用课时规范练68不等式的证明解答题专项解答题专项一函数与导数的综合问题第1课时利用导数证明不等式第2课时利用导数研究不等式恒(能)成立问题第3课时利用导数研究函数的零点解答题专项二三角函数与解三角形解答题专项三数列解答题专项四立体几何中的综合问题解答题专项五直线与圆锥曲线第1课时圆锥曲线中的最值(或范围)问题第2课时圆锥曲线中的定点(或定值)问题第3课时圆锥曲线中的存在性(或证明)问题解答题专项六概率与统计单元质检卷单元质检卷一集合与常用逻辑用语单元质检卷二函数单元质检卷三导数及其应用单元质检卷四三角函数、解三角形单元质检卷五平面向量、数系的扩充与复数的引入单元质检卷六数列单元质检卷七不等式、推理与证明单元质检卷八立体几何单元质检卷九解析几何单元质检卷十算法初步、统计与统计案例单元质检卷十一计数原理单元质检卷十二概率。

课时规范练57 分类加法计数原理与分步乘法计数原理基础巩固组1.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )A.40B.16C.13D.10答案:C解析:分两类情况讨论:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面.根据分类加法计数原理知,共可以确定8+5=13(个)不同的平面.2.(河南洛阳模拟)一个电路中含有(1)(2)两个零件,零件(1)含有A,B两个元件,零件(2)含有C,D,E三个元件,每个零件中有一个元件能正常工作则该零件就能正常工作,则该电路能正常工作的线路条数为( )A.9B.8C.6D.5答案:C解析:由分步乘法计数原理易得,该电路能正常工作的线路条数为2×3=6(条).故选C.3.有5名学生志愿者到2个小区参加疫情防控常态化宣传活动,每名学生只去1个小区,每个小区至少安排1名学生,则不同的安排方法有( ) A.10种 B.20种 C.30种 D.40种答案:C解析:根据题意,将5名学生志愿者安排到2个小区,每个人都有2种安排方法,则5个人有2×2×2×2×2=32(种)不同的安排方法,其中5人都去1个小区的安排方法有2种,则符合题意的安排方法有32-2=30(种).4.(安徽马鞍山一模)现有4名志愿者要安排到3个服务站点参加服务,每名志愿者只能安排到一个站点,每个站点至少安排一名志愿者,则不同的安排方案共有( )A.48种B.36种C.24种D.12种答案:B解析:先将4名志愿者分成3组,其中2组1人,1组2人,有C42种分法,再将3组人分给3个服务站有C42·A33=36(种)安排方案.故选B.5.(山西临汾三模)五一劳动节期间,有6名志愿者要去3所敬老院做义工,这3所敬老院的规模不同,其中2所敬老院规模较小,各需1名义工,剩余4人均去另1所,则不同的分配方案有种.答案:30解析:第一步:先从6名志愿者中选取4名志愿者去一所养老院,有C64种方法;第二步:将剩下的2名志愿者分别安排在剩下的2所养老院中,有A22种方法.根据分步乘法计数原理,有C64A22=30(种)方法.6.任取集合{1,2,3,4,…,10}中三个不同数a1,a2,a3,且满足a2-a1≥2,a3-a2≥3,则选取这样的三个数的方法共有种.答案:35解析:第一类,a3-a1=5,a1,a3的值有5种情况,则a2只有1种情况,共有5×1=5(种)情况;第二类,a3-a1=6,a1,a3的值有4种情况,则a2有2种情况,共有4×2=8(种)情况;第三类,a3-a1=7,a1,a3的值有3种情况,则a2有3种情况,共有3×3=9(种)情况;第四类,a3-a1=8,a1,a3的值有2种情况,则a2有4种情况,共有2×4=8(种)情况;第五类,a3-a1=9,a1,a3的值有1种情况.则a2有5种情况,共有1×5=5(种)情况.则选取这样的三个数的方法共有5+8+9+8+5=35(种).7.如图所示线路图,机器人从A 地经B 地走到C 地,最近的走法共有 种.答案:20解析:A 到B 共2种最近的走法,从B 到C 共C 52种最近的走法,由分步乘法计数原理,知从A 地经B 地走到C 地,最近的走法共有2C 52=20(种).综合提升组8.(河南郑州一模)为了落实五育并举,全面发展学生素质,学校准备组建书法、音乐、美术、体育社团,现将5名同学分配到这4个社团进行培训,每名同学只分配到1个社团,每个社团至少分配1名同学,则不同的分配方案共有( ) A.60种 B.120种 C.240种 D.480种答案:C解析:由题意,分步完成,第一步,将5名同学按1,1,1,2分成4组,有C 51C 41C 31C 22A 33种分组方法;第二步,将分成4组的学生安置在4个社团,有A 44种方法,由分步乘法计数原理得,共有C 51C 41C 31C 22A 33·A 44=240(种)不同的分配方案,故选C.9.如图,在由若干个同样小的平行四边形组成的大平行四边形内有一个★,则含有★的平行四边形共有个.(用数字作答)答案:48解析:含有★的平行四边形的左上角的顶点有4种可能,右下角的顶点有12种可能.由一个左上角顶点和一个右下角顶点就能构成一个平行四边形,所以共有48个含有★的平行四边形.10.如图,矩形的对角线把矩形分成A,B,C,D四部分,现用5种不同颜色给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,则共有种不同的涂色方法.答案:260解析:由题意,区域A有5种涂色方法;区域B有4种涂色方法;区域C的涂色方法可分2类:若C与A涂同色,区域D有4种涂色方法;若C与A涂不同色,此时区域C有3种涂色方法,区域D也有3种涂色方法.所以共有5×4×4+5×4×3×3=260(种)涂色方法.创新应用组11.某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自同一个家庭的乘坐方式共有( )A.18种B.24种C.36种D.48种答案:B解析:根据题意,分2类情况讨论:①A户家庭的孪生姐妹在甲车上,甲车上剩下两个要来自不同的家庭,可以在剩下的三个家庭中任选2个家庭,再从每个家庭的2个小孩中任选一个,来乘坐甲车,有3×2×2=12(种)乘坐方式;②A户家庭的孪生姐妹不在甲车上,需要在剩下的三个家庭中任选1个家庭,让其2个小孩都在甲车上,对于剩余的2个家庭,从每个家庭的2个小孩中任选一个,来乘坐甲车,有3×2×2=12(种)乘坐方式.则共有12+12=24(种)乘坐方式,故选B.。

【30份】2020版高考数学北师大版（理）一轮复习课时规范练目录课时规范练1集合的概念与运算 (2)课时规范练2不等关系及简单不等式的解法 (5)课时规范练3命题及其关系、充要条件 (11)课时规范练4简单的逻辑联结词、全称量词与存在量词 (15)课时规范练5函数及其表示 (20)课时规范练6函数的单调性与最值 (24)课时规范练7函数的奇偶性与周期性 (30)课时规范练8幂函数与二次函数 (35)课时规范练9指数与指数函数 (40)课时规范练10对数与对数函数 (45)课时规范练11函数的图像 (50)课时规范练12函数与方程 (55)课时规范练13函数模型及其应用 (61)课时规范练14导数的概念及运算 (68)课时规范练15导数与函数的小综合 (72)课时规范练16定积分与微积分基本定理 (78)课时规范练17任意角、弧度制及任意角的三角函数 (82)课时规范练18同角三角函数的基本关系及诱导公式 (88)课时规范练19三角函数的图像与性质 (94)课时规范练20函数y=A sin(ωx+φ)的图像及应用 (102)课时规范练21两角和与差的正弦、余弦与正切公式 (112)课时规范练22三角恒等变换 (121)课时规范练23解三角形 (129)课时规范练24平面向量的概念及线性运算 (137)课时规范练25平面向量基本定理及向量的坐标表示 (143)课时规范练26平面向量的数量积与平面向量的应用 (149)课时规范练27数系的扩充与复数的引入 (154)课时规范练28数列的概念与表示 (158)课时规范练29等差数列及其前n项和 (163)课时规范练30等比数列及其前n项和 (169)2019年5月课时规范练1集合的概念与运算基础巩固组1.(2018厦门外国语学校一模,2)已知集合A={x|y=lg(x-1)},B={x||x|<2},则A∩B=()A.(-2,0)B.(0,2)C.(1,2)D.(-2,2)2.已知全集U=R,集合A={x|x<-2或x>2},则?U A=()A.(-2,2)B.(-∞,-2)∪(2,+∞)C.[-2,2]D.(-∞,-2]∪[2,+∞)3.(2018百校联盟四月联考,1)设集合A={-1,0,1,2},B={y|y=2x,x∈A},则A∪B中元素的个数为()A.5B.6C.7D.84.设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则S∩T=()A.[2,3]B.(-∞,2]∪[3,+∞)C.[3,+∞)D.(0,2]∪[3,+∞)5.(2018北京101中学3月模拟,1)已知集合A={x|x(x-2)<0},B={x|ln x>0},则A∩B是()A.{x|x>0}B.{x|x>2}C.{x|1<x<2}D.{x|0<x<2}6.设集合M={-4,-3,-2,-1,0,1},N={x∈R|x2+3x<0},则M∩N=()A.{-3,-2,-1,0}B.{-2,-1,0}C.{-3,-2,-1}D.{-2,-1}7.(2018山东济南二模,1)设全集U=R,集合A={x|x-1≤0},集合B={x|x2-x-6<0},则下图中阴影部分表示的集合为()A.{x|x<3}B.{x|-3<x≤1}C.{x|x<2}D.{x|-2<x≤1}8.已知全集U=R,A={0,1,2,3},B={y|y=2x,x∈A},则(?U A)∩B=()A.(-∞,0)∪(3,+∞)B.{x|x>3,x∈N}C.{4,8}D.[4,8]9.(2018湖南衡阳一模,1)已知集合A={x|(x+1)(x-3)<0},B={x|y=ln x},则A∩B=()A.{0,3}B.(0,3)C.(-1,3)D.{-1,3}10.已知集合A={x|x(x-4)<0},B={0,1,5},则A∩B=.11.已知集合A={x|log2x≤2},B={x|x<a},若A?B,则实数a的取值范围是.12.设A,B是全集I={1,2,3,4}的子集,A={1,2},则满足A?B的B的个数为.综合提升组13.已知集合A={x|x2-2x-3≤0},B={x|x<a},若A?B,则实数a的取值范围是()A.(-1,+∞)B.[-1,+∞)C.(3,+∞)D.[3,+∞)14.(2018河北衡水中学十模,1)已知全集U=Z,A={0,1,2,3},B={x|x2=2x},则A∩(?U B)=()A.{1,3}B.{0,2}C.{0,1,3}D.{2}15.已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是()A.(-2,1)B.[-1,0]∪[1,2)C.(-2,-1)∪[0,1]D.[0,1]16.已知集合A={x|4≤2x≤16},B=[a,b],若A?B,则实数a-b的取值范围是.创新应用组17.已知集合A={x|x<a},B={x|1<x<2},且A∪(?R B)=R,则实数a的取值范围是()A.a≤1B.a<1C.a≥2D.a>218.若集合A={x|x2+4x+k=0,x∈R}中只有一个元素,则实数k的值为.参考答案课时规范练1集合的概念与运算1.C由题意,可知A={x|x>1},B={x|-2<x<2},∴A∩B={x|1<x<2},表示为区间即(1,2),故选C.2.C因为A={x|x<-2或x>2},所以?U A={x|-2≤x≤2}.故选C.3.B因为A={-1,0,1,2},B=,所以A∪B=-1,0,,1,2,4,A∪B中元素的个数为 6.4.D由(x-2)(x-3)≥0,解得x≥３或x≤2,所以S={x|x≤２或x≥3}.因为T={x|x>0},所以S∩T={x|0<x≤２或x≥3},故选D.5.C由题意,集合A={x|x(x-2)<0}={x|0<x<2},B={x|ln x>0}={x|x>1},所以A∩B={x|1<x<2}.故选C.6.D集合M={-4,-3,-2,-1,0,1},N={x∈R|x2+3x<0}={x|-3<x<0},∴M∩N={-2,-1}.故选D.7.D由题意可得:A={x|x≤1},B={x|-2<x<3},∴A∩B={x|-2<x≤1},故选 D.8.C∵全集U=R,A={0,1,2,3},B={y|y=2x,x∈A}={1,2,4,8},∴(?U A)∩B={4,8}.故选 C.9.B A={x|-1<x<3},B={x|x>0},所以A∩B=(0,3),故选 B.10.{1}A={x|x(x-4)<0}=(0,4),所以A∩B={1}.11.(4,+∞)由log2x≤2,得0<x≤4,即A={x|0<x≤4},而B={x|x<a},由于A?B,则a>4.12.4因为A={1,2}且A?B,所以B={1,2}或B={1,2,3}或B={1,2,4}或B={1,2,3,4}.13.C由题意,A=[-1,3],B=(-∞,a),∵A?B,∴a>3,∴a的取值范围是(3,+∞).14.A∵全集U=Z,A={0,1,2,3},B={x|x2=2x},∴?U B={x|x∈Z,且x≠0,且x≠2},∴A∩（?U B)={1,3}.故选 A.A∪B).15.C由题意可知阴影部分对应的集合为(?U(A∩B))∩（∵A={x|-2<x<0},B={x|-1≤x≤1},∴A∩B={x|-1≤x<0},A∪B={x|-2<x≤1},∵?U(A∩B)={x|x<-1或x≥0},∴(?U(A∩B))∩（A∪B)={x|0≤x≤１或-2<x<-1}.故选 C.16.(-∞,-2]集合A={x|4≤２x≤16}={x|22≤２x≤２4}={x|2≤x≤4}=[2,4].因为A?B,所以a≤2,b≥４.所以a-b≤２-4=-2.故实数a-b的取值范围是(-∞,-2].17.C∵A∪(?R B)=R,∴B?A,∴a≥2,故选C.18.4由题意x2+4x+k=0有两个相等的实根,∴Δ＝16-4k=0,解得k=4.2019年5月课时规范练2不等关系及简单不等式的解法基础巩固组1.已知a,b∈R,下列命题正确的是()A.若a>b,则|a|>|b|B.若a>b,则C.若|a|>b,则a2>b2D.若a>|b|,则a2>b22.函数f(x)=的定义域是()A.(-∞,1)∪(3,+∞)B.(1,3)C.(-∞,2)∪(2,+∞)D.(1,2)∪(2,3)3.已知实数a,b,c满足b+c=6-4a+3a2,c-b=4-4a+a2,则a,b,c的大小关系为()A.a<b≤cB.b≤c<aC.b<c<aD.b<a<c4.使不等式2x2-5x-3≥0成立的一个充分不必要条件是()A.x≥0B.x<0或x>2C.x∈{-1,3,5}D.x≤-或x≥35.若函数f(x)=的定义域为R,则实数m的取值范围为()A.[-4,0]B.[-4,0)C.(-4,0)D.(-∞,4]∪{0}。

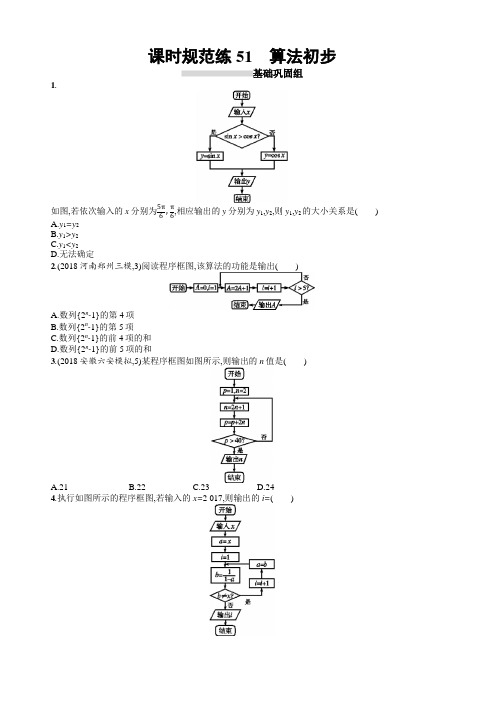
课时规范练51算法初步基础巩固组1.如图,若依次输入的x分别为,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定2.(2018河南郑州三模,3)阅读程序框图,该算法的功能是输出()A.数列{2n-1}的第4项B.数列{2n-1}的第5项C.数列{2n-1}的前4项的和D.数列{2n-1}的前5项的和3.(2018安徽六安模拟,5)某程序框图如图所示,则输出的n值是()A.21B.22C.23D.244.执行如图所示的程序框图,若输入的x=2 017,则输出的i=()A.2B.3C.4D.55.执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为()A.0B.1C.2D.36.(2018山东、湖北重点中学冲刺模拟,5)按如图所示的程序框图,某同学在区间[0,92]上随机地取一个数作为x输入,则该同学能得到“OK”的概率为()A. B.C. D.7.(2018湖南长郡中学开学考试,6)执行如图所示的程序框图,输出的结果是()A.8B.6C.5D.38.(2018湖南岳阳一模,9)我国古代伟大的数学家秦九韶提出了一种将一元n次多项式的求值问题转化为n个一次式的算法,数学上称之为秦九韶算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为()A.15B.31C.69D.127END10.(2018江西南昌模拟,5)执行如图所示的程序框图,输出S的值为()A.15B.16C.24D.2511.(2018福建莆田三模,8)相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.“三分损益”包含“三分损一”和“三分益一”,用现代数学的方法解释如下,“三分损一”是在原来的长度减去一分,即变为原来的三分之二;“三分益一”是在原来的长度增加一分,即变为原来的三分之四,如图的程序是与“三分损益”结合的计算过程,若输入的x的值为1,输出的x的值为()A. B. C. D.12.(2018山东日照4月联考,12)条形码是由一组规则排列的条、空及其对应的代码组成,用来表示一定的信息,我们通常见的条形码是“EAN-13”通用代码,它是由从左到右排列的13个数字(用a1,a2,…,a13表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中a13是校验码,用来校验前12个数字代码的正确性.图(1)是计算第13位校验码的程序框图,框图中符号[M]表示不超过M的最大整数(例如[365.7]=365).现有一条形码如图(2)所示(97a37040119917),其中第3个数被污损,那么这个被污损的数字a 3是()图(1)图(2)A.6B.7C.8D.913.某地区出租车收费办法如下:不超过2公里收7元;超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元(其他因素不考虑),计算收费标准的程序框图如图所示,则①处应填()A.y=2.0x+2.2B.y=0.6x+2.8C.y=2.6x+2.0D.y=2.6x+2.814.(2018福建宁德5月质检,15)我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人,他在《张丘建算经》中给出一个解不定方程的百鸡问题,问题如下:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?用代数方法表述为:设鸡翁、鸡母、鸡雏的数量分别为x,y,z,则鸡翁、鸡母、鸡雏的数量即为方程组的解.其解题过程可用框图表示如下图所示,则框图中正整数m的值为.15.阅读如图所示的程序框图,运行相应的程序,则输出S的值为.16.(2018中原名校预测金卷,14)如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b,i的值分别为8,6,1,输出a和i的值,若正数x,y满足=1,则ax+iy的最小值为.课时规范练51算法初步1.C由程序框图可知,当输入的x为时,sin>cos成立,所以输出的y1=sin;当输入的x为时,sin>cos不成立,所以输出的y2=cos,所以y1<y2.2.B模拟程序的运行,可得:A=0,i=1,执行循环体,A=2×0+1=1=21-1,i=2;不满足条件i>5,执行循环体,A=2×1+1=3=22-1,i=3;不满足条件i>5,执行循环体,A=2×3+1=7=23-1,i=4;不满足条件i>5,执行循环体,A=2×7+1=15=24-1,i=5;不满足条件i>5,执行循环体,A=2×15+1=31=25-1,i=6;满足条件i>5,退出循环,输出A的值为31.观察规律可得该算法的功能是输出数列{2n-1}的第5项.故选B.3.C执行程序框图,有p=1,n=2,第1次执行循环体,有n=5,p=11;不满足条件p>40,第2次执行循环体,有n=11,p=33;不满足条件p>40,第3次执行循环体,有n=23,p=79;满足条件p>40,输出n的值为23.故选C.4.B根据题意,得a=2 017,i=1,b=-,i=2,a=-,b=,i=3,a=,b=2 017,不满足b≠x,退出循环,输出i=3.故选B.5.C先画出x,y满足的约束条件对应的可行域如图中的阴影部分.平移直线l0:y=-2x.当直线经过点A(1,0)时,y=-2x+S中截距S最大,此时S max=2×1+0=2.与x≥0,y≥0,x+y≤1不成立时S=1进行比较,可得S max=2.6.C当x∈0,,由算法可知y=-2x+2得y∈[1,2],得到“OK”;当x∈,1,由算法可知y=-2x+2得y∈(0,1),不能得到“OK”;当x∈[1,3),由算法可知y=log3x得y∈[0,1),不能得到“OK”;当x∈[3,9],由算法可知y=log3x得y∈[1,2],能得到“OK”;∴P=,故选C.7.A根据程序框图算法原理,计算过程如下:x=1,y=1,z=x+y=2,执行“是”,x=1,y=2,z=3,执行“是”,x=2,y=3,z=5,执行“是”,x=3,y=5,z=8,执行“否”.输出z=8.故选A.8.B由题意,初始值n=4,x=2,执行程序框图:第一次循环:满足条件,v=1×2+1=3,i=2;第二次循环:满足条件,v=3×2+1=7,i=1;第三次循环:满足条件,v=7×2+1=15,i=0;第一次循环:满足条件,v=15×2+1=31,i=-1,此时终止循环,输出结果S=31,故选B.9.3∵a=2,b=3,∴a<b,应把b的值赋给m,∴m的值为3.10.B执行循环程序,当i=1时,1<5,i为奇数,S=1;当i=2时,2<5,i为偶数,S=1+2=3;当i=3时,3<5,i为奇数,S=3+5=8;当i=4时,4<5,i为偶数,S=8+8=16;当i=5时,5≥5,结束循环,输出S=16.故选B.11.B因为x=1⇒x=,i=2⇒x=,i=3⇒x=,i=4,结束循环,输出结果x=,故选B.12.B由程序框图可知,S表示的结果为前12项中所有偶数项之和,T表示的结果为前12项中所有奇数项之和,则:S=7+7+4+1+9+1=29,T=9+a3+0+0+1+9=19+a3,M=3×29+19+a3=106+a3,由检验码,a13=7,可知N=10-a13=3,结合选项进行检验:若a3=6,则N=106+a3-×10=106+6-×10=2,不合题意;若a3=7,则N=106+a3-×10=106+7-×10=3,符合题意;若a3=8,则N=106+a3-×10=106+8-×10=4,不合题意;若a3=9,则N=106+a3-×10=106+9-×10=5,不合题意.故选B.13.D当满足条件x>2时,即里程超过2公里.里程超过2公里时,每车收燃油附加费1元,并且超过的里程每公里收2.6元,即y=2.6(x-2)+7+1=8+2.6(x-2),整理可得y=2.6x+2.8.故选D.14.4由得y=25-x,故x必为4的倍数,当x=4t时,y=25-7t,由y=25-7t>0得t的最大值为3,故判断框应填入的是“t<4?”,故m=4.15.4第一次循环:S=8,n=2;第二次循环:S=2,n=3;第三次循环:S=4,n=4;满足条件n>3,结束循环,输出S=4.16.49输入a,b,i的值分别为8,6,1,第一次循环,i=2,a=2;第二次循环,i=3,b=4;第三次循环,i=4,b=2;第四次循环,i=5,b=a;退出循环,输出a=2,i=5,ax+iy=(2x+5y)=4+25+49,当x=y时,等号成立,即ax+iy的最小值为49,故答案为49.。

课时规范练55分类加法计数原理与分步乘法计数原理基础巩固组1.(2019河北阜平一中模拟,5)将6名留学归国人员分配到济南、青岛两地工作,若济南至少安排2人,青岛至少安排3人,则不同的安排方法数是()A.120B.150C.35D.65名留学归国人员分配到济南、青岛两地工作.若济南至少安排2人,青岛至少安排3人,分两类,第一类,青岛安排3人,济南安排3人,有C63=20种;第二类,青岛安排4人,济南安排2人,有C64=15种.根据分类计数原理可得20+15=35种.故选C.2.(2019安徽蚌埠质检,7)某电商为某次活动设计了“和谐”“爱国”“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同.员工甲按规定依次点击了4次,直到第4次才获奖.则他获得奖次的不同情形种数为()A.9B.12C.18D.24,若员工甲直到第4次才获奖,则其第4次才集全“和谐”“爱国”“敬业”三种红包,则甲第4次获得的红包有3种情况,前三次获得的红包为其余的2种,有23-2=6种情况,则他获得奖次的不同情形种数为3×6=18种.故选C.3.(2019湖南师范大学附中、岳阳一中等六校联考,7)若m,n均为非负整数,在做m+n的加法时各位均不进位(例如:2 019+100=2 119),则称(m,n)为“简单的”有序对,而m+n称为有序对(m,n)的值,那么值为2 019的“简单的”有序对的个数是()A.100B.96C.60D.30,只要确定了m,n即可确定,则可确定一个有序数对(m,n),则对于数m,利用分步计数原理,第一位取法有3种:0,1,2;第二位取法有1种:0;第三位取法有2种:0,1;第四位取法有10种:0,1,2,3,4,5,6,7,8,9;所以值为2 019的“简单的”有序对的个数是3×1×2×10=60.故选C.4.(2019贵州铜仁一中模拟,7)现有4种不同的颜色要对图形中(如图)的四个部分涂色,要求有公共边的两部分不能用同一颜色,则不同的涂色方法有()种A.24B.30C.48D.50,对于区域A,有4种颜色可选,有4种涂色方法;对于区域B,与区域A相邻,有3种颜色可选,有3种涂色方法;对于区域C,与区域AB相邻,有2种颜色可选,有2种涂色方法;对于区域D,与区域AC相邻,有2种颜色可选,有2种涂色方法.则不同的涂色方法有4×3×2×2=48种.故选C.5.某学校开设“蓝天工程博览课程”,组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有()A.A62×A54种B.A62×54种C.C62×54种D.C62×A54种,所以参观甲博物馆的年级有C62种情况,其余年级均有5种选择,所以共有54种情况,根据分步乘法计数原理可得共有C62×54种情况,故选C.6.(2019黑龙江大庆模拟,8)数学与自然、生活相伴相随,无论是蜂的繁殖规律,树的分枝,还是钢琴音阶的排列,当中都蕴含了一个美丽的数学模型Fibonacci(斐波那契数列):1,1,2,3,5,8,13,21…,这个数列前两项都是1,从第三项起,每一项都等于前面两项之和,请你结合斐波那契数列,尝试解答下面的问题:小明走楼梯,该楼梯一共8级台阶,小明每步可以上一级或二级,请问小明的不同走法种数是() A.20 B.34 C.42 D.55:登上第1级:1种;登上第2级:2种;登上第3级:1+2=3种(前一步要么从第1级迈上来,要么从第2级迈上来);登上第4级:2+3=5种(前一步要么从第2级迈上来,要么从第3级迈上来);登上第5级:3+5=8种;登上第6级:5+8=13种;登上第7级:8+13=21种;登上第8级:13+21=34种,故选B.7.将数字1,2,3,4,填入表格内,要求每行、每列的数字互不相同,如图所示,则不同的填表方式共有()种A.432B.576C.720D.864,行交换共有A44=24种,列交换共有A44=24种,所以根据分步乘法计数原理得到不同的填表方式共有24×24=576种,故选B.8.(2019河北衡水模拟,14)从集合{1,2,3,4,…,10}中,选出5个数组成子集,使得这5个数中任意两个数的和都不等于11,则这样的子集有个.,将和等于11的放在一组:1和10,2和9,3和8,4和7,5和6.从每一小组中取一个,有C21=2种,共有2×2×2×2×2=32个.故选A.9.(2019内蒙古赤峰一模,14)某校从6名教师中选派3名教师去完成4项不同的工作,每人至少完成一项,每项工作由1人完成,其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案种数是.3名教师去完成4项不同的工作,每人至少完成一项,每项工作由1人完成,所以当3名教师确定时,则其中1人必须完成两项工作,故安排3名教师完成4项工作,可以先确定完成两项工作的1名人员,其方法有C31,然后再确定完成的工作,其方法有C42,然后再将剩下的两项工作分配给剩下的两人,其方法有C21,故当3名教师确定时,完成工作的方法有C31·C42·C21种.因为甲和乙不同去,甲和丙只能同去或同不去,故有三种方法选择教师,第一种方法:甲参加,乙不参加,丙参加,再从剩下的3人中选择1人,其方法有C31种,第二种方法:甲不参加,乙参加,丙不参加,再从剩下的3人中选择2人,其方法有C32种,第三种方法:甲不参加,乙不参加,丙不参加,再从剩下的3人中选择3人,其方法有C33种;故最终选派的方法为(C31+C32+C33)·C31·C42·C21=252.故选A.10.(2019福建宁德质检,14)中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同样长短的小木棍.如图,是利用算筹表示数1~9的一种方法.例如:137可表示为“”,26可表示为“”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用1~9这9个数字表示三位数的个数为.,当百位数为1时,十位数为1有2种,十位数为2有2种,十位数为3有2种,十位数为4有1种,为6有2种,为7有2种,为8有1种;当百位数为2时,十位数为1有2种,为2有2种,为3有1种,为6有2种,为7有1种;当百位数为3时,十位数为1有2种,十位数为2有1种,为6有1种;当百位数为4时,只有1种;当百位数为6时,十位数为1有2种,为2有2种,为3有1种,为6有2种,为7有1种;当百位数为7时,十位数为1有2种,为2有1种,为6有1种;当百位数为8,只有一种,一共有38种.综合提升组11.(2019江西南康中学模拟,7)任取集合{1,2,3,4,…,10}中三个不同数a1,a2,a3,且满足a2-a1≥2,a3-a2≥3,则选取这样的三个数的方法种数共有()A.27B.30C.35D.48,a3-a1=5,a1,a3的值有5种情况,则a2只有1种情况,共有5×1=5种情况;第二类,a3-a1=6,a1,a3的值有4种情况,则a2有2种情况,共有4×2=8种情况;第三类,a3-a1=7,a1,a3的值有3种情况,则a2有3种情况,共有3×3=9种情况;第四类,a3-a1=8,a1,a3的值有2种情况,则a2有4种情况,共有2×4=8种情况;第五类,a3-a1=9,a1,a3的值有1种情况,则a2有5种情况,共有1×5=5种情况;则选取这样的三个数方法种数共有5+8+9+8+5=35,故选C.12.把2支相同的晨光签字笔,3支相同的英雄钢笔,全部分给4名优秀学生,每名学生至少1支,则不同的分法有()A.24种B.28种C.32种D.36种,有一个人分到一支钢笔和一支签字笔,这种情况下的分法:先将一支钢笔和一支签字笔分给一个人,有4种分法,将剩余的2支钢笔, 1支签字笔分给剩余3名同学,有3种分法,共有3×4=12种不同的分法;第二类,有一个人分到两支签字笔,这种情况下的分法:先将两支签字笔分给一个人,有4种情况,将剩余的3支钢笔分给剩余3个人,只有1种分法,共有4×1=4种不同的分法;第三类,有一个人分到两支钢笔,这种情况的分法:先将两支钢笔分给一个人,有4种情况,再将剩余的两支签字笔和一支钢笔分给剩余的3个人,有3种分法,那共有3×4=12种不同的分法.综上所述,总共有12+4+12=28种不同的分法.故选B.13.现有红、黄、蓝、绿四个骰子,每个骰子的六个面上的数字分别为1,2,3,4,5,6.若同时掷这四个骰子,则四个骰子朝上的数字之积等于24的情形共有种(请用数字作答).24=6×4×1×1=6×2×2×1=4×3×2×1=3×2×2×2,对于上述四种情形掷这四个骰子时,分别有A42=12,C41×C32=12,A44=24,C41=4种情形,综上共有12+12+24+4=52种情形.14.(2019河南南阳一中模拟,14)如图,矩形的对角线把矩形分成A,B,C,D四部分,现用5种不同颜色给四部分涂色,每部分涂1种颜色,要求共边的两部分颜色互异,则共有种不同的涂色方法(用数字作答).,区域A有5种涂色方法;区域B有4种涂色方法;区域C的涂色方法可分2类:若C与A 涂同色,区域D有4种涂色方法;若C与A涂不同色,此时区域C有3种涂色方法,区域D也有3种涂色方法.所以共有5×4×4+5×4×3×3=260种涂色方法.15.(2019江苏泰州模拟,11)在冬奥会志愿者活动中,甲、乙等5人报名参加了A,B,C三个项目的志愿者工作,因工作需要,每个项目仅需1名志愿者,且甲不能参加A,B项目,乙不能参加B,C项目,那么共有种不同的志愿者分配方案.(用数字作答),乙都参加,则甲只能参加C项目,乙只能参加A项目,B项目有3种方法;若甲参加,乙不参加,则甲只能参加C项目,A,B项目,有A32=6种方法;若甲参加,乙不参加,则乙只能参加A项目,B,C项目,有A32=6种方法;若甲不参加,乙不参加,有A33=6种方法.根据分类计数原理,共有3+6+6+6=21种.创新应用组16.将数字“124470”重新排列后得到不同的偶数个数为()A.180B.192C.204D.264,分3种情况讨论:①个位数字为0,在前面5个数位中任选2个,安排2个数字4,有C52=10种情况,将剩下的3个数字全排列,安排在其他的数位,有A33=6种情况,则此时有10×6=60个偶数.②个位数字为2,0不能在首位,有4种情况,在剩下的4个数位中任选2个,安排2个数字4,有C42=6种情况,将剩下的2个数字全排列,安排在其他的数位,有A22=2种情况,则此时有4×6×2=48个偶数.③个位数字为4,0不能在首位,有4种情况,将剩下的4个数字全排列,安排在其他的数位,有A44=24种情况,则此时有4×24=96个偶数.共有60+48+96=204个不同的偶数.故选C.17.(2019江苏连云港模拟,14)已知x,y∈N+,满足1x −1y=12019,则所有数对(x,y)的个数是.因为1x −1y=12019,即2 019y-2 019x=xy,所以(x-2 019)(y+2 019)=-2 0192.因为已知x,y∈N+,所以y+2 019>0,x-2 019<0.又2 019=3×673,故有以下情况:若x-2 019=-3,y+2 019=673×2 019,得x=2 016,y=1 356 768,若x-2 019=-9,y+2 019=6732,得x=2 010,y=450 910,若x-2 019=-673,y+2 019=3×2 019,得x=1 346,y=4 038,若x-2 019=-1,y+2 019=2 0192,得x=2 018,y=2 019×2 018,即(x,y)的值共4个.18.如图,在由若干个同样小的平行四边形组成的大平行四边形内有一个★,则含有★的平行四边形共有个.(用数字作答)★的平行四边形的左上角的顶点有4种可能,右下角的顶点有12种可能.由一个左上角顶点和一个右下角顶点就能构成一个平行四边形,所以共有48个含有★的平行四边形.。

（5）分类加法计数原理与分步乘法计数原理1.某校高一年级有四个班，四位老师各教一个班的数学在该年级某次数学考试中，要求每位数学老师均不在本班监考，则不同的安排监考的方法种数为( )A.8B.9C.12D.242.从6人中选出4人参加某大学举办的数学、物理、化学、生物比赛，每人只能参加其中一项，且每项比赛都有人参加，其中甲、乙两人都不能参加化学比赛，则不同的参赛方案的种数为( )A.94B.180C.240D.2863.某同学有7本不同的书，其中语文书2本、英语书2本、数学书3本.现在该同学把这7本书放到书架上排成一排，要求2本语文书相邻、2本英语书相邻、3本数学书中任意2本不相邻，则不同的排法种数为( )A.12B.24C.48D.7204.旅游体验师小李受某网站邀请，决定在甲、乙、丙、丁这四个景区进行体验式旅游.已知他不能最先去甲景区旅游，不能最后去乙景区和丁景区旅游，则他可选的旅游路线数为( )A.24B.18C.16D.105.如图为我国数学家赵爽在为《周髀算经》作注时验证勾股定理的示意图，现提供5种颜色给其中5个小区域A，B，C，D，E涂色，规定每个区域只涂1种颜色，相邻区域颜色不相同，则不同的涂色方案共有( )A.120种B.260种C.340种D.420种6.已知从东、西、南、北四面通往山顶的路分别有2，3，3，4条，若要从其中面上山，从剩余三面中的任意一面下山，则不同的走法最多时应( )A.从东面上山B.从西面上山C.从南面上山D.从北面上山7.用1，2，3三个数字组成一个四位数，规定这三个数字必须都使用，且同一数字不能相邻出现，则这样的四位数有( )A.6个B.9个C.18个D.36个8.某体育彩票规定：从01至36共36个号中抽出7个号为一注，每注2元.某人想从01至10中选3个连续的号，从11至20中选2个连续的号，从21至30中选1个号，从31至36中选1个号组成一注，则这个人把这种特殊要求的号买全（每组号买一注），需要( )A.3360元B.6720元C.4320元D.8640元9.由中华人民共和国商务部和上海市人民政府主办的第三届中国国际进口博览会于2020年11月5日至10日在中国上海国家会展中心举办，本届进口博览会新设了公共卫生防疫、节能环保、智慧出行和体育用品及赛事等四大专区.将甲、乙、丙、丁等5名志愿者分派到新设的四个专区，要求每个新设的专区至少分到一人，则甲被分派到公共卫生防疫专区的分法种数为( )A.24B.36C.60D.7210.某旅行社共有5名专业导游，其中3人会英语，3人会日语，若在同一天要接待3个不同的外国旅游团，其中有2个旅游团要安排会英语的导游，1个旅游团要安排会日语的导游，则不同的安排方法种数有( )A.12B.13C.14D.1511.某新闻采访组由5名记者组成，其中甲、乙、丙、丁为成员，戊为组长.甲、乙、丙、丁分别来自A，B，C，D四个地区.现在该新闻采访组要到A，B，C，D四个地区去采访，在安排采访时要求：一地至少安排一名记者采访且组长不单独去采访；若某记者要到自己所在地区采访时必须至少有一名记者陪同.则所有采访的不同安排方法有___________种. 12.用数字0，1，2，3，4，5组成没有重复数字的四位数，其中百位上的数字是5的四位数共有___________个.（用数字作答）13.某栏目组在一节目中拿出两个信箱，信箱中放着观众的来信，甲箱中有30封，乙箱中有20封.现由主持人不放回地抽取来信，若先从两箱中抽取一封确定来信者为幸运之星，再从两箱中各抽取一封确定来信者为幸运观众，则有__________种不同的结果.14.有A，B，C三个城市，每天上午从A城去B城有5班汽车，2班火车，都能在12:00前到达B城，下午从B城去C城有3班汽车，2班轮船.某人上午从A城出发去B城，要求12:00前到达，下午从B城去C城，则不同的走法有__________种.15.从甲、乙、丙等10名学生中选派4人参加某项活动，若甲入选则乙一定入选，若甲不入选则丙一定入选，则共有_________种选派方案.答案以及解析1.答案：B解析：设四个班分别是A 、B 、C 、D ，对应的数学老师分别是a 、b 、c 、d.让a 老师先选，可从B 、C 、D 班中选一个，有3种选法，不妨假设a 老师选的是B ，则b 老师从剩下的三个班级中任选一个，有3种选法，剩下的两位老师都只有1种选法.由分步乘法计数原理，知共有33119⨯⨯⨯=种不同的安排方法.故选：B.2.答案：C解析：第一步，因为甲、乙两人都不能参加化学比赛，所以从剩下的4人中选1人参加化学比赛，共有4种选法；第二步，在剩下的5人中任选3人参加数学、物理、生物比赛，共有54360⨯⨯=种选法. 由分步乘法计数原理，得不同的参赛方案的种数为460240⨯=，故选：C.3.答案：C解析：先将2本语文书看成一个元素，2本英语书看成一个元素，然后排成一排，有22A 种不同的排法，再将3本数学书插到这2个元素形成的3个空隙中，有33A 种不同的排法，再排2本语文书，有22A 种不同的排法，最后排2本英语书，有22A 种不同的排法.根据分步乘法计数原理，得共有23222322A A A A 48=种不同的排法.故选C.4.答案：D解析：小李可选的旅游路线分两种情况：①最后去甲景区旅游，则可选的路线有33A 种；②不最后去甲景区旅游，则可选的路线有1222C A ⨯种.所以小李可选的旅游路线数为312322A C A 10+⨯=.5.答案：D解析：分四步：①区域A 涂色方案有5种；②区域B 涂色方案有4种；③区域C 涂色方案有3种；④对于区域D ，E ，若D 与B 颜色相同，则区域E 涂色方案有3种，若D 与B 颜色不同，则区域D ，E 涂色方案均有2种，所以区域D ，E 涂色方案共有3227+⨯=（种）.故不同的涂色方案有5437420⨯⨯⨯=（种）.故选D.6.答案：D解析：从东面上山，不同的走法共有2(334)20⨯++=（种）；从西面上山，不同的走法共有3(234)27⨯++=（种）；从南面上山，不同的走法共有3(234)27⨯++=（种）；从北面上山，不同的走法共有4(233)32⨯++=（种）.所以应从北面上山.故选D.7.答案：C解析：由题意，知1，2，3中必有某一个数字使用2次，第一步，确定谁被使用2次，有3种情况；第二步，把这2个相同的数字放在四位数不相邻的两个数位上，有3种情况；第三步，将余下的2个数字放在四位数余下的两个数位上，有2种情况.故符合题意的四位数有33218⨯⨯=（个）.故选C.8.答案：D解析：从01至10中选3个连续的号，有8种选法；从1l 至20中选2个连续的号，有9种选法；从21至30中选1个号，有10种选法；从31至36中选1个号，有6种选法.故总的选法有891064320⨯⨯⨯=（种），可得需要243208640⨯=（元）.故选D. 9.答案：C解析：若甲被单独分派到公共卫生防疫专区，则有2343C A 36=种分法，若甲没有被单独分派到公共卫生防疫专区，则有44A 24=种分法，根据分类加法计数原理可得，共有362460+=种分法.10.答案：C解析：由题意知有1名导游既会英语又会日语，记甲为既会英语又会日语的导游，按照甲是否被安排到需要会英语的旅游团可分为两类：第一类，甲被安排到需要会英语的旅游团，则可分两步进行：第一步，从会英语的另外2人中选出1人，有2种选法，将选出的人和甲安排到2个需要会英语的旅游团，有2种安排方法，所以有224⨯=种安排方法；第二步，从会日语的另外2人中选出1人安排到需要会日语的旅游团，共2种选法. 故此时共有428⨯=种安排方法；第二类，甲没有被安排到需要会英语的旅游团，则可分两步进行：第一步，将会英语的另外2人安排到需要会英语的旅游团，有2种安排方法；第二步，从会日语的3人（包括甲）中选出1人安排到需要会日语的旅游团，有3种选法.故此时共有236⨯=种选法.综上，不同的安排方法种数为8614+=.故选：C.11.答案：44解析：分两类：①甲，乙，丙，丁都不到自己的地区，组长可任选一地有()3311436⨯⨯⨯⨯=； ②甲，乙，丙，丁中只一人到自己的地区，并有组长陪同有()21148⨯⨯⨯=.所以总数36844+=.故答案为：44.12.答案：48解析：依题意，组成的没有重复数字的四位数的百位上的数字为5，分两步进行分析：①组成的四位数的千位上的数字不能为0，则千位上的数字有4种选法；②在剩下的4个数字中选出2个，分别安排在十位和个位上，不同的安排方法共有24A 12=（种）.则符合条件的四位数共有12448⨯=（个）.13.答案：28800解析：分两类：①当幸运之星在甲箱中抽取时，不同的结果有30292017400⨯⨯=（种）；②当幸运之星在乙箱中抽取时，不同的结果有20193011400⨯⨯=（种）.所以不同的结果共有174001140028800+=（种）.14.答案：35解析：由题意，知从A 城到B 城的走法有527+=（种）；从B 城到C 城的走法有325+=（种）.故不同的走法有7535⨯=（种）.15.答案：84解析：当甲入选时，乙一定入选，另外2人可从剩余的8人中选取，共有28C 种方案；当甲不入选时，丙一定入选，另外3人可从剩余的8人中选取，共有38C 种方案.根据分类加法计数原理，得选派方案共有233889C C C 84+==（种）.。

届高考人教B版数学一轮复习方案课时作业第55讲随机数与几2022年届高考人教B版数学一轮复习方案课时作业第55讲随机数与几何概型Word版含答案]课时作业(五十五) [第55讲随机数与几何概型](时间：35分钟分值：80分)基础热身1．在线段[0，3]上任投一点，则此点坐标小于1的概率为( ) 111A. B. D．1 2342．[2022年九江六校三联] 在一球内有一边长为1的内接正方体，一动点在球内运动，则此点落在正方体内部的概率为( )A.__ C. D.π2ππ3π3．[2022年大连4月测试] 一个路口的红绿灯，红灯的时间为30秒，绿灯的时间为40秒，黄灯的时间为5秒，当某人到达路口时看见的是红灯的概率是( )1234A. B. D. 55554．[2022年鸡西三模] 欧阳修《卖油翁》中写到：(翁)乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3 cm的圆，中间有边长为1 cm的正方形孔，若你随机向铜钱上滴一滴油，则油(油滴大小忽略不计)正好落入孔中的概率是( )A. 能力提升→→→5．已知P是△ABC所在平面内一点，PB＋PC＋2PA＝0，先向△ABC内随机掷点，则点落在△PBC内的概率是( ) 1121A. B. D. 43326．在区间(0，π]上随机取一个数x，则事件“sinx＋3c osx≤1”发生的概率为( ) 1112A. B. D. 432317．[2022年信阳二模] 在面积为S的△ABC内随机取一点M，则△MBC的面积S△MBC≤S2的概率为( )1123A. B. D.32349π94π4 C. D. 44π99π2022年届高考人教B版数学一轮复习方案课时作业第55讲随机数与几何概型Word版含答案]8．[2022年韶关调研] 已知Ω＝{(x，y)|x＋y≤6，x≥0，y≥0}，A＝{(x，y)|x≤4，y≥0，x－2y≥0}，若向区域Ω上随机投一点P，则点P落入区域A的概率为( )1214A. B. D. 99399．[2022年郑州一中质检] 在棱长为2的正方体ABCD－A1B1C1D1中，点O为底面ABCD的中心，在正方体ABCD－A1B1C1D1内随机取一点P，则点P到点O的距离大于1的概率等于________．x－4x≤0，2210．若不等式组－1≤y≤2，表示的平面区域为M，(x－4)＋y≤1表示的平面区域为x－y－1≥0N，现随机向区域M内抛一点，则该点落在平面区域N内的概率是________．11．[2022年琼海二模] 一只蚂蚁在边长为4的正三形内爬行，某时刻此蚂蚁距三角形三个顶点的距离均超过1的概率为________．12．(13分)某班主任统计本班50名学生放学回家后学习时间的数据，用条形图表示(如图K55－1)．(1)求该班学生每天在家学习时间的平均值；(2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话，求在学习时间为1 h的学生中选出的人数；(3)假设学生每天在家学习时间为18时至23时，已知甲每天连续学习2 h，乙每天连续学习3 h，求22时甲、乙都在学习的概率．2图K55－1难点突破13．(12分)设有关于x的一元二次方程x＋2ax＋b＝0.(1)若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率；(2)若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．222022年届高考人教B版数学一轮复习方案课时作业第55讲随机数与几何概型Word版含答案]课时作业(五十五)【基础热身】11．B [解析] 点坐标小于1的区间长度为132．D [解析] 由已知可得球的半径为r＝__π，球的体积为V＝π×＝，正方2322体体积V1＝1，所以概率P＝.故选D.V3π3．B [解析] 某人到达路口看到红灯的概率是P＝44．D [解析] 概率为P＝＝D.329ππ2【能力提升】→→→5．D [解析] 根据PB＋PC＋2PA＝0知，点P是△ABC的BC 边上中线的中点，故△PBC1的面积等于△ABC面积的D.2π π16．C [解析] 由sinx＋3cosx≤1得sin x≤，当x∈(0，π]x3 22 ππ－21≤π，所以所求概率为P＝＝.故选C.π－0212＝故选B.30＋40＋557．D [解析] 如图，点D，E分别是AB，AC的中点，连接DE，在阴影区域内任取一点1S四边形BCED3M，则有S△MBC≤S.所以所求概率P＝＝.故选D.2S△ABC4118．B [解析] 分别画出两个集合表示的区域可知SΩ＝×6×6＝18，SA＝×4×2＝4，22由几何概型概率计算可得P＝SA42，选B. SΩ189π22π9．1－[解析] 因为正方体的体积为8，而半球的体积为×1×π＝P__π8－3π到点O的距离大于1的概率为＝1－8122022年届高考人教B版数学一轮复习方案课时作业第55讲随机数与几何概型Word版含答案]ππ[解析] 如图所示：P＝. __×（1＋4）×3212π×1211．1－3π[解析] 如图，当蚂蚁在图示三个半径为1的扇形区域外时满足条件，241π23__1233π由几何概型公式得1－1－__4×2212．解：(1)平均学习时间为20×1＋10×2＋10×3＋5×4＝1.8 h.5010(2)20×＝4.50(3)设甲开始学习的时刻为x，乙开始学习的时刻为y，试验的全部结果所构成的区域为Ω＝{(x，y)|18≤x≤21，18≤y≤20}，面积SΩ＝2×3＝6.事件A表示“22时甲、乙正在学习”，所构成的区域为A＝{(x，y)|20≤x≤21，19≤y≤20}，面积为SA＝1×1＝1，这是一个几何概型，所以P(A)＝SA1＝. SΩ6[点评] 根据以上的解法，我们把此类问题的解决总结为以下四步：(1)设变量．从问题情景中，发现哪两个量是随机的，从而设为变量x，y.(2)集合表示．用(x，y)表示每次试验结果，则可用相应的集合分别表示出试验全部结果Ω和事件A所包含试验结果．一般来说，两个集合都是几个二元一次不等式的交集．(3)作出区域．把以上集合所表示的平面区域作出来，先作不等式对应的直线，然后取一特殊点验证哪侧是符合条件的区域．计算求解．根据几何概型的概率公式，易从平面图形中两个面积的比求得．【难点突破】13．解：设事件A为“方程x＋2ax＋b＝0有实根”．当a≥0，b≥0时，方程x＋2ax＋b＝0有实根的充要条件为a≥b.22222022年届高考人教B版数学一轮复习方案课时作业第55讲随机数与几何概型Word版含答案](1)基本事件共12个：(0，0)，(0，1)，(0，2)，(1，0)，(1，1)，(1，2)，(2，0)，(2，1)，(2，2)，(3，0)，(3，1)，(3，2)．其中第一个数表示a的取值，第二个数表示b的取值．93事件A中包含9个基本事件，事件A发生的概率为P(A)＝124(2)试验的全部结果所构成的区域为{(a，b)|0≤a≤3，0≤b≤2}．构成事件A的区域为{(a，b)|0≤a≤3，0≤b≤2，a≥b}．12。

课时标准练 53用样本估计总体根底稳固组1.(2021福建龙岩 4 月模拟 ,4)党的十八大以来,脱贫攻坚取得显著成绩.2021 年至 2021 年 4 年间 ,累计脱贫 5 564 万人 ,2021 年各地根据实际进行创新,精准、高效地完成了脱贫任务.某地区对当地 3 000户家庭的2021 年所有的年收入情况调查统计,年收入的频率分布直方图如下图,数据 (单位 :千元 )的分组依次为 [20,40),[40,60),[60,80),[80,100], 那么年收入不超过 6 万的家庭大约为()A.900 户B.600 户C.300 户D.150 户2.(2021湖南长郡中学一模,7)某赛季甲、乙两名篮球运发动各13 场比赛得分情况用茎叶图表示如图.根据上图 ,对这两名运发动的成绩进行比拟,以下四个结论中,不正确的选项是 ()A. 甲运发动得分的极差大于乙运发动得分的极差B.甲运发动得分的中位数大于乙运发动得分的中位数C.甲运发动的得分平均值大于乙运发动的得分平均值D.甲运发动的成绩比乙运发动的成绩稳定3.(2021四川成都考前模拟,3)某教育局为了解“跑团〞每月跑步的平均里程,收集并整理了至 2021 年 11 月期间“跑团〞每月跑步的平均里程(单位 :公里 )的数据 ,绘制了下面的折线图2021 年.1 月根据折线图 ,以下结论正确的选项是()A. 月跑步平均里程的中位数为 6 月份对应的里程数B.月跑步平均里程逐月增加C.月跑步平均里程顶峰期大致在8、9 月D.1 月至 5 月的月跑步平均里程相对于 6 月至 11 月 ,波动性更小 ,变化比拟平稳4.(2021山东、湖北冲刺二,3)当 5 个正整数从小到大排列时,其中位数为4,假设这6,那么这 5 个数的均值不可能为 ()5 个数的唯一众数为A.3 .65.(2021内蒙古呼和浩特一模,8)如图为某班35 名学生的投篮成绩面局部数据破损导致数据不完全.该班学生投篮成绩的中位数是哪一选项中的数值()(每人投一次 )的条形统计图,其中上5,那么根据统计图,无法确定以下A.3 球以下 (含 3 球 )的人数B.4 球以下 (含 4 球 )的人数C.5 球以下 (含 5 球 )的人数D.6 球以下 (含 6 球 )的人数6.(2021四省名校大三,6)某校李老本学期任高一 A 班、 B 班两个班数学教学,两个班都有50 名学生 ,下反映的是两个班在本学期 5 次数学中的班平均分比,根据表信息,以下不正确的是()A. A 班的数学成平均水平好于 B 班B.B班的数学成没有 A 班定C.下次 B 班的数学平均分高于 A 班D.在第一次考中 ,A、 B 两个班平均分78 分7.(2021四川达州四模,10)数据x1,x2,⋯,x10,2的平均2,方差1,数据x1,x2,⋯,x10相于原数据() A. 一定 B. 得比定C.得比不定D.定性不可以判断8.(2021江西景德盟校考二,4)某7个数的平均数4,方差 2,参加一个新数据4,此8 个数的平均数2,方差 s , ()A. = 4,s2= 2B. = 4,s2> 2C. = 4,s2 <2D. > 4,s2< 29.(2021山春季高考,24)在一批棉花中随机抽了500 根棉花的度并制了如所示的率分布直方,由可知 ,本中棉花的度大于是.(精确到 1 mm) 作本225 mm 的数,10.(2021广莞考前冲刺,13)本x1,x2,x3,⋯ ,x n的方差 s2= 2,本2x1 + 1,2x2+ 1,2x3+ 1,⋯ ,2x n+ 1 的方差.11.(2021河南天一大考三,15)一本数据按从小到大的序排列: -1,0,4,x,y,14,数据的平均数与中位数均 5,其方差.12.(2021北大附中五模,18)春市局某公司月收入在1 000~4000 元内的工行一次,并根据所得数据画出本的率分布直方 (每个分包括左端点 ,不包括右端点 ,如第一表示工月收入在区[1 000,1 500) 内 ,位 : 元 ).(1)估公司的工月收入在[1 000,2 000) 内的概率 ;(2)根据率分布直方估本数据的中位数和平均数.综合提升组13.(2021宁夏川一中三模,4)甲、乙两数据如茎叶所示,假设它的中位数相同,平均数也相同 ,中的 m,n 的比 =()A. B.14.(2021湖南衡阳二模,4)本x1,x2,⋯,x n的平均数x;本 y1,y2,⋯ ,y m的平均数 y(x≠y),假设本x1,x2,⋯ ,x n,y1,y2,⋯ ,y m的平均数 z=ax+ (1-a)y,其中 0<a<, n,m(n,m∈N* )的大小关系()A. n=mB. n≥ mC.n<mD.n>m15.(2021安徽太和中学一模,16)本数据a1,a2,a3,a4,a5的方差 s2=-20),本数据2a1+ 1,2a2+ 1,2a3+ 1,2a4+ 1,2a5+ 1 的平均数.16.(2021新疆吾自治区二模,19)某市有甲、乙两位航模运参加了国家集,分从他在集期参加的假设干次成中随机抽取8 次 ,如下 :甲:8281797895889384乙:9295807583809085(1)画出甲、乙两位学生成的茎叶,指出学生乙成的中位数;(2)要从中派一人参加国比,从平均成和方差的角度考,你派哪位学生参加适宜?明理由 .创新应用组17.(2021云南昆明二模,4)“搜索指数〞是网民通搜索引擎,以每天搜索关的次数基所得到的指 .“搜索指数〞越大 ,表示网民关的搜索次数越多,关相关的信息关注度也越高 .下是 2021 年 9 月到 2021 年 2 月半年中 ,某个关的搜索指数化的走.根据走 ,以下正确的选项是()A. 半年中 ,网民关相关的信息关注度呈周期性化B.半年中 ,网民关相关的信息关注度不断减弱C.从网民关的搜索指数来看,去年 10 月份的方差小于11 月份的方差D.从网民关的搜索指数来看,去年 12 月份的平均大于今年 1 月份的平均18.(2021河北衡水模三,19)“日行一万步 ,健康你一生〞的养生念已深入人心,由于研究性学的需要 ,某大学生收集了“微信运〞中特定甲、乙两个班n 名成一天行走的步数,然后采用分抽的方法按照[20,30),[30,40),[40,50),[50,60) 分抽取了20 名成的步数,并制了如下尚不完整的茎叶(位 :千步 ):甲、乙两班行走步数的平均都是44千步 .(1) 求 x,y 的 ;(2) ①假设 n= 100,求甲、乙两个班②假设估中一天行走步数少于100 名成中行走步数在40 千步的人数比于[20,30),[30,40),[40,50),[50,60) 各的人数[40,50) 千步的人数少12 人 ,求 n 的 .;课时标准练 53 用样本估计总体1.A 由 率分布直方 可得年收入不超 6 万的家庭的概率 (0.005+ 0.01)×20= 0.3,所以年收入不 超 6 万的家庭数大 3 000×0.3= 900( ),故 A .2.D 由茎叶 知甲的极差 47-18=29,乙的极差是33-17=16,A 正确 ;甲中位数是 30,乙中位数是26,B 正确 ;甲均 29 ,乙均 25,C 正确 ;只有 D 不正确 ,甲的方差大于乙的方差 , 是乙成定 ,故 D.3.D 由折 知 ,月跑步平均里程的中位数 5 月份 的里程数 ;月跑步平均里程不是逐月增加的;月跑步平均里程顶峰期大致在9、 10 月份 ,故 A,B,C ,故 D. 4.A 五个数从小到大 a 1,a 2,a 3,a 4,a 5 ,依 意得 a 3= 4,a 4=a 5= 6,a 1 ,a 2 是 1,2,3 中两个不同的数 ,符合 意的五个数可能有三种情形:“1,2,4,6,6〞,“1,3,4,6,6〞,“2,3,4,6,6〞,其平均数分 3.8,4,4.2.均 不可 能 3.6,故 A . 5.C 因 共有 35 人,而中位数 是第 18 个数 ,所以第 18 个数是 5,从 中看出第四个柱状 的 范 在 6 以上 ,所以投 4 个球的有 7 人.可得 3 球以下 (含 3 球 )的人数 10 人 ,4 球以下 (含 4 球 )的人数10+ 7= 17(人 ),6 球以下 (含 6 球 )的人数 35-1= 34(人 ).故只有 5 球以下 (含 5 球 )的人数无法确定 ,故 C.6.C A 班的 5 次数学 平均分分 81,78,81,80,85,5 次的平均分(81+78+ 81+ 80+ 85)= 81,B班的 5 次数学 平均分分 75,80,76,85,80,5 次的平均分(75+ 80+ 76+ 85+ 80)= 79.2,A 班的数学平均分好于 B 班 ,A 正确 ;由于 A 班的成 都在 80 分附近 ,而 B 班的平均分 化很大 ,所以A 班成 定些 ,B 正确 ; 下次考 A,B 班的平均分不能 料 ,所以 C;在第一次考 中 ,平均分=78分,D 正确 .故 C.7.C由 可得 :⋯ = 2,所以 x 1+x 2 + ⋯ +x 10= 20,所以平均2,由- - ⋯---- ⋯ -= 1 得= 1.1>1,所以 得不 定 ,故 C.8.C根据 意有2-< 2,故 C.= 4,而 s =9.235 因 度大于225 mm 的 率 (0.004 4+ 0.005 0)×50= 0.47,所以 度大于 225 mm 的 数是 ×500= 235.10.82由 意 , 本数据 x 1,x 2,x 3,⋯,x n 的方差 s 2= 2, 本 2x 1+ 1,2x 2 +1,2x 3+ 1,⋯,2x n + 1 的方差 , = 2 22×s = 2 ×2= 8. -11∵-1,0,4,x,y,14 的中位数 5, = 5, ∴ ∴ = 5,即 y= 7,x= 6, 数据的平均数是 可得 数据的方差是 (36+ 25+ 1+ 1+ 4+ 81)= ,故答案12.解 (1) 工月收入在 [1 000,2 000) 内的概率 (0.000 2+ 0.000 4)×500= 0.3.(2)根据条件可知 ,从左至右小矩形的面 分 是 0.1,0.2,0.25,0.25,0.15,0.05,因此 ,中位数的估2 000+ = 2 400;平均数的估 1 250×0.1+ 1 750×0.2+ 2 250×0.25+2 750×0.25+3250×0.15+ 3 750×0.05= 2 400.上可知 ,中位数和平均数的估 都是2 400.13.A由 意得 ,甲 数据 :24,29,30 +m,42;乙 数据 :25,20+n ,31,33,42,∴甲、乙两 数据的中位数分、 31,且甲、乙两 数的平均数分甲乙由 意得解得,故 A.14.C由 意得z=(nx+my )=x+1-y,∴a=∵0<a< ,∴0< ,∴n<m.故 C.15.5 或 -3 本数据的平均数a, 方差s2=--2aa i+a 2)=- 2a a i+ 5a2) =-2a×5a+ 5a2)=-5a2).结合 s2=-20)可得 5a2= 20,∴a= ±2,即样本数据2 或 -2,那么样本数据2a1+ 1,2a2+ 1,2a3+ 1,2a4+ 1,2a5+1 的平均数为2×2+ 1= 5 或16.解(1)茎叶图如下:a1,a2 ,a3,a4,a5的平均数为2×(- 2)+1=- 3.∴学生乙成绩的中位数为84.(2)派甲参加比拟适宜,理由如下 :甲(70×2+ 80×4+ 90×2+ 9+ 8+ 8+ 4+ 2+ 1+ 5+ 3)= 85,乙(70×1+ 80×4+ 90×3+ 5+ 3+ 5+ 2+ 5)=85,甲[(78 -85)2+ (79- 85)2+ (81-85)2+ (82-85)2+ (84-85)2+ (88-85)2+ (95-85)2 + (93-85) 2]= 35.5,乙[(75 -85)2+ (80- 85)2+ (80-85)2+ (83-85)2+ (85-85)2+ (90-85)2+ (92-85)2 + (95-85) 2]= 41,因为甲乙甲乙 ,∴甲的成绩比拟稳定 ,派甲参加比拟适宜 .17.D根据走势图可知,这半年中,网民对该关键词相关的信息关注度不呈周期性变化,A 错;这半年中 ,网民对该关键词相关的信息关注度增减不确定,B 错 ;从网民对该关键词的搜索指数来看,去年 10 月份的搜索指数的稳定性小于11 月份的搜索指数的稳定性,所以去年 10 月份的方差大于11 月份的方差,C 错 ;从网民对该关键词的搜索指数来看,去年 12 月份的平均值大于今年 1 月份的平均值 ,D 正确 .应选 D.18.解(1)因为甲班的平均值为44,所以甲(26+ 32+ 42+ 40+x+ 45+ 46+ 48+ 50+ 52+ 53)= 44,解得 x=6.同理 ,因为乙班平均值为44,所以乙(26+ 34+ 30+y+ 41+ 42+ 46+ 50+ 52+ 57+ 58)= 44,解得 y=4.(2)①因为抽样比为,且抽取的20 名成员中行走步数在 [20,30),[30,40),[40,50),[50,60) 各层的人数依次为2,3,8,7,所以甲、乙两个班级100 名成员中行走步数在 [20,30),[30,40),[40,50),[50,60) 各层的人数依次为10,15,40,35.②该团队中一天行走步数少于40 千步的频率为,处于 [40,50) 千步的频率为,那么估计该团队中一天行走步数少于40 千步的人数与处于 [40,50) 千步的人数的频率之差为又因为该团队中一天行走步数少于40 千步的人数比处于 [40,50) 千步的人数少 12 人 ,所以 n= 12,解得 n= 80.。

2020届一轮复习人教B版计数原理课时作业1、若的展开式中的系数为，则（）A． B． C． D．2、在展开式中的常数项为A．1 B．2 C．3 D．73、已知展开式中，各项系数的和与其各项二项式系数的和之比为，则等于（）A．B．C．D．4、在的二项展开式中，若第四项的系数为，则（）A． B． C． D．5、若的展开式中的系数为8，则_____________．6、名同学参加班长和文娱委员的竞选，每个职务只需人，其中甲不能当文娱委员，则共有_____种不同结果（用数字作答）7、若，则__________．8、在411xx⎛⎫--⎪⎝⎭的展开式中，常数项为__________．9、已知的展开式中各项的二项式系数之和为128，则其展开式中含项的系数是______结果用数值表示10、如果的展开式中只有第4项的二项式系数最大，那么展开式中的所有项的系数之和是______．11、有3名女生和5名男生，按照下列条件排队，求各有多少种不同的排队方法？名女生排在一起；名女生次序一定，但不一定相邻；名女生不站在排头和排尾，也互不相邻；每两名女生之间至少有两名男生；名女生中，A，B要相邻，A，C不相邻．12、已知，．当时，求的值；当时，是否存在正整数n，r，使得、、，依次构成等差数列？并说明理由；当时，求的值用m表示．13、已知（1）求及的值；（2）求证：（），并求的值.（3）求的值.14、有3名男生，4名女生，在下列不同要求下，求不同的排列方法总数（用数字作答）．（1）全体排成一行，其中男生甲不在最左边；（2）全体排成一行，其中4名女生必须排在一起；（3）全体排成一行，3名男生两两不相邻.参考答案1、答案：D由题意二项式的展开式为，展开式的为，所以，解得，故选D.2、答案：D求出展开项中的常数项及含的项，问题得解。

【详解】展开项中的常数项及含的项分别为：,，所以展开式中的常数项为：.故选：D本题主要考查了二项式定理中展开式的通项公式及转化思想，考查计算能力，属于基础题。