当前位置：文档之家 › 现代控制理论习题解答(第四章)

现代控制理论习题解答(第四章)

  • 格式：docx
  • 大小：117.47 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

现代控制理论第四章答案

现代控制理论第四章答案

G T PG P Q 1 3 1 P11 3 2 0 P 12 0 3 0 P13 P12 P22 P23 P13 1 3 0 P11 P23 3 2 3 P12 P33 1 0 0 13
P 12 P22 P23
19 1 0, 2 0, 3 0 78
19 78 P 13 10 P23 39 P33 1 2
10 39 49 78 19 13
0 0 0 P11 P12 P13 1 0 0 0 P P k P k 2 / 4 P P k / 2 P P P 0 0 0 11 13 33 12 23 12 22 23 0 P13 P23 P33 0 0 0 P12 P23 k / 2 P22
P 12 P22
P 1 1 1 0 12 2 3 0 1 P22
7 P 11 4 5 P 12 8 9 P22 24
2 P 4 P 1 11 12 P 4 P 2 P22 0 11 12 2 P 6 P 1 22 12
1 2 19 13 123 76
故:矩阵P是负定的,所以系统的平衡状态是不稳定的
【习题4－8 】设线性离散系统的状态方程为
0 1 0 x(k 1) 0 0 1 x(k ) 0 k / 2 0
1 Q 0 0 0 0 0 P 11 P P 12 P 13
I A
a11
a12
a21 a22 (a22 a11 a12 a21 ) 1 2 0 2 (a11 a22 ) 1 2 0 2

现代控制理论答案第三版

现代控制理论答案第三版

解：由图，令 i1
= x1 , i2 = x 2 , u c = x3 ，输出量 y = R2 x 2 x1 = − x2 = − x3 = −
• • •
R1 x1 + L1 x1 + x3 = u
有电路原理可知： L2
•
R1 1 1 x1 − x3 + u L1 L1 L1 R2 1 x2 + x3 L2 L2
−1
⎡0 ⎢b ⎢ 1 ⎢0 ⎢ ⎣0
0⎤ 0⎥ ⎥ 0⎥ ⎥ b2 ⎦ 0 0 s a4 0⎤ a6 ⎥ ⎥ − 1⎥ ⎥ a3 ⎦
−1
−1 ⎡s ⎢a s + a 1 Wuy ( s ) = C ( sI − A) −1 B = [1 0 1 0]⎢ 2 ⎢− 1 0 ⎢ a5 ⎣0
1-5 系统的动态特性由下列微分方程描述
1 0 ⎤ ⎡ p13 ⎤ ⎡ 0 ⎡ p13 ⎤ ⎢ ⎥ ⎢ ⎥ 当 λ1 = −3 时， 3 0 2 p23 = −3⎢ p23 ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢− 12 − 7 − 6⎦ ⎥⎣ ⎢ p33 ⎦ ⎥ ⎢ p33 ⎦ ⎥ ⎣ ⎣
解得：
p23 = −3 p13 , p33 = 3 p13
⎡0 ⎢b ⎢ 1 ⎢0 ⎢ ⎣0
0⎤ 0⎥ ⎥ 0⎥ ⎥ b2 ⎦
(2) y + 5 y + 7 y + 3 y = u + 3 u + 2u
列写其相应的状态空间表达式，并画出相应的模拟结构图。 解：令
. ..
K
..
.
..
.
x1 = y ， x 2 = y ， x 3 = y
，则有
⎡ 。⎤ 1⎥ 1 0 ⎤ ⎡ x1 ⎤ ⎡0⎤ ⎡0 ⎢x 。 ⎢ ⎥ ⎢ ⎥ ⎢x ⎥ = ⎢ 0 0 1⎥ 2 ⎥ ⎢ x 2 ⎥ + ⎢0 ⎥ u ⎢。 ⎥ ⎢ ⎢ x3 ⎥ ⎢ ⎣− 3 − 7 − 5⎥ ⎦⎢ ⎣ x3 ⎥ ⎦ ⎢ ⎣1 ⎥ ⎦ ⎢ ⎦ ⎥ ⎣ ⎡ x1 ⎤ ⎥ y = [2 3 1]⎢ ⎢ x2 ⎥ ⎢ ⎣ x3 ⎥ ⎦

现代控制理论第4章测验参考答案

现代控制理论第4章测验参考答案

第4章测验题（共3题，时间：30分钟）1、若系统的齐次状态方程为),(t x f x= ，若存在状态矢量x e ，对于所有t ，都使x e 称为系统的平衡状态。

2、若二次型标量函数V (X )=V (x 1，x 2)=22212125x x x x ++, 若写成V (X )= X T PX 的形式（P 为对称阵），则PP 的符号性质为：。

3、系统状态空间表达式为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=013502 ，[]x y 11-=， （1）判断系统在平衡状态处的稳定性。

（2）分析系统的输出稳定性。

解：（1）令0=x ，易知该系统具有唯一一个平衡点为⎥⎦⎤⎢⎣⎡=00e x 。

设⎥⎦⎤⎢⎣⎡=22121211p p p p P ，取Q=I ，解李亚普诺夫方程PA+A T P=－I ，可得：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=61656537P 易知矩阵P 的符号性质为不定，所以系统在平衡点处不是渐近稳定的。

也可取⎥⎦⎤⎢⎣⎡=1000Q 为半正定阵，则22)(x Qx x x V T =-= ，易证明仅当x=0时0)(≡x V，因此Q 的选取合理。

解李亚普诺夫方程PA+A T P= －Q 求出⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=6165651225P ，P 阵符号也为不定，故系统在平衡点处不是渐近稳定的，但无法判断系统是李亚普诺夫意义稳定还是不稳定。

说明：通过第一方法可求得系统的特征值为2和－3，存在具有正实部的特征值，因此系统是不稳定的。

此外，通过求解该系统的自由解可知⎥⎦⎤⎢⎣⎡-+=-t t te x x e x e x t x 31020210210)()(，易知系统的状态是发散的，故系统是不稳定的。

（2）对于系统的输入输出稳定性分析：系统传递函数为31)3)(2()2()()(1+=+--=-=-s s s s B A sI C s G ， 唯一极点为-3，位于s 平面左半平面，因此系统为输出稳定。

现代控制理论习题解答(第四章)

现代控制理论习题解答(第四章)

第四章 控制系统的稳定性3-4-1 试确定下列二次型是否正定。

(1)3123212322212624)(x x x x x x x x x x v --+++= (2)232123222126410)(x x x x x x x x v ++---= (3)312321232221422410)(x x x x x x x x x x v --+++= 【解】： （1）04131341111,034111,01,131341111<-=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数不定。

(2)034101103031,0110331,01,4101103031<-=--->=--<-⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=P二次型函数为负定。

(3)017112141211003941110,010,1121412110>=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数正定。

3-4-2 试确定下列二次型为正定时，待定常数的取值范围。

312321231221211242)(x x x x x x x c x b x a x v --+++=【解】：312321231221211242)(x x x x x x x c x b x a x v --+++=x c b a x T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1112121110212111,011,0111111>---->>c b a b aa 满足正定的条件为：⎪⎩⎪⎨⎧++>+>>1111111114410ca b c b a b a a3-4-3 试用李亚普诺夫第二法判断下列线性系统的稳定性。

;1001)4(;1111)3(;3211)2(;1110)1(x x x x x x x x ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=【解】： （1）设22215.05.0)(x x x v +=⎩⎨⎧≠≤==-=--=+=)0(0)0(0222221212211)(x x x x x x x x x x x x x v为半负定。

现代控制理论课后习题答案

现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解：()()22232321s s s s s s s++ =++ ? ?D S N S ； ()3r 2,1,2E -：223381s s s s s s ??++ ?-- ? ???；()3r 2,3,3E ：223051s s s s s ??++ ?- ? ???；()3r 1,3,2E s --：01051s s ?? ?- ? ；()3r 2,1,5E s -：01001s ?? ?；()3r 3,1,1E -：01000s ?? ? ? ???；()1r 2,3E ：01000s ?? ? ? ???；()1r 1,2E ：00100s ?? ?；所以⼀个gcrd 为001s ??；取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。

1.9 求转移矩阵t A e (1)已知1141??=A ，根据拉⽒反变换求解转移矩阵tA e 。

(2) 已知412102113-?? ?= ? ?-??A ，根据C-H 有限项展开法求解转移矩阵t A e 。

解：(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -，得1,233,1λλ== 对1,23λ=，可以计算1,2()2rank λ=A I -，所以该特征值的⼏何重数为1。

《现代控制理论》第三版_.习题答案

《现代控制理论》第三版_.习题答案
或者
1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ； 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1－5. 根据微分方程， 写状态方程， 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法： 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1

现代控制理论第4章答案

现代控制理论第4章答案

现代控制理论第四章习题答案4-1判断下列二次型函数的符号性质：（1）222123122313()31122Q x x x x x x x x x x =---+-- （2）222123122313()4262v x x x x x x x x x x =++---解：（1）由已知得[]11231231232311232311()31122111113211112x Q x x x x x x x x x x x x x x x x x x ⎡⎤⎡⎤⎢⎥=-+------⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎡⎤⎢⎥--⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥---⎣⎦110∆=-<，2112013-∆==>-，31111711302411112--∆=--=-<--- 因此()Q x 是负定的 （2）由已知得[][]112312312323112323()433111143131x Q x x x x x x x x x x x x x x x x x x ⎡⎤⎢⎥=---+---+⎢⎥⎢⎥⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦110∆=>，2113014-∆==>-，3111143160131--∆=--=-<--因此()Q x 不是正定的 4-2已知二阶系统的状态方程：11122122a a xx a a ⎛⎫= ⎪⎝⎭试确定系统在平衡状态处大范围渐进稳定的条件。

解：方法（1）：要使系统在平衡状态处大范围渐进稳定，则要求满足A 的特征值均具有负实部。

即：111221222112211221221()0a a I A a a a a a a a a λλλλλ---=--=-++-= 有解，且解具有负实部。

即：1122112212210a a a a a a +<>且方法（2）：系统的原点平衡状态0e x =为大范围渐近稳定，等价于T A P PA Q +=-。

《现代控制理论》课后习题答案4

《现代控制理论》课后习题答案4

ε 和初始时刻 t0 有关)， 使得从球域 S (δ ) 内任一初始状态出发的状态轨线始终都保持在球域 则平衡状态 xe = 0 称为是李雅普诺夫意义下稳定的。 进一步， 如果平衡状态 xe = 0 S (ε ) 内，
是李雅普诺夫意义下稳定的，并且当 t → ∞ 时，始于原点邻域中的轨线 x (t ) → 0 ，则平衡 状态 xe = 0 称为在李雅普诺夫意义下是渐近稳定的。 它既适用于线性系统， 也适用于非线性系统， 既适用于时变系统， 也适用于时不变系统， 既适用于连续系统，也适用于离散系统。 4.4 怎样判别二次型函数的正定、负定、半正定、半负定？ 答：二次型函数的一般表达式为：
2 2 2
（2） V ( x ) = − x12 − 10 x 2 2 − 4 x3 2 + 6 x1 x2 + 2 x3 x2 ； （3） V ( x ) = 10 x1 + 4 x2 + x3 + 2 x1 x2 − 2 x3 x2 − 4 x1 x3
2 2 2
2 2 答： （1） V ( x ) = x12 + 4 x2 + x3 + 2 x1 x2 − 6 x2 x3 − 2 x1 x3
⎛ ⎡10 1 −2 ⎤ ⎞
由于矩阵 P 的三个顺序主子式分别是
⎛ ⎡10 1 ⎤ ⎞ ⎜⎢ ⎥⎟ Δ1 = 10 > 0 ， Δ 2 = det ⎜ ⎢ ⎟ = 39 > 0 ， Δ 3 = det ⎜ ⎢ 1 4 −1⎥ ⎟ = 17 > 0 ⎥ ⎝ ⎣ 1 4⎦ ⎠ ⎜ ⎢ −2 − 1 1 ⎥ ⎟ ⎦⎠ ⎝⎣
AT P + PA = −Q
其中，未知对称矩阵具有以下形式
⎡P P = ⎢ 11 ⎣P 12

《现代控制理论》第三版 第四章.习题答案

《现代控制理论》第三版 第四章.习题答案
1 x1， 2 x2 不对。
a11 a22 0
4-3（1）选 v( x ) x1 x2 ，平衡点 xe 0 v( x ) 0 ( x ) 2 x12 6 x2 2 6 x1 x2 x T Px v
2 3 P 3 6 2 3 0
1 P 11 0
4-2 法一： 系统的特征方程为：
I A 2 a11 a22 a11a22 a12 a21
系统大范围渐近稳定等价于方程有两个 负实部的共轭复特征值或两个负实特征 值，于是可以得到 1 2 a11 a22 0 12 a11a22 a12 a21 0 法二： P11 P12 设对称阵 P = ，设 Q I P12 P22
2
2
因为 i 为奇数 i 0 i 为偶数 i 0 ，所以
P 负定。
( x ) 0 渐近稳定 v 当 x 近稳定 或按
AT P PA Q
v( x ) 所以大范围渐
取Q I
7 4 P 5 8
稳定
5 8 3 8
1 0 2 0 所以 P 渐近
（2） v( x ) x1 x2
2
2
( x ) 2( x12 x2 2 ) 0 v
当
x v( x ) 所以大范围渐近稳定 1 2 P 0 0 1 2
2 2
或按 AT P PA Q
问题： 4-2 讨论对取 v( x ) x1 x2 ，
1 1 0
3 17.75 0 ，所以 Q( x )
是负定的
2） Q( x ) x T Px
1 1 1 P 1 4 3 1 3 1 1 1 0 2 3 0 所以 Q( x ) 不定符号

(完整word版)《现代控制理论》第3版课后习题答案

(完整word版)《现代控制理论》第3版课后习题答案

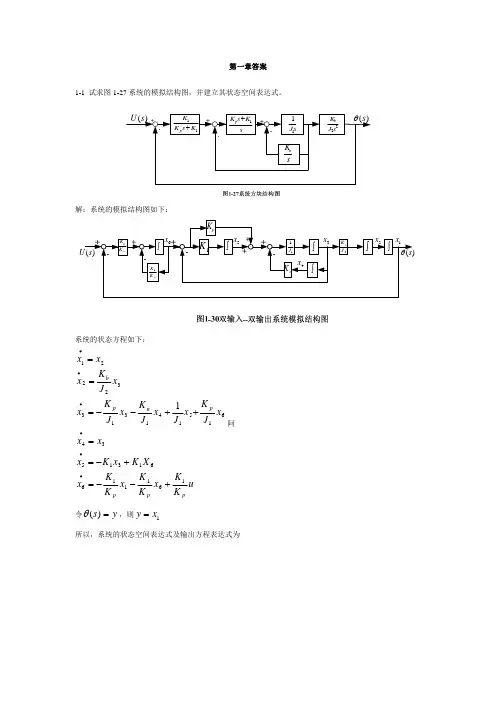
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

现代控制工程基础第四章习题解答

现代控制工程基础第四章习题解答

jω
0
σ
jω
0
σ
6
4.3 设单位负反馈开环传递函数如下，试概略绘出响 应的闭环根轨迹
(2) 解：
G ( s ) = K ( s + 1) s (2 s + 1)
G(s) = K *(s +1) , K * = 0.5K s(s + 0.5)
开环零点： z1 = −1, m = 1
开环极点： p1
= 0,
+1)π
θpx =19.48D
10
jω
19.48o
σ
0
11
4.6 设系统开环传递函数如下，试画出b从零到无穷变 化时的根轨迹。
(1)
G(s) =
20
(s + 4)(s + b)
解： 闭环系统特征方程： D(s) = s2 + 4s + 20 + b(s + 4) = 0
等效单位负反馈开环传递函数：G* (s)
K −1.1ω2 + ⎣⎡ω − 0.1ω3 ⎦⎤ j = 0
令实部、虚部等于零，可得：
⎧ω = 0
⎨⎩K = 0 ,
⎧⎪ω = ± 10
⎨ ⎪⎩K
=
11
显然产生开环虚根的开环增益K=11. 9
4.5 设试绘制下列多项式方程的根轨迹。
(1) s 3 + 2 s 2 + 3 s + K s + 2 K = 0
=
b(s + 4) s2 + 4s + 20
jω
开环零点：z1 = −4, m = 1
开环极点：p1,2 = −2 ± 4 j, n = 2

大连理工大学 现代控制理论 王金城 第四、五章 答案

大连理工大学 现代控制理论 王金城 第四、五章 答案

第四章习题参考答案4-1(1)211P 130101-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,,123212061506132013-∆=>∆==-=>∆=--=>-∴V(x)为正定的（2）841P 421111-⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,,12380020∆=>∆=∆-<∴V(x)为不定的4-2 ∵12x x 0==，∴e x 是系统的唯一平衡状态()3112211V x 4x x 2x x 42=⋅⋅+⋅⋅⋅ 31122x x x x =⋅+⋅ 22x =- 半负定 ∴系统在原点处的平衡状态是稳定的 ∴()421211V x x x 42=+可成为系统的李氏函数。

4-3（1）1122xx 21xx 04--⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ ,1212xx 0x 0x 0==⇒== ∴e x 是系统的平衡状态 设李氏函数为()T V x x Px =，TA P PA I +=-1112111212221222P P P P 202110P P P P 140401----⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 得11424P 1132496⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦,()2121113100449624∆=>∆=⋅-> ∴P 是正定的，系统在原点处的平衡状态是渐进稳定的。

李氏函数为()T221253V x x Px x x 2432==+用李氏第一方法校核,21221I A 67303004λλλλλλλ+-==++⇒=-+<=-+ ∴系统在原点处的平衡状态是渐进稳定的（2）112233x200x x 010x x 101x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦设李氏函数为()T V x x Px =，T A P PA I +=-111213111213122223122223132333132333201P P P P P P 200100010P P P P P P 010010001P P P P P P 101001---⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⇒-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦∴110361P 00211062⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,,1235110003672∆=>∆=>∆=>∴P 阵是正定阵，系统在原点处的平衡状态是渐进稳定的。

《现代控制系统理论》第3版课后习题问题详解

《现代控制系统理论》第3版课后习题问题详解

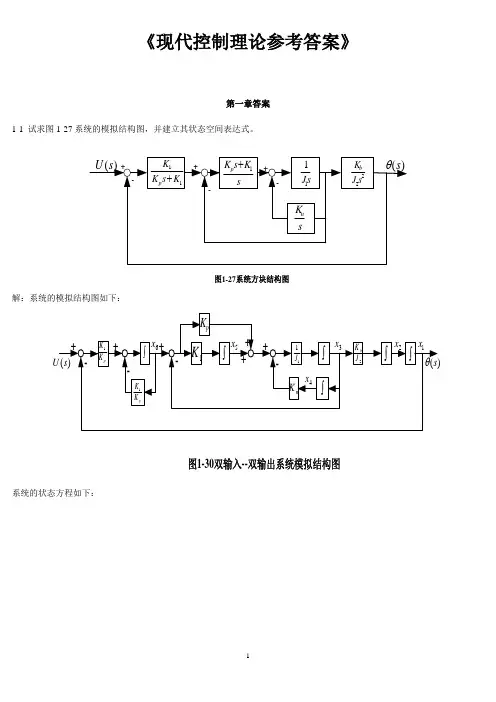
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，如此1x y =所以，系统的状态空间表达式与输出方程表达式为1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得2221332222213*********1x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：1-4 两输入1u ，2u ，两输出1y ，2y 的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。

解：系统的状态空间表达式如下所示： 1-5系统的动态特性由如下微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令..3.21y x y x y x ===，，，如此有 相应的模拟结构图如下： 1-6 〔2〕系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定如下状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘（1） 画出其模拟结构图（2） 求系统的传递函数 解：〔2〕⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求如下矩阵的特征矢量〔3〕⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解：A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得：3,2,1321-=-=-=λλλ当11-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得： 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 〔或令111-=p ，得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 〕 当21-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得： 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P〔或令112=p ，得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P 〕 当31-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得： 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将如下状态空间表达式化成约旦标准型〔并联分解〕〔2〕⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果 解：〔1〕串联联结 〔2〕并联联结1-11 〔第3版教材〕如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-11〔第2版教材〕 如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-12 差分方程为试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为〔1〕⎥⎦⎤⎢⎣⎡=11b 解法1： 解法2：求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以⎥⎦⎤⎢⎣⎡-=1011T所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。

现代控制理论习题解答(第四章)

现代控制理论习题解答(第四章)

第四章 控制系统的稳定性3-4-1 试确定下列二次型是否正定。

(1)3123212322212624)(x x x x x x x x x x v --+++= (2)232123222126410)(x x x x x x x x v ++---= (3)312321232221422410)(x x x x x x x x x x v --+++= 【解】： （1）04131341111,034111,01,131341111<-=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数不定。

(2)034101103031,0110331,01,4101103031<-=--->=--<-⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=P 二次型函数为负定。

(3)017112141211003941110,010,1121412110>=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数正定。

3-4-2 试确定下列二次型为正定时，待定常数的取值范围。

312321231221211242)(x x x x x x x c x b x a x v --+++=【解】：312321231221211242)(x x x x x x x c x b x a x v --+++=x c b a x T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1112121110212111,011,0111111>---->>c b a b a a 满足正定的条件为：⎪⎩⎪⎨⎧++>+>>1111111114410ca b c b a b a a3-4-3 试用李亚普诺夫第二法判断下列线性系统的稳定性。

;1001)4(;1111)3(;3211)2(;1110)1(x x x x x x x x ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=【解】： （1）设22215.05.0)(x x x v +=⎩⎨⎧≠≤==-=--=+=)0(0)0(0222221212211)(x x x x x x x x x x x x x v为半负定。

现代控制理论第四章习题答案

现代控制理论第四章习题答案

第4章“线性系统的能控性与能观性”习题与解答4.1 判断下列系统的能控性。

1) u x x x x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡10 01112121 2) ⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡21321321111001342100010u u x x x x xx3) ⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡21321321020011 10030013u u x x x x xx解：1) 由于该系统控制矩阵⎥⎦⎤⎢⎣⎡=01b ，系统矩阵⎥⎦⎤⎢⎣⎡=0111A ，所以 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=1101 0111Ab 从而系统的能控性矩阵为[]⎥⎦⎤⎢⎣⎡==1011Ab bU C 显然有[]n Ab bU C ===2rank rank满足能控性的充要条件，所以该系统能控。

2)由于该系统控制矩阵为100111B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=342100010A 则有，0101001001 01112431117AB ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦ 20100111001 111724317115A B -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦从而系统的能控性矩阵为21001110111171117115C U BABA B -⎡⎤⎢⎥⎡⎤==--⎣⎦⎢⎥⎢⎥--⎣⎦有n U C ==3rank满足能控性的充要条件，所以该系统能控。

3)由于该系统控制矩阵为110020B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=10030013A 则有，3101133030 00000012020AB ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 23103399030 0000012020A B ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦于是，系统的能控性矩阵为21133990000002220C U BABA B ---⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦可知n U C <=2rank不满足能控性的充要条件，所以该系统不完全能控。

(完整word版)《现代控制理论》第3版课后习题答案

(完整word版)《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

《现代控制理论》第3版课后习题答案.

《现代控制理论》第3版课后习题答案.

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

现代控制理论智慧树知到课后章节答案2023年下临沂大学

现代控制理论智慧树知到课后章节答案2023年下临沂大学

现代控制理论智慧树知到课后章节答案2023年下临沂大学临沂大学绪论单元测试1.现代控制理论的主要内容（）A:最优控制B:非线性系统理论C:线性系统D:系统辨识答案:最优控制;非线性系统理论;线性系统;系统辨识2.现代控制理论运用哪些数学工具（）A:微分方程B:线性代数C:几何学D:数理统计答案:微分方程;线性代数3.控制论是谁发表的（）A:奈奎斯特B:劳伦斯C:维纳D:钱学森答案:维纳4.大系统和与智能控制理论和方法有哪些（）A:鲁棒控制B:最优估计C:最优控制D:系统辨识答案:鲁棒控制;最优估计;最优控制;系统辨识5.下面哪个不是大系统的特点（）A:规模庞大B:信息复杂且多C:运用人力多D:结构复杂答案:运用人力多6.哪个不是20世纪三大科技（）A:进化论B:智能控制理论C:空间技术D:原子能技术答案:进化论7.经典控制理论形成的目的是采用各种自动调节装置来解决生产和军事中的简单控制问题。

（）A:错 B:对答案:对8.自适应控制所要解决的问题也是寻求最优控制律，自适应控制所依据的数学模型由于先验知识缺少，需要在系统运行过程中去提取有关模型的信息，使模型逐渐完善。

（）A:错 B:对答案:对9.非线性系统状态的运动规律和改变这些规律的可能性与实施方法，建立和揭示系统结构、参数、行为和性能之间的关系。

（）A:错 B:对答案:对10.现代控制理论是建立在状态空间法基础上的一种控制理论。

（）A:对 B:错答案:对第一章测试1.下面关于建模和模型说法正确的是（）A:无论是何种系统，其模型均可用来提示规律或者因果关系。

B:为设计控制器为目的建立只需要简练就可以了。

C:工程系统模型建模有两种途径，一是机理建模，而是系统辨识。

D:建模实际上是通过数据，图表，数学表达式，程序，逻辑关系或者各种方式的组合表示状态变量，输入变量，输出变量，参数之间的关系。

答案:无论是何种系统，其模型均可用来提示规律或者因果关系。

;工程系统模型建模有两种途径，一是机理建模，而是系统辨识。

《现代控制理论》课后习题全部答案(最打印版)

《现代控制理论》课后习题全部答案(最打印版)

第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••阿 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

《现代控制理论》习题解答 2016-5-18

《现代控制理论》习题解答 2016-5-18

2s 7 ( s 3)( s 4) 1-13 G ( s ) 1 s3
1 0 0 x 1 0 x 1-14 2 x 3 a2 0 4 a4 0 x y( z) 2( z 1) 2 1-15 u ( z ) ( z 3z 1)
10 s 26 ( s 2)( s 3)( s 4) 。 2s 10 ( s 2)( s 3)
0 x1 0 u1 y1 1 0 0 0 x2 ； 。 0 u2 y2 0 1 0 0 x3 b2 x4
x1 x2 x3 。 u ； (0 0 0 0 0 1) x4 x 5 x 6
1-04 设状态变量为 x1 i1 ， x2 i2 ， x3 uC ，状态方程， ： x1 i1 , x2 i2 , x3 uC ，状态方程
2( s 2) ( s 1)( s 3) 并联 G ( s ) W1 ( s ) W2 ( s ) 1 s 1
2( s 3) ( s 2)( s 4) 。 s 1 s2
第二章习题解答
1 0 0 A 2-01 (1) 注意 A 0 1 0 1 0 1 2 1 0 A1t 1 1 t ，其中 A1 1 ， A2 ，而 e L [( sI A1 ) ] e ， 1 2 A2
1 ( s 1)( s 3) 1-18 串联 G ( s ) W2 ( s )W1 ( s ) 1 ( s 1)2 s 2 5s 7 ( s 2)( s 3)( s 4) ； 1 ( s 1)( s 2)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1v(x) a 1x 12 b 1x 22 c 1 x 322x 1x 2 4x 3 x 2 2X 1X 3a 1 x T 11 b 1 2(1) v(x) x 12 4x 22 x 32 2x 1x 2 6x 3x 2 2x 1x 3 (2) v(x)x 12 10x 22 4x 32 6x 1 x 2 2x 3x 2222(3) v(x) 10x 14x 2 x 3 2x 1x 2 2x 3x 2 4x 1 x 3【解】：(1)二次型函数不定。

⑵二次型函数为负定。

⑶二次型函数正定。

3-4-2试确定下列二次型为正定时，待定常数的取值范围。

【解】：3-4-1第四章控制系统的稳定性试确定下列二次型是否正定。

1 1 11 11 1 114 3 ,1 0,3 0, 14 31 1 11 413 11 131P4100, 3 100,1010 P 12 1 , 10 1110 1 210 1 39 01411 42 1 10, 17a 1 0a 1b 1 1 a 1b 1c 1 4 b 1 4a 1 c 1【解】：(1)设2 2 v(x) 0.5x 10.5X 2V (X ) X 1X 1 X 2X 2 X 1X 2 X 1X 2 X2x/ °" °)为半负定。

0 (x 0)又因为v(x) 0时，有X 2 0, 则X 2 0，代入状态方程得： X 1 0. 所以系统在X 0时，v(x)不恒为零。

则系统渐近稳定，又因为是线性系统，所以该系统是大范围渐近稳定。

(2)设2 2v(x) 0.5X 1 0.5X 2v(x) X 1X 1 X 2X 2 X 1 ( X 1X 2) X 2(2X 1 3X 2)X 12 3X 22 3X 1X 2T 11.51 11 1.5Xx1 0,1.5 31 1 11.53T …X PxP 负定，系统渐近稳定，又因为是线性系统，所以该系统是大范围渐近稳定。

(3)0 1 1 1(1) XX(2) xX ； 1 1 2 31 11 0(3) xX (4) xX 1 10 13-4-3满足正定的条件为:a i | of 1 1b ia i 0, 1 11 1 b 12 02 C 1试用李亚普诺夫第二法判断下列线性系统的稳定性。

2 2v(x) 0.5x i 0.5x 2v(x) X i X t x 2x 2 X, X t x 2) x 2( X t x 2)x T PxP 负定，系统渐近稳定，又因为是线性系统，所以该系统是大范围渐近稳定。

(4)两个状态变量相互独立，所以可以单独分析各变量的稳定性。

3-4-4试确定下列系统平衡状态的稳定性。

1 3 0x(k 1)3 2 3 x(k)1【解】：方法一： 采用第一方法，确定特征多项式对应的特征值是否在单位圆内。

z i 3f(z) zI A 3 z 2 3i 0 zz i 0.ii73+2.6974i z 2 0.1173-2.6974i Z 31.2346特征多项式对应的特征值均在单位圆外，所以系统不稳定。

方法二： 采用第二方法，1 3 0 G 32 3。

12 2X i X 22X i X i v(X i ) 0.5x i2X 2 X 2 V (X 2)0.5X 2所以系统不稳定。

2 0 XV(X i )X i X i X i0 X 020 X 0 V (X 2) X 2X 2X 2X 01 0.5 0.5 P 0.51 0 0.51v(k) x T (k)(G T PG P)x( k)3 1 1 0.5 0.5 13 0 0.5 0 184.5 7 4.561.5 71.58v(k)为正定，所以系统在原点不稳定。

定时k 值范围。

【解】：方法采用第一方法，确定特征多项式对应的特征值是否在单位圆内。

z1 0f (z) zI A 0 z 10 0k/2z84.5 784.527.75 04.561.5 4.5 67 1.5 8因为8>0,4.5 0，所以P 正定。

10.5 0.51 0.50.75 00.51 0 0.510.510 ,所以P 正定。

v(x) x TPx 正定。

G T PG P 32 0 0.5 1 0 3-4-5因为1>0，0.5乙0.51 2kz2-0.5 2kZ3 00.5 2k 1 0 k 2时平衡点渐近稳定。

方法二：v(x) x T Px 正定。

v(k) x T(k)(G T PG P)x( k)v(k) x T (k)Qx(k)Q I1212 4 k2223R巳巳123RRR1231.^1.^1pp1ok-21111ppGpGP为正定，则124 k2120 k 2时系统渐近稳定。

3-4-6设系统的状态方程为X 10 1X 1，试求这个系统的李亚普诺夫函数， x 2 21.5 x 2然后再求从封闭曲线 v(x) 100边界上的一点到封闭曲线 v(x) 0.05内一点的响应时间上限。

【解】： 令Q IA T PPA I求矩阵P ，即2 P 1 P|2 P 11 P 12 0 1 1 0 11.5 P 21P 22P 21 P 2221.50 15.5所以李氏函数为:2 2v(x)(X 1 x 2 )1 1QP 1I P 1 I 03-4-7 试确定下列非线性系统在原点处的稳定性。

【解】：(1 )采用非线性系统线性化的方法，在平衡点原点处线性化得:I P 012.3062，20.6938t t 。

1ln V(X ，t) 1 , 0.05 In min V(X 0, t o )2 10010.955v(x)5.5 2X 1 42 0.5x 1x 2 0.5x 22s 22s 2系统的两个特征值均在右半平面，则系统在平衡点附近不稳定。

（2 ）采用非线性系统线性化的方法，在平衡点原点处线性化得:3-4-8试确定下列非线性系统在原点处稳定时的参数a 、b 的取值范围（其中二者均大于或等于零，但二者不同时为零）。

X 1 X 2 x 2x 1 ax 2 bx 23【解］:f 1 f 1Afx 0X 1 X 2 0 10 1 T Xf 2 f 21a 3bX 22x 01aX 1X 2x 01 1s 1 2siA 1 sas as 1结论：系统在原点渐近稳定的充要条件是 a 大于0, b 任意（同时还需满足题目要求）。

［解］:求平衡点：f 1 X 1 X 2 1 3X 12 11 1 T xxf 2 f 2113X 22 x 01 1X 1X 2x 011Asif 1f 1X 1 X 2 2 21 3x 1 x2 1 2x 1 x 2 f 2 f 22 21 2X 1X 21 X 1 3X2 x 0X 1X 2 x0s 1 As 1 1 1s 1s 2 2s 2 03-4-9试证明系统x 1 x 2x 2a 1x 1a 2x 12x 2在a 10,a ? 0时是全局渐近稳定的。

Ax系统的两个特征值都在左半平面，则系统在平衡点附近渐近稳定。

X i X 2x 2 0a i x i2 a 2X i X 2X ie0 0X 2e设v(x) 20.5a i X i20.5X 2v(x) a 1x 1 x 1 x 2x 2 a 1x 1x 2 x 2( a ^x 2 a 2x 12x 2)22v(x)a 2X i X2结论a i 0， v(x)正定；a 2 0， v(x)负定，系统渐近稳定。

因为时，v(x) 0.5a i X i 2 0.5X 22，所以系统又是大范围渐近稳定。

3-4-10 试用克拉索夫斯基法确定非线性系统在原点X e 0处为大范围渐近稳定时，参数a 和b 的取值范围。

[解]:v(x) f T (x)f(x)大范围渐近稳定的条件是:x 时 v(x)X Tf if i X i X 2 ai f 2 f 2 ii 3bx 22X i X 2v(x)f T (X)[J T J]f(x)2f T (x)i3bx 22 f(x)系统在x e0处渐近稳定的条件是v(x)负定。

而v(x)负定的条件为:a a 0,ii i 3bx 222a 3abx 2 i 0而 ||x | 时，v(x) (ax i X 2 )2 (x i X 2 bx 2 )2所以系统大范围渐近稳定的条件是：a 0,a i 2ii 3bX 2a 3abx 22 i 03-4-11试用变量-梯度法构成下述非线性系统的李氏函数。

x i x i 2x 1 x 2 x 2x 2【解】：求平衡点：X i X 22x 1 2x 1 x 2 x 20 X ieX 2e 0设Va ii X i a i2 X 2V ia 2i X i a 22X 2 V 2v(x)(V)T x2 a ii X i(a 12 a 21 )x 1x 22a 11x 13 x 2 2 2 22a 〔2 x 〔X 2 a 22 x 2若选a iia 221, a i2 V ia 21 0a 12V 22a 21 0X 2X i满足旋度方程条件v(x) xj(1 2X 1X 2) X 22。

当 x 1 x 20.5时，v(x)负定X i (X 2 0)X 2(x i X i )22 、 宀而 v(x)x i dx i x 2dx 2 0.5(x f x ；)为正定。

0 0当X i X 2 0.5时，系统在平衡点渐近稳定。

3-4-I2设非线性系统方程为试求系统原点X e 0稳定的充分条件。

【解】：由第一法，稳定条件为：由克拉索夫斯基法设f i f2 f2A f T X0XX i X i X2f3X2 X 0f i f20，f3X i X i X2v(X) T X X为正定。

TXv(x) Fxf lX i X i3-4-132(X iX2X1)f2X2X2X22上X2l iX if2X2f2X if3X2f i f2X i X if if2)X if3(-f2X i X2 X2f i f2X i X if i f2)X if3(-f2X i X2 X2时渐近稳定。

4(时稳定。

4()2)2试用阿依捷尔曼法分析下列非线性系统在原点X e 0处的稳定性。

结构如题3-4-13图所示。

(1)题3-4-13图【解】：当输入为零时，非线性系统方程可以写成e e F (e) 0若取状态变量：X 1 e, X 2 e ，那么系统的状态方程为:x 1 x 2 X 2 X 2 F (e)(1)在x e 0处将非，线性环节输入-输出特性用一直线近似 则线性化状态方程为：X 1 X 2⑵取二次型函数作为系统的李氏函数，则有(k 1)2时v(x)为负定，从而求得 0.382只要非线性环节的曲线在 0.382e 和2.618e 范围内变化，原非线性控制系统就是大范围渐近稳定的。