晶格振动模式密度

晶格振动模式密度定义晶格振动模式密度（Phonon Density of States，简称PDOS）是描述晶体中原子振动模式的一种物理量。

晶体中的原子在平衡位置附近以小振幅做简谐振动，这些简谐振动构成了晶体的振动模式。

PDOS给出了不同频率的振动模式在能量空间中的分布情况，反映了晶体各种振动模式的丰度和分布情况。

PDOS对于研究晶体的热力学性质、热传导、声学性质等都具有重要意义。

它是计算晶体热容、热导率、声子散射等性质的基础。

此外，PDOS还可以用于研究晶体的相变、物理化学性质以及材料的设计和优化。

PDOS的具体定义如下：设晶体中的原子总数为N，晶格振动模式的总数为M，则PDOS可以定义为每单位频率范围内单位原子数的平均数，即：PDOS(ω) = (1/ N) * ∑(m=1 to M) δ(ω - ω_m)其中，δ(ω-ω_m)为狄拉克函数，当ω等于ω_m时取值为1，否则取值为0。

PDOS可以分为各向同性的PDOS和各向异性的PDOS。

各向同性PDOS是指晶体中各个晶向上的振动模式在一些频率范围内的分布情况，它是晶体的各向同性介质的特征。

各向异性PDOS是指晶体中不同晶向上的振动模式在一些频率范围内的分布情况，它反映了晶体的各向异性效应，比如晶体的声子色散关系。

在实际计算中，PDOS通常通过量子力学计算或者分子动力学模拟得到。

对于固体材料，计算PDOS是一个复杂的过程，需要考虑晶胞、原子的排列方式、晶格常数等诸多因素。

目前，常用的计算方法包括密度泛函理论（DFT）、哈密顿动力学模拟（HMD）等。

根据计算得到的PDOS，可以进一步研究晶体的声子态密度（Phonon Density of States，简称PhDOS），PhDOS是PDOS的积分，表示在一些频率以下的所有振动模式的能量状态密度。

总结起来，晶格振动模式密度（PDOS）是指描述晶体中不同频率的振动模式在能量空间中的分布情况。

它是了解晶体物理、热学以及声学性质的重要指标，可以通过理论计算或者模拟得到。

晶格振动模式密度定义
晶格振动模式密度，也称为声子态密度，是固体物理学中一种描述晶格振动模式种类
和数量的物理量。

它指的是在特定材料中，固体内能够传播热量和声波的振动模式种类及
其频率密度分布的表征。

这个概念源于声子，它是一种量子力学的概念，解释了晶体内的振动。

当物质中的离
子或原子振动时，它们的能量以干扰的形式向其他周围原子传递，从而形成晶体中的声子。

声子态密度包括所有可能的振动模式类型的密度，每种振动模式代表一个特定的波数
和频率。

声子态密度与晶体中存在的原子的数量和种类有关，并在不同材料和不同温度下
变化。

它还与材料的结构和性质密切相关，因此是研究材料的热、电、磁性质等方面的重
要参量。

晶格振动模式密度可以用实验方法或理论计算方法得到，例如声子谱测量、密度泛函
理论等。

通过比较实验和理论结果，可以对材料的特性进行更深入的研究。

在材料科学研究中，声子态密度常常用于研究材料的热传导、声学性质、相变以及缺
陷和晶格畸变等方面，对于设计新型功能材料、优化材料性能具有重要意义。

03_09_晶格振动模式密度
晶体中的原子不是静态的，而是处于无限个振动模式之中。

这些振动模式以不同的频
率振动，并与晶格点的相互作用相互影响。

因此，晶体的振动模式密度是描述晶体振动行
为的一种重要工具。

晶格振动模式密度是指每单位频率内的振动模式数。

在固体物理学中，晶格振动模式
密度是描述晶体振动特性和热力学性质的重要物理量。

它反映了晶体中所有可能的振动模式，包括纵波和横波、彼此耦合的振动等。

晶格振动的频率区间通常被分为三个范围：远红外波段、中红外波段和近红外波段。

在每个频段中，振动模式密度随频率增加而增加，但在不同频率范围内的增长速度是不同的。

在远红外波段，晶格振动主要由晶体内部的振动和声波组成。

这些振动模式通常被称
为声子。

在中红外波段，晶格振动包括晶体的特定振动模式和局部原子的振动模式。

在近
红外波段，晶体中的振动模式包括晶体基元的整体振动和各原子之间的化学键振动。

晶格振动模式密度可以通过测量晶体的各种热力学性质来确定。

例如，温度和压力对
晶格振动模式密度的影响可以通过热容和热膨胀系数来测量。

这些测量结果可以揭示晶体
内在的能量状态和振动行为，从而为研究特定晶体中的物理和化学现象提供有价值的信息。

此外，晶格振动模式密度还可以用于开发新的材料和设计化学反应的方法。

总之，晶格振动模式密度是描述晶体内部振动行为以及热力学性质的重要物理量。

它
反映了晶体内部的能量状态和振动行为，可以在材料科学和化学领域中发挥重要作用，并
促进新颖材料和反应的开发。

一维简单晶格的格波模式密度-回复
一维简单晶格包含一列等间距的原子。

其格波模式密度可以通过计算在每个波矢k处的能量密度来得到，即
D(k)=\frac{1}{\pi}\sqrt{\frac{2E(k)}{\hbar\omega(k)}}
其中E(k)为能量，\omega(k)为频率，\hbar为普朗克常数。

对于一维简单晶格，格点振动只有一种类型，因此其能量和频率可以直接用单变量k表示：
E(k)=\frac{1}{2}M\omega^2a^2\sin^2\frac{ka}{2}
\omega(k)=\sqrt{\frac{4K}{M}}\sin\frac{ka}{2}
其中M为原子质量，K为弹性系数，a为晶格常数。

将上式代入可以得到格波模式密度的表达式：
D(k)=\frac{1}{\pi}\sqrt{\frac{2M\omega^2a^2\sin^2\frac{ka}{2}}{\hbar\s qrt{\frac{4K}{M}}\sin\frac{ka}{2}}}
化简后可得：
D(k)=\frac{1}{\pi}\sqrt{\frac{Ma}{2\pi\hbar K}}
因此，一维简单晶格的格波模式密度与晶格常数和弹性系数有关，与波矢k无关。

§3-6 晶格振动的模式密度3. 6. 1 晶格模式密度定义为了准确求出晶格热容以及它与温度的变化关系，必须用较精确的办法计算出晶格振动的模式密度（也叫频率分布函数）。

原则上讲，只要知道了晶格振动谱ωj (q )，也就知道了各个振动模的频率，模式密度函数g (ω)也就确定了。

但是，一般来说，ω与q 之间的关系是复杂的，除非在一些特殊的情况下，得不到g (ω)的解析表达式，因而往往要用数值计算。

图3-6-1给出了一个实际的晶体（钾）的模式密度，同时给出了德拜近似下的模式密度进行比较，可以看出除在低频极限以外，两个模式密度之间存在有一定的差别。

这可以说明为什么德拜热容理论只是在极低温下才是严格正确的。

因为在极低温下，只有那些低频振动模才对热容有贡献。

了解晶格振动模密度的意义不仅局限于晶格热容的量子理论。

实际上，计算所有热力学函数时都要涉及到对各个晶格振动模的求和，这就需要知道模式密度函数。

以后还会看到，在讨论晶体的某些电学性质、光学性质时，也要用到晶格振动模式密度函数。

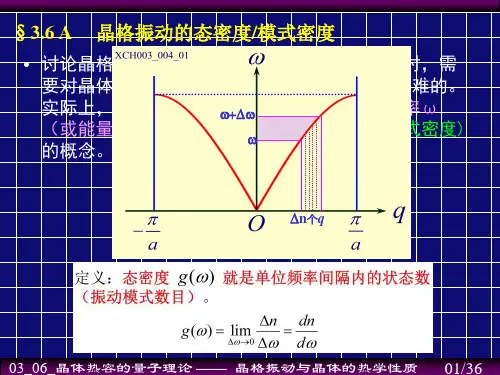
根据式（3-5-12），我们可以定义：()0limng ωωω∆→∆=∆…………………………………………………………（3-6-1）Δn 表示在ω—ω+Δω间隔内晶格振动模式的数目，如果在q 空间中，根据ω (q )=常数作出等频面，那么在等频面ω和ω+Δω之间的振动模式的数目就是Δn 。

由于晶格振动模（格波）在q 空间分布是均匀的，密度为V/3(2)π（V 为晶体体积），因此有：3((2)Vn ωωωπ∆=⨯∆频率为和+的等频率面间的体积)…………（3-6-2） 图3-6-1 钾的模式密度与德拜近似模式密度的比较如图3-6-2所示，等频面间的体积可表示成对体积元dsdq 在面上的积分：3(2)Vn dsdq π∆=⎰…………………………………………………（3-6-3） 其中dq 表示两等频率面间的垂直距离，ds 为面积元，显然()q dq q ωω∇=∆因为()q q ω∇表示沿法线方向频率的改变率。