3.2三维晶格振动 固体物理研究生课程讲义

《固体物理学》第二章晶格振动和固体比热第二章晶格振动和固体比热晶体中的格点表示原子的平衡位置，晶格振动便是指原子在格点附近的振动。

晶格振动对晶体的电学、光学、磁学、介电性质、结构相变和超导电性都有重要的作用。

本章的主题：用最近邻原子间简谐力模型来讨论晶格振动的本征频率；并用格波来描述晶体原子的集体运动；再用量子理论来表述格波相应的能量量子。

2-1、绝热近似和简谐近似绝热近似：考虑离子运动时，可以近似认为电子很快适应离子的位置变化。

为简单化，可以把离子的运动看成是近似成中性原子的运动。

简谐近似：r 设一维单原子晶体的布喇菲格子的格矢为R ，那么第n 个格点原子的位置r r r r矢量为：Rn na a 为基矢。

令第n 个原子相对其平衡位置Rn 的瞬时位置由与时r r r r间相关的矢量Sn 给出。

那么原子的瞬时位置为：rn Rn Sn 。

晶体的总势能应该为所有原子相互作用势能之和忽略均匀电子云产生的常1 r r势能项。

静态格点时的总势能：U 0 ∑ u0 Rn Rn ，u x 表示一维原子链中2 n n距离为x 的两原子的相互作用能。

1 r r 1 r r r r 考虑晶格振动时的总势能：U ∑ urn rn 2 ∑ u Rn Sn Rn Sn 2 n n nn 这时势能与动力学变量Sn有关，如果Sn是个小量，将势能U在平衡值U0附近1作泰勒展开：f r a f r a f r a 2 f r ...... 。

2 r r r r r r 取r Rn Rn a Sn Sn 1 r r 1 r r r r 1 r r r rU ∑ u0 Rn Rn 2 ∑ Sn Sn u0 Rn Rn 4 ∑ Sn Sn 2 u0 Rn Rn .... 2 n n nn nn 我们忽略高阶项，只保留二阶项第一项非零校正项，那么势能近似为：1 r r r r U U 0 ∑ S n S n 2 u0 Rn Rn 4 n n 上述近似称为简谐近似。

第四章 晶格振动和晶体的热学性质● 晶格振动：晶体中的原子在格点附近作热振动● 原子的振动以波的形式在晶体传播（原子的振动波称为格波） ● 晶格振动对晶体的性质有重要影响 主要内容● 晶格动力学（经典理论，1912年由波恩和卡门建立）晶格振动的模式数量（有多少种基本的波动解） 晶格振动的色散关系（波动的频率和波数的关系）● 晶格振动的量子理论 ● 固体的热容量 4.1 一维单原子链的振动原子链共有N 个原胞，每个原胞只有一个原子,每个原子具有相同的质量m,平衡时原子间距等于晶格常数a,原子沿链方向运动,第n 个原子离开平衡位置的位移用x n 表示,第n 个原子和第n+1个原子间的相对位移为 一维单原子链原子振动时，相邻两个原子之间的间距: 基本假设● 平衡时原子位于Bravais 格点上 ● 原子围绕平衡位置作微振动●简谐近似：原子间的相互作用势能只考虑到平方项 微振动时：简谐近似：势能展开式保留到二次项微振动：原子离开平衡位置的位移与原子间距相比是小量。

晶体中原子的平衡位置由原子结合能（势）决定。

任何一种晶体，原子间的相互作用势能可以表述成原子之间距离的函数。

n n x x -=+1δδ+=a x ()()⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=+=222 21 )(δδδa ax d U d x d U d a U a U x U把qa改变一个2π的整数倍，原子的振动相同，因此可以把qa限制负pi和正pi之间，此范围以外的q值，并不提供新的物理内容.群速度是指波包的传播速度，dw/dq,也就是能量在介质中的传播速度。

在布里渊区的边界上，群速度为零，波是一个驻波。

4.2 一维双原子链的振动q趋于0时，w也趋于零，称为声学波4.3 三维晶格的振动(略) 一个原胞中有n 个原子晶格基矢： 原胞数目： 原子的质量： 对于一个波矢q,有3n 个ω（即有3n 支色散曲线） 在3n 支色散关系中，当q→0时（长波）：有三支ω →0，且各原子的振幅趋于相同，这三支为声学波。

华中科技大学固体物理本次课的讲课内容第三章：晶格振动3.1简谐近似和简正坐标3.2一维单原子链3.3一维双原子链3.4三维晶格振动3.5确定晶格振动的试验方法3.1简谐近似和简正坐标晶格振动的研究最早从晶体的热学性质开始的，高温情况下热熔符合杜隆柏悌定则。

低温情况下，晶体热熔符合3T 律（涉及量子理论），研究晶体晶格振动的意义不限于热学性质，还包括晶体的电学性质，光学性质，超导电性，磁性，及结构相变，，，，从经典力学的观点看，晶格振动是典型的小震动问题，即，，，如果晶体包括N 个原子，平衡位置为n R ，偏离平衡位置的位移矢量为：()n t μ，则原子的实际位置矢量：()()'n n n R t t R μ=+，选用广义坐标系：位移矢量n μ用分量表示，N 个原子的位移矢量共有3N 个分量，写成：()1,2,......,3i i N μ=，以此作为广义坐标系，则整个原子体系的势能函数可以在平衡位置附近展开成泰勒级数：23301,1001......2NN i i j i i j i i jV V V V μμμμμμ==⎛⎫⎛⎫∂∂=+++∑∑⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭ 零表明是平衡位置时所具有的值。

可以设00V =,且有:00i V μ⎛⎫∂=⎪∂⎝⎭ 略去二阶以上的高阶项，就得到：23,1012N i j i j i jVV μμμμ=⎛⎫∂=∑⎪ ⎪∂∂⎝⎭,略去高阶项是有一定意义的，这称为简谐近似。

考虑到高阶项的作用，称为非简谐近似。

N 个原子体系的动能函数：203112N i i i T m μ==∑每个谐振子的波动方程的形式以及对应的能量本征值的形式，一定要记熟。

。

3.2一维单原子链晶体具有周期性，因而，晶格的振动模具有波的形式，称为格波。

将单原子链看做是一个最简单的晶格，平衡时相邻原子的距离为a ，每个原胞只含有一个原子，质量为m ，原子限制在沿链的方向移动，偏离格点的位移用：11......,,......n n n μμμ-+表示，只有相邻原子间存在相互作用，相互作用能可以一般写成：()()21 (2)a a νδνβδ+=++δ表示相对平衡位置a 的偏离。

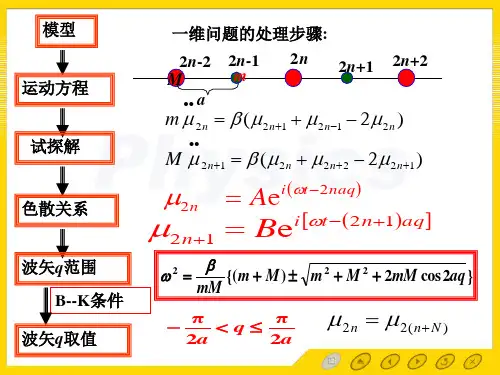
第三章 晶格振动与晶体热力学性质3-1 一维晶格的振动一、 一维单原子链(简单格子)的振动 1. 振动方程及其解(1)模型：一维无限长的单原子链，原子间距(晶格常量)为a ，原子质量为m 。

用xn 和xk 分别表示序号为n 和k 的原子在t 时刻偏离平衡位置的位移，用x nk = x n -x k 表示在t 时刻第n 个和第k 个原子的相对位移。

(2)振动方程和解平衡时，第k 个原子与第n 个原子相距0r a k n =-)(r u 为两个原子间的互作用势能，平衡时为)(0r u ，t 时刻为)()(0r r u r u δ+=)()(0r r u r u δ+=⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=3332220)(d d 61)(d d 21d d )(000r r u r r u r r u r u r r r δδδ ⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=3332220000d d 61d d 21d d )()(nk r nk r nk r x r u x r u x r u r u r u 第 n 个与第 k 个原子间的相互作用力:⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-=2332200d d 21d d d d nk r nk r nkx r u x r u r u f 振动很微弱时，势能展开式中忽略掉（δr ）二次方以上的高次项---简谐近似。

(忽略掉作用力中非线性项的近似---简谐近似。

) 得: nk nk r nkx x r u f β-=⎪⎪⎭⎫ ⎝⎛-=022d d 022d d r r u ⎪⎪⎭⎫⎝⎛=β()k n kn x x f --=∑β原子的振动方程: ()k n knx x mx--=∑β..只考虑最近邻原子间的相互作用，且恢复力系数相等：()()11..+-----=n n n n x x x x n m x ββ ()11..2+----=n n n x x x nm x β给出试探解：()naq t i n A x --=ωe ])1([1e aq n t i n A x +--+=ω原子都以同一频率ω，同一振幅A 振动,其中naq 表示第n 个原子在t=0时刻的振动相位，相邻原子间的位相差为aq 。