第四章量子力学模型

第四章 表象理论4.1 态的表象变换和态的矩阵表示1．态的表象变换将F 表象中的态函数对力学量算符ˆQ 在F 表象中的本征函数组展开，则展开系数就是在Q 表象中的态函数。

这就是将F 表象中的态函数变换到Q 表象中的态函数的方法。

为了便于求出展开系数，通常要求ˆQ的本征函数组为幺正基组。

以从r 表象变换到Q 表象为例。

r 表象中的态函数为(,)r t ϕ [或()r ϕ]。

设ˆQ的本征值为分立谱Q n ，对应的本征函数为()n r φ 。

当各Q n 都无简并时，(,)r t ϕ 对()n r φ的展开式为：(,)()()n n nr t a t r ϕφ=∑（4.1-1） 若Q n 表示几个对易力学量算符本征值的集合，则上式中的n 应表示几个对应的量子数的集合。

当Q n 存在简并时，展开式为：(,)()()iiin n n r t a t r ϕφ=∑（4.1-2）其中i 为描写简并的角标。

下面只讨论无简并的情况。

在（4.1-1）式中，a n (t)是Q n 与t 的函数，a n (t)相当于a(Q n ,t)的简写。

当Q n 在整个展开系数中变动。

由于Q n 为分立谱，所以函数关系a n (t)-Q n 不是连续的。

a n (t)就是(,)r t ϕ 变换到Ｑ表象中的态函数。

例如，将r表象中的某态函数(,,)r ϕθϕ对2ˆL 与ˆzL 的共同本征函数组(,)lm Y θφ展开： 0(,,)()(,)llm lm l m lr C r Y ϕθφθϕ∞==-=∑∑ （4.1-3）上式相当于（4.1-1）式中的n 表示两个量子数lm 的集合。

上式中的()lm C r 就是在2L 与z L 共同表象中的态函数。

2．本征态的排序本征态的排序可以化为对应的本征值的排序。

若本征值无简并，则参与排序的本征值没有相同者；若本征值有简并，则参与排序的本征值有相同者，其相同本征值的个数应与该本征值的简并度相同。

量子力学知识：量子理论模型的构建与演化量子力学是一门探究微观世界的物理学科，它的出现改变了我们对于物质世界的认识。

量子力学是基于一系列量子理论模型的构建与演化的。

这些模型主要由物理学家、数学家和哲学家共同构建，着重于描述量子力学中的基本元素和相互作用。

一、量子力学的基本框架量子力学的基本框架由两个部分组成，一是矩阵力学，另一个是波动力学。

矩阵力学是由德国物理学家海森堡于1925年提出的，波动力学则是由德国物理学家薛定谔于1926年提出的。

两种力学是等价的，在描述自然界的微观现象时都是有效的。

矩阵力学强调的是物理量的算符和对应的本征值，和它们之间的关系。

一种最常用的算符是哈密顿算符，它描述了一个系统的能量。

而本征值则代表着可能的物理状态，这些状态不同于我们在日常生活中观察到的宏观物理状态。

量子力学中的物理量是离散的，它们往往只能取有限个值。

这是显著不同于经典物理中连续物理量的描述。

与矩阵力学强调量子力学的算符不同，波动力学则更强调波函数的描述。

波函数是描述系统在各种状态下的可能性的函数。

它不仅可以描述一个粒子的位置，还可以描述其动量、自旋和其它的内在属性。

波函数的不同状态会产生不同的相位和幅度。

这些相位和幅度可以用来预测物理系统在不同情况下的概率分布。

这两种力学在很多方面都有相似之处，但其描述系统的角度和方法是不同的。

这两种方法为量子力学的发展提供了不同的视角，同时也为量子物理的应用提供了基础。

二、量子物理中的不确定性原理量子力学的一个基本原理就是不确定性原理。

这个原理说的是在量子力学中，无法同时精确测量一个粒子的位置和动量或者測量时间和能量这些之间的两个数值。

某个物理量的实际值和测量值的不确定性之间也有相互关联。

鉴于这个原理，人们不能够预测一个系统的状态或轨迹，而只能预测其态的概率分布。

不确定性原理的出现是量子力学最突出的成就之一。

它揭示了物理学中难以理解的现象。

它指出了永远不可能知道粒子的动量和位置，或者两个不共存的测量之间的复杂关系。

量子力学讲义第4章第四章量子力学的表述形式（本章对初学者来讲是难点）表象：量子力学中态和力学量的具体表示形式。

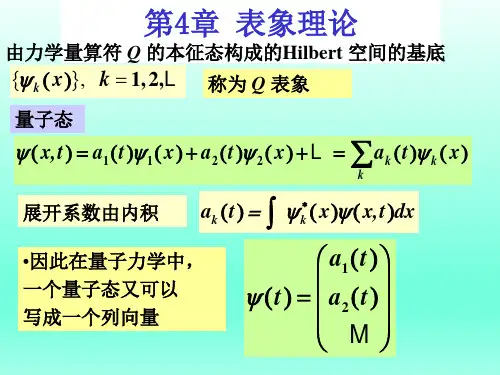
为了便于理解本章内容，我们先进行一下类比：矢量（欧几里德空间）量子力学的态（希尔伯特空间）基矢),,(321e e e~三维本征函数,...),...,,(21n ψψψ~无限维任意矢展开∑=ii i e A A任意态展开∑=nn n a ψψ),,(z y x e e e),...)(),...,(),((21x x x n ψψψ 取不同坐标系),,(?θe e e r取不同表象),...)(),...,(),((21p C p C p C n ………. ………. 不同坐标之间可以进行变换不同表象之间可以进行变换由此可见，可以类似于矢量A，将量子力学“几何化”→在矢量空间中建立它的一般形式。

为此，我们将① 引进量子力学的矢量空间~希尔伯特空间；② 给出态和力学量算符在该空间的表示；③ 建立各种不同表示之间的变换关系。

最后介绍一个典型应用（谐振子的粒子数表象）和量子力学的三种绘景。

4.1希尔伯特空间狄拉克符号狄拉克符号“”~类比：),,(z y x A A A欧氏空间的矢量 A→坐标系中的分量),,(?θA A A r……….)(rψ →表象下的表示)(p C……….引入狄拉克符号的优点：①运算简洁；②勿需采用具体表象讨论。

一、希尔伯特空间的矢量定义：希尔伯特空间是定义在复数域上的、完备的、线性内积空间，并且一般是无限维的。

1、线性：①c b a =+；②a b λ=。

2、完备性：∑=nn n a a 。

3、内积空间：引入与右矢空间相互共轭的左矢空间∑==?+nn n a a a a *;)(:。

定义内积：==*ab b a 复数，0≥a a 。

1=a a ~归一化；b a b a ,~0=正交；m n n m δ=~正交归一；)(x x x x '-='δ~连续谱的正交归一。

原子的量子力学模型引言：原子是构成物质的基本单位，其内部结构的研究对于理解物质的性质和相互作用至关重要。

量子力学模型是描述原子内部结构的一种理论框架，它基于量子力学的原理和方程，揭示了原子中电子的能级分布、轨道形状以及电子的运动规律。

本文将介绍原子的量子力学模型，探讨其基本原理和主要特征。

一、波粒二象性量子力学模型的基础是波粒二象性，即微观粒子既具有粒子的特征，又具有波动的特征。

在原子中，电子也具备波粒二象性，既可以看作是粒子，又可以看作是波动。

二、不确定性原理量子力学模型还依赖于不确定性原理，即海森堡不确定性原理和薛定谔不确定性原理。

海森堡不确定性原理表明，无法同时准确测量粒子的位置和动量，精确测量其中一个属性会导致另一个属性的不确定。

薛定谔不确定性原理则指出，无法同时准确测量粒子的能量和时间，精确测量其中一个属性会导致另一个属性的不确定。

三、薛定谔方程薛定谔方程是量子力学模型的核心方程，描述了原子中电子的运动规律。

薛定谔方程是一个波动方程，通过解方程可以得到电子的波函数，该波函数包含了电子的位置和能量信息。

四、能级和轨道量子力学模型提出了能级和轨道的概念，描述了电子在原子中的分布方式。

能级是电子的能量状态，每个能级对应一个特定的能量值。

轨道则是电子在原子中的运动路径，每个轨道有特定的形状和能量。

五、量子数量子力学模型引入了一系列量子数来描述电子的状态。

主量子数描述能级的大小，角量子数描述轨道的形状，磁量子数描述轨道在空间中的方向，自旋量子数描述电子的自旋方向。

六、波函数和概率密度波函数是量子力学模型中的核心概念，它描述了电子的波动性质。

波函数的平方值给出了电子出现在某个位置的概率密度，即电子在空间中的分布情况。

七、电子云模型电子云模型是量子力学模型中对电子分布的一种直观描述。

电子云表示电子在原子中的可能位置，云的密度越高，表示电子在该位置的概率越大。

八、能级跃迁和光谱原子的能级分布决定了原子的光谱特征。

高中化学必修一第四章教案【教学目的】1. 了解原子结构的基本组成和性质；2. 理解元素周期律的发展与规律；3. 掌握原子结构及元素周期律相关的概念和知识。

【教学重点】1. 原子结构的组成；2. 元素周期律的规律。

【教学难点】1. 原子结构的量子力学模型；2. 元素周期律的分类与规律。

【教学过程】一、导入（5分钟）引导学生思考：我们所熟知的物质是由什么组成的？在物质的最基本单位中，有什么特殊构造？这些构造又是如何排列的？二、原子结构的基本组成（30分钟）1. 原子的基本构造（10分钟）：介绍原子的基本组成，让学生了解原子核、质子、中子、电子的数量及运动轨道。

2. 原子的量子力学模型（10分钟）：讲解原子结构的量子力学模型，引导学生了解原子的能级和电子的排布规律。

3. 原子的物理性质（10分钟）：探讨原子结构对原子的性质影响，引导学生探索原子分子之间的相互作用。

三、元素周期律的发展与规律（30分钟）1. 元素周期律的历史（10分钟）：介绍元素周期律的历史发展，引导学生了解元素周期表的基本构造和分类。

2. 元素周期律的规律（10分钟）：解释元素周期律中元素的分类规律，引导学生理解元素周期表中各元素之间的关系。

3. 元素周期律的应用（10分钟）：探讨元素周期律在元素化学性质、元素周期表推断等方面的应用，引导学生理解元素周期律在化学研究中的重要性。

四、小结与拓展（10分钟）总结本节课重点内容，指导学生对原子结构及元素周期律进行综合梳理，拓展相关知识点。

【教学反思】本章教学难点主要在于量子力学模型和元素周期律的规律，需要通过举例、实验等方式引导学生深入理解。

同时，要培养学生的科学思维和实验能力，引导他们将所学知识应用到化学实践中。

第4章三维空间中的量子力学4.1 球坐标系中的薛定谔方程向三维情况的推广是直截了当的。

薛定鄂方程为：;i H t∂ψ=ψ∂ [4.1] 由经典能量可以得出哈密顿算符H 1V p p p mV mv z y x +++=+)(21212222 通过标准方法（现在应用于y ，z 以及x ）：,x p i x ∂→∂ ,y p i y∂→∂ ,z p i z ∂→∂ [4.2] 或者简洁地写为[4.3]这样[4.4]其中2222222zy x ∂∂+∂∂+∂∂≡∇ [4.5]是直角坐标系中的拉普拉斯算符。

势能V 和波函数ψ现在是(,,)x y z =r 和t 的函数。

在无穷小体元3d dxdydz =r 内发现粒子的几率为23(,)t d ψr r ，归一化条件是231,d ⎰ψ=r [4.6]其中积分是对整个空间进行。

如果势不显含时间，将有一组完备的定态/(,)(),n iE t n n t e ψ-ψ=r r [4.7]其中空间波函数n ψ满足定态薛定谔方程： [4.8]1当可能出现混淆时,我将在算符顶部放一个∧来区分它们与对应的经典力学量。

本章中不会有很多场合会出现这种混淆，用∧很麻烦，所以从现在起我不再用它。

（含时）薛定谔方程的一般解是/(,)(),n iE t n n t c e ψ-ψ=∑r r [4.9]其中常数n c 由初始波函数(,0)ψr 用通常的方法确定。

（假如势允许连续态，那么4.9式中的求和变为积分。

）*习题4.1（a ） 求出算符r 和p 的各分量之间的正则对易关系：[,]x y ，[,]y x p ，[,]x x p ，[,]y z p p 等等。

答案：[,][,]i j i j ij r p p r i δ=-= ，[,][,]0i j i j r r p p ==， [4.10]这里指标表示,,x y z , , , x y z r x r y r z ===。

（b ） 证明三维情况下的Ehrenfest 定理：1,d dt m =p 和 .d V dt=-∇p [4.11] (当然，上面每个式子表示三个方程—一个分量一个)。