东南大学统计信号处理实验实验三

《统计信号处理》实验一一、实验目的：1、掌握噪声中信号检测的方法；2、熟悉Matlab 的使用；3、掌握用计算机进行数据分析的方法。

二、实验内容：假设信号为()s t 波形如下图所示：在有信号到达时接收到的信号为()()()x t s t n t =+，在没有信号到达时接收到的信号为()()x t n t =。

其中()n t 是均值为零、方差为225n σ=（可自行调整）的高斯白噪声。

假设有信号到达的概率P(H 1)=0.6，没有信号到达的概率P(H 0)=0.4。

对接受到的信号分别在t = 0ms, 1ms, …, 301ms 上进行取样，得到观测序列()x n 。

1、利用似然比检测方法（最小错误概率准则），对信号是否到达进行检测；2、假设102C =，011C =。

利用基于Bayes 准则的检测方法，对信号是否到达进行检测；3、通过计算机产生的仿真数据，对两种方法的检测概率d P 、虚警概率f P 、漏警概率m P 和Bayes 风险进行仿真计算；4、通过改变P(H 1)和P(H 0)来改变判决的门限（风险系数10C 和01C 不变），观察检测方法的d P 、f P 、m P 和Bayes 风险的变化；5、改变噪声的方差，观察检测方法的d P 、f P 、m P 和Bayes 风险的变化；6、将信号取样间隔减小一倍(相应的取样点数增加一倍)，观察似然比检测方法的d P 、f P 、m P 和Bayes 风险的变化；7、根据()s t 设计一个离散匹配滤波器，并观察()x n 经过该滤波器以后的输出。

三、实验要求：1、设计仿真计算的Matlab 程序，给出软件清单；2、完成实验报告，对实验过程进行描述，并给出实验结果，对实验数据进行分析，给出结论。

四、设计过程：1、产生信号s(t)，n(t)，x(t)，t = 0ms, 1ms, …, 301ms ；其中：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧≤≤+-≤≤-≤≤+-≤≤-≤≤+-≤≤-≤≤+-≤≤=301290,30101289270,28101269230,5.12201229190,5.10201189140,6.625113990,6.42518930,2301290,301)(t t t t t t t t t t t t t t t t t s 2、根据定义似然比函数10(|)()(|)p x H x p x H Λ=，门限001()()P H P H Λ=，如果0)(Λ>Λx ，则判定1D ；否则，判定0D 。

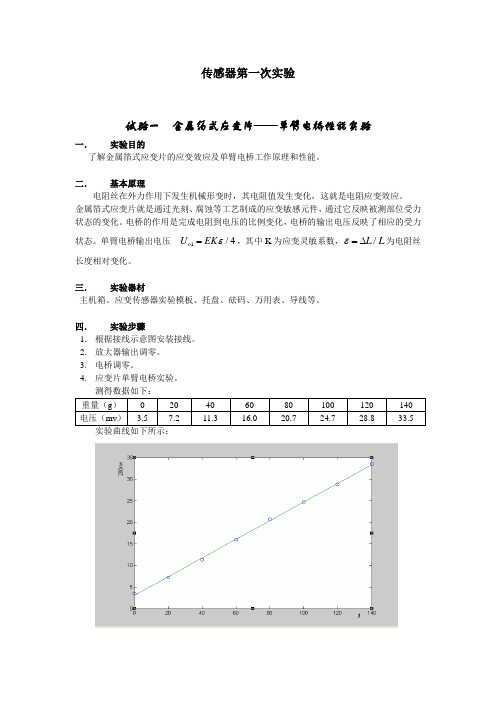
传感器第一次实验试验一 金属箔式应变片——单臂电桥性能实验一． 实验目的了解金属箔式应变片的应变效应及单臂电桥工作原理和性能。

二． 基本原理电阻丝在外力作用下发生机械形变时，其电阻值发生变化，这就是电阻应变效应。

金属箔式应变片就是通过光刻、腐蚀等工艺制成的应变敏感元件，通过它反映被测部位受力状态的变化。

电桥的作用是完成电阻到电压的比例变化，电桥的输出电压反映了相应的受力状态。

单臂电桥输出电压 1/4o U EK ε=，其中K 为应变灵敏系数，/L L ε=∆为电阻丝长度相对变化。

三． 实验器材主机箱、应变传感器实验模板、托盘、砝码、万用表、导线等。

四． 实验步骤1. 根据接线示意图安装接线。

2. 放大器输出调零。

3. 电桥调零。

4. 应变片单臂电桥实验。

测得数据如下： 重量（g ） 0 20 40 60 80 100 120 140 电压（mv ）3.57.211.316.020.724.728.833.5实验曲线如下所示：分析：由图可以看出，输出电压与加载的重量成线性关系，由于一开始调零不好，致使曲线没有经过原点，往上偏离了一段距离。

5. 根据表中数据计算系统的灵敏度/S U W =∆∆（U ∆为输出电压变化量，W ∆为重量变化量）和非线性误差/100%m yFS δ=∆⨯，式中m ∆为输出值（多次测量时为平均值）与拟合直线的最大偏差；yFS 为满量程输出平均值，此处为140g 。

U ∆=30mv ， W ∆=140g ， 所以 30/1400.2143/S mv g == m ∆=1.9768g ， yFS =140g ， 所以 1.9768/140100% 1.41%δ=⨯=6. 利用虚拟仪器进行测量。

测得数据如下表所示： 重量（g ） 0 20 40 60 80 100 120 140 电压（mv ）0.75.09.513.918.723.428.332.9相应的曲线如下：五． 思考题单臂电桥工作时，作为桥臂电阻的应变片应选用：（1）正（受拉）应变片；（2）负（受压）应变片；（3）正、负应变片均可以。

数字信号处理实验实验一信号、系统及系统响应1、实验目的认真复习采样理论、离散信号与系统、线性卷积、序列的z 变换及性质等有关内容；掌握离散时间序列的产生与基本运算，理解离散时间系统的时域特性与差分方程的求解方法，掌握离散信号的绘图方法；熟悉序列的z 变换及性质，理解理想采样前后信号频谱的变化。

2、实验内容a. 产生长度为500 的在[0,1]之间均匀分布的随机序列，产生长度为500 的均值为0 单位方差的高斯分布序列。

b. 线性时不变系统单位脉冲响应为h(n)=(0.9)nu(n)，当系统输入为x(n)=R10(n)时，求系统的零状态响应，并绘制波形图。

c. 描述系统的差分方程为：y(n)-y(n-1)+0.9y(n-2)=x(n)，其中x(n)为激励，y(n)为响应。

计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位脉冲响应h(n)；计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位阶跃响应s(n)；由h(n)表征的这个系统是稳定系统吗？d. 序列x(n)=(0.8)nu(n)，求DTFT[x(n)]，并画出它幅度、相位，实部、虚部的波形图。

观察它是否具有周期性？e. 线性时不变系统的差分方程为y(n)=0.7y(n-1)+x(n)，求系统的频率响应H(ejω)，如果系统输入为x(n)=cos(0.05πn)u(n)，求系统的稳态响应并绘图。

f. 设连续时间信号x(t)=e-1000|t|，计算并绘制它的傅立叶变换；如果用采样频率为每秒5000 样本对x(t)进行采样得到x1(n)，计算并绘制X1(ejω)，用x1(n)重建连续信号x(t)，并对结果进行讨论；如果用采样频率为每秒1000 样本对x(t)进行采样得到x2(n)，计算并绘制X2(ejω)，用x2(n)重建连续信号x(t)，并对结果进行讨论。

加深对采样定理的理解。

g. 设X1(z)=z+2+3z-1，X2(z)=2z2+4z+3+5z-1，用卷积方法计算X1(z)X2(z)。

练习三实验三五．1．>>help windowWINDOW Window function gateway.WINDOW(@WNAME,N) returns an N-point window of type specifiedby the function handle @WNAME in a column vector. @WNAME canbe any valid window function name, for example:@bartlett - Bartlett window.@barthannwin - Modified Bartlett-Hanning window.@blackman - Blackman window.@blackmanharris - Minimum 4-term Blackman-Harris window.@bohmanwin - Bohman window.@chebwin - Chebyshev window.@flattopwin - Flat Top window.@gausswin - Gaussian window.@hamming - Hamming window.@hann - Hann window.@kaiser - Kaiser window.@nuttallwin - Nuttall defined minimum 4-term Blackman-Harris window.@parzenwin - Parzen (de la Valle-Poussin) window.@rectwin - Rectangular window.@tukeywin - Tukey window.@triang - Triangular window.WINDOW(@WNAME,N,OPT) designs the window with the optional input argument specified in OPT. To see what the optional input arguments are, see the helpfor the individual windows, for example, KAISER or CHEBWIN.WINDOW launches the Window Design & Analysis Tool (WinTool).EXAMPLE:N = 65;w = window(@blackmanharris,N);w1 = window(@hamming,N);w2 = window(@gausswin,N,2.5);plot(1:N,[w,w1,w2]); axis([1 N 0 1]);legend('Blackman-Harris','Hamming','Gaussian');See also bartlett, barthannwin, blackman, blackmanharris, bohmanwin,chebwin, gausswin, hamming, hann, kaiser, nuttallwin, parzenwin,rectwin, triang, tukeywin, wintool.Overloaded functions or methods (ones with the same name in other directories) help fdesign/window.mReference page in Help browser doc window 2.>>N = 128;w = window(@rectwin,N); w1 = window(@bartlett,N); w2 = window(@hamming,N);plot(1:N,[w,w1,w2]); axis([1 N 0 1]); legend('矩形窗','Bartlett','Hamming');2040608010012000.10.20.30.40.50.60.70.80.913.>>wvtool(w,w1,w2)六．ts=0.01;N=20;t=0:ts:(N-1)*ts;x=2*sin(4*pi*t)+5*cos(6*pi*t);g=fft(x,N);y=abs(g)/100;figure(1):plot(0:2*pi/N:2*pi*(N-1)/N,y); grid;01234560.050.10.150.20.250.30.350.40.45ts=0.01; N=30;t=0:ts:(N-1)*ts;x=2*sin(4*pi*t)+5*cos(6*pi*t); g=fft(x,N); y=abs(g)/100;figure(2):plot(0:2*pi/N:2*pi*(N-1)/N,y); grid;012345670.10.20.30.40.50.60.7ts=0.01; N=50;t=0:ts:(N-1)*ts;x=2*sin(4*pi*t)+5*cos(6*pi*t); g=fft(x,N); y=abs(g)/100;figure(3):plot(0:2*pi/N:2*pi*(N-1)/N,y); grid;123456700.10.20.30.40.50.60.70.80.91ts=0.01; N=100;t=0:ts:(N-1)*ts;x=2*sin(4*pi*t)+5*cos(6*pi*t); g=fft(x,N); y=abs(g)/100;figure(4):plot(0:2*pi/N:2*pi*(N-1)/N,y); grid;012345670.511.522.5ts=0.01; N=150;t=0:ts:(N-1)*ts;x=2*sin(4*pi*t)+5*cos(6*pi*t); g=fft(x,N); y=abs(g)/100;figure(5):plot(0:2*pi/N:2*pi*(N-1)/N,y); grid;012345670.511.522.53实验八 1．%冲激响应 >> clear; b=[1,3]; a=[1,3,2]; sys=tf(b,a); impulse(sys); 结果：Impulse ResponseTime (sec)A m p l i t u d e%求零输入响应 >> A=[1,3;0,-2]; B=[1;2]; Q=A\B Q = 4-1>> clear B=[1,3]; A=[1,3,2];[a,b,c,d]=tf2ss(B,A) sys=ss(a,b,c,d); x0=[4;-1]; initial(sys,x0); grid; a =-3 -2 1 0 b =1 0 c =1 3 d = 001234560.20.40.60.811.21.4Response to Initial ConditionsTime (sec)A m p l i t u d e2.%冲激响应 >> clear; b=[1,3]; a=[1,2,2]; sys=tf(b,a); impulse(sys)Impulse ResponseTime (sec)A m p l i t u d e%求零输入响应 >> A=[1,3;1,-2]; B=[1;2]; Q=A\B Q =1.6000 -0.2000 >> clear B=[1,3]; A=[1,2,2];[a,b,c,d]=tf2ss(B,A) sys=ss(a,b,c,d); x0=[1.6;-0.2]; initial(sys,x0); grid; a =-2 -2 1 0 b = 10 c =1 3 d = 0Response to Initial ConditionsTime (sec)A m p l i t u d e3.%冲激响应 >> clear; b=[1,3]; a=[1,2,1]; sys=tf(b,a); impulse(sys)Impulse ResponseTime (sec)A m p l i t u d e%求零输入响应 >> A=[1,3;1,-1]; B=[1;2]; Q=A\B Q =1.7500 -0.2500>> clear B=[1,3]; A=[1,2,1];[a,b,c,d]=tf2ss(B,A) sys=ss(a,b,c,d); x0=[1.75;-0.25]; initial(sys,x0); grid; a =-2 -1 1 0 b =1 0 c =1 3 d = 00510150.20.40.60.811.21.41.6Response to Initial ConditionsTime (sec)A m p l i t u d e二． >> clear; b=1;a=[1,1,1,0]; sys=tf(b,a); subplot(2,1,1);impulse(sys);title('冲击响应'); subplot(2,1,2);step(sys);title('阶跃响应'); t=0:0.01:20; e=sin(t);r=lsim(sys,e,t); figure;subplot(2,1,1);plot(t,e);xlabel('Time');ylabel('A');title('激励信号'); subplot(2,1,2);plot(t,r);xlabel('Time');ylabel('A');title('响应信号');024681012141618200.511.5冲击响应Time (sec)A m p l i t u d e024681012141618205101520阶跃响应Time (sec)A m p l i t u d e02468101214161820-1-0.500.51Time A激励信号2468101214161820-10123TimeA响应信号三． 1.>> clear; b=[1,3]; a=[1,3,2]; t=0:0.08:8; e=[exp(-3*t)]; sys=tf(b,a); lsim(sys,e,t);0.10.20.30.40.50.60.70.80.91Linear Simulation ResultsTime (sec)A m p l i t u d e2.>> clear; b=[1,3]; a=[1,2,2]; t=0:0.08:8; sys=tf(b,a); step(sys)0.20.40.60.811.21.41.6Step ResponseTime (sec)A m p l i t u d e3．>> clear; b=[1,3]; a=[1,2,1]; t=0:0.08:8; e=[exp(-2*t)]; sys=tf(b,a); lsim(sys,e,t);0.10.20.30.40.50.60.70.80.91Linear Simulation ResultsTime (sec)A m p l i t u d eDoc: 1.>> clear; B=[1]; A=[1,1,1]; sys=tf(B,A,-1); n=0:200;e=5+cos(0.2*pi*n)+2*sin(0.7*pi*n); r=lsim(sys,e); stem(n,r);0204060801001201401601802002.>> clear;B=[1,1,1];A=[1,-0.5,-0.5];sys=tf(B,A,-1);e=[1,zeros(1,100)];n=0:100;r=lsim(sys,e);stem(n,r);010203040506070809010021 / 21。

一、实验目的本次实验旨在通过MATLAB软件平台，对数字信号处理的基本概念、原理和方法进行学习和实践。

通过实验，加深对以下内容的理解：1. 离散时间信号的基本概念和性质；2. 离散时间系统及其特性；3. 离散傅里叶变换（DFT）及其性质；4. 离散傅里叶逆变换（IDFT）及其应用；5. 窗函数及其在信号处理中的应用。

二、实验内容1. 离散时间信号的产生与性质（1）实验步骤：1.1 利用MATLAB生成以下离散时间信号：- 单位脉冲序列：δ[n]；- 单位阶跃序列：u[n]；- 矩形序列：R[n]；- 实指数序列：a^n；- 复指数序列：e^(jωn)。

1.2 分析并比较这些信号的性质，如自相关函数、功率谱密度等。

（2）实验结果：实验结果显示，不同类型的离散时间信号具有不同的性质。

例如，单位脉冲序列的自相关函数为δ[n]，功率谱密度为无穷大；单位阶跃序列的自相关函数为R[n]，功率谱密度为有限值；矩形序列的自相关函数为R[n]，功率谱密度为无穷大；实指数序列和复指数序列的自相关函数和功率谱密度均为有限值。

2. 离散时间系统及其特性（1）实验步骤：2.1 利用MATLAB构建以下离散时间系统：- 线性时不变系统：y[n] = x[n] a^n；- 非线性时不变系统：y[n] = x[n]^2；- 线性时变系统：y[n] = x[n] (1 + n)。

2.2 分析并比较这些系统的特性，如稳定性、因果性、线性时不变性等。

（2）实验结果：实验结果显示，不同类型的离散时间系统具有不同的特性。

例如，线性时不变系统的输出与输入之间存在线性关系，且满足时不变性；非线性时不变系统的输出与输入之间存在非线性关系，但满足时不变性；线性时变系统的输出与输入之间存在线性关系，但满足时变性。

3. 离散傅里叶变换（DFT）及其性质（1）实验步骤：3.1 利用MATLAB对以下离散时间信号进行DFT变换：- 单位脉冲序列：δ[n]；- 单位阶跃序列：u[n]；- 矩形序列：R[n]。

本次实验旨在通过实际操作加深对信号处理基本理论的理解，掌握信号频谱分析的方法，学习不同窗函数对信号频谱的影响，以及采样定理在信号处理中的应用。

通过实验，培养学生动手能力、分析问题和解决问题的能力。

二、实验原理1. 信号频谱分析：利用傅里叶变换将信号从时域转换为频域，分析信号的频率成分和能量分布。

2. 窗函数：在信号截取过程中，窗函数用于减少截取信号边缘的泄漏效应，提高频谱分析的准确性。

3. 采样定理：奈奎斯特采样定理指出，为了无失真地恢复原信号，采样频率应大于信号最高频率的两倍。

三、实验设备与软件1. 实验设备：示波器、信号发生器、计算机等。

2. 实验软件：MATLAB、Simulink等。

四、实验内容1. 信号频谱分析：（1）定义一个离散信号x[n]，计算其频谱X[k]。

（2）分别采用矩形窗、汉宁窗、汉明窗对信号进行截取，计算截取信号的频谱。

（3）比较不同窗函数对信号频谱的影响。

2. 采样定理验证：（1）根据奈奎斯特采样定理，确定信号的最大采样间隔和最小采样点数。

（2）通过改变采样点数，观察频谱变化，验证采样定理。

3. 周期性信号的DFT分析：（1）计算信号x[n]的周期T。

（2）通过补零和截取信号，分析周期性信号的DFT。

1. 在MATLAB中定义离散信号x[n]，并计算其频谱X[k]。

2. 分别采用矩形窗、汉宁窗、汉明窗对信号进行截取，计算截取信号的频谱。

3. 比较不同窗函数对信号频谱的影响。

4. 根据奈奎斯特采样定理，确定信号的最大采样间隔和最小采样点数。

5. 改变采样点数，观察频谱变化，验证采样定理。

6. 计算信号x[n]的周期T，通过补零和截取信号，分析周期性信号的DFT。

六、实验结果与分析1. 信号频谱分析：通过实验，发现不同窗函数对信号频谱的影响不同。

矩形窗频谱泄漏严重，汉宁窗和汉明窗能较好地抑制泄漏。

2. 采样定理验证：实验结果表明，当采样点数小于最小采样点数时，频谱发生严重混叠；当采样点数等于最小采样点数时，频谱能够无失真地恢复原信号。

统计信号处理实验三目的：掌握卡尔曼滤波滤波器的原理；内容：用雷达跟踪目标，目标的运动可以看成是在径向和横向内的二维运动，其运动方程和观测方程分别为：1111122222(1)()0100(1)()()0100(1)()0001(1)()()0001s k s k T v k v k u k s k s k T v k v k u k +⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦11112222(1)(1)(1)(1)1000(1)(1)(1)0010(1)s k y k v k w k y k s k w k v k +⎡⎤⎢⎥+++⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦⎢⎥+⎣⎦1()s k 、1()v k 和1()y k 分别为径向距离、速度和观测值，而2()s k 、2()v k 和2()y k 分别为横向距离、速度和观测值。

1()u k 和2()u k 是状态噪声，是目标速度的波动；1()w k 和2()w k 是观测噪声；四种噪声的均值都为0，呈高斯分布，互不相关。

T 是雷达扫描一次的时间，此处设为1.0秒。

假设目标距离雷达约160Km 左右，径向初速度设为300 m/s ，并且在向雷达靠近，横向初速度设为0 m/s 。

这样它的径向速度波动大，而横向速度波动小，所以我们假设1()u k 的方差21u σ为300m/s ，2()u k 的方差22u σ为11.210-⨯m/s 。

鉴于雷达的观测误差，我们假设观测噪声1()w k 和2()w k 的方差21w σ和22w σ均为1.0Km 。

其中21u σ，22u σ，21w σ和22w σ的初始值不是最佳的，学生完全可自己修改以上参数，并观察计算结果的变化，给出最好的滤波效果。

任务：1） 试用αβ-滤波法对信号进行处理，并通过计算机模拟对其跟踪过程进行验证；2） 试求其Kalman 滤波方程，并通过计算机模拟对其跟踪过程进行验证；3） 假设目标在运动过程中发生了机动（速度在某个时刻突然发生了改变），试观测此时的αβ-滤波和Kalman 滤波结果，并对结果进行解释。

《统计信号处理基础》实验指导书西北工业大学航海学院2006年 10 月实验一离散时间随机过程一、实验目的本实验的目的是在了解了Matlab编程语言的编程和调试的基础上，利用Matlab本身自带的函数来生成随机数，并根据随机数编程来计算随机过程的一些基本特征。

本实验主要是为了锻炼学生基本的Matlab编程，并利用信号处理工具箱的函数来完成基本的数据分析功能。

二、实验要求要求包括以下几个部分：1．要求独立完成实验的内容所要求的各项功能，编制完整的Matlab程序，并在程序中注释说明各段程序的功能。

2．要填写完整的实验报告，报告应包含程序、图形和结论。

要求记录在实验过程中碰到的问题，以及解决的方法和途径。

3．实验报告是现场用Word填写并打印完成。

个人或组必须在报告上署名。

三、实验环境实验所要求的设备：每组包含完整的计算机 1 台；可共用的打印机1台，A4纸张若干；计算机上安装的软件包括：Matlab 6.5以上（应包含Signal Processing Toolbox, Filter Design Toolbox）；Word 2000以上；四、实验内容、步骤实验内容包括2个，需要利用的Matlab函数包括fft, mean, var, randn, rand, xcorr, filter, plot, xlabel, ylabel, title等基本的函数。

实验1．本实验主要是分析高斯白噪声的样本自相关序列的估计精度。

a. 生成1000个零均值、单位方差的高斯白噪声，并用bar函数来画出直方图，与理想的高斯分布函数相比较；b. 采用xcorr函数的有偏估计来估计前100个自相关序列，用Plot函数画出该自相关序列，与理想的高斯白噪声的自相关序列相比。

c. 把这组数据分成互不重叠的10段，每段有100个样本。

分别对每段数据采用b中的方法来估计前100个样本自相关序列，然后对10段的自相关序列进行平均。

东南大学微机原理微机系统与接口实验三四实验报告范文自动化学院《微机实验及课程设计》实验报告学号08011东南大学《微机实验及课程设计》实验报告实验三TPC装置系统，I/O与存储器简单输入输出实验四（1）姓名：学号：08011专业：自动化实验室：计算机硬件技术实验时间：2022年04月9日报告时间：2022年04月21日评定成绩：审阅教师：《微机实验及课程设计》实验报告学号08011一.实验目的与内容实验三：(1)实验目的：1)2)3)4)了解掌握TPC实验系统的基本原理和组成结构，学会测试检查TPC-PCI总线转接卡地址；正确掌握I/O地址译码电路的工作原理，学会动态调试程序DEBUG/TD的直接I/O操作方法；学会利用I/O指令单步调试检查硬件接口功能，学会利用示波器检测I/O指令执行时总线情况；进一步熟悉8086/8088及PC机的分段存储特性，了解存储器扩展原理，完成编程及测试。

(2)实验内容：1)观察了解TPC-2003A实验系统的基本原理和组成结构，测试基本单元电路功能，熟悉各部分辅助电路的使用；2)通过Win/某P控制台硬件信息或测试程序检查TPC-PCI总线转接卡地址，并记录；3)按图3.3-5的I/O地址译码测试参考电路连线，分析电路原理，分别利用动态调试程序直接I/O操作功能和单步功能测试；4)编程利用片选负脉冲控制指示灯（如L7）闪烁发光（亮、灭、亮、灭、），时间间隔通过软件延时实现；5)修改延时参数，使亮(约1秒)与灭的时间间隔分别为1秒、5秒和8秒，记录延时程序对应参数B某,C某。

实验四：(1)实验目的6)进一步掌握TPC实验装置的基本原理和组成结构7)掌握利用I/O指令单步调试检查硬件接口功能，学会用示波器检测I/O指令执行时总线情况8)掌握简单并行输入输出接口的工作原理和使用方法，进一步熟悉掌握输入输出单元的功能和使用(2)实验内容9)连接简单并行输出接口电路，编程从键盘输入一个字符或数字，将其ASCII码通过这个输出接口电路输出，根据8个放光二极管发光情况验证正确性10)连接简单并行输入接口电路，用逻辑电平开关K0～K7预置一字母的ASCII码，编程输入这个ASCII码，并将其对应字母在屏幕上显示出来二.基本实验原理实验三：实验电路图见3.3-5，实验电路中D触发器CLK端输入脉冲时，上升沿使Q端锁存输出高电平L7发光，CD端为低电平时L7灭：《微机实验及课程设计》实验报告学号08011参考程序：程序名:decode.amioportequ0c800h-0280h;tpc卡中设备的IO地址outport1equioport+2a0h;CLK端译码输出端选为地址Y4outport2equioport+2a8h;CD端对应译码输出选为地址Y5tackegmenttackdb100dup()tackendcodeegmentaumec:code,:tackmainprocfartart:mova某,tackmov,a某movd某,outport1;Y4，置位，CLK端写outd某,alcalldelay;调延时子程序movd某,outport2;Y5，清空CD端写outd某,alcalldelay;调延时子程序movah,1int16hjetart;ZF=1，无键输入movah,4chint21h;返回DOS操作系统mainendpdelayprocnear;延时子程序movb某,2000ZZZ:movc某,0ZZ:loopZZdecb某2《微机实验及课程设计》实验报告学号08011jneZZZretdelayendpcodeendendtart实验四：(1)简单并行输入输出接口电路连线图输出接口电路输入接口电路(2)简单并行输入输出电路原理数据D0～D7先预存入273中，当输出端口2A8H和写信号同时低电平时，发生时钟触发，此时将数据运送到输出端Q1～Q8。

学生实验报告开课学院及实验室：电子楼317 2013 年 4 月 8 日N为周期进行周期延拓后的主值区序列，(一) 时域采样定理实验1. 给定模拟信号如下：0()sin()()at a x t Ae t u t -=Ω假设式中A=444.128,250π=a , 2500π=Ωrad/s ，将这些参数代入上式中，对()a x t 进行傅立叶变换，得到()a X j Ω，画出它的幅频特性()~a X jf f，如图3.1所示。

根据该曲线可以选择采样频率。

图3.1()a x t 的幅频特性曲线2. 按照选定的采样频率对模拟信号进行采样，得到时域离散信号()x n ：0()()sin()()anT a x n x nT Ae nT u nT ==Ω这里给定采样频率如下：1s f kHz =，300Hz ，200Hz 。

分别用这些采样频率形成时域离散信号，按顺序分别用1()x n 、2()x n 、3()x n 表示。

选择观测时间50p T ms=。

3. 计算()x n 的傅立叶变换()jwX e ：100()[()]sin()i i n anT jw j ni n X e FT x n Ae nT e ω--===Ω∑ （3.6）式中，1,2,3i =，分别对应三种采样频率的情况123111(,,)1000300200T s T s T s ===。

采样点数用下式计算：pi i T n T =（3.7）（3.6）式中，ω是连续变量。

为用计算机进行数值计算，改用下式计算：100()[()]sin()i k i k n jw anT jw n M i n X e DFT x n Ae nT e --===Ω∑ （3.8）式中，2k kM πω=，0,1,2,3...k =，1M -；64M =。

可以调用MATLAB 函数fft 计算3.8式。

4. 打印三种采样频率的幅度曲线()~k jw kX e w ，0,1,2,3...k =，1M -；64M =。

实验三光纤通信线路码实验一、实验目的1、了解光纤通信编译码方式2、了解各种编译码方式的性能3、了解光纤线路码的选码原则4、掌握CMI编码/译码原理二、实验内容1、学习光纤通信编译码方式2、了解各种码型的性能3、掌握光纤线路码的选码原则4、观察CMI编译码的波形5、学习CMI编译码模块的使用三、实验仪器示波器，RC-GT-II型光纤通信实验系统。

四、基本原理（一）、常见光纤线路码1．mBnB码mBnB码又叫分组码(BlockCode)。

其特点是将输入的原始简单二进制码流按m比特分组，形成m比特的码字，然后将每一码字在同样长的时隙内变成n比特的码字输出(取n>1m)。

常见的有1B2B码、3B4B码、4B6B码、5B6B码、5B7B码和6B8B码等等。

由于n>m，2n个nB码字中仅有2m个与mB码字对应，其余不用的nB码字称为禁字。

通常把nB码字中“1”、“0”个数悬殊的码字作为禁字，而且把录用的“1”、“0”个数不均字分成两种模式，并使“1”多的正模式与“0”多的负模式交替出现，这样就消除了线路码的直流电平浮动。

mB码字到nB码字的变换及逆变换是按预定的码表进行的，不同的码表产生不同的线路码性能。

mBnB码中，5B6B码被认为是在编码复杂性和比特冗余度之间最合理的折衷。

它的线路码速只比原始码速增加20％，而变换、反变换电路也不太复杂。

2．mBlP码mBIP码是一类脉冲插入码。

在原始mB码字后插入1比特P码，作为前面m比特码元的奇偶校验比特。

奇偶校验控制可以是奇数性的，也可以是偶数性的。

在偶数控制时，若mB中传号个数为偶数，取P码为“0”；若mB中传号个数为奇数，则取P码为“1”。

奇数性控制可以解决长连“0”问题，使连“0”数≤2m，当阴为奇数时又能使连“1”数≤2m。

偶数性控制不能解决连“0”问题，但便于不中断业务的误码监测。

应当指出，在某些外国产品资料中，线路码的名称不够规范，易造成mBlP码与mBnB的混淆，例如，7B8B码、17B18B码实际上是7B1P码和17B1P码(如图3-1所示)。

实验三多点信号平均器一、实验目的(1)了解多点信号平均器的原理(2)观察与测量多点信号平均器的输出特性二、基本原理多点信号平均器是一种信号处理装置，能从较强的干扰和噪声中提取信号，依据时域特性的取样平均来改善信噪比，复现被噪声掩没的信号波形。

它适用于重复信号的波形复现.在信号出现之后依次取多个信号样品，并按固定频率重复取样。

把每一个周期的许多取样信号，依次一一对应相加求平均，从而有效地改善了信噪比，对于多点信号平均器，可以由数字存储器或模拟存储器来实现求和平均，原理相同。

多点信号平均器的取样点的多少，与要求复现的波形精度有关。

取样点越多，复现波形越精确。

具体要采用多少点数，因根据要求复现的波形精度，成本及技术的可能性来决定。

目前采用数字存储器的多点信号平均器，通常选用1024个取样点。

采甩模拟存储器的多点信号平均器，通常选用120个取样点。

本实验是采用模拟存储器，优点是直观形象，便于理解，成本低廉，适于教学实脸。

这里只选用了8个取样点.虽然点数少了一些，但能更清楚直观地说明多点信号平均器的原理与特性。

模拟多点信号平均器的核心是门积分电路，门积分电路的单元电路如图3-1所示.它由电阻R，周期脉冲控制开关(场效应管或其它器件组成的)和积分电容C组成.图中，Vs为信号源，Vo为电容C两端的输出电压。

设控制开关的门脉冲的周期为TR门宽为Tg，引入单位幅度的门脉冲函教f (t)波形如图3-2所示.,21f(t),,，sin,,t ,oRn,1n,2,,,R,,T/TTgRR式中为相对门宽，为门脉冲的圆频率。

门积分电路的门接通时，R积分电阻为门断开时，积分电阻为?。

引入单位幅度的门脉冲函数后，积分电阻与开关Re能用等效积分电阻置换，这里RR,ef(t)o (3-2)于是,门积分电路便可用图3-3表示，形式上与普通积分电路相同。

只是电阻值是时间的函数。

积分电路的微分方程为:dVVVooi，,dtCR(t)CR(t)ee (3-3)VV,Viis式中，为积分器的输入电压，在图3 -3 中，。

第1篇一、实验目的1. 深入理解信号处理的基本原理和方法。

2. 掌握信号处理在各个领域的应用，如语音信号处理、图像处理等。

3. 熟悉实验设备的使用，提高实际操作能力。

4. 培养团队协作和问题解决能力。

二、实验内容本次实验主要分为以下几个部分：1. 语音信号处理（1）采集语音信号：使用麦克风采集一段语音信号，并将其转换为数字信号。

（2）频谱分析：对采集到的语音信号进行频谱分析，观察其频谱特性。

（3）噪声消除：设计并实现噪声消除算法，对含噪语音信号进行处理，提高信号质量。

（4）语音增强：设计并实现语音增强算法，提高语音信号的清晰度。

2. 图像处理（1）图像采集：使用摄像头采集一幅图像，并将其转换为数字图像。

（2）图像增强：对采集到的图像进行增强处理，如对比度增强、亮度增强等。

（3）图像滤波：设计并实现图像滤波算法，去除图像中的噪声。

（4）图像分割：设计并实现图像分割算法，将图像中的不同区域分离出来。

3. 信号处理算法实现（1）傅里叶变换：实现离散傅里叶变换（DFT）和快速傅里叶变换（FFT）算法，对信号进行频谱分析。

（2）小波变换：实现离散小波变换（DWT）算法，对信号进行时频分析。

（3）滤波器设计：设计并实现低通滤波器、高通滤波器、带通滤波器等，对信号进行滤波处理。

三、实验原理1. 语音信号处理（1）语音信号采集：通过麦克风将声音信号转换为电信号，再通过模数转换器（ADC）转换为数字信号。

（2）频谱分析：利用傅里叶变换将时域信号转换为频域信号，分析信号的频谱特性。

（3）噪声消除：采用噪声消除算法，如维纳滤波、谱减法等，去除信号中的噪声。

（4）语音增强：利用语音增强算法，如谱峰增强、长时能量增强等，提高语音信号的清晰度。

2. 图像处理（1）图像采集：通过摄像头将光信号转换为电信号，再通过模数转换器（ADC）转换为数字图像。

（2）图像增强：通过调整图像的亮度、对比度等参数，提高图像的可视效果。

（3）图像滤波：利用滤波器去除图像中的噪声，如均值滤波、中值滤波、高斯滤波等。

实验三：用FFT对信号作频谱分析实验报告一、实验目的与要求学习用FFT对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便正确应用FFT。

二、实验原理用FFT对信号作频分析是学习数字信号处理的重要内容，经常需要进行分析的信号是模拟信号的时域离散信号。

对信号进行谱分析的重要问题是频谱分辨率D和分析误差。

频谱分辨率直接和FFT的变换区间N有关，因为FFT能够实现的频率分辨率是2π/N，因此要求2π/N小于等于D。

可以根据此式选择FFT的变换区间N。

误差主要来自于用FFT作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当N较大时，离散谱的包络才能逼近连续谱，因此N要适当选择大一些。

三、实验步骤及内容（含结果分析）（1）对以下序列进行FFT分析：x 1(n)=R4(n)x2(n)=n+1 0≤n≤38-n 4≤n≤74-n 0≤n≤3n-3 4≤n≤7x(n)=3选择FFT的变换区间N为8和16两种情况进行频谱分析，分别打印出幅频特性曲线，并进行讨论、分析与比较。

【实验结果如下】：实验结果图形与理论分析相符。

（2）对以下周期序列进行谱分析：x(n)=cos[(π/4)*n]4(n)= cos[(π/4)*n]+ cos[(π/8)*n]x5选择FFT的变换区间N为8和16两种情况进行频谱分析，分别打印出幅频特性曲线，并进行讨论、分析与比较。

【实验结果如下】：（3）对模拟周期信号进行频谱分析：(n)= cos(8πt)+ cos(16πt)+ cos(20πt)x6选择采样频率Fs=64Hz，FFT的变换区间N为16、32、64三种情况进行频谱分析，分别打印出幅频特性曲线，并进行讨论、分析与比较。

【实验结果如下】：四、【附录】（实验中代码）x1n=[ones(1,4)]; %产生R4(n)序列向量X1k8=fft(x1n,8); %计算x1n的8点DFTX1k16=fft(x1n,16); %计算x1n的16点DFT%以下绘制幅频特性曲线N=8;f=2/N*(0:N-1);figure(1);subplot(1,2,1);stem(f,abs(X1k8),'.'); %绘制8点DFT的幅频特性图title('(1a) 8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度'); N=16;f=2/N*(0:N-1);subplot(1,2,2);stem(f,abs(X1k16),'.'); %绘制8点DFT的幅频特性图title('(1a) 16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度'); %x2n 和 x3nM=8;xa=1:(M/2); xb=(M/2):-1:1;x2n=[xa,xb]; %产生长度为8的三角波序列x2(n)x3n=[xb,xa];X2k8=fft(x2n,8);X2k16=fft(x2n,16);X3k8=fft(x3n,8);X3k16=fft(x3n,16);figure(2);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X2k8),'.'); %绘制8点DFT的幅频特性图title('(2a) 8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,3);stem(f,abs(X3k8),'.'); %绘制8点DFT的幅频特性图title('(3a) 8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度'); N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X2k16),'.'); %绘制8点DFT的幅频特性图title('(2a) 16点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');subplot(2,2,4);stem(f,abs(X3k16),'.'); %绘制8点DFT的幅频特性图title('(3a) 16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度'); %x4n 和 x5nN=8;n=0:N-1;x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n,8);X4k16=fft(x4n,16);X5k8=fft(x5n,8);X5k16=fft(x5n,16);figure(3);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X4k8),'.'); %绘制8点DFT的幅频特性图title('(4a) 8点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,3);stem(f,abs(X5k8),'.'); %绘制8点DFT的幅频特性图title('(5a) 8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度'); N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X4k16),'.'); %绘制8点DFT的幅频特性图title('(4a) 16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,4);stem(f,abs(X5k16),'.'); %绘制8点DFT的幅频特性图title('(5a) 16点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度'); %x8nFs=64; T=1/Fs;N=16;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k16=fft(x8n,16);N=16;f=2/N*(0:N-1);figure(4);title('(8a) 16点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度'); N=32;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k32=fft(x8n,32);N=32;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X8k32),'.'); %绘制8点DFT的幅频特性图title('(8a) 32点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度'); N=64;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k64=fft(x8n,64);N=64;f=2/N*(0:N-1);title('(8a) 64点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度');五、思考题及实验体会通过实验，我知道了用FFT对信号作频谱分析是学习数字信号处理的重要内容。

数电实验三东南大学电工电子实验中心实验报告课程名称：计算机逻辑结构及设计第三次实验实验名称：时序逻辑电路院（系）：吴健雄学院专业：姓名：学号：实验室: 实验组别：同组人员：实验时间：年月日评定成绩：审阅教师：一、实验目的1.2.3.4.5.6. 掌握时序逻辑电路的一般设计过程掌握时序逻辑电路的时延分析方法，了解时序电路对时钟信号相关参数的基本要求掌握时序逻辑电路的基本调试方法熟练使用示波器和逻辑分析仪观察波形图掌握ISE软件的使用方法掌握VHDL语言二、实验原理数字电路根据逻辑功能的不同特点，可以分成两大类，一类叫组合逻辑电路（简称组合电路），另一类叫做时序逻辑电路（简称时序电路）。

组合逻辑电路在逻辑功能上的特点是任意时刻的输出仅仅取决于该时刻的输入，与电路原来的状态无关。

而时序逻辑电路在逻辑功能上的特点是任意时刻的输出不仅取决于当时的输入信号，而且还取决于电路原来的状态，或者说，还与以前的输入有关。

常用时序逻辑器件：1. D触发器D触发器有六个端口，CP接时钟周期信号，D为信号输入端。

Q 和~Q为信号输出端，~S和~R为使能控制端。

在两个使能控制端都输入1时触发器锁存D，~R为0，~S为1时输出Q为1，反之输出Q 为0.不允许两个使能端同时为0，会造成不稳定的未知状态。

D触发器是时序逻辑电路的基本器件，主要作用是在时钟信号上升沿将D的信号输出。

2. MSI计数器计数器74161为模16计数器，其中包含两个使能端ENP和ENT，一个同步置数端~L,置数输入端D0~3，异步清零端~CLR，输出端Q0~3以及进位信号CO。

计数器在时钟的上升沿输出加1.除了74161外，还有74160、74163、74193、74197、74192等等，不同的MSI计数器有不同的特殊功能，但本质都类似，只是遵循不同的码制，清零置数方式以及增减模式而已。

计数器常用来制作分频器。

3. 移位寄存器移位寄存器74194包括工作模式控制端S1S0，置数输入端D0~3，输出端Q0~3以及串行输入端。

实验三简单编程练习姓名：学号：1.在一个数据块中找出最大数。

假设有数据22、46、32、72、84、16，且为不带符号的正整数，数据块的长度放在CX寄存器中，找出的最大数存放在以MAXN为符号的单元中。

程序：DATA SEGMENTNUM DB 22, 46, 32, 72, 84, 16MAXN DB ?DATA ENDSMAIN SEGMENTASSUME CS: MAIN, DS: DATASTART:MOV AX, DATAMOV DS, AX;将DATA地址传送到DS中MOV CX, 5;将长度5传送到CX中MOV AL, 00;将AL置0LEA BX, NUM;将NUM的偏移地址传送到BX中AGAIN:MOV AL, [BX]CMP AL, [BX+1]JNBE NEXTMOV AL, [SI+1]MOV MAXN, AL;将NUM中的数进行比较，并将较大的数传送到MAXN中NEXT:INC BXMOV MAXN, ALLOOP AGAIN;重复进行AGAIN选出最大数MAIN ENDSEND START结果：[DS:0006]=54H2.求无符号字节数据之和，和数为8位二进制数。

假设有数据38、55、26、12、23，数据块的长度存放在CX寄存器中，和数存放在以SUM为符号的单元中。

程序：DATA SEGMENTNUM DB 38, 55, 26, 12, 23SUM DB ?DATA ENDSMAIN SEGMENTASSUME CS: MAIN, DS: DATASTART: MOV AX, DATAMOV DS, AX;将DATA地址传送到DS中SUB AX, AX;将AX置零MOV CX, 4;将数据块长度传送到CX中MOV AL, [BX]LEA BX, NUM;将NUM的偏移地址传送到BX中AGAIN: MOV AH, [BX+1]ADC AL, AHINC BXLOOP AGAINMOV SUM, AL;将数据块中的数据进行相加，并将得到结果传送到SUM中MAIN ENDSEND START结果：[DS:0005]=9AH3. 求无符号字节数据之和，和数为16位二进制数。

《统计信号处理》实验二 实验目的：1．掌握参数估计方法；2．掌握用计算机分析数据的方法。

实验内容：假设一个运动目标，在外力作用下作一维匀加速运动。

其运动轨迹满足的方程为：0221)(s vt at t s ++=。

其中a 为目标的加速度，v 为t=0时目标运动的速度（初速度），0s 为目标在t=0时的初始位置。

对目标位置的观测结果为：()()()x t s t n t =+ 其中()x t 为观测到的目标位置，()(0,1)n t N ∈，为白色观测噪声。

假设在t=0,1,2,…,99s 时刻分别取得了100个观测结果x(0),x(1),…,x(99)。

1） 分别用最大似然，最小二乘方法，根据观测结果求出a ，v 和0s ；2） 用Monte_Carlo 法，计算出上面两种方法求出的参数的偏差和方差；3）利用估计出的参数，得到目标位置的时间参数()s t 的估计()st ，并用Monte_Carlo 法计算在t=0,1,2,…,99s 等各个时间点上对目标位置估计的方差和偏差；4） 将噪声的分布改为在（-1，+1）区间分布，应用上面推导出的最大似然，最小二乘公式对参数进行估计，并计算估计的偏差和方差。

实验要求：1)设计仿真计算的Matlab 程序，给出软件清单；2)完成实验报告，对实验结果进行描述，并给出实验结果，对实验数据进行分析。

实验结果如下：最小二乘法：010********607080901000102030405060708090time(t)s (t )&x (t )The least square method——a=0.0098;v=0.35;s0=3.2;delta=1-----------------------------最大似然估计方法----------------------010********607080901000102030405060708090time(t)s (t )&x (t )The most likelihood method——a=0.0098;v=0.35;s0=3.2;delta=1实验结果分析：可以发现对于估测结果a最好，估测结果v次之，估测结果s0最差。