1第一章语音信号处理实验解析
- 格式:ppt
- 大小:2.34 MB
- 文档页数:65
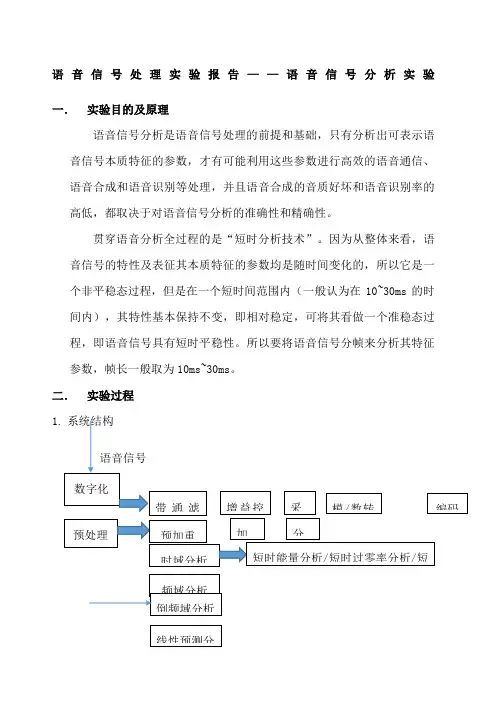

通信工程学院12级1班罗恒2012101032实验一语音信号的低通滤波和短时分析综合实验一、实验要求1、根据已有语音信号,设计一个低通滤波器,带宽为采样频率的四分之一,求输出信号;2、辨别原始语音信号与滤波器输出信号有何区别,说明原因;3、改变滤波器带宽,重复滤波实验,辨别语音信号的变化,说明原因;4、利用矩形窗和汉明窗对语音信号进行短时傅立叶分析,绘制语谱图并估计基音周期,分析两种窗函数对基音估计的影响;5、改变窗口长度,重复上一步,说明窗口长度对基音估计的影响。
二、实验目的1.在理论学习的基础上,进一步地理解和掌握语音信号低通滤波的意义,低通滤波分析的基本方法。
2.进一步理解和掌握语音信号不同的窗函数傅里叶变化对基音估计的影响。
三、实验设备1.PC机;2。
MATLAB软件环境;四、实验内容1。
上机前用Matlab语言完成程序编写工作.2。
程序应具有加窗(分帧)、绘制曲线等功能。
3.上机实验时先调试程序,通过后进行信号处理。
4.对录入的语音数据进行处理,并显示运行结果。
5。
改变滤波带宽,辨别与原始信号的区别。
6。
依据曲线对该语音段进行所需要的分析,并且作出结论。
7.改变窗的宽度(帧长),重复上面的分析内容。
五、实验原理及方法利用双线性变换设计IIR滤波器(巴特沃斯数字低通滤波器的设计),首先要设计出满足指标要求的模拟滤波器的传递函数Ha(s),然后由Ha(s)通过双线性变换可得所要设计的IIR滤波器的系统函数H(z)。
如果给定的指标为数字滤波器的指标,则首先要转换成模拟滤波器的技术指标,这里主要是边界频率Wp和Ws的转换,对ap和as指标不作变化。
边界频率的转换关系为∩=2/T tan(w/2).接着,按照模拟低通滤波器的技术指标根据相应设计公式求出滤波器的阶数N和3dB截止频率∩c ;根据阶数N查巴特沃斯归一化低通滤波器参数表,得到归一化传输函数Ha(p);最后,将p=s/ ∩c 代入Ha(p)去归一,得到实际的模拟滤波器传输函数Ha(s)。
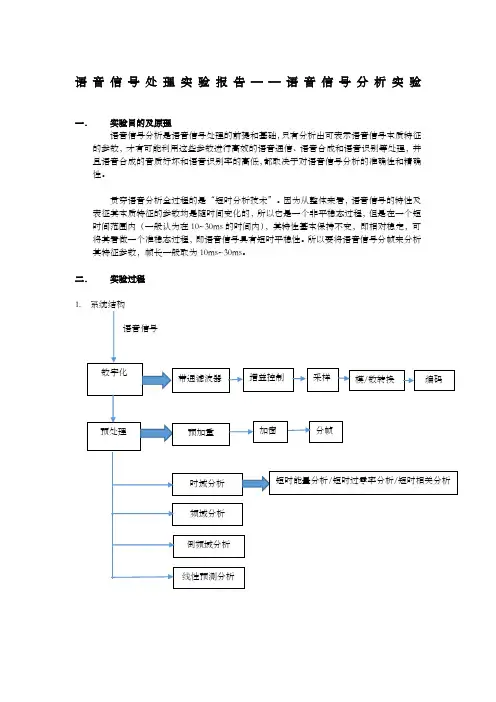
语音信号处理实验报告——语音信号分析实验一.实验目的及原理语音信号分析是语音信号处理的前提和基础,只有分析出可表示语音信号本质特征的参数,才有可能利用这些参数进行高效的语音通信、语音合成和语音识别等处理,并且语音合成的音质好坏和语音识别率的高低,都取决于对语音信号分析的准确性和精确性。
贯穿语音分析全过程的是“短时分析技术”。
因为从整体来看,语音信号的特性及表征其本质特征的参数均是随时间变化的,所以它是一个非平稳态过程,但是在一个短时间范围内(一般认为在10~30ms的时间内),其特性基本保持不变,即相对稳定,可将其看做一个准稳态过程,即语音信号具有短时平稳性。
所以要将语音信号分帧来分析其特征参数,帧长一般取为10ms~30ms。
二.实验过程1.2. 仿真结果(1) 时域分析男声及女声(蓝色为时域信号,红色为每一帧的能量,绿色为每一帧的过零率)x 104-0.6-0.4-0.200.20.40.60.81x 105-0.4-0.200.20.40.60.811.2某一帧的自相关函数-1-0.8-0.6-0.4-0.200.20.40.60.813. 频域分析①一帧信号的倒谱分析和FFT 及LPC 分析对应的倒谱系数:119.2,-7.6895,……对应的LPC 预测系数:1,-0.1,-0.02,-0.4,-0.27,……②男声和女声的倒谱分析③浊音和清音的倒谱分析原语音波形一帧语音波形一帧语音的倒谱④浊音和清音的FFT分析和LPC分析(红色为FFT图像,绿色为LPC图像)三.实验结果分析1.时域分析实验中采用的是汉明窗,窗的长度对能否由短时能量反应语音信号的变化起着决定性影响。
这里窗长合适,En能够反应语音信号幅度变化。
同时,从图像可以看出,En可以作为区分浊音和清音的特征参数。
短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。
从图中可以看出,短时能量和过零率可以近似为互补的情况,短时能量大的地方过零率小,短时能量小的地方过零率较大。


语音信号信号处理实验报告实验一语音信号的端点检测一、实验目的1、掌握短时能量的求解方法2、掌握短时平均过零率的求解方法3、掌握利用短时平均过零率和短时能量等特征,对输入的语音信号进行端点检测。
二、仪器设备 HP计算机、Matlab软件三、实验原理 3.1、短时能量3.1.1、原理:语音信号能量随时间有相当大的变化,特别是清音段的能量一般比浊音段的小得多。
语音信号的短时能量定义:xw(n)?w(n)?x(n)0?m?N?10?n?N?1?1w(n)?? 其它?0n?N?1 2En??xw(m) m?n3.1.2、短时能量序列反映了语音振幅或能量随着时间缓慢变化的规律。
从原始语音信号图中可以看到语音信号幅度随时间有相当大的变化,特别是清音段的幅度一般比浊音段的幅度小很多,语音信号的短时能量给出了反映这些幅度变化的一个合适的描述方法。
3.1.3、短时平均幅度函数和能量函数的作用 (1)区分清/浊音。
En、Mn大,对应浊音; En、Mn小,对应清音。
其中Mn是短时幅度差。
(2)在信噪比高的情况下,能进行有声/无声判决。
无声时,背景噪声的En、Mn小;有声时,En、Mn显著增大。
判决时可设置一个门限。
(3)大致能定出浊音变为清音的时刻,或反之。
3.2、短时过零率:3.2.1、定义:过零就是信号通过零值。
连续语音信号,考察其时域波形通过时间轴的情况;离散时间信号,相邻的值改变符号则称为过零。
n?N?11 Z?sgn[xw(m)]?sgn[xw(m?1)] n2m?n x(n)?0?1sgn[x(n)]????1x(n)?0窄带信号,平均过零数作为信号频率的一种简单度量是很精确的,语音信号序列是宽带信号,则不能简单用上面的公式,但是可以用短时平均过零数来得到频谱的粗略估计。
3.2.2、短时过零分析的意义:(1)、可以区分清音与浊音:浊音时具有较低的平均过零数,而清音时具有较高的平均过零数。
(2)、利用它可以从背景噪声中找出语音信号,可用于判断寂静无语音和有语音的起点和终点位置。

语⾳信号处理第⼀章绪论第⼀章绪论1、语⾳信号?语⾳信号是具有声⾳的语⾔,⼈类表⽰信息的常⽤媒体,⼈类通信的有效⼯具。
2、语⾳信号包含的信息?1)说话内容,说什么;2)说话⼈⾝份,谁说的;3)说话⼈说话时的状态,⽣理状态、⼼理状态、情绪等。
(语⾳信号处理主要关⼼前两项)3、为什么要学习和研究语⾳信号处理技术?答:1)语⾳是⼈类最重要、最有效、最常⽤和最⽅便的交换信息的⽅式;2)让计算机能够理解⼈类的语⾔,是⼈类⾃计算机诞⽣以来就梦寐以求的想法;随着计算机的便携化,⼈们渴望摆脱键盘的束缚⽽代之以语⾳输⼊的⽅式。
⽐如苹果公司的iphone⼿机,在其最新版本4s中,推出了siri功能-即语⾳助⼿,可以通过语⾳输⼊,让其充当闹钟,⽐如还可以让它为你找出最近的咖啡厅,另外找出⾏路线往往需要输⼊不少⽂字,省事的话,报出地点,它可以调⽤google地图来找出出⾏⽅案,还可以让它播放⾳乐,发送短信等等。
3)语⾳信号技术始终与当时信息科学最活跃的前沿科学保持密切联系,并且⼀起发展。
语⾳信号处理是以语⾳语⾔学和数字信号处理为基础的涉及多⽅⾯的综合性学科,它与⼼理学、⽣理学、计算机科学、通信与信息科学以及模式识别和⼈⼯智能等学科都有着密切的关系。
对于语⾳信号处理的研究⼀直是数字信号处理技术发展的重要推进⼒量,⽽数字信号处理许多新⽅法的提出,⼜是⾸先在语⾳信号处理中获得成功,⽽后再推⼴到其他领域的。
⽐如,语⾳信号处理算法的复杂性和实时处理的要求,促进了⾼速信号处理器的设计。
⽽这些产品产⽣之后,⼜是⾸先在语⾳信号处理中得到最有效的应⽤的。
4、语⾳信号处理的发展情况1)语⾳信号处理的发展标志是在1940年产⽣的通道声码器技术,该技术打破了以往的“波形原则”,提出了⼀种全新的语⾳通信技术,即从语⾳中提取参数加以传输,在接收端重新合成语⾳。
其后,产⽣了“语⾳参数模型“的思想。
2)40年代后期,研制成功了“语谱仪”,为语⾳信号分析提供了有⼒的⼯具。

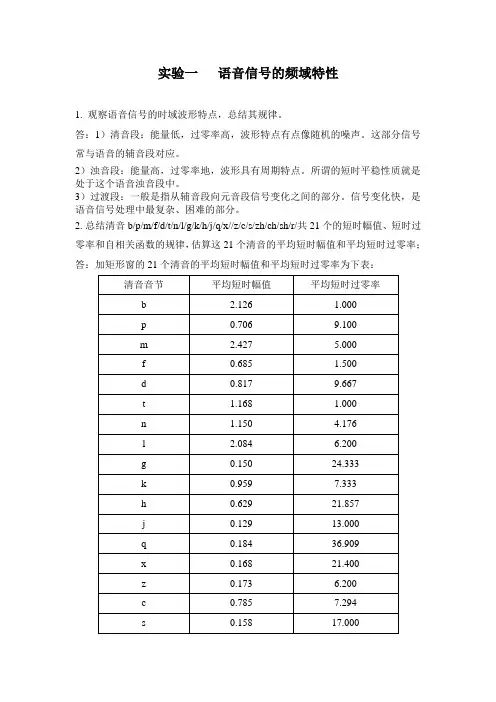
实验一语音信号的频域特性1. 观察语音信号的时域波形特点,总结其规律。
答:1)清音段:能量低,过零率高,波形特点有点像随机的噪声。
这部分信号常与语音的辅音段对应。
2)浊音段:能量高,过零率地,波形具有周期特点。
所谓的短时平稳性质就是处于这个语音浊音段中。
3)过渡段:一般是指从辅音段向元音段信号变化之间的部分。
信号变化快,是语音信号处理中最复杂、困难的部分。
2.总结清音b/p/m/f/d/t/n/l/g/k/h/j/q/x//z/c/s/zh/ch/sh/r/共21个的短时幅值、短时过零率和自相关函数的规律,估算这21个清音的平均短时幅值和平均短时过零率;答:加矩形窗的21个清音的平均短时幅值和平均短时过零率为下表:清音音节平均短时幅值平均短时过零率b 2.126 1.000p 0.706 9.100m 2.427 5.000f 0.685 1.500d 0.817 9.667t 1.168 1.000n 1.150 4.176l 2.084 6.200g 0.150 24.333k 0.959 7.333h 0.629 21.857j 0.129 13.000q 0.184 36.909x 0.168 21.400z 0.173 6.200c 0.785 7.294s 0.158 17.000zh 0.203 31.500ch 0.237 27.535sh 0.182 28.692r 1.814 5.5333. 总结浊音a/o/e/i/u/v/ao/ai/ei/ou/an/en/in/ang/eng/ong/ing/共17个的短时幅值、短时过零率和自相关函数的规律,估算这17个浊音的平均短时幅值和平均短时过零率,从自相关函数上估算这17个浊音的基音周期;答:浊音能量高,短时幅值也比较高,短时过零率比较低,由于浊音有一定的准周期性,所以自相关函数有比较明显的峰值和周期性。
浊音音节平均短时幅值平均短时过零率基音周期a 3.662 0.643 57o 2.948 0.184 71e 2.531 0.148 59i 1.693 0.061 60u 1.300 0.032 61v 1.081 0.024 66ao 2.000 0.123 71ai 2.307 0.121 57ei 1.828 0.074 67ou 0.294 0.000 67an 1.500 0.061 58en 1.827 0.073 54in 2.257 0.118 56ang 0.591 0.009 65eng 1.473 0.053 56ong 1.712 0.059 64ing 0.494 0.014 714. /r/、/m/、/n/ 从这几个音素的自相关函数图形判断为“清音”还是“浊音”,若为浊音估算其基音周期;答:(1)/r/: 自相关函数具有周期性,基音周期为67(样本点数)(2)/m/: 自相关函数具有周期性,基音周期为67(样本点数)(3)/n/ : 自相关函数具有周期性,基音周期为59(样本点数)可以看出/r/、/m/、/n/这几个因素的自相关函数图形有准周期性,并且有比较明显的峰值,所以为浊音。

《语音信号处理》课程笔记第一章语音信号处理的基础知识1.1 语音信号处理的发展历程语音信号处理的研究起始于20世纪50年代,最初的研究主要集中在语音合成和语音识别上。
在早期,由于计算机技术和数字信号处理技术的限制,语音信号处理的研究进展缓慢。
随着技术的不断发展,尤其是快速傅里叶变换(FFT)的出现,使得语音信号的频域分析成为可能,从而推动了语音信号处理的发展。
到了20世纪80年代,随着全球通信技术的发展,语音信号处理在语音编码和传输等领域也得到了广泛应用。
近年来,随着人工智能技术的快速发展,语音信号处理在语音识别、语音合成、语音增强等领域取得了显著的成果。
1.2 语音信号处理的总体结构语音信号处理的总体结构可以分为以下几个部分:(1)语音信号的采集和预处理:包括语音信号的采样、量化、预加重等操作,目的是提高语音信号的质量,便于后续处理。
(2)特征参数提取:从预处理后的语音信号中提取出能够反映语音特性的参数,如基频、共振峰、倒谱等。
(3)模型训练和识别:利用提取出的特征参数,通过机器学习算法训练出相应的模型,并进行语音识别、说话人识别等任务。
(4)后处理:对识别结果进行进一步的处理,如语法分析、语义理解等,以提高识别的准确性。
1.3 语音的发声机理和听觉机理语音的发声机理主要包括声带的振动、声道的共鸣和辐射等过程。
声带振动产生的声波通过声道时,会受到声道形状的影响,从而产生不同的音调和音质。
听觉机理是指人类听觉系统对声波的感知和处理过程,包括外耳、中耳、内耳和听觉中枢等部分。
1.4 语音的感知和信号模型语音的感知是指人类听觉系统对语音信号的识别和理解过程。
语音信号模型是用来描述语音信号特点和变化规律的数学模型,包括时域模型、频域模型和倒谱模型等。
这些模型为语音信号处理提供了理论基础和工具。
第二章语音信号的时域分析和短时傅里叶分析2.1 语音信号的预处理语音信号的预处理主要包括采样、量化、预加重等操作,目的是提高语音信号的质量,便于后续处理。

实验目的:理解和掌握基于能量和过零率的语音端点检测的方法和原理实验原理:语音端点检测就是指从包含语音的一段信号中确定出语音地起始点和结束点。
基于能量和过零率的语音端点检测方法采用两级判决法。
第一级:先根据语音短时能量选取较高门限T1,进行一次粗判,得AB点;然后由背景噪声的平均能量确定一个较低门限T2,并从A点往左、B点往右分别找到短时能量包络与门限T2相交点C与D。
第二级:以短时平均过零率为标准,从C往左、D往右找到短时平均过零率低于门限T3(由背景噪声的平均过零率所确定)的两点E、F,即为语音段的起止点。
实验内容:主程序:clear all;S=wavread('song.wav');%¶ÁÈëÉùÒôÎļþfigure(1);subplot(4,1,1);plot(S);title('Ô-ʼÓïºÅÐźÅ');N=wavread('noise.wav');%¶ÁÈë±³¾°ÔëÉùplot(N);s=fra(100,45,S);%fen zhenLs=length(s);s2=s.^2;soundenergy=sum(s2,2)%ÇóÒ»Ö¡µÄÄÜÁ¿;subplot(4,1,2);plot(soundenergy);title('Ô-ʼÓïÒô¶ÌʱÄÜÁ¿');averagesoundenergy=sum(soundenergy)/Ls;soundzcr=zcro(s);%Çó¹ýÁãÂÊsubplot(4,1,3);plot(soundzcr);title('Ô-ʼÓïÒô¹ýÁãÂÊ');averagesoundzcr=sum(soundzcr)/Ls;n=fra(100,45,N);Ln=length(n);n2=n.^2;noiseenergy=sum(n2,2);averagenoiseenergy=sum(soundenergy)/Ln;noisezcr=zcro(n);averagenoisezcr=sum(noisezcr)/Ln;A=1;B=1;for i=1:Lsif (soundenergy(i)>10*averagenoiseenergy) T1=i;break;endendfor i=Ls:-1:1if (soundenergy(i)>A*averagenoiseenergy) T2=i;break;endendfor i=1:T1if(soundzcr(i)>B*averagenoisezcr)E=i;break;endendfor i=Ls:-1:1if(soundzcr(i)>B*averagenoisezcr)F=i;break;endendE=45*E;F=45*F;duandianjianche=S(E:F,:);subplot(4,1,4);plot(duandianjianche);求过零率函数:function f=zcro(x)f=zeros(size(x,1),1);for i=1:size(x,1)z=x(i,:);for j=1:(length(z)-1);if z(j)*z(j+1)<0f(i)=f(i)+1;endendend分帧函数:function f=fra(len,inc,x)fh=fix(((size(x,1)-len)/inc)+1); f=zeros(fh,len);i=1;n=1;while i<=fhj=1;while j<=lenf(i,j)=x(n);j=j+1;n=n+1;endn=n-len+inc;i=i+1;end实验结果:结果为:实验总结:。
实验一基于 MATLAB 的语音信号时域特征分析操作:报告:一. 实验目的语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和变换域等处理方法,其中时域分析是最简单的方法,直接对语音信号的时域波形进行分析,提取的特征参数主要有语音的短时能量,短时平均过零率,短时自相关函数等。
本实验要求掌握时域特征分析原理,并利用已学知识,编写程序求解语音信号的短时过零率、短时能量、短时自相关特征,分析实验结果,并能掌握借助时域分析方法所求得的参数分析语音信号的基音周期及共振峰。
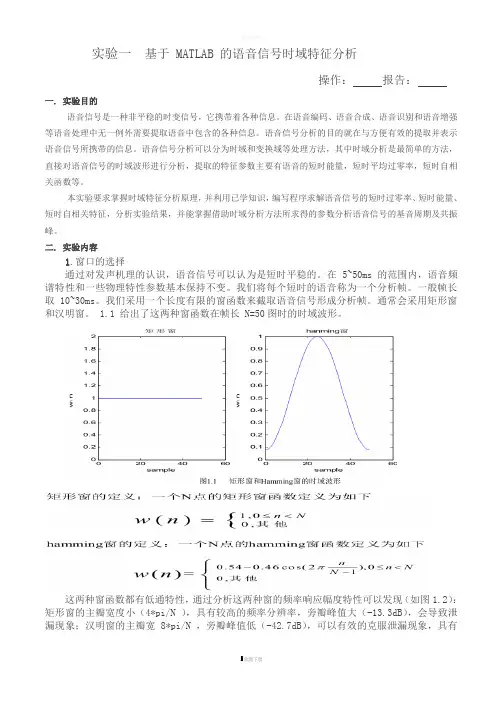
二. 实验内容1.窗口的选择通过对发声机理的认识,语音信号可以认为是短时平稳的。
在 5~50ms 的范围内,语音频谱特性和一些物理特性参数基本保持不变。
我们将每个短时的语音称为一个分析帧。
一般帧长取 10~30ms。
我们采用一个长度有限的窗函数来截取语音信号形成分析帧。
通常会采用矩形窗和汉明窗。
1.1 给出了这两种窗函数在帧长 N=50图时的时域波形。
这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发现(如图1.2):矩形窗的主瓣宽度小(4*pi/N ),具有较高的频率分辨率,旁瓣峰值大(-13.3dB),会导致泄漏现象;汉明窗的主瓣宽 8*pi/N ,旁瓣峰值低(-42.7dB),可以有效的克服泄漏现象,具有更平滑的低通特性。
因此在语音频谱分析时常使用汉明窗,在计算短时能量和平均幅度时通常用矩形窗。
2. 短时能量由于语音信号的能量随时间变化,清音和浊音之间的能量差别相当显著。
因此对语音的短时能量进行分析,可以描述语音的这种特征变化情况。
定义短时能量为:在用短时能量反映语音信号的幅度变化时,不同的窗函数以及相应窗的长短均有影响。
hamming 窗的效果比矩形窗略好。
语⾳信号处理实验⼀报告实验⼀语⾳信号的采集及预处理⼀、实验⽬的在理论学习的基础上,进⼀步地理解和掌握语⾳信号预处理及短时加窗的意义及基于matlab的实现⽅法。
⼆、实验原理及内容1、语⾳信号的录⾳、读⼊、放⾳等:练习matlab中⼏个⾳频处理函数,利⽤函数wavread对语⾳信号进⾏采样,记住采样频率和采样点数,给出以下语⾳的波形图(2.wav),wavread的⽤法参见mablab帮助⽂件。
利⽤wavplay或soundview 放⾳。
也可以利⽤wavrecord⾃⼰录制⼀段语⾳,并进⾏以上操作(需要话筒)。
I=wavread('2.wav');Fs=115200;soundview(I,Fs) %波形图如图1所⽰图1 2.wav的波形图利⽤wavplay函数,在佩戴⽿机的情况下可以清晰的听到所要播放于⼼的消息。
2、语⾳信号的分帧:对语⾳信号进⾏分帧,可以利⽤voicebox⼯具箱中的函数enframe。
voicebox⼯具箱是基于GNU协议的⾃由软件,其中包含了很多语⾳信号相关的函数。
voicebox⼯具箱安装⽅法:(1)把⼯具箱拷贝⼊C:\Program Files\MATLAB\R2006b\toolbox⽬录下;(2)菜单file-set path-"Add folder" 导⼊voicebox;图2 Set Path(3)菜单file-Preference-General-"Updata Toolbox Path Cache图3 Preferencesy=enframe(I,256,128);whos y I实验结果为:Name Size Bytes Class AttributesI 9000x1 72000 doubley 69x256 141312 doubleI=wavread('2.wav');t=enframe(I,256,128);plot(t)图4 分帧后的波形图3、语⾳信号的加窗:本步要求利⽤window函数设计窗⼝长度为256(N=256)的矩形窗(rectwin)、汉明窗(hamming)及汉宁窗(hann)),利⽤wvtool函数观察其时域波形图及频谱特性,⽐较得出结论。
语音信号处理实验报告要求第一篇:语音信号处理实验报告要求实验一:1.简述本次试验的目的,关于基音周期的理论;2.使用相关法的同学,给出程序的同时要说明所使用语音段的长度(短时平稳性),解释怎样在matlab中实现三电平削波(for...end 循环和if elseif else end判决的使用)。
给出清浊音两组截取后的语音信号波形图、三电平削波后的信号图、自相关计算后的信号图。
然后根据自相关信号图上最大峰值和次峰值之间的间隔点数,计算出基音周期和基音频率;3.使用倒谱法的同学,要解释分帧后加窗的方法,给出清浊音其中各一帧的语音信号波形图,和计算后的倒谱图。
并根据倒谱图上对应基音周期处的峰值的位置,给出基音周期。
4.使用简化逆滤波的同学,要说明切比雪夫2型低通滤波器的使用方法(cheby2、freqz两个函数的使用方法、参数意义),给出低通滤波后的信号波形图、5倍抽取后的波形图、自相关计算后信号波形图、5倍插值后的信号波形图,根据浊音内插后的信号图上最大峰值和次峰值之间的间隔点数计算基音周期;5.比较所选用的两种方法的结果。
实验二:1.给出倒谱法的程序,解释汉明窗宽度的选取要求(书上有简单解释),解释怎样实现倒谱窗的matlab编程方法和倒谱窗宽度的选取(男女生有一定的差别),给出加窗后的信号波形图、对数谱图、倒谱图、加窗后的信号频谱图,给出三个共振峰的估值。
2.给出LPC谱估计程序,不同LPC阶数时的LPC谱图,在n=?时,学生自己估计的前三个共振峰的值。
实验三:给出录音的内容,判断结果。
解释端点检测的原理、MFCC系数的说明和DTW算法的简单原理(参考书上都有比较详细的解释)。
识别的结果的表格和识别的结果正确率(正确的数目,错误的数目,正确率)。
考虑一下识别错误的原因(录音的效果?端点检测算法的可靠性?DTW算法的可靠性?等)第二篇:DSP语音信号处理摘要语音信号处理是研究数字信号处理技术和语音信号进行处理的一门学科,是一门新型的学科,是在多门学科基础上发展起来的综合性技术,它涉及到数字信号处理、模式识别、语言学。
实验一、语音信号采集与分析一、实验目的:1)了解语音信号处理基本知识:语音信号的生成的数学模型。
2)在理论学习的基础上,进一步地理解和掌握语音信号的读入、回放、波形显示。
语音信号时域和频域分析方法。
二、实验原理一定时宽的语音信号,其能量的大小随时间有明显的变化。
其中清音段(以清音为主要成份的语音段),其能量比浊音段小得多。
短时过零数也可用于语音信号分析中,发浊音时,其语音能量约集中于3kHz以下,而发清音时,多数能量出现在较高频率上,可认为浊音时具有较低的平均过零数,而清音时具有较高的平均过零数,因而,对一短时语音段计算其短时平均能量及短时平均过零数,就可以较好地区分其中的清音段和浊音段,从而可判别句中清、浊音转变时刻,声母韵母的分界以及无声与有声的分界。
这在语音识别中有重要意义。
FFT在数字通信、语音信号处理、图像处理、匹配滤波以及功率谱估计、仿真、系统分析等各个领域都得到了广泛的应用。
本实验通过分析加噪的语音信号频谱,可以作为分离信号和噪声的理论基础。
三、实验内容:Matlab编程实验步骤:1.新建M文件,扩展名为“.m”,编写程序;2.选择File/Save命令,将文件保存在F盘中;3.在Command Window窗中输入文件名,运行程序;程序一、用MATLAB对原始语音信号进行时域分析,分析短时平均能量及短时平均过零数。
程序二、用MATLAB对原始语音信号进行频域分析,画出它的时域波形和频谱给原始的语音信号加上一个高频余弦噪声,频率为5kHz。
画出加噪后的语音信号时域和频谱图。
程序1.a=wavread(' D:\II.wav'); %读取语音信号的数据,赋给变量x1,这里的文件的全路径和文件名由个人设计n=length(a);N=320;subplot(3,1,1),plot(a);h=linspace(1,1,N);%形成一个矩形窗,长度为NEn=conv(h,a.*a);%求卷积得其短时能量函数Ensubplot(3,1,2),plot(En);for i=1:n-1if a(i)>=0b(i)= 1;elseb(i) = -1;endif a(i+1)>=0b(i+1)=1;elseb(i+1)=-1;endw(i)=abs(b(i+1)-b(i));end%求出每相邻两点符号的差值的绝对值k=1;j=0;while (k+N-1)<nZm(k)=0;for i=0:N-1;Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+160; %每次移动半个窗endfor w=1:jQ(w)=Zm(160*(w-1)+1)/640;%短时平均过零率endsubplot(3,1,3),plot(Q);实验结果打印粘贴到右侧:程序2:fs=22050; %语音信号采样频率为22050x1=wavread('D:\II.wav'); %读取语音信号的数据,赋给变量x1sound(x1,22050); %播放语音信号f=fs*(0:511)/1024;t=0:1/22050:(size(x1)-1)/22050; %将所加噪声信号的点数调整到与原始信号相同Au=0.03;d=[Au*cos(2*pi*5000*t)]'; %噪声为5kHz的余弦信号x2=x1+d;sound(x2,22050); %播放加噪声后的语音信号y2=fft(x2,1024); %对信号做1024点FFT变换figure(1)subplot(2,1,1);plot(x1) %做原始语音信号的时域图形title('原始语音信号');xlabel('time n');ylabel('幅值 n');subplot(2,1,2);plot(t,x2)title('加噪后的信号');xlabel('time n');ylabel('幅值 n');figure(2)subplot(2,1,1);plot(f,abs(x1(1:512)));title('原始语音信号频谱');xlabel('Hz');ylabel('幅值');subplot(2,1,2);plot(f,abs(y2(1:512)));title('加噪后的信号频谱');xlabel('Hz'); ylabel('幅值');实验结果打印粘贴到右侧:050010001500200025003000350040004500原始语音信号time n幅值 n加噪后的信号time n幅值 n020004000600080001000012000原始语音信号频谱Hz幅值加噪后的信号频谱Hz幅值四、实验分析加入噪声后音频文件可辨性下降,波形的平缓,频谱图上看,能量大部分集中在2000HZz到4000Hz之间。
一、实验目的1. 理解语音信号处理的基本原理和流程。
2. 掌握语音信号的采集、预处理、特征提取和识别等关键技术。
3. 提高实际操作能力,运用所学知识解决实际问题。
二、实验原理语音信号处理是指对语音信号进行采集、预处理、特征提取、识别和合成等操作,使其能够应用于语音识别、语音合成、语音增强、语音编码等领域。
实验主要包括以下步骤:1. 语音信号的采集:使用麦克风等设备采集语音信号,并将其转换为数字信号。
2. 语音信号的预处理:对采集到的语音信号进行降噪、去噪、归一化等操作,提高信号质量。
3. 语音信号的特征提取:提取语音信号中的关键特征,如频率、幅度、倒谱等,为后续处理提供依据。
4. 语音信号的识别:根据提取的特征,使用语音识别算法对语音信号进行识别。
5. 语音信号的合成:根据识别结果,合成相应的语音信号。
三、实验步骤1. 语音信号的采集使用麦克风采集一段语音信号,并将其保存为.wav文件。
2. 语音信号的预处理使用MATLAB软件对采集到的语音信号进行预处理,包括:(1)降噪:使用谱减法、噪声抑制等算法对语音信号进行降噪。
(2)去噪:去除语音信号中的杂音、干扰等。
(3)归一化:将语音信号的幅度归一化到相同的水平。
3. 语音信号的特征提取使用MATLAB软件对预处理后的语音信号进行特征提取,包括:(1)频率分析:计算语音信号的频谱,提取频率特征。
(2)幅度分析:计算语音信号的幅度,提取幅度特征。
(3)倒谱分析:计算语音信号的倒谱,提取倒谱特征。
4. 语音信号的识别使用MATLAB软件中的语音识别工具箱,对提取的特征进行识别,识别结果如下:(1)将语音信号分为浊音和清音。
(2)识别语音信号的音素和音节。
5. 语音信号的合成根据识别结果,使用MATLAB软件中的语音合成工具箱,合成相应的语音信号。
四、实验结果与分析1. 语音信号的采集采集到的语音信号如图1所示。
图1 语音信号的波形图2. 语音信号的预处理预处理后的语音信号如图2所示。
语音信号处理实验指导书实验一:语音信号的采集与播放实验目的:了解语音信号的采集与播放过程,掌握采集设备的使用方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 将麦克风插入电脑的麦克风插孔。
2. 打开电脑的录音软件(如Windows自带的录音机)。
3. 在录音软件中选择麦克风作为录音设备。
4. 点击录音按钮开始录音,讲话或者唱歌几秒钟。
5. 点击住手按钮住手录音。
6. 播放刚刚录制的语音,检查录音效果。
7. 将扬声器或者耳机插入电脑的音频输出插孔。
8. 打开电脑的音频播放软件(如Windows自带的媒体播放器)。
9. 选择要播放的语音文件,点击播放按钮。
10. 检查语音播放效果。
实验二:语音信号的分帧与加窗实验目的:了解语音信号的分帧和加窗过程,掌握分帧和加窗算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 将处理后的语音帧进行播放,检查分帧和加窗效果。
实验三:语音信号的频谱分析实验目的:了解语音信号的频谱分析过程,掌握频谱分析算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 对每一帧的语音信号进行快速傅里叶变换(FFT)得到频谱。
5. 将频谱绘制成图象,观察频谱的特征。
6. 对频谱进行谱减法处理,去除噪声。
7. 将处理后的语音帧进行播放,检查频谱分析效果。
实验四:语音信号的降噪处理实验目的:了解语音信号的降噪处理过程,掌握降噪算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段带噪声的语音。
实验报告一、 实验目的、要求(1)掌握语音信号采集的方法(2)掌握一种语音信号基音周期提取方法(3)掌握短时过零率计算方法(4)了解Matlab 的编程方法二、 实验原理基本概念:(a )短时过零率:短时内, 信号跨越横轴的情况, 对于连续信号, 观察语音时域波形通过横轴的情况;对于离散信号, 相邻的采样值具有不同的代数符号, 也就是样点改变符号的次数。
对于语音信号, 是宽带非平稳信号, 应考察其短时平均过零率。
其中sgn[.]为符号函数⎪⎩⎪⎨⎧<=>=0 x(n)-1sgn(x(n))0 x(n)1sgn(x(n))短时平均过零的作用1.区分清/浊音:浊音平均过零率低, 集中在低频端;清音平均过零率高, 集中在高频端。
2.从背景噪声中找出是否有语音, 以及语音的起点。
(b )基音周期基音是发浊音时声带震动所引起的周期性, 而基音周期是指声带震动频率的倒数。
基音周期是语音信号的重要的参数之一, 它描述语音激励源的一个重要特征, 基音周期信息在多个领域有着广泛的应用, 如语音识别、说话人识别、语音分析与综合以及低码率语音编码, 发音系统疾病诊断、听觉残障者的语音指导等。
因为汉语是一种有调语言, 基音的变化模式称为声调, 它携带着非常重要的具有辨意作用的信息, 有区别意义的功能, 所以, 基音的提取和估计对汉语更是一个十分重要的问题。
由于人的声道的易变性及其声道持征的因人而异, 而基音周期的范围又很宽, 而同—个人在不同情态下发音的基音周期也不同, 加之基音周期还受到单词∑--=-=10)]1(sgn[)](sgn[21N m n n n m x m x Z发音音调的影响, 因而基音周期的精确检测实际上是一件比较困难的事情。
基音提取的主要困难反映在: ①声门激励信号并不是一个完全周期的序列, 在语音的头、尾部并不具有声带振动那样的周期性, 有些清音和浊音的过渡帧是很难准确地判断是周期性还是非周期性的。