2015年浙江省高考数学试卷(文科)答案与解析
- 格式:doc
- 大小:384.50 KB
- 文档页数:15
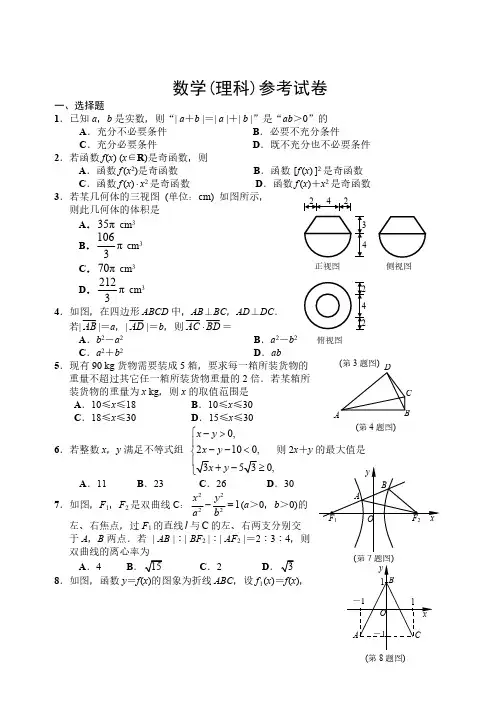

一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P=( )A .[)3,4B .(]2,3C .()1,2-D .(]1,3- 【答案】A 【解析】试题分析:由题意得,{}|31P x x x =≥≤或,所以[3,4)P Q =,故选A.考点:1.一元二次不等式的解法;2.集合的交集运算.2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A .83cm B .123cm C .3233cm D .4033cm 【答案】C考点:1.三视图;2.空间几何体的体积.3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 【答案】D考点:1.充分条件、必要条件;2.不等式的性质.4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m【答案】A 【解析】试题分析:采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.考点:直线、平面的位置关系. 5、函数()1cos f x x x x ⎛⎫=-⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( ) A . B . C . D . 【答案】D 【解析】试题分析:因为11()()cos ()cos ()f x x x x x f x x x-=-+=--=-,故函数是奇函数,所以排除A,B ;取x π=,则11()()cos ()0f ππππππ=-=--<,故选D.考点:1.函数的基本性质;2.函数的图象.6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m )分别为x ,y ,z ,且x y z <<,三种颜色涂料的粉刷费用(单位:元/2m )分别为a ,b ,c ,且a b c <<.在不同的方案中,最低的总费用(单位:元)是( )A .ax by cz ++B .az by cx ++C .ay bz cx ++D .ay bx cz ++ 【答案】B考点:1.不等式性质;2.不等式比较大小.7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支 【答案】C 【解析】试题分析:由题可知,当P 点运动时,在空间中,满足条件的AP 绕AB 旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C.考点:1.圆锥曲线的定义;2.线面位置关系. 8、设实数a ,b ,t 满足1sin a b t +==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin 2b唯一确定 D .若t 确定,则2a a +唯一确定 【答案】B 【解析】试题解析:因为1sin a b t +==,所以222(1)sin a b t +==,所以2221a a t +=-,故当t 确定时,21t -确定,所以22a a +唯一确定.故选B. 考点:函数概念二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:2log 2= ,24log 3log 32+= .【答案】12-考点:对数运算10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .【答案】2,13- 【解析】试题分析:由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d +=,所以121,3d a =-=. 考点:1.等差数列的定义和通项公式;2.等比中项.11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 .【答案】3,2π 【解析】试题分析:()211cos 2113sin sin cos 1sin 21sin 2cos 222222x f x x x x x x x -=++=++=-+3)242x π=-+,所以22T ππ==;min 3()22f x =-. 考点:1.三角函数的图象与性质;2.三角恒等变换.12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .【答案】162-考点:1.分段函数求值;2.分段函数求最值. 13、已知1e ,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b = .【解析】试题分析:由题可知,不妨1(1,0)e =,21(2e =,设(,)b x y =,则11b e x ⋅==,2112b e x y ⋅=+=,所以3(1,)3b =,所以113b =+=考点:1.平面向量数量积运算;2.向量的模.14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是 . 【答案】15 【解析】试题分析: 22,2224631034,22x y y xz x y x y x y y x +-≥-⎧=+-+--=⎨--<-⎩由图可知当22y x ≥-时,满足的是如图的AB 劣弧,则22z x y =+-在点(1,0)A 处取得最大值5;当22y x <-时,满足的是如图的AB 优弧,则1034z x y =--与该优弧相切时取得最大值,故1015z d -==,所以15z =,故该目标函数的最大值为15.考点:1.简单的线性规划;15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线by x c=的对称点Q 在椭圆上,则椭圆的离心率是 .考点:1.点关于直线对称;2.椭圆的离心率.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 16. (本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan(A)24π+=.(1)求2sin 2sin 2cos AA A+的值;(2)若B ,34a π==,求ABC ∆的面积.【答案】(1)25;(2)9考点:1.同角三角函数基本关系式;2.正弦定理;3.三角形面积公式.17. (本题满分15分)已知数列{}n a 和{}n b 满足,*1112,1,2(n N ),n n a b a a +===∈*12311111(n N )23n n b b b b b n+++++=-∈. (1)求n a 与n b ;(2)记数列{}n n a b 的前n 项和为n T ,求n T . 【答案】(1)2;n n n a b n ==;(2)1*(1)22()n n T n n N +=-+∈【解析】试题分析:(1)根据数列递推关系式,确定数列的特点,得到数列的通项公式;(2)根据(1)问得到新的数列的通项公式,利用错位相减法进行数列求和.考点:1.等差等比数列的通项公式;2.数列的递推关系式;3.错位相减法求和. 18. (本题满分15分)如图,在三棱锥111ABC A B C -中,011ABC=90=AC 2,AA 4,A ?=,AB 在底面ABC的射影为BC 的中点,D 为11B C 的中点. (1)证明: 11D A BC A ⊥平面; (2)求直线1A B 和平面11B C B C 所成的角的正弦值.【答案】(1)略;(2)作1A F DE ⊥,垂足为F ,连结BF. 因为AE ⊥平面1A BC ,所以1BC A E ⊥. 因为BC AE ⊥,所以BC ⊥平面1AA DE . 所以11,BC A F A F ⊥⊥平面11BB C C .所以1A BF ∠为直线1A B 与平面11BB C C 所成角的平面角.由2,90AB AC CAB ==∠=,得EA EB ==.由AE ⊥平面1A BC ,得1114,A A A B A E ==.由1114,90DE BB DA EA DA E ====∠=,得1A F =所以1sin 8A BF ∠=考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角. 19. (本题满分15分)如图,已知抛物线211C 4x :y=,圆222C (y 1)1x +-=:,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点.(1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点, 且与抛物线的对称轴不平行,则该直线 与抛物线相切,称该公共点为切点.【答案】(1)222222(2,),(,)11t t A t t B t t ++;(2)32t因为直线PA 与抛物线相切,所以216160k kt ∆=-=,解得k t =. 所以2x t =,即点2(2,)A t t .设圆2C 的圆心为(0,1)D ,点B 的坐标为00(,)x y ,由题意知,点B,O 关于直线PD 对称,故有00001220y x t x t y ⎧=-+⎪⎨⎪-=⎩,解得2002222,11t t x y t t ==++.即点22222(,)11t t B t t++. (2)由(1)知,AP = 直线AP 的方程为20tx y t --=, 所以点B 到直线PA的距离为2d =所以PAB ∆的面积为3122t S AP d =⋅=.考点:1.抛物线的几何性质;2.直线与圆的位置关系;3.直线与抛物线的位置关系. 20. (本题满分15分)设函数2(),(,)f x x ax b a b R =++∈.(1)当214a b =+时,求函数()f x 在[1,1]-上的最小值()g a 的表达式; (2)已知函数()f x 在[1,1]-上存在零点,021b a ≤-≤,求b 的取值范围.【答案】(1)222,2,4()1,22,2,24a a a g a a a a a ⎧++≤-⎪⎪⎪=-<≤⎨⎪⎪-+>⎪⎩;(2)[3,9-- 考点:1.函数的单调性与最值;2.分段函数;3.不等式性质;4.分类讨论思想.。

(完整版)2015年浙江省高考数学试卷及答案(文科)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)2015年浙江省高考数学试卷及答案(文科)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)2015年浙江省高考数学试卷及答案(文科)(word版可编辑修改)的全部内容。
绝密★考试结束前2015年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上.选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试题卷上。
参考公式 台体的体积公式121()3V h S S =其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高 柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh = 其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径 如果事件,A B 互斥 ,那么()()()P A B P A P B +=+一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P =( ) A .[)3,4 B .(]2,3 C .()1,2- D .(]1,3-2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A .83cm B .123cm C .3233cm D .4033cm3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m5、函数()1cos f x x x x ⎛⎫=- ⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m )分别为x ,y ,z ,且x y z <<,三种颜色涂料的粉刷费用(单位:元/2m )分别为a ,b ,c ,且a b c <<.在不同的方案中,最低的总费用(单位:元)是( )A .ax by cz ++B .az by cx ++C .ay bz cx ++D .ay bx cz ++ 7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支 8、设实数a ,b ,t 满足1sin a b t +==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin 2b 唯一确定 D .若t 确定,则2a a +唯一确定 二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.) 9、计算:22log = ,24log 3log 32+= . 10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 .12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .13、已知1e ,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b = .14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是 .15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线by x c=的对称点Q 在椭圆上,则椭圆的离心率是 .三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分14分)在ABC ∆中,内角A ,B,C 所对的边分别为,,a b c .已知tan(A)24π+=。

2015年普通高等学校招生全国统一考试(浙江卷) 数学(文科) 一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1、已知集合,,则() A. B. C. D. 2、某几何体的三视图如图所示(单位:),则该几何体的体积是() A. B. C. D. 3、设,是实数,则“”是“”的() A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 4、设,是两个不同的平面,,是两条不同的直线,且,() A.若,则 B.若,则 C.若,则 D.若,则 5、函数(且)的图象可能为() A. B. C. D. 6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:)分别为,,,且,三种颜色涂料的粉刷费用(单位:元/)分别为,,,且.在不同的方案中,最低的总费用(单位:元)是() A. B. C. D. 7、如图,斜线段与平面所成的角为,为斜足,平面上的动点满足,则点的轨迹是() A.直线 B.抛物线 C.椭圆 D.双曲线的一支 8、设实数,,满足() A.若确定,则唯一确定 B.若确定,则唯一确定 C.若确定,则唯一确定 D.若确定,则唯一确定 二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.) 9、计算:,. 10、已知是等差数列,公差不为零.若,,成等比数列,且,则,. 11、函数的最小正周期是,最小值是. 12、已知函数,则,的最小值是. 13、已知,是平面单位向量,且.若平面向量满足,则. 14、已知实数,满足,则的最大值是. 15、椭圆()的右焦点关于直线的对称点在椭圆上,则椭圆的离心率是.。

2015年浙江省高考数学试卷及答案(文科)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2015年浙江省高考数学试卷及答案(文科))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2015年浙江省高考数学试卷及答案(文科)的全部内容。
绝密★考试结束前2015年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2。
每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
参考公式 台体的体积公式121()3V h S S =其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高 柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh = 其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径 如果事件,A B 互斥 ,那么()()()P A B P A P B +=+一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P =( ) A .[)3,4 B .(]2,3 C .()1,2- D .(]1,3-2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( ) A .83cm B .123cm C .3233cm D .4033cm3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m5、函数()1cos f x x x x ⎛⎫=- ⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m )分别为x ,y ,z ,且x y z <<,三种颜色涂料的粉刷费用(单位:元/2m )分别为a ,b ,c ,且a b c <<.在不同的方案中,最低的总费用(单位:元)是( )A .ax by cz ++B .az by cx ++C .ay bz cx ++D .ay bx cz ++ 7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支 8、设实数a ,b ,t 满足1sin a b t +==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin 2b 唯一确定 D .若t 确定,则2a a +唯一确定 二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.) 9、计算:22log = ,24log 3log 32+= . 10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 .12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .13、已知1e ,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b = .14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是 .15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线by x c=的对称点Q 在椭圆上,则椭圆的离心率是 .三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分14分)在ABC ∆中,内角A,B ,C 所对的边分别为,,a b c 。

2015年普通高等学校招生全国统一考试数学文试题(浙江卷,含解析)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P=( )A .[)3,4B .(]2,3C .()1,2-D .(]1,3-【答案】A 【解析】试题分析:由题意得,{}|31P x x x =≥≤或,所以[3,4)P Q =,故选A.考点:1.一元二次不等式的解法;2.集合的交集运算.2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cmD .4033cm【答案】C考点:1.三视图;2.空间几何体的体积.3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 【答案】D考点:1.充分条件、必要条件;2.不等式的性质.4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m 【答案】A 【解析】试题分析:采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D中,//αβ时,,l m也可以异面.故选A.考点:直线、平面的位置关系.5、函数()1cosf x x xx⎛⎫=-⎪⎝⎭(xππ-≤≤且0x≠)的图象可能为()A. B. C. D.【答案】D【解析】试题分析:因为11()()cos()cos()f x x x x x f xx x-=-+=--=-,故函数是奇函数,所以排除A, B;取xπ=,则11()()cos()0fππππππ=-=--<,故选D.考点:1.函数的基本性质;2.函数的图象.6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m)分别为x,y,z,且x y z<<,三种颜色涂料的粉刷费用(单位:元/2m)分别为a,b,c,且a b c<<.在不同的方案中,最低的总费用(单位:元)是()A.ax by cz++ B.az by cx++ C.ay bz cx++ D.ay bx cz++【答案】B考点:1.不等式性质;2.不等式比较大小.7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支 【答案】C 【解析】试题分析:由题可知,当P 点运动时,在空间中,满足条件的AP 绕AB 旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C. 考点:1.圆锥曲线的定义;2.线面位置关系. 8、设实数a ,b ,t 满足1sin a b t+==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin2b唯一确定 D .若t 确定,则2a a +唯一确定【答案】B 【解析】试题解析:因为1sin a b t+==,所以222(1)sin a b t +==,所以2221a a t +=-,故当t 确定时,21t -确定,所以22a a +唯一确定.故选B.考点:函数概念二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:22log 2=,24log 3log 32+= .【答案】1,332-考点:对数运算10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a =,d = .【答案】2,13-【解析】试题分析:由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d +=,所以121,3d a =-=.考点:1.等差数列的定义和通项公式; 2.等比中项.11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 .【答案】32,2π-【解析】试题分析:()211cos 2113sin sin cos 1sin 21sin 2cos 222222x f x x x x x x x -=++=++=-+23sin(2)242x π=-+,所以22T ππ==;min 32()22f x =-. 考点:1.三角函数的图象与性质;2.三角恒等变换.12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .【答案】1;2662--考点:1.分段函数求值;2.分段函数求最值.13、已知1e,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b =.【答案】23【解析】试题分析:由题可知,不妨1(1,0)e =,213(,)22e =,设(,)b x y =,则11b e x ⋅==,213122b e x y ⋅=+=,所以3(1,)3b =,所以123133b =+=. 考点:1.平面向量数量积运算;2.向量的模.14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是 . 【答案】15 【解析】试题分析:22,2224631034,22x y y xz x y x y x y y x +-≥-⎧=+-+--=⎨--<-⎩ 由图可知当22y x ≥-时,满足的是如图的AB 劣弧,则22z x y =+-在点(1,0)A 处取得最大值5;当22y x <-时,满足的是如图的AB 优弧,则1034z x y =--与该优弧相切时取得最大值,故1015z d -==,所以15z =,故该目标函数的最大值为15.考点:1.简单的线性规划;15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线b y xc =的对称点Q 在椭圆上,则椭圆的离心率是 .【答案】22考点:1.点关于直线对称;2.椭圆的离心率.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 16. (本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan(A)24π+=.(1)求2sin 2sin 2cos AA A 的值;(2)若B ,34a π==,求ABC ∆的面积.【答案】(1)25;(2)9考点:1.同角三角函数基本关系式;2.正弦定理;3.三角形面积公式.17. (本题满分15分)已知数列na 和nb 满足,*1112,1,2(n N ),n n a b a a +===∈*12311111(n N )23n n b b b b b n +++++=-∈.(1)求na 与nb ;(2)记数列n n a b 的前n 项和为nT ,求nT .【答案】(1)2;n n n a b n ==;(2)1*(1)22()n n T n n N +=-+∈【解析】试题分析:(1)根据数列递推关系式,确定数列的特点,得到数列的通项公式;(2)根据(1)问得到新的数列的通项公式,利用错位相减法进行数列求和.考点:1.等差等比数列的通项公式;2.数列的递推关系式;3.错位相减法求和.18. (本题满分15分)如图,在三棱锥111ABCA B C 中,011ABC=90=AC 2,AA 4,A ,AB 在底面ABC 的射影为BC 的中点,D 为11B C 的中点.(1)证明: 11D A BC A 平面; (2)求直线1A B和平面11B C B C 所成的角的正弦值.【答案】(1)略;(2)7(2)作1A F DE⊥,垂足为F,连结BF.因为AE⊥平面1A BC,所以1BC A E⊥.因为BC AE⊥,所以BC⊥平面1AA DE.所以11,BC A F A F⊥⊥平面11BB C C.所以1A BF∠为直线1A B与平面11BB C C所成角的平面角.由2,90AB AC CAB==∠=,得2EA EB==.由AE ⊥平面1A BC,得1114,14A A A B A E ===.由1114,2,90DE BB DA EA DA E ====∠=,得172A F =.所以17sin 8A BF ∠=考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角.19. (本题满分15分)如图,已知抛物线211C 4x :y=,圆222C (y 1)1x :,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点.(1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点, 且与抛物线的对称轴不平行,则该直线 与抛物线相切,称该公共点为切点.【答案】(1)222222(2,),(,)11t t A t t B t t ++;(2)32t因为直线PA 与抛物线相切,所以216160k kt ∆=-=,解得k t =.所以2x t =,即点2(2,)A t t . 设圆2C 的圆心为(0,1)D ,点B 的坐标为00(,)x y ,由题意知,点B,O 关于直线PD 对称,故有00001220y x t x t y ⎧=-+⎪⎨⎪-=⎩,解得2002222,11t t x y t t ==++.即点22222(,)11t t B t t ++. (2)由(1)知,21AP t =+,直线AP 的方程为20tx y t --=, 所以点B 到直线PA 的距离为221d t =+.所以PAB ∆的面积为3122t S AP d =⋅=. 考点:1.抛物线的几何性质;2.直线与圆的位置关系;3.直线与抛物线的位置关系.20. (本题满分15分)设函数2(),(,)f x x ax b a b R =++∈. (1)当214a b时,求函数()f x 在[1,1]上的最小值()g a 的表达式;(2)已知函数()f x在[1,1]上存在零点,021b a≤-≤,求b的取值范围.【答案】(1)222,2,4()1,22,2,24aa ag a aaa a⎧++≤-⎪⎪⎪=-<≤⎨⎪⎪-+>⎪⎩;(2)[3,945]--考点:1.函数的单调性与最值;2.分段函数;3.不等式性质;4.分类讨论思想.。

2015年普通高等学校招生全国统一考试数学文试题(浙江卷,含解析)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P=( )A .[)3,4 B .(]2,3 C .()1,2- D .(]1,3- 【答案】A 【解析】试题分析:由题意得,{}|31P x x x =≥≤或,所以[3,4)P Q =,故选A.考点:1.一元二次不等式的解法;2.集合的交集运算. 2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cmD .4033cm【答案】C考点:1.三视图;2.空间几何体的体积.3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】D考点:1.充分条件、必要条件;2.不等式的性质.4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m 【答案】A 【解析】试题分析:采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.考点:直线、平面的位置关系.5、函数()1cos f x x xx ⎛⎫=- ⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )A .B .C .D .【答案】D 【解析】试题分析:因为11()()cos ()cos ()f x x x x x f x x x -=-+=--=-,故函数是奇函数,所以排除A, B ;取x π=,则11()()cos ()0f ππππππ=-=--<,故选D.考点:1.函数的基本性质;2.函数的图象. 6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m )分别为x ,y ,z ,且x y z <<,三种颜色涂料的粉刷费用(单位:元/2m )分别为a ,b ,c ,且a b c <<.在不同的方案中,最低的总费用(单位:元)是( )A .ax by cz ++B .az by cx ++C .ay bz cx ++D .ay bx cz ++ 【答案】B考点:1.不等式性质;2.不等式比较大小.7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支 【答案】C 【解析】试题分析:由题可知,当P 点运动时,在空间中,满足条件的AP 绕AB 旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C. 考点:1.圆锥曲线的定义;2.线面位置关系. 8、设实数a ,b ,t 满足1sin a b t+==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin2b唯一确定 D .若t 确定,则2a a +唯一确定【答案】B 【解析】 试题解析:因为1sin a b t+==,所以222(1)sin a b t +==,所以2221a a t +=-,故当t 确定时,21t -确定,所以22a a +唯一确定.故选B.考点:函数概念二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:2log 2=,24log 3log 32+= .【答案】12-考点:对数运算 10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .【答案】2,13-【解析】试题分析:由题可得,2111(2)()(6)a d a d a d +=++,故有1320a d +=,又因为1221a a +=,即131a d +=,所以121,3d a =-=.考点:1.等差数列的定义和通项公式;2.等比中项. 11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 .【答案】3,2π【解析】试题分析:()211cos 2113sin sin cos 1sin 21sin 2cos 222222x f x x x x x x x -=++=++=-+3)242x π=-+,所以22T ππ==;min 3()22f x =-. 考点:1.三角函数的图象与性质;2.三角恒等变换.12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .【答案】162-考点:1.分段函数求值;2.分段函数求最值.13、已知1e ,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b =.【答案】【解析】试题分析:由题可知,不妨1(1,0)e =,21(,22e =,设(,)b x y =,则11b e x ⋅==,2112b e x y ⋅==,所以3(1,)b =,所以11b =+=. 考点:1.平面向量数量积运算;2.向量的模.14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是. 【答案】15【解析】试题分析:22,2224631034,22x y y xz x y x y x y y x +-≥-⎧=+-+--=⎨--<-⎩ 由图可知当22y x ≥-时,满足的是如图的AB 劣弧,则22z x y =+-在点(1,0)A 处取得最大值5;当22y x <-时,满足的是如图的AB 优弧,则1034z x y =--与该优弧相切时取得最大值,故1015z d -==,所以15z =,故该目标函数的最大值为15.考点:1.简单的线性规划;15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线b y x c =的对称点Q 在椭圆上,则椭圆的离心率是 .【答案】2考点:1.点关于直线对称;2.椭圆的离心率.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16. (本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan(A)24π+=. (1)求2sin 2sin 2cos AA A +的值;(2)若B ,34a π==,求ABC ∆的面积.【答案】(1)25;(2)9考点:1.同角三角函数基本关系式;2.正弦定理;3.三角形面积公式.17. (本题满分15分)已知数列{}n a 和{}n b 满足,*1112,1,2(n N ),n n a b a a +===∈ *12311111(n N )23n n b b b b b n +++++=-∈.(1)求n a 与n b ;(2)记数列{}n n a b 的前n 项和为n T ,求n T .【答案】(1)2;n n n a b n ==;(2)1*(1)22()n n T n n N +=-+∈ 【解析】试题分析:(1)根据数列递推关系式,确定数列的特点,得到数列的通项公式;(2)根据(1)问得到新的数列的通项公式,利用错位相减法进行数列求和.考点:1.等差等比数列的通项公式;2.数列的递推关系式;3.错位相减法求和. 18.(本题满分15分)如图,在三棱锥111ABC A B C -中,011ABC=90=AC 2,AA 4,A ?=,AB 在底面ABC 的射影为BC 的中点,D 为11B C 的中点.(1)证明: 11D A BC A 平面; (2)求直线1A B 和平面11B C B C 所成的角的正弦值.【答案】(1)略;(2)(2)作1A F DE ⊥,垂足为F ,连结BF.因为AE ⊥平面1A BC ,所以1BC A E ⊥.因为BC AE ⊥,所以BC ⊥平面1AA DE .所以11,BC A F A F ⊥⊥平面11BB C C .所以1A BF ∠为直线1A B 与平面11BB C C 所成角的平面角.由2,90AB AC CAB ==∠=,得EA EB ==.由AE ⊥平面1A BC ,得1114,A A AB A E ===.由1114,90DE BB DA EA DA E ===∠=,得1A F =.所以1sin A BF ∠=考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角.19. (本题满分15分)如图,已知抛物线211C 4x :y=,圆222C (y 1)1x +-=:,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点.(1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线 与抛物线相切,称该公共点为切点.【答案】(1)222222(2,),(,)11t t A t t B t t ++;(2)32t因为直线PA 与抛物线相切,所以216160k kt ∆=-=,解得k t =.所以2x t =,即点2(2,)A t t . 设圆2C 的圆心为(0,1)D ,点B 的坐标为00(,)x y ,由题意知,点B,O 关于直线PD 对称,故有00001220y x t x t y ⎧=-+⎪⎨⎪-=⎩,解得2002222,11t t x y t t ==++.即点22222(,)11t t B t t ++.(2)由(1)知,AP =直线AP 的方程为20tx y t --=, 所以点B 到直线PA的距离为2d =.所以PAB ∆的面积为3122t S AP d =⋅=. 考点:1.抛物线的几何性质;2.直线与圆的位置关系;3.直线与抛物线的位置关系.20. (本题满分15分)设函数2(),(,)f x x ax b a b R =++∈. (1)当214a b =+时,求函数()f x 在[1,1]-上的最小值()g a 的表达式;(2)已知函数()f x 在[1,1]-上存在零点,021b a ≤-≤,求b 的取值范围.【答案】(1)222,2,4()1,22,2,24a a a g a a a a a ⎧++≤-⎪⎪⎪=-<≤⎨⎪⎪-+>⎪⎩;(2)[3,945]--考点:1.函数的单调性与最值;2.分段函数;3.不等式性质;4.分类讨论思想.。

2015年普通高等学校招生全国统一考试(浙江卷)文科数学1. 解析 {1P x x=-或}3x,所以[)34P Q =, .故选A.2. 解析 该几何体是棱长为2的正方体和底面边长为2、高为2的正四棱锥的组合体,所以3213222233V =+⨯⨯=.故选C . 3. 解析 取3a =,2b =-,所以0a b +>0ab >;反之取1a =-,2b =-,所以00ab a b >+>.故选D.4. 解析 由面面垂直判定定理知,A 正确.故选A.5. 解析 ()f x 是奇函数,排除A ,B ;当0x >, x 趋于0时,1x x-→-∞,cos 1x →,所以1cos x x x ⎛⎫-→-∞ ⎪⎝⎭.故选D. 6. 解析 解法一 特殊值:1x =,2y =,3z =,所以1a =,2b =,3c =.故选B. 解法二 利用排序不等式,最小的值是反序和.故选B.7. 解析 若30PAB ∠=,则AP 绕点A 旋转形成圆锥面,这面被平面α截得图象是椭圆.故选C.8. 解析 若t 确定,则2221a a t ++=,所以2221a a t +=-唯一确定.故选B. 9. 解析12221log log 22-==-,3222423log 3log 3log 3log 32222+=== 10. 解析 23271221a a a a a ⎧=⋅⎨+=⎩,所以()()()211112631a d a d a d a d ⎧+=++⎪⎨+=⎪⎩ , 所以1231a d ⎧=⎪⎨⎪=-⎩.11. 解析 ()1cos 21π3sin 2122242x f x x x -⎛⎫=++=-+ ⎪⎝⎭, 所以2ππ2T ==,()min 32f x =. 12. 解析 ()()61244642f f f -==+-=-⎡⎤⎣⎦, 当1x时,()()min 00f x f ==;当1x >时,()min 6f x =.综上所述,()min 6f x =.13. 解析 设1e OA =,2e OB =,由2e OB =得121cos e e 2=,,即12πe e 3=,.又12e e ⋅=⋅b b ,得12e e 0⋅-⋅=b b ,即()12e e 0⋅-=b ,故()12e e ⊥-b .过点O 作直线l AB ⊥,如图所示,因为1e 1⋅=b ,2e 1⋅=b ,据平面向量数量积的几何意义知,OC 在OA ,OB 上的投影均为1,所以12cos30OC ==故3=b .14. 解析 依题意知,240x y +-<,630x y -->,则2463x y x y +-+--=42631034x y x y x y --+--=--.令1034z x y =--,即34100x y z ++-=,且221x y +,因此圆心()00,到直线34100x y z ++-=的距离小于等于1,即1015z -,得515z ,所以z 的最大值为15,即2463x y x y +-+--的最大值为15.15. 解析 解法一 设()00Q x y ,,则12πe e 3=,OQ OF c ==,所以22200x y c +=,又2200221x y a b +=,所以()()22222220222a c b a c b x a b c--==-,所以4222002b y c x c =-=,所以2b yc =,不妨取0x =,所以QF 中点0022x c y +⎛⎫⎪⎝⎭,,代入00b y x c =, 得2bc c -=,化简得2220()b bc c b c ⎧++=⎪⎨≠⎪⎩舍去或b c =,所以2e =. 解法二 设椭圆的左焦点为1F ,依题意,1OF OQ OF ==,故112OQ FF =,且O 为1FF的中点,因此1FFQ △为Rt △,且1π2F QF ∠=,即1F Q FQ ⊥,则1F Q 所在直线斜率为 cb ,所以()0Q b ,,则1FQF △为等腰直角三角形,故b c =,2c e a ===. 16. 解析 (1) πtan tanπ1tan 4tan 2π41tan 1tan tan 4A A A AA ++⎛⎫+=== ⎪-⎝⎭-,得1tan 3A =. 2212sin 22sin cos 2tan 231sin 2cos 2sin cos cos 2tan 15213A A A A A A A A A A ⨯====+++⨯+.(2) sin 10A =,cos 10A =.由正弦定理得,sin sin a b AB =,所以b AC ==,又()sin sin sin cos cos sin 210105C A B A B A B =+=+=+=⎝⎭,所以11sin 39225ABC S ab C ==⨯⨯=△. 17. 解析 (1)由题意知{}n a 是等比数列,12a =,2q =,所以2nn a =.当2n 时,()*231111111231n n b b b b n b n -++++=-∈-N ,所以11n n n b b b n +=-,所以11n n n b b n ++=,所以12112n n b b b n n+====+,又11b =,所以n b n =.(或采用累乘法) (2)212222n n T n =⨯+⨯++⋅,所以()21212122n n n T n n +=⨯++-⨯+⋅, 所以()()()2111212122222212212n n n n n n T n n n +++--=+++-⋅=-=---,所以()1122n n T n +=-+.18. 解析 (1) 记BC 中点E ,连AE ,DE ,1A E .因为AB AC =,所以AE BC ⊥,又1A E ⊥面ABC ,AE ⊂面ABC ,所以1AE A E ⊥,又1BCA E E =,所以AE ⊥面1A BC ,又1=//AA DE ,所以1AEDA 是平行四边形,所以1//AE A D ,所以1A D ⊥面1A BC .(2)作1A F DE ⊥,垂足F ,连BF .因为1A D ⊥面1A BC ,所以1BC A D ⊥,又1BC A E ⊥,111A EA D A =,所以BC ⊥面1A DE ,又1A F ⊂面1A DE ,所以1BC A F ⊥,又DEBC E =,所以1A F ⊥面11BB C C ,所以1A BF ∠是直线1A B 和平面11BB C C 所成的角.经计算得1A D =,14A B =,1A E =11142A E A D A F DE ⋅===,所以1112sin 4A F A BF A B ∠===.19. 解析 (1)设直线AP 的方程为:()y k x t =-,联立214y x =,得2104x kx kt -+=,由直线AP 与抛物线1C 相切知,0∆=,又0k ≠,求得k t =,因为12y x t '==,所以2x t =,2y t =,所以()22A t t ,.设()00B x y ,,代入圆222(1)1C x y :,得20002x y y ,因为BP 为圆2C 的切线,所以21BP BC k k ⋅=-1==-,解得2221t y t =+,所以 0221tx t =+,所以2222211t t B t t ⎛⎫ ⎪++⎝⎭,. (2)B 到AP的距离2d ==12AB x =-=所以23111222PABS AB d t t =⋅==△. 20. 解析 (1) ()2221142a a f x x ax x ⎛⎫=+++=++ ⎪⎝⎭,对称轴2a x =-.当12a -<-,即2a >时,()()21124a g a f ab a =-=-+=-+;当112a--,即22a-时,()12a g a f ⎛⎫=-= ⎪⎝⎭;当12a ->,即2a <-时,()()2124a g a f a ==++ .综上所述,()22224122224a a a g a a a a a ⎧-+>⎪⎪⎪=-⎨⎪⎪++<-⎪⎩,, ,.(2)假设()f x 在[]11-,上的零点0x ,则2000x ax b ++=,所以[]2200001124a a b x ax x x ⎛⎫=--=-++∈- ⎪⎝⎭,,,对称轴直线02a x =-.当12a-<-,即2a >时,11a b a ---,综合221a b a +,得b ∈Φ; 当102a--<,即02a <时,214a a b--,综合221a ba +,得b ∈Φ;当012a -,即20a -时,214a ab -,综合221a b a +,得3945b--当12a->,即2a <-时,11a b a ---,综合221a b a +,得b ∈Φ.综上所述,3945b--。

2015年浙江省高考数学试卷(文科)一、选择题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合P={x|x2﹣2x≥3},Q={x|2<x<4},则P∩Q=()A.[3,4) B.(2,3]C.(﹣1,2)D.(﹣1,3]2.(5分)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.D.3.(5分)设a,b是实数,则“a+b>0”是“ab>0”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.(5分)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β,()A.若l⊥β,则α⊥βB.若α⊥β,则l⊥m C.若l∥β,则α∥βD.若α∥β,则l∥m5.(5分)函数f(x)=﹣(x﹣)cosx(﹣π≤x≤π且x≠0)的图象可能为()A.B.C.D.6.(5分)有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b <c.在不同的方案中,最低的总费用(单位:元)是()A.ax+by+cz B.az+by+cx C.ay+bz+cx D.ay+bx+cz7.(5分)如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支8.(5分)设实数a,b,t满足|a+1|=|sinb|=t.则()A.若t确定,则b2唯一确定B.若t确定,则a2+2a唯一确定C.若t确定,则sin唯一确定D.若t确定,则a2+a唯一确定二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)9.(6分)计算:log2=,2=.10.(6分)已知{a n}是等差数列,公差d不为零,若a2,a3,a7成等比数列,且2a1+a2=1,则a1=,d=.11.(6分)函数f(x)=sin2x+sinxcosx+1的最小正周期是,最小值是.12.(6分)已知函数f(x)=,则f(f(﹣2))=,f(x)的最小值是.13.(4分)已知1,2是平面单位向量,且1•2=,若平面向量满足•1=•=1,则||=.14.(4分)已知实数x,y满足x2+y2≤1,则|2x+y﹣4|+|6﹣x﹣3y|的最大值是.15.(4分)椭圆+=1(a>b>0)的右焦点F(c,0)关于直线y=x的对称点Q在椭圆上,则椭圆的离心率是.三、解答题:本大题共5小题,共74分。


专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = (x1)(x+2),则f(1)的值为()A. 1B. 0C. 1D. 22. 在等差数列{an}中,若a1=3,a3=9,则公差d为()A. 2B. 3C. 4D. 63. 下列函数中,既是奇函数又是偶函数的是()A. y = x²B. y = x³C. y = |x|D. y = cos(x)4. 在三角形ABC中,若a=8, b=10, sinA=3/5,则三角形ABC的面积S为()A. 12B. 24C. 36D. 485. 若复数z满足|z1|=|z+1|,则z在复平面上的对应点位于()A. 实轴上B. 虚轴上C. 原点D. 以原点为圆心,半径为1的圆上二、判断题(每题1分,共5分)1. 任何两个实数的和都是实数。
()2. 若a|b|=|a||b|,则a和b必须同号。
()3. 一元二次方程的判别式大于0时,方程有两个不相等的实数根。
()4. 在等差数列中,若公差为0,则数列中的所有项相等。
()5. 直线y=2x+1的斜率为2。
()三、填空题(每题1分,共5分)1. 若log₂x=3,则x=____。
2. 等差数列的前n项和公式为____。
3. 若a+b=5,ab=3,则a²+b²=____。
4. 圆的标准方程为____。
5. 若sinθ=1/2,且θ为锐角,则θ=____度。
四、简答题(每题2分,共10分)1. 简述等差数列的定义。
2. 请写出圆的周长和面积公式。
3. 什么是一元二次方程的判别式?4. 请解释什么是反函数。
5. 简述概率的基本性质。
五、应用题(每题2分,共10分)1. 解方程:2x²5x+3=0。
2. 计算等差数列1, 4, 7, 10, 的第10项。
3. 求函数f(x) = x²4x+3的顶点坐标。
4. 在直角坐标系中,点A(2,3)和点B(4,1),求线段AB的中点坐标。
2015浙江高考文科数学试题及答案一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P =( )A .[)3,4B .(]2,3C .()1,2-D .(]1,3-2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cm C .3233cm D .4033cm 3、设a ,b 是实数,则“0a b +>”是“0ab >”的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( )A .若l β⊥,则αβ⊥B .若αβ⊥,则l m ⊥C .若//l β,则//αβD .若//αβ,则//l m5、函数()1cos f x x x x ⎛⎫=- ⎪⎝⎭(x ππ-≤≤且0x ≠)的图象可能为( )A .B .C .D .6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:2m )分别为x ,y ,z ,且x y z <<,三种颜色涂料的粉刷费用(单位:元/2m )分别为a ,b ,c ,且a b c <<.在不同的方案中,最低的总费用(单位:元)是( )A .ax by cz ++B .az by cx ++C .ay bz cx ++D .ay bx cz ++7、如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支8、设实数a ,b ,t 满足1sin a b t +==( )A .若t 确定,则2b 唯一确定B .若t 确定,则22a a +唯一确定C .若t 确定,则sin 2b 唯一确定 D .若t 确定,则2a a +唯一确定 二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:2log = ,24log 3log 32+= . 10、已知{}n a 是等差数列,公差d 不为零.若2a ,3a ,7a 成等比数列,且1221a a +=,则1a = ,d = .11、函数()2sin sin cos 1f x x x x =++的最小正周期是 ,最小值是 . 12、已知函数()2,166,1x x f x x x x ⎧≤⎪=⎨+->⎪⎩,则()2f f -=⎡⎤⎣⎦ ,()f x 的最小值是 .13、已知1e ,2e 是平面单位向量,且1212e e ⋅=.若平面向量b 满足121b e b e ⋅=⋅=,则b = . 14、已知实数x ,y 满足221x y +≤,则2463x y x y +-+--的最大值是 .15、椭圆22221x y a b +=(0a b >>)的右焦点()F ,0c 关于直线b y x c=的对称点Q 在椭圆上,则椭圆的离心率是 .三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan(A)24π+=. (1)求2sin 2sin 2cos A A A的值; (2)若B ,34a π==,求ABC ∆的面积.17.(本题满分15分)已知数列n a 和n b 满足,*1112,1,2(n N ),n n a b a a +===∈*12311111(n N )23n n b b b b b n+++++=-∈.(1)求n a 与n b ;(2)记数列n n a b 的前n 项和为n T ,求n T .18.(本题满分15分)如图,在三棱锥111ABCA B C 中,011ABC=90=AC 2,AA 4,A ,AB 在底面ABC 的射影为BC 的中点,D 为11B C 的中点.(1)证明: 11D A BC A ⊥平面;(2)求直线1A B 和平面11B C B C 所成的角的正弦值.19.(本题满分15分)如图,已知抛物线211C 4x :y=,圆222C (y 1)1x :,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点.(1)求点A ,B 的坐标;(2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公共点为切点.20.(本题满分15分)设函数2(),(,)f x x ax b a b R =++∈. (1)当214a b 时,求函数()f x 在[1,1]上的最小值()g a 的表达式; (2)已知函数()f x 在[1,1]上存在零点,021b a ≤-≤,求b 的取值范围.。
2015高考真题——数学文(浙江卷)Word版含答案2015年普通高等学校招生全国统一考试(浙江卷)数学(文科)一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合,,则()A.B.C.D.2、某几何体的三视图如图所示(单位:),则该几何体的体积是()A.B.C.D.3、设,是实数,则""是""的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4、设,是两个不同的平面,,是两条不同的直线,且,()A.若,则B.若,则C.若,则D.若,则5、函数(且)的图象可能为()A.B.C.D.6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:)分别为,,,且,三种颜色涂料的粉刷费用(单位:元/)分别为,,,且.在不同的方案中,最低的总费用(单位:元)是()A.B.C.D.7、如图,斜线段与平面所成的角为,为斜足,平面上的动点满足,则点的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支8、设实数,,满足()A.若确定,则唯一确定B.若确定,则唯一确定C.若确定,则唯一确定D.若确定,则唯一确定二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:,.10、已知是等差数列,公差不为零.若,,成等比数列,且,则,.11、函数的最小正周期是,最小值是.12、已知函数,则,的最小值是.13、已知,是平面单位向量,且.若平面向量满足,则.14、已知实数,满足,则的最大值是.15、椭圆()的右焦点关于直线的对称点在椭圆上,则椭圆的离心率是.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分14分)在中,内角A,B,C所对的边分别为.已知.(1)求的值;(2)若,求的面积.17.(本题满分15分)已知数列和满足,.(1)求与;(2)记数列的前n项和为,求.18.(本题满分15分)如图,在三棱锥中,在底面ABC的射影为BC的中点,D为的中点.(1)证明: ;(2)求直线和平面所成的角的正弦值.19.(本题满分15分)如图,已知抛物线,圆,过点作不过原点O的直线PA,PB分别与抛物线和圆相切,A,B为切点.(1)求点A,B的坐标;(2)求的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公共点为切点.20.(本题满分15分)设函数.(1)当时,求函数在上的最小值的表达式;(2)已知函数在上存在零点,,求b的取值范围.2015年普通高等学校招生全国统一考试(浙江卷)数学(文科)参考答案一、选择题1. A2.C3.D4.A5.D6.B7.C8.B二、填空题9.【答案】10.【答案】11.【答案】12.【答案】13.【答案】14.【答案】1515.【答案】三、解答题16. 【答案】(1);(2)9(1)利用两角和与差的正切公式,得到t,利用同角三角函数基本函数关系式得到结论;(2)利用正弦原理得到边b的值,根据三角形,两边一夹角的面积公式计算得到三角形的面积试题解析:(1)由t所以(2) 由t可得,s.由正弦定理知:b=3又所以S?=×3×3×=917. 【答案】(1);(2)(1)由得当n=1时,故当n时,整理得所以(2)由(1)知,所以所以18. 【答案】(1)略;(2)(1)设E为BC中点,由题意得所以因为所以所以平面由D,E分别为的中点,得从而DE//且DE=所以是平行四边形,所以因为平面所以平面(2)作,垂足为F,连结BF.因为平面,所以.因为,所以平面.所以平面.所以为直线与平面所成角的平面角.由,得.由平面,得.由,得.所以19. 【答案】(1);(2)(1)由题意可知,直线PA的斜率存在,故可设直线PA的方程为所以消去y,整理得:因为直线PA与抛物线相切,所以,解得.所以,即点.设圆的圆心为,点的坐标为,由题意知,点B,O关于直线PD对称,故有,解得.即点.(2)由(1)知,,直线AP的方程为,所以点B到直线PA的距离为.所以的面积为.20. 【答案】(1);(2)(1)当时,故其对称轴为当时,当-2当>2时,g综上所述,(2)设s,t为方程的解,且-1,则由于,因此当时,由于和所以当-1由于综上可知,b的取值范围是。
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}223x x x P =-≥,{}Q 24x x =<<,则Q P=( )A .[)3,4B .(]2,3C .()1,2-D .(]1,3- 【答案】A 【解析】试题分析:由题意得,{}|31P x x x =≥≤或,所以[3,4)P Q =,故选A.考点:1.一元二次不等式的解法;2.集合的交集运算.2、某几何体的三视图如图所示(单位:cm ),则该几何体的体积是( )A .83cmB .123cmC .3233cm D .4033cm 【答案】C考点:1.三视图;2.空间几何体的体积.3、设a ,b 是实数,则“0a b +>”是“0ab >”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】D考点:1.充分条件、必要条件;2.不等式的性质.4、设α,β是两个不同的平面,l ,m 是两条不同的直线,且l α⊂,m β⊂( ) A .若l β⊥,则αβ⊥ B .若αβ⊥,则l m ⊥ C .若//l β,则//αβ D .若//αβ,则//l m 【答案】A 【解析】试题分析:采用排除法,选项A 中,平面与平面垂直的判定,故正确;选项B 中,当αβ⊥时,,l m 可以垂直,也可以平行,也可以异面;选项C 中,//l β时,,αβ可以相交;选项D 中,//αβ时,,l m 也可以异面.故选A.考点:直线、平面的位置关系. 5、函数(且)的图象可能为( )A .B .C .D . 【答案】D 【解析】试题分析:因为,故函数是奇函数,所以排除A, B ;取,则,故选D. 考点:1.函数的基本性质;2.函数的图象.6、有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:)分别为,,,且,三种颜色涂料的粉刷费用(单位:元/)分别为,,,且.在不同的方案中,最低的总费用(单位:元)是()A.B.C.D.【答案】B考点:1.不等式性质;2.不等式比较大小.7、如图,斜线段与平面所成的角为,为斜足,平面上的动点满足,则点的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支【答案】C【解析】试题分析:由题可知,当P点运动时,在空间中,满足条件的AP绕AB旋转形成一个圆锥,用一个与圆锥高成角的平面截圆锥,所得图形为椭圆.故选C.考点:1.圆锥曲线的定义;2.线面位置关系.8、设实数,,满足()A.若确定,则唯一确定B.若确定,则唯一确定C.若确定,则唯一确定D.若确定,则唯一确定【答案】B【解析】试题解析:因为,所以,所以,故当确定时,确定,所以唯一确定.故选B.考点:函数概念二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9、计算:,.【答案】考点:对数运算10、已知是等差数列,公差不为零.若,,成等比数列,且,则,.【答案】【解析】试题分析:由题可得,,故有,又因为,即,所以.考点:1.等差数列的定义和通项公式;2.等比中项.11、函数的最小正周期是,最小值是.【答案】【解析】试题分析:,所以;.考点:1.三角函数的图象与性质;2.三角恒等变换.12、已知函数,则,的最小值是.【答案】考点:1.分段函数求值;2.分段函数求最值.13、已知,是平面单位向量,且.若平面向量满足,则.【答案】【解析】试题分析:由题可知,不妨,,设,则,,所以,所以.考点:1.平面向量数量积运算;2.向量的模.14、已知实数,满足,则的最大值是.【答案】15【解析】试题分析:由图可知当时,满足的是如图的劣弧,则在点处取得最大值5;当时,满足的是如图的优弧,则与该优弧相切时取得最大值,故,所以15z=,故该目标函数的最大值为15.考点:1.简单的线性规划;15、椭圆22221x ya b+=(0a b>>)的右焦点()F,0c关于直线by xc=的对称点Q在椭圆上,则椭圆的离心率是.【答案】2 2考点:1.点关于直线对称;2.椭圆的离心率.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 16. (本题满分14分)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan(A)24π+=.(1)求2sin 2sin 2cos AA A的值; (2)若B ,34a π==,求ABC ∆的面积. 【答案】(1)25;(2)9考点:1.同角三角函数基本关系式;2.正弦定理;3.三角形面积公式.17. (本题满分15分)已知数列n a 和n b 满足,*1112,1,2(n N ),n n a b a a +===∈*12311111(n N )23n n b b b b b n+++++=-∈. (1)求n a 与n b ;(2)记数列n n a b 的前n 项和为n T ,求n T . 【答案】(1)2;nn n a b n ==;(2)1*(1)22()n n T n n N +=-+∈【解析】试题分析:(1)根据数列递推关系式,确定数列的特点,得到数列的通项公式;(2)根据(1)问得到新的数列的通项公式,利用错位相减法进行数列求和.考点:1.等差等比数列的通项公式;2.数列的递推关系式;3.错位相减法求和. 18.(本题满分15分)如图,在三棱锥111ABCA B C 中,011ABC=90=AC 2,AA 4,A ,AB 在底面ABC 的射影为BC 的中点,D 为11B C 的中点.(1)证明: 11D A BC A ⊥平面; (2)求直线1A B 和平面11B C B C 所成的角的正弦值.【答案】(1)略;(2)7(2)作1A F DE ⊥,垂足为F ,连结BF.因为AE ⊥平面1A BC ,所以1BC A E ⊥. 因为BC AE ⊥,所以BC ⊥平面1AA DE . 所以11,BC A F A F ⊥⊥平面11BB C C .所以1A BF ∠为直线1A B 与平面11BB C C 所成角的平面角. 由2,90AB AC CAB ==∠=,得2EA EB ==. 由AE ⊥平面1A BC ,得1114,14A A A B A E ===. 由1114,2,90DE BB DA EA DA E ====∠=,得172A F =. 所以17sin A BF ∠=考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角. 19. (本题满分15分)如图,已知抛物线211C 4x :y=,圆222C (y 1)1x :,过点P(t,0)(t>0)作不过原点O 的直线PA ,PB 分别与抛物线1C 和圆2C 相切,A ,B 为切点.(1)求点A ,B 的坐标; (2)求PAB ∆的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公共点为切点.【答案】(1)222222(2,),(,)11t tA t t Bt t++;(2)32t因为直线PA与抛物线相切,所以216160k kt∆=-=,解得k t=.所以2x t=,即点2(2,)A t t.设圆2C的圆心为(0,1)D,点B的坐标为00(,)x y,由题意知,点B,O关于直线PD对称,故有0000122y xtx t y⎧=-+⎪⎨⎪-=⎩,解得2002222,11t tx yt t==++.即点22222(,)11t tBt t++.(2)由(1)知,21AP t=+直线AP的方程为20tx y t--=,所以点B到直线PA的距离为221dt=+.所以PAB∆的面积为3122tS AP d=⋅=.考点:1.抛物线的几何性质;2.直线与圆的位置关系;3.直线与抛物线的位置关系.20. (本题满分15分)设函数2(),(,)f x x ax b a b R=++∈.(1)当214ab时,求函数()f x在[1,1]上的最小值()g a的表达式;(2)已知函数()f x在[1,1]上存在零点,021b a≤-≤,求b的取值范围. 【答案】(1)222,2,4()1,22,2,24aa ag a aaa a⎧++≤-⎪⎪⎪=-<≤⎨⎪⎪-+>⎪⎩;(2)[3,945]--高考资源网()您身边的高考专家 版权所有@高考资源网- 1 -考点:1.函数的单调性与最值;2.分段函数;3.不等式性质;4.分类讨论思想.。
2015年浙江省高考数学试卷(文科)一、选择题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合P={x|x2﹣2x≥3},Q={x|2<x<4},则P∩Q=()A.[3,4) B.(2,3]C.(﹣1,2)D.(﹣1,3]2.(5分)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.D.3.(5分)设a,b是实数,则“a+b>0”是“ab>0”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.(5分)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β,()A.若l⊥β,则α⊥βB.若α⊥β,则l⊥m C.若l∥β,则α∥βD.若α∥β,则l∥m5.(5分)函数f(x)=﹣(x﹣)cosx(﹣π≤x≤π且x≠0)的图象可能为()A.B.C.D.6.(5分)有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b <c.在不同的方案中,最低的总费用(单位:元)是()A.ax+by+cz B.az+by+cx C.ay+bz+cx D.ay+bx+cz7.(5分)如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支8.(5分)设实数a,b,t满足|a+1|=|sinb|=t.则()A.若t确定,则b2唯一确定B.若t确定,则a2+2a唯一确定C.若t确定,则sin唯一确定D.若t确定,则a2+a唯一确定二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)9.(6分)计算:log2=,2=.10.(6分)已知{a n}是等差数列,公差d不为零,若a2,a3,a7成等比数列,且2a1+a2=1,则a1=,d=.11.(6分)函数f(x)=sin2x+sinxcosx+1的最小正周期是,最小值是.12.(6分)已知函数f(x)=,则f(f(﹣2))=,f(x)的最小值是.13.(4分)已知1,2是平面单位向量,且1•2=,若平面向量满足•1=•=1,则||=.14.(4分)已知实数x,y满足x2+y2≤1,则|2x+y﹣4|+|6﹣x﹣3y|的最大值是.15.(4分)椭圆+=1(a>b>0)的右焦点F(c,0)关于直线y=x的对称点Q在椭圆上,则椭圆的离心率是.三、解答题:本大题共5小题,共74分。
2015年浙江省高考数学试卷(文科)参考答案与试题解析一、选择题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)(2015•浙江)已知集合P={x|x2﹣2x≥3},Q={x|2<x<4},则P∩Q=()A.[3,4)B.(2,3]C.(﹣1,2)D.(﹣1,3]考点:交集及其运算.专题:集合.分析:求出集合P,然后求解交集即可.解答:解:集合P={x|x2﹣2x≥3}={x|x≤﹣1或x≥3},Q={x|2<x<4},则P∩Q={x|3≤x<4}=[3,4).故选:A.点评:本题考查二次不等式的解法,集合的交集的求法,考查计算能力.2.(5分)(2015•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.D.考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:判断几何体的形状,利用三视图的数据,求几何体的体积即可.解答:解:由三视图可知几何体是下部为棱长为2的正方体,上部是底面为边长2的正方形奥为2的正四棱锥,所求几何体的体积为:23+×2×2×2=.故选:C.点评:本题考查三视图与直观图的关系的判断,几何体的体积的求法,考查计算能力.3.(5分)(2015•浙江)设a,b是实数,则“a+b>0”是“ab>0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:利用特例集合充要条件的判断方法,判断正确选项即可.解答:解:a,b是实数,如果a=﹣1,b=2则“a+b>0”,则“ab>0”不成立.如果a=﹣1,b=﹣2,ab>0,但是a+b>0不成立,所以设a,b是实数,则“a+b>0”是“ab>0”的既不充分也不必要条件.故选:D.点评:本题考查充要条件的判断与应用,基本知识的考查.4.(5分)(2015•浙江)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β,()A.若l⊥β,则α⊥βB.若α⊥β,则l⊥m C.若l∥β,则α∥βD.若α∥β,则l∥m考点:空间中直线与平面之间的位置关系.专题:综合题;空间位置关系与距离.分析:A根据线面垂直的判定定理得出A正确;B根据面面垂直的性质判断B错误;C根据面面平行的判断定理得出C错误;D根据面面平行的性质判断D错误.解答:解:对于A,∵l⊥β,且l⊂α,根据线面垂直的判定定理,得α⊥β,∴A正确;对于B,当α⊥β,l⊂α,m⊂β时,l与m可能平行,也可能垂直,∴B错误;对于C,当l∥β,且l⊂α时,α与β可能平行,也可能相交,∴C错误;对于D,当α∥β,且l⊂α,m⊂β时,l与m可能平行,也可能异面,∴D错误.故选:A.点评:本题考查了空间中的平行与垂直关系的应用问题,也考查了数学符号语言的应用问题,是基础题目.5.(5分)(2015•浙江)函数f(x)=(x ﹣)cosx(﹣π≤x≤π且x≠0)的图象可能为()A.B.C.D.考点:函数的图象.专题:函数的性质及应用.分析:由条件可得函数f(x)为奇函数,故它的图象关于原点对称;再根据在(0,1)上,f(x)<0,结合所给的选项,得出结论.解答:解:对于函数f(x)=(x﹣)cosx(﹣π≤x≤π且x≠0),由于它的定义域关于原点对称,且满足f(﹣x)=(﹣x)cosx=﹣f(x),故函数f(x)为奇函数,故它的图象关于原点对称.故排除A、B.再根据在(0,1)上,>x,cosx>0,f(x)=(x﹣)cosx<0,故排除C,故选:D.点评:本题主要考查函数的奇偶性的判断,奇函数的图象特征,函数的定义域和值域,属于中档题.6.(5分)(2015•浙江)有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y <z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是()A.a x+by+cz B.a z+by+cx C.a y+bz+cx D.a y+bx+cz考点:函数的最值及其几何意义.专题:函数的性质及应用.分析:作差法逐个选项比较大小可得.解答:解:∵x<y<z且a<b<c,∴ax+by+cz﹣(az+by+cx)=a(x﹣z)+c(z﹣x)=(x﹣z)(a﹣c)>0,∴ax+by+cz>az+by+cx;同理ay+bz+cx﹣(ay+bx+cz)=b(z﹣x)+c(x﹣z)=(z﹣x)(b﹣c)<0,∴ay+bz+cx<ay+bx+cz;同理az+by+cx﹣(ay+bz+cx)=a(z﹣y)+b(y﹣z)=(z﹣y)(a﹣b)<0,∴az+by+cx<ay+bz+cx,∴最低费用为az+by+cx故选:B点评:本题考查函数的最值,涉及作差法比较不等式的大小,属中档题.7.(5分)(2015•浙江)如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支考点:圆锥曲线的轨迹问题.专题:圆锥曲线的定义、性质与方程.分析:根据题意,∠PAB=30°为定值,可得点P的轨迹为一以AB为轴线的圆锥侧面与平面α的交线,则答案可求.解答:解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.此题中平面α上的动点P满足∠PAB=30°,可理解为P在以AB为轴的圆锥的侧面上,再由斜线段AB与平面α所成的角为60°,可知P的轨迹符合圆锥曲线中椭圆定义.故可知动点P的轨迹是椭圆.故选:C.点评:本题考查椭圆的定义,考查学生分析解决问题的能力,比较基础.8.(5分)(2015•浙江)设实数a,b,t满足|a+1|=|sinb|=t.()A.若t确定,则b2唯一确定B.若t确定,则a2+2a唯一确定D.若t确定,则a2+a唯一确定C.若t确定,则sin唯一确定考点:四种命题.专题:开放型;简易逻辑.分析:根据代数式得出a2+2a=t2﹣1,sin2b=t2,运用条件,结合三角函数可判断答案.解答:解:∵实数a,b,t满足|a+1|=t,∴(a+1)2=t2,a2+2a=t2﹣1,t确定,则t2﹣1为定值.sin2b=t2,A,C不正确,∴若t确定,则a2+2a唯一确定,故选:B点评:本题考查了命题的判断真假,属于容易题,关键是得出a2+2a=t2﹣1,即可判断.二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)9.(6分)(2015•浙江)计算:log2=,2=.考点:对数的运算性质.专题:函数的性质及应用.分析:直接利用对数运算法则化简求值即可.解答:解:log2=log2=﹣;2===3.故答案为:;.点评:本题考查导数的运算法则的应用,基本知识的考查.10.(6分)(2015•浙江)已知{a n}是等差数列,公差d不为零,若a2,a3,a7成等比数列,且2a1+a2=1,则a1=,d=﹣1.考点:等比数列的性质.专题:等差数列与等比数列.分析:运用等比数列的性质,结合等差数列的通项公式,计算可得d=﹣a1,再由条件2a1+a2=1,运用等差数列的通项公式计算即可得到首项和公差.解答:解:由a2,a3,a7成等比数列,则a32=a2a7,即有(a1+2d)2=(a1+d)(a1+6d),即2d2+3a1d=0,由公差d不为零,则d=﹣a1,又2a1+a2=1,即有2a1+a1+d=1,即3a1﹣a1=1,解得a1=,d=﹣1.故答案为:,﹣1.点评:本题考查等差数列首项和公差的求法,是基础题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.11.(6分)(2015•浙江)函数f(x)=sin2x+sinxcosx+1的最小正周期是π,最小值是.考点:二倍角的余弦;三角函数的最值.专题:三角函数的图像与性质.分析:由三角函数恒等变换化简解析式可得f(x)=sin(2x﹣)+,由正弦函数的图象和性质即可求得最小正周期,最小值.解答:解:∵f(x)=sin2x+sinxcosx+1=+sin2x+1=sin(2x﹣)+.∴最小正周期T=,最小值为:.故答案为:π,.点评:本题主要考查了三角函数恒等变换的应用,考查了正弦函数的图象和性质,属于基本知识的考查.12.(6分)(2015•浙江)已知函数f(x)=,则f(f(﹣2))=,f(x)的最小值是2﹣6.考点:函数的最值及其几何意义.专题:函数的性质及应用.分析:由分段函数的特点易得f(f(﹣2))=的值;分别由二次函数和基本不等式可得各段的最小值,比较可得.解答:解:由题意可得f(﹣2)=(﹣2)2=4,∴f(f(﹣2))=f(4)=4+﹣6=﹣;∵当x≤1时,f(x)=x2,由二次函数可知当x=0时,函数取最小值0;当x>1时,f(x)=x+﹣6,由基本不等式可得f(x)=x+﹣6≥2﹣6=2﹣6,当且仅当x=即x=时取到等号,即此时函数取最小值2﹣6;∵2﹣6<0,∴f(x)的最小值为2﹣6故答案为:﹣;2﹣6点评:本题考查函数的最值,涉及二次函数的性质和基本不等式,属中档题.13.(4分)(2015•浙江)已知1,2是平面向量,且1•2=,若平衡向量满足•1=•=1,则||=.考点:平面向量数量积的性质及其运算律.专题:平面向量及应用.分析:根据数量积得出1,2夹角为60°,<,1>=<,2>=30°,运用数量积的定义判断求解即可.解答:解:∵1,2是平面单位向量,且1•2=,∴1,2夹角为60°,∵平衡向量满足•1=•=1∴与1,2夹角相等,且为锐角,∴应该在1,2夹角的平分线上,即<,1>=<,2>=30°,||×1×cos30°=1,∴||=故答案为:点评:本题简单的考查了平面向量的运算,数量积的定义,几何图形的运用,属于容易题,关键是判断夹角即可.14.(4分)(2015•浙江)已知实数x,y满足x2+y2≤1,则|2x+y﹣4|+|6﹣x﹣3y|的最大值是15.考点:简单线性规划.专题:开放型;不等式的解法及应用.分析:由题意可得2x+y﹣4<0,6﹣x﹣3y>0,去绝对值后得到目标函数z=﹣3x﹣4y+10,然后结合圆心到直线的距离求得|2x+y﹣4|+|6﹣x﹣3y|的最大值.解答:解:如图,由x2+y2≤1,可得2x+y﹣4<0,6﹣x﹣3y>0,则|2x+y﹣4|+|6﹣x﹣3y|=﹣2x﹣y+4+6﹣x﹣3y=﹣3x﹣4y+10,令z=﹣3x﹣4y+10,得,如图,要使z=﹣3x﹣4y+10最大,则直线在y轴上的截距最小,由z=﹣3x﹣4y+10,得3x+4y+z﹣10=0.则,即z=15或z=5.由题意可得z的最大值为15.故答案为:15.点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.15.(4分)(2015•浙江)椭圆+=1(a>b>0)的右焦点F(c,0)关于直线y=x的对称点Q在椭圆上,则椭圆的离心率是.考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.解答:解:设Q(m,n),由题意可得,由①②可得:m=,n=,代入③可得:,解得e2(4e4﹣4e2+1)+4e2=1,可得,4e6+e2﹣1=0.即4e6﹣2e4+2e4﹣e2+2e2﹣1=0,可得(2e2﹣1)(2e4+e2+1)=0解得e=.故答案为:.点评:本题考查椭圆的方程简单性质的应用,考查对称知识以及计算能力.三、解答题:本大题共5小题,共74分。