平面波传播的传输线模型

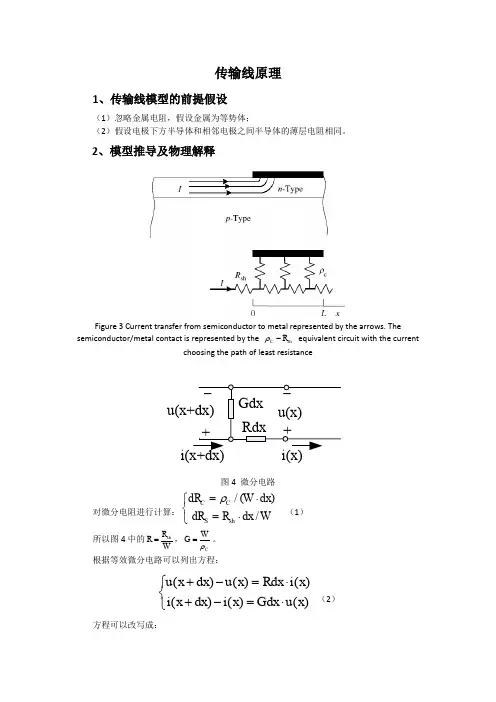
传输线原理1、传输线模型的前提假设（1）忽略金属电阻，假设金属为等势体；（2）假设电极下方半导体和相邻电极之间半导体的薄层电阻相同。

2、模型推导及物理解释Figure 3 Current transfer from semiconductor to metal represented by the arrows. Thesemiconductor/metal contact is represented by the C sh R ρ- equivalent circuit with the currentchoosing the path of least resistance图4 微分电路对微分电阻进行计算：/()/C C S sh dR W dx dR R dx Wρ=⋅⎧⎨=⋅⎩ （1）所以图4中的sh R R W=，C W G ρ=。

根据等效微分电路可以列出方程：()()()()()()u x dx u x Rdx i x i x dx i x Gdx u x +-=⋅⎧⎨+-=⋅⎩ （2） 方程可以改写成：()()()()du x Ri x dxdi x Gv x dx⎧=⎪⎪⎨⎪=⎪⎩ （3） 写成二阶常微分方程的形式：222222()()0()()0d u x u x dx d i x i x dx αα⎧-=⎪⎪⎨⎪-=⎪⎩ （4） 该常微分方程组的通解形式为：12120()()x x x x u x A e A e A e A e i x Z αααα--⎧=+⎪-⎨=⎪⎩（5）其中，0Z ==1、当给定边界条件0x =处电压、电流分别为1U 、1I 时，代入通解中求出系数得出最终解（部分文献给出这样的形式）：11011011011000()22()22x x x x U I Z U I Z u x e e U I Z U I Z i x e e Z Z αααα--+⋅-⋅⎧=+⎪⎪⎨+⋅-⋅⎪=-⎪⎩（6） 将解的形式改写成双曲函数的形式：110110()cosh sinh ()cosh sinh u x U x I Z x U i x I x x Z αααα=+⋅⎧⎪⎨=+⎪⎩（7）2、如果给定边界条件0x =处电流为(0)0i =，x L =处电流为()i L I =，可以求得系数为0122sinh I Z A A Lα⋅==，最终解为（部分文献给出这样的形式）：0()cosh sinh I Z u x x Lαα⋅= （8）由于图4中的x 坐标定在接触电极的右端，改成接触电极的左端，上述方程应该变成：()cosh ()sinh I Z u x L x Lαα⋅=- （9）电压曲线在图5中画出，可以看出当电流从半导体流入金属时，接触电极下方的电压随着x 轴的方向而衰减，当电压衰减到1/e 时的位置称为电流的扩散长度，有1T L α==扩散长度可以看成电流从半导体流入金属时，在电极下方大部分电流扩散的距离。

Reflect反射是引起SI的一个最基本因素，信号在传输线传播过程中，一旦它所感受到的传输线瞬时阻抗发生变化，那么就必将有发射发生。

反射是由于传输线瞬时阻抗变化而引起的下面就从理论角度来分析一下反射的机理、反射系数和传输系数的计算配个简易图来加以说明图中褐色的为电路板上的大面积铺铜层（GND或者PWR），它是信号的返回路径。

绿色和红色是传输线，S1比较宽，S2较窄，很明显在S1和S2的交接处出现了阻抗不连续，根据阻抗计算公式应该是Rs1<Rs2。

那么信号传输到这里的时候，从反射的定义来看应该是发生了反射。

那么究竟有多少信号被反射了呢？又有多少信号通过了界面进入S2了呢？这里就涉及到了反射的计算，即反射系数的计算和传输系数的计算在交界面，虽然阻抗发生了变化，但是电压和电流一定都是连续的这个结论一定要能理解，电压和电流不可能出现一个断裂即在交界面的左边一点和右边一点，他们的电压和电流都是相等的这里的一点点就像微积分中的那么一小点在分界面的左边一点点S1中有：Rs1=V1/I1（1）在分界面的右边一点点S2中有：Rs2=V2/I2（2）其中的V1、V2分别为分界面两侧的电压，I1和I2为分界面两侧的电压由上面的电压和电流连续性得知：V1=V2,I1=I2（3）分析上面的三组方程，如果没有反射，他们是不可能同时成立的因为Rs1和Rs2是不相等的所以可以判定在分界面必定存在反射回源端的信号反射电压设为Vf，反射电流为If进入S2的电压为Vt，电流为It（称他们为传输电压和传输电流）信号电压为Vi，电流为Ii（称之为输入电压，从分界面看）电压关系有：Vi+Vf=Vt电流关系有：Ii-If=It这又是很关键的两个关系式因为Vi/Ii=Rs1Vf/If=Rs1Vt/It=Rs2把这三个关系式代入到上面的两个电压和电流关系方程中可以得到Vi/Rs1-Vf/Rs1=Vt/Rs2=（Vi+Vf）/Rs2（Vi-Vf）/Rs1=（Vi+Vf）/Rs2反射系数X定义为反射电压和输入电压的比值，即Vf/Vi可求的X=（Rs2-Rs1）/（Rs1+Rs2）传输系数Y定义为传输电压和输入电压的比值，即Vt/Vi经过X式小变形即可求得可求的Y=2Rs2/（Rs1+Rs2）反射是经常遇到的SI问题，我们只能无限地缩小它，却不能完全消除它，在波形能够接受的情况下尽量做到最大限度的抑制反射，这就是我们要做的工作。